基于Markov切换模型的采购经理指数波动特征研究

王路加 郭亚妮

一、引 言

伴随着经济总量持续增大，物价波动愈加剧烈和频繁，中国政府决策游移于扩张性与紧缩性的宏观政策之间，试图在保障我国经济平稳增长的同时最大化的稳定通货膨胀，进而促使社会有序发展。采购经理人指数（简称PMI指数）反映制造业总体经济走势的变化情况，对预测和调控宏观经济具有重要的意义，也是中国经济学界亟待解决的现实问题。

采购经理人指数（PMI）作为全球关注的经济先行指数，在各国都引起高度重视，是研究各国宏观经济的重要参考指标。与此同时，国内学者也对中国市场PMI指数进行了深入研究。孙燕红研究PMI指数与GDP指数之间相互关系，用以中国经济增长的预测，结果表明，PMI指数对预判中国经济景气程度具有一定的参考价值。此外，桂文林等通过构建EEMD-JADE模型，对中国市场的PMI指数与PPI指数结构视角下的分化走势进行了研究。他们指出，PMI和PPI可以重构出三个结构分量，即高中低频分别反映短期波动、中期波动和长期波动。

国内学者一直使用马尔科夫切换模型作为研究股票获利率、股市波动率的工具，国外学者通过Markov切换模型研究居民消费价格指数进而帮助国家对宏观经济的调控。国内学者多使用非线性时间序列预测模型研究采购经理人指数的波动特征，而这些研究无法描述采购经理人指数时间序列下的复杂变化特征，马尔科夫切换模型适用于采购经理人指数波动的复杂变化。本文通过使用马尔科夫切换模型对中国采购经理人指数进行实证分析，检验了采购经理人指数波动率的持续性、波动幅度及波动频率等特征，从而为监管部门对国家宏观经济调控提供了一定参考。

二、Markov切换模型

（一）模型建立

Markov切换模型是利用给定指标序列的历史数据来对当前和未来进行拟合和预测，体现了不同时期波动率之间的相关性和滞后性。论文对一般的Markov切换模型进行动态化，以便于更好的拟合数据信息，即将公式（1）变为公式（2）：

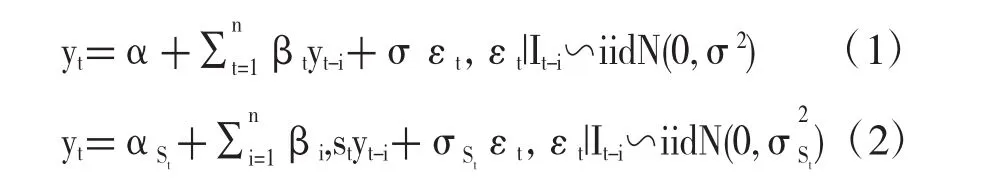
公式（2）中，St表示t时刻因变量所处的机制状态，一般是事先设定的，如果存在k个机制，那么St=1,2…k，并且当St的变化满足k个机制的一阶Markov链时，St的转移概率为 Pij=Pr（St+1=j|St=i），∑Pij＝1，∀i,j∈{1,2,…,k}，机制之间的转移概率可以通过转移矩阵P来表示（如式（3）所示）；αSt为模型在St机制状态下的常数项；n为模型中包含的自回归滞后项的最大阶数；βi,St为模型在St机制状态下的i阶滞后项的自回归系数；γt-i表示因变量的i阶滞后项，αSt为模型在St机制状态下的标准差；εt为模型的残差项，通常假定该残差项服从均值为0，方差为的正态分布。需要注意的是，这里的方差不是固定的，而是随着模型机制状态St的变化而变化。

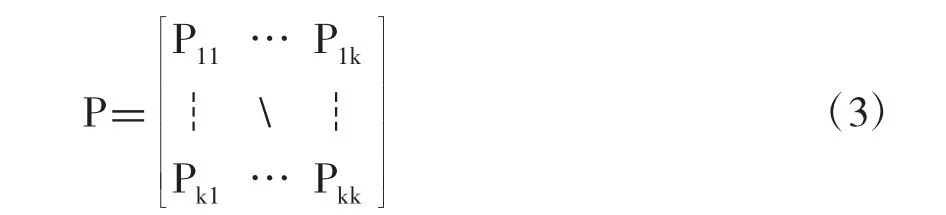
此外，在式（2）所示的Markov切换模型基础上，如果加入外生变量，那么式（2）所示的Markov切换模型形式可变为式（4）所示的模型结果，其中m表示外生变量的个数，βi,s,为模型在St机制状态下的第j个外生变量的回归系数。

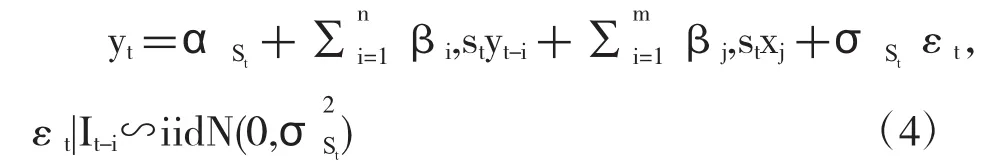
由式（4）不难发现，Markov切换模型可以根据模型的截距、均值、变量系数和残差项方差将模型结构分为一般的Markov切换模型、含滞后项的Markov切换模型以及含外生变量的Markov切换模型。

（二）模型的估计方法

Markov切换模型的估计方法主要使用极大似然估计方法和蒙特卡洛模拟方法。对于某个给定时刻t的随机变量yt的极大似然函数是由每个机制下的概率密度函数通过处于该机制的概率进行加权求和得到：

设总观察时期为T，结合每个时期的似然函数，相乘并取对数，转化为每个时期的对数似然函数进行加总求和。完整的似然函数表示如下：

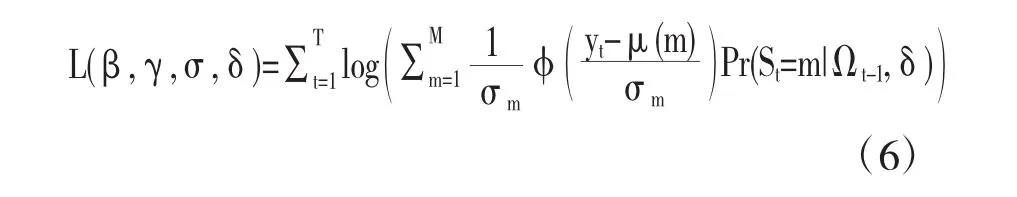
式（6）中，条件概率是以一种抽象的形式，应设法把条件概率P表示成待估参数的函数，才可以通过数值优化求得最大似然函数值。简单的转移模型中，可以假设条件概率是服从一系列可观测变量Gt-1的多元logit模型，其中Gt-1的系数为δ。

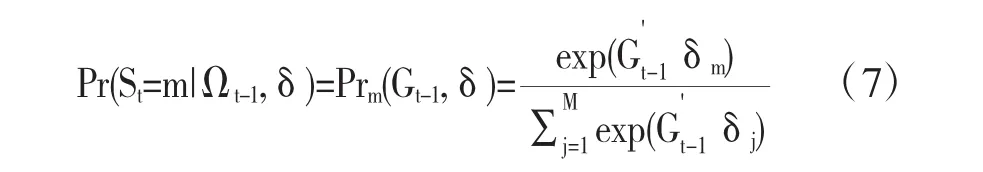
结合式（6）和式（7），可以得到似然函数转化为

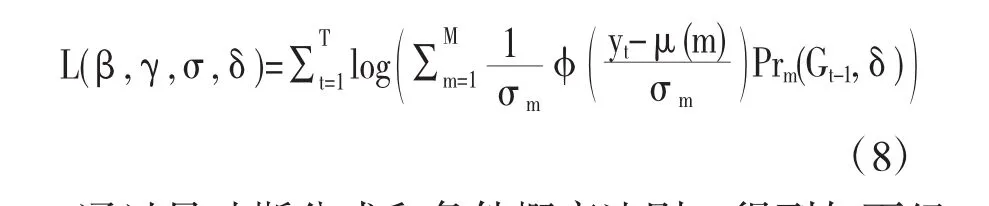
通过贝叶斯公式和条件概率法则，得到如下经过过滤的表达式：

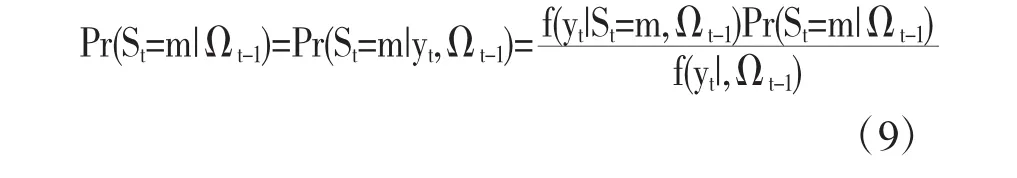
式（9）右边的部分通过概率密度函数进行替换得到

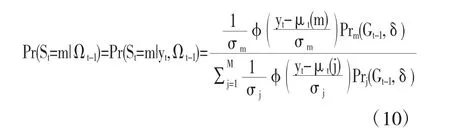
上述过程重复迭代直到零期，便可以得到待估参数和初始概率表示的极大似然函数表达式，使似然函数取最大值，便得到相应的参数值及初始变量。具体可以通过以下4个步骤加以说明：

第1步：通过Markov切换模型矩阵和基本的概率规则，得到t时期处于机制m的条件概率。利用条件概率公式反复迭代，以此类推，该条件概率可以表示为初始概率和转移概率的表达式：Pr(St=m|Ωt-1)=

第2步：在假设模型残差项服从正态分布的情况下，可以得到t时期处于机制m的概率密度表达式：

第3步：通过加总t时期m个机制的概率密度，可以进一步得到 t时期的似然函数：Lt(β,γ,σ,δ)=

第4步：更新上述式子中的条件概率，得到过滤概率，如下。如果总观察时期为T，那么结合每个时期的似然函数，相乘并取对数，转化为每个时期的对数似然函数进行加总求和，便可以得到完整的似然函数

三、PMI指数波动特征的实证分析

（一）数据的选取

本文选取PMI指数作为研究对象，通过Markov切换模型分析PMI的内在特征。数据时段为2005年1月至2015年12月的月度数据（http://www.edatasea.com/）。以月增长率对数时间序列Yi,t=100ln（PMIi,t/PMIi,t-1）构成样本空间，这里定义为PMI_T。模型均采用Eviews8.0操作。

（二）基本统计特征分析

图 1（a）和图 1（b）描述了 PMI指数以及月增长率对数序列（定义为PMI指数时间序列）的时间路径情况。首先，从波动幅度来看，论文可以观察到PMI时间序列的波动逐渐趋于稳定（如图1（b）所示）。其次，PMI时间序列存在明显的“聚集波动”现象，即在某一段时间内波动率普遍偏大，而在另一段时间内波动率普遍偏小（如图1（b）所示）。最后，从PMI指数的历史路径来看，整体呈现下滑趋势，并且在2008年-2009年之间伴随一次大的变化，这可能源自于2008金融危机的影响。

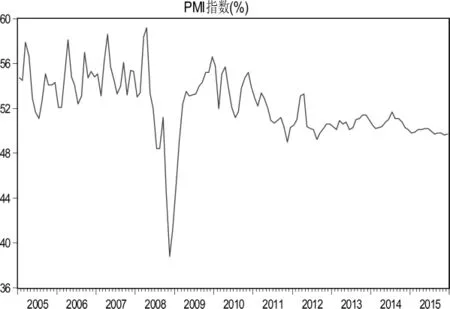
图1 （a） PMI指数的时间途径图

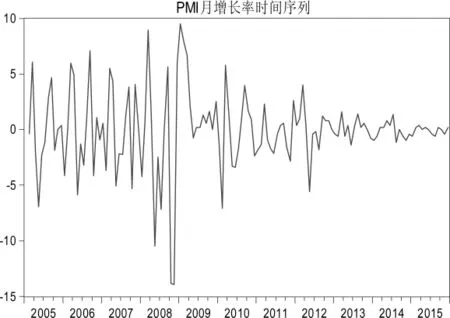
图1 （b） PMI指数时间序列的时间途径图

为了验证上述基本情况的可靠性，论文以PMI时间序列为对象进一步分析波动特征。在此之前，为了确认月增长率序列是否存在单位根（检验波动是否平稳），论文采用单位根检验（ADF），滞后项的确定采用SIC（Schwarz Info Criterion）准则。结果如表1（a）所示，PMI时间序列在1%的显著性水平下显著，说明月增长率序列不存在单位根，即PMI时间序列的波动率是平稳的。

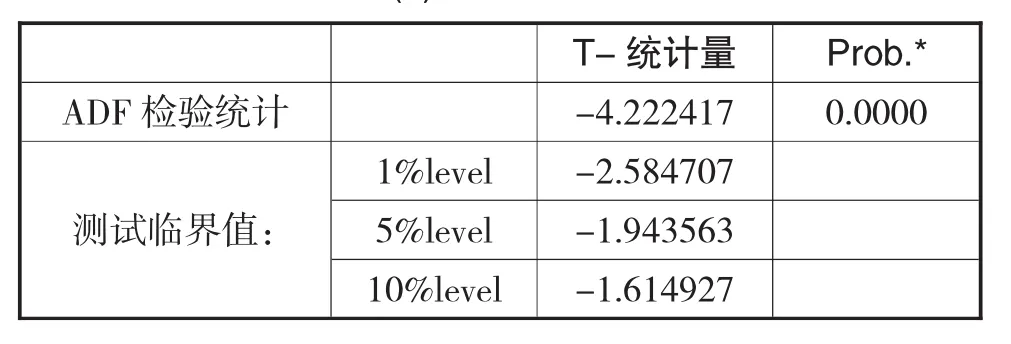
表1 (a) 单位根检验

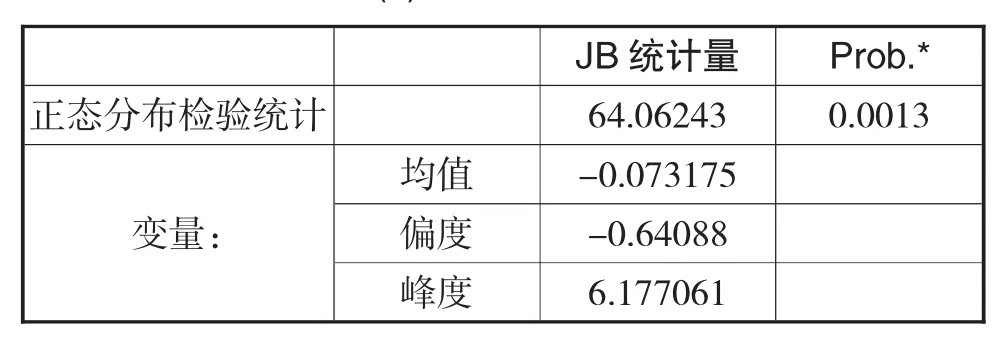
表2 (b) 正态分布检验

进一步分析PMI时间序列是否服从标准正态分布，结果如表 1（b）所示，偏度系数（-0.64088）小于零，说明同时期PMI指数的月增长率大于平均增长率的情况居多，并根据偏度不等于零，说明在2005年至2015年间PMI指数的月增长率的分布具有非对称特征。峰度系数（6.177061）大于3，说明该分布呈现高峰厚尾的特征，并具有多个的极端值。JB统计量为64.06243，说明变量逐渐偏离正态分布。

（三）PMI时间序列对数序列机制转变的检验

目前已经检验PMI时间序列存在平稳性，并且不服从正态分布，如果能够检验到PMI时间序列发生机制转变或状态转变，就可以说明PMI时间序列存在结构变点的波动特征。对机制转变或状态转变的检验最初来自于模型参数稳定性的检验：如果在样本期内PMI时间序列没有发生机制转变，那么说明在样本期内的模型参数保持不变；如果在样本期内PMI时间序列发生机制转变，那么说明在样本期内的模型参数具有结构变化。这里对应的检验方法有 Chow检验、Bai-Perron检验、CUSUM检验、La-grange Multiplikator检验、Likelihood Ratio检验等。论文主要通过CUSUM方法来检验PMI时间序列是否存在结构变点特征。

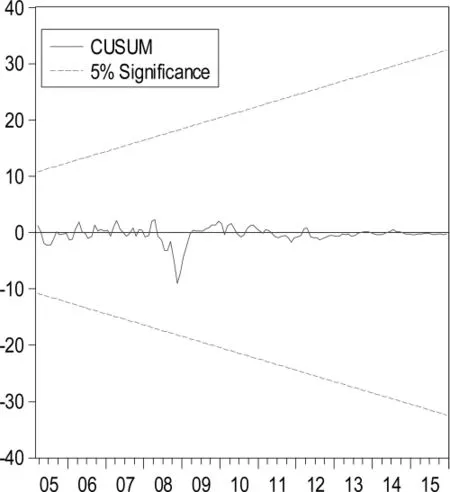
图2 （a） 无滞后项的CUSUM检验

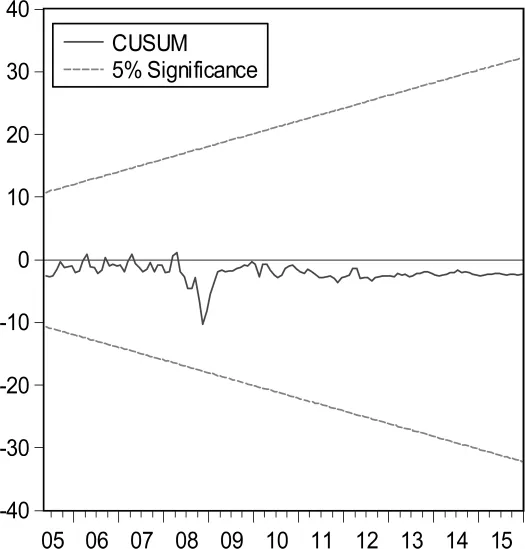
图2 （b） 滞后一阶的CUSUM检验

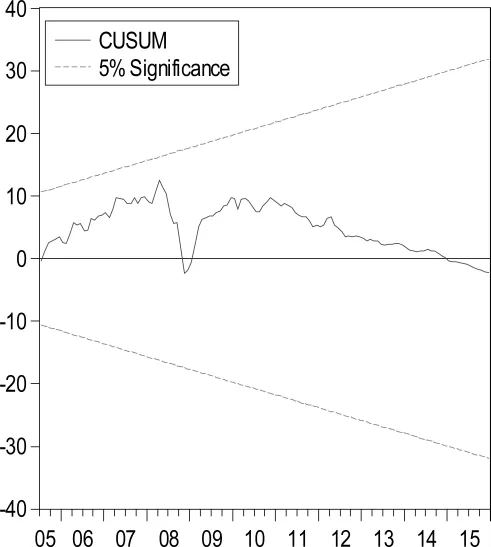
图2 （c） 滞后二阶的CUSUM检验

从图2（a）可以看出，CUSUM实线所表示的统计量从2005年之后均没有超出了虚线范围，说明在5%的显著性下，PMI时间序列在无滞后情况下没有显著的结构性变点现象。同理，从图2（b）和图2（c）可以看出，CUSUM实线所表示的统计量从2005年之后均没有超出了虚线范围，说明在5%的显著性下，PMI时间序列在滞后一阶和滞后二阶情况下依旧不存在结构性变点现象。所以得到，PMI时间序列没有发生结构变点的波动现象。

（四）Markov切换模型的实证分析

考虑到三个形态机制的模型对波动过程更细致的划分，可以有效避免将中等波动状态纳入低波动状态或高波动状态而造成的误差，为此将Markov切换模型划分为三个机制形态。同时根据CUSUM检验对PMI时间序列滞后二阶情况下的结构性变化更大，所以对PMI时间序列的自回归模型采取滞后二阶的切换模型，通过对数极大似然法对参数进行估计，得到表2所示的结果。

进一步给出PMI时间序列的切换模型：

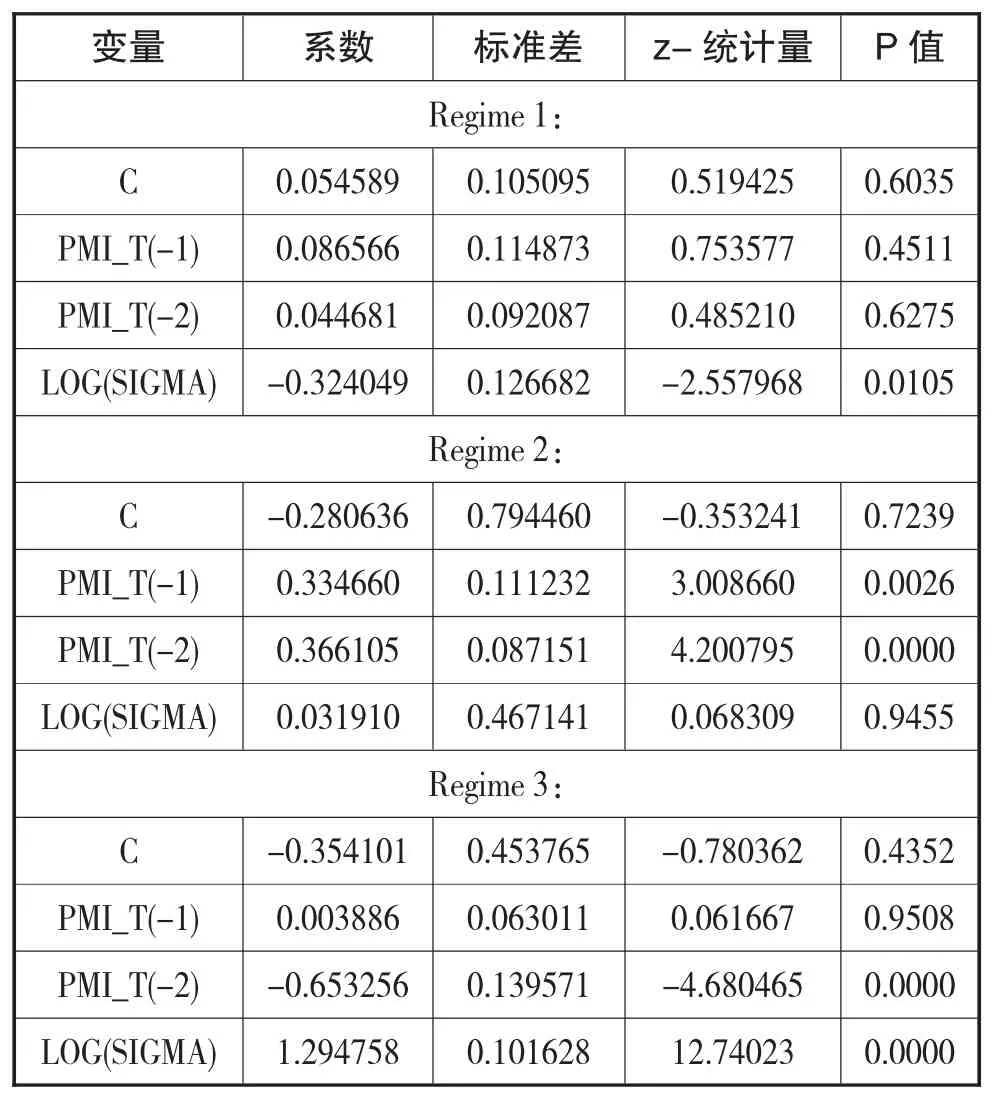
表2 Markov切换模型的参数估计

模型的转移概率矩阵如表3所示：

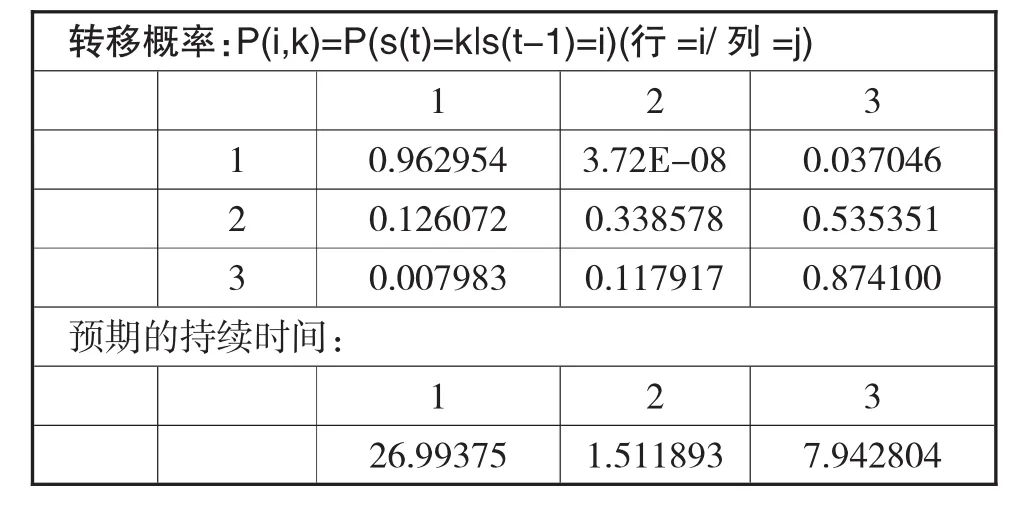
表3 转移概率矩阵

根据式（11）中标准差的大小，论文把三种状态定义为低波动性（σ1=12.668%），中等波动（σ2=46.714%）以及高波动（σ3=10.163%）的三种状态。通过观察每个状态下的自回归方程，论文可以发现PMI时间序列在不同状态之间的变动规律有一定的差异性。当期PMI时间序列同增长率滞后项的相关性随波动状态变化而变化，有强有弱，有正有负。在低波动状态和中等波动状态下，PMI时间序列一阶滞后项和二阶滞后项与当期增长率呈正相关关系；在高波动状态下，PMI时间序列一阶滞后项与当期增长率呈正相关关系，二阶滞后项与当期增长率呈负相关关系，而且二阶滞后项与当期增长率存在较强的相关性。这说明，不同波动状态下PMI时间序列的反应时间不同，信息冲击的滞后效应也各不相同。在转移概率矩阵中（如表3所示），三个状态在下一期保持不变的概率分别为96.2954%、33.8578%和87.41%。由此可知，中波动状态的持续性（长记忆性）最差，而低等波动状态持续性最高，这从本质层面揭示了“波动群集”现象产生的根本原因。另外，根据期望久期的定义，可以得到低、中、高波动区制的持续久期（1-P）-1分别为：26.99个月、1.51个月、7.94个月。按照一年有12个月计算，低波动状态的持续时间约为9个月，高波动状态的持续时间约为3个月。由此可得出，我国的PMI指数波动长期处于低波动状态。

进一步地，从转换概率矩阵可以看出，低波动状态1和中波动状态2向高波动状态3转移的概率较低，而中波动状态2和低波动状态1向高波动状态3转移的概率较高，分别是12.607%和53.535%；同样地，高等波动的状态3向中波动状态2转移的概率也较高，为11.792%。这说明三种状态之间的切换结果主要集中于中波动状态2和高波动状态3，这里可以根据这三种状态的平滑概率图形进一步验证，具体如图3所示。

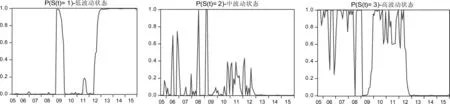
图3 PMI时间序列的低、中、高波动机制的平滑概率图

从图3可以进一步得到，三个不同状态的波动的频率和分段波动特征。按照80%的平滑概率作为划分状态的一个标准，则在2005年到2015年之间处于低波动状态1和高波动状态的概率最多，此期间大部分的时间平滑概率高达90%以上，部分时间点平滑概率甚至达到了100%。同时观察三种波动的平滑概率图进一步发现，2005年至2015年的PMI指数的波动性分成三个阶段：第一阶段，在2008年以前，PMI波动性普遍较大，市场处于高等波动性和中等波动性的交替切换模式，并且中等波动性的状态出现次数较少。第二阶段，2008年至2012年，PMI指数处于三种波动状态的切换模式，特别以2008-2009年的形态最为显著，这可能也是源自于2008年经济危机的影响。第三阶段，2012年之后，PMI波动性处于低波动模式，说明至2012年之后经济发展处于平稳状态，这于实际情况也较为吻合。

四、其他经济体对中国PMI的影响分析

为了更深入了解中国PMI指数是否受到其他国家相关指数的冲击，论文进一步加入美国PMI指数、欧盟PMI指数（以英国、法国、德国、意大利和俄罗斯的平均值计算）和亚太地区PMI指数（以日本、韩国、印度、澳大利亚和新加波的平均值计算）的时间序列数据（http://www.edatasea.com/），通过建立 VAR 自回归模型进而运用脉冲响应函数方法进行分析，从而研究四大经济体之间制造业PMI之间的相互影响关系，具体过程见文献的详细分析，论文重点关注脉冲响应函数，具体结果如图 4（a）和 4（b）所示。

结合图 4（a）和 4（b）可以看出，中国 PMI指数对来自美国PMI指数和自身冲击的最大响应分别为1.5%和2.6%。欧盟PMI指数和日本PMI指数对中国PMI指数的最大冲击也集中于第5期至第10期，由此可见，中国经济体中PMI指数受自身的影响较为显著，其次是主要受美国和亚太地区的影响，同时也说明其他经济体PMI指数到中国PMI指数的传导机制在中国经济体中是存在的。所以，中国PMI指数除了受到自身影响外，还会受到其他经济体的PMI指数的影响，其中以美国PMI指数对中国PMI指数的影响最为显著。

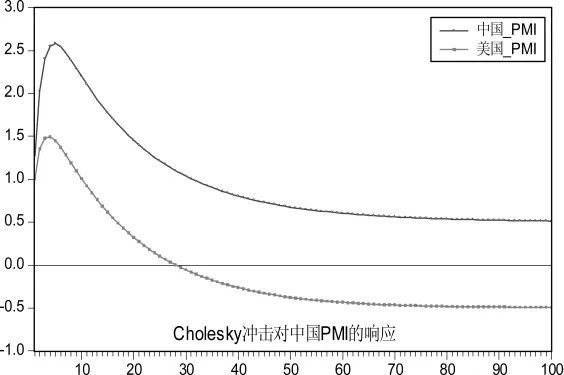
图4 （a）中美PMI对中国PMI冲击响应

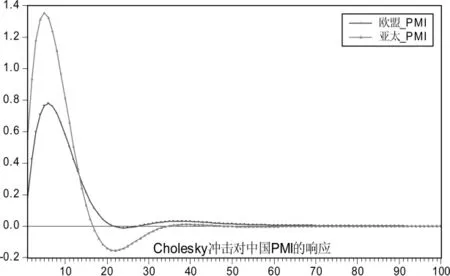
图4 （b） 欧盟、日本PMI对中国PMI冲击响应

结合 Cholesky 冲击响应图 4（a）和图 4（b）说明了其他经济体PMI指数到中国PMI指数的传导机制在中国经济体中存在，因此在观察中国PMI指数变化的过程中也不能忽视其他经济体对中国PMI指数的影响，应合理加入其他经济体的PMI指数，甚至考虑加入其他经济体的PPI指数、CPI指数等所产生的耦合效应。这样才能更精确地描述中国PMI指数的动态特征，在后期预测中国宏观经济发展和变化上才能发挥其应有的价值，特别是在新常态经济背景下更应该重视其他经济体对中国相关价格指数的影响。

五、结 论

论文的创新点在于使用马尔科夫切换模型对采购经理人指数波动特征的复杂表现进行了分析，PMI时间序列存在明显的非对称性波动特征，并且前一期的PMI时间序列的波动会加剧下一期PMI时间序列的波动，PMI指数的波动有显著的滞后效应，存在非对称性的“杠杆效应”。除此之外，论文研究PMI波动性的持续性、波动幅度以及波动频率进一步发现，在高波动状态下，PMI时间序列一阶滞后项与当期增长率呈正相关关系，二阶滞后项与当期增长率呈负相关关系。从波动持续性来看，低波动特征相比其他两种特征持续时间更长，进而导致波动状态的切换主要集中于中波动状态和高波动状态。从波动幅度来看，PMI时间序列的波动主要稳定于低波动率，并且存在明显的“聚集波动”现象。从波动频率来看，在2005年到2015年之间PMI时间序列存在多阶段的分布格局。最后，为了更深入了解中国PMI指数是否受到其他国家相关指数的冲击，进一步加入美国PMI指数、欧盟PMI指数和亚太地区PMI指数的时间序列数据，建立VAR自回归模型，对建立的VAR模型运用脉冲响应函数方法进行分析，从而研究四大经济体之间制造业PMI之间的相互影响关系。结果显示，中国PMI指数除了受到自身影响外，还会受到其他经济体的PMI指数的影响，其中以美国PMI指数对中国PMI指数的影响最为显著。

【参考文献】

［1］ Daniel Bachman.The Information Content of the ISM Purchasing Managers’Survey,http://ssrn.com/abstract=170 2342.2010-8-3

［2］于颖，蔡进.中国PMI（采购经理指数）与其他数据相关性研究. 社会纵横.2008（12）68-70

［3］于颖.中国PMI数据的实际应用-PMI的领先性分析.社会纵横.2009（12）43-35

［4］方力.PMI指数是否是可靠的经济景气指标.华北金融.2012（7）4-21

［5］孟文强，任一鑫.对采购经理人指数的一个分析——基于时间序列和神经网络模型.经济管理.2013（5）149-159

［6］张栋华.中国指数作用和质量的测度.经济统计学.季刊.2014（1）171-184

［7］张栋华.制造业PMI指数追踪经济的作用分析.广东广播电视大学学报.2014.23（5）105-112

［8］孙燕红.PMI及其对中国经济增长预测的研究.安徽.安徽大学.2014

［9］桂文林，黎庆莹.基于EEMD-JADE模型的PMI与PPI结构分析及传导机制.数量经济技术经济研究.2017（4）110-128

［10］冯艳慧.中国股市收益波动的机制特征研究.吉林.吉林大学.2015

［11］Hamilton JD.A New Approach totheEconomic Analysis of Nonstationary Time Series and the Business Cycle.general information.1989.57（2）357-84

［12］Hamilton JD,SusmelR.Autoregressive conditional heteroskedasticity and changes in regime.Journalof Econometrics.1994.64（1）307-333

［13］Penza P.,Bansal V.K..Measuring Market Risk with Value at Risk.John Wiley&Sons.2001

［14］何跃，杨小朋.美国、欧盟、日本和中国制造业PMI之间的相互影响关系.情报杂志.2013（2）186-195