复数单元检测题（B卷）

■河南省南阳市镇平县二高 谭武军

一、选择题

1.i是虚数单位,若集合S={-1,0,1},则( )。

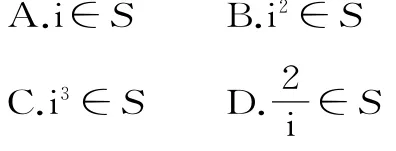
2.a=0是复数a+bi(a,b∈R)为纯虚数的( )。

A.充分不必要条件

B.必要不充分条件

C.充要条件

D.不充分也不必要条件

3.适合x-3i=(8x-y)i的实数x,y的值为( )。

A.x=0且y=3 B.x=0且y=-3

C.x=5且y=2 D.x=3且y=0

4.复数(2x2+5x+2)+(x2+x-2)i为虚数,则实数x满足( )。

5.已知复数z1=2-ai(a∈R)对应的点在直线x-3y+4=0上,则复数z2=a+2i对应的点在( )。

A.第一象限 B.第二象限

C.第三象限 D.第四象限

6.(广西钦州市2018届高三上学期第一次质量检测)已知复数z=1+i,则下列命题中正确的个数为( )。

A.1 B.2 C.3 D.4

7.已知0＜a＜2,复数z=a+i(i是虚数单位),则|z|的取值范围是( )。

A.(1,3) B.(1,5)

C.(1,3) D.(1,5)

A.1-2i B.2-i

C.2+i D.1+2i

A.1-2i B.-1+2i

C.3+4i D.-3-4i

10.若复数z1=1+5i,z2=-3+7i,则复数z=z1-z2在复平面内对应的点在( )。

A.第一象限 B.第二象限

C.第三象限 D.第四象限

A.32i B.-32i C.-32 D.32

经过几年的发展，宿州市现代农业产业化联合体已从最初的16家增加到272家，覆盖了粮食、畜禽、果蔬、林木等主导产业，年产值达290亿元以上。随着各类联合体不断涌现，农业经营主体通过生产要素相互融合，进一步实行优势互补、风险共担，形成了“你中有我，我中有你”的一体化格局，实现了“1+1+1＞3”的融合效应。例如，埇桥区淮河粮食产业联合体中的担保与反担保方式形成了资金融合。

A.第一象限 B.第二象限

C.第三象限 D.第四象限

A.i B.-i C.1 D.-1

14.已知|z|=3,且z+3i是纯虚数,则z等于( )。

A.-3i B.3i C.±3i D.4i

15.满足条件|z-i|=|3+4i|的复数z在复平面内对应点的轨迹是( )。

A.一条直线 B.两条直线

16.在平行四边形ABCD中,对角线AC与BD相交于点O,若向量对应的复数分别是3+i,-1+3i,则对应的复数是( )。

A.2+4i B.-2+4i

C.-4+2i D.4-2i

17.|(3+2i)-(1+i)|表示( )。

A.点(3,2)与点(1,1)之间的距离

B.点(3,2)与点(-1,-1)之间的距离

C.点(3,2)到原点的距离

D.以上都不对

18.已知复数z1=m+2i,z2=3-4i,若为实数,则实数m的值为( )。

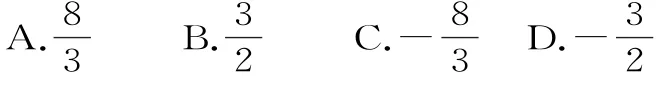
19.已知关于x的方程x2+(1-2i)x+3m-i=0有实根,则实数m满足( )。

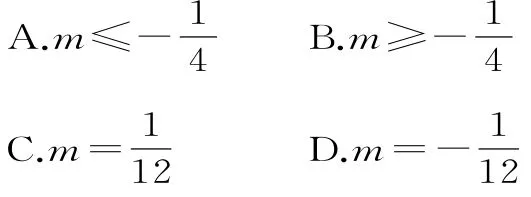
A.第一象限 B.第二象限

C.第三象限 D.第四象限

21.设(1+i)x=1+yi,其 中x,y 是 实数,则|x+yi|=( )。

22.(广东中山市第一中学2018届高三第二次统考)若复数z=(a+i)2(a∈R)在复平面内对应的点在y轴上,则|z|=( )。

A.1 B.3 C.2 D.4

A.1 B.-1 Ci. D.-i

24.(广西桂林市第十八中学2018届高三上学期第三次月考)已知复数z满足(1+i)z=(1-i)2,则|z|=( )。

A.-2i B.-2

C.2 D.-1-i

25.(辽宁凌源二中2018届高三三校联考)记复数z的虚部为Im(z),已知复数z=-2i(i为虚数单位),则Im(z)为( )。

A.-3 B.2 C.-3i D.3

Ci. D.1

27.(河南省中原名校2018届高三上学期第一次质量考评)设复数z=-2+i(i是虚数单位),z的共轭复数为,则|(1+z)·|等于( )。

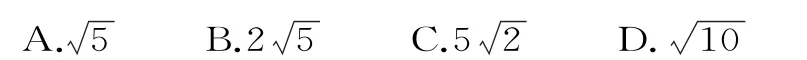
28.若(a-2i)i=b-i,其中a,b∈R,i是虚数单位,则复数z=a+bi的模等于( )。

29.若z1,z2∈C,则是( )。

A.纯虚数 B.实数

C.虚数 D.实数或虚数

30.(广东珠海一中等六校2018届高三第一次联考)欧拉公式eix=cosx+isinx(i为虚数单位)是由瑞士著名数学家欧拉发明的,它将指数函数的定义域扩大到复数,建立了三角函数和指数函数的关系,它在复变函数论里占有非常重要的地位,被誉为“数学中的天桥”。根据欧拉公式可知,e2i表示的复数在复平面中位于( )。

A.第一象限 B.第二象限

C.第三象限 D.第四象限

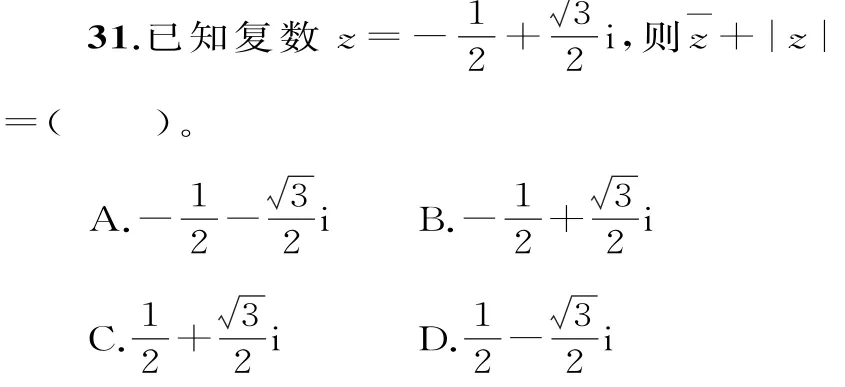
32.(广东德庆县香山中学2018届高三理科数学第一次模拟)已知0＜a＜3,复数z的实部为a,虚部为1,则|z|的取值范围是( )。

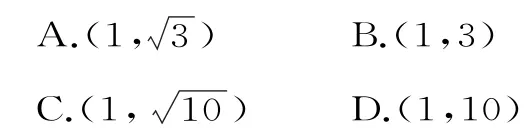
33.(重庆铜梁县第一中学2018届高三九月月考)设复数其中i是虚数单位,若为纯虚数,则实数a=( )。

34.若A,B为锐角三角形的两个内角,则复数z=(cosB-sinA)+(sinB-cosA)i对应的点位于复平面内的( )。

A.第一象限 B.第二象限

C.第三象限 D.第四象限

35.设复数z1,z2在复平面内的两对应点关于虚轴对称,若z1=1-2i,其中i是虚数单位,则的虚部为( )。

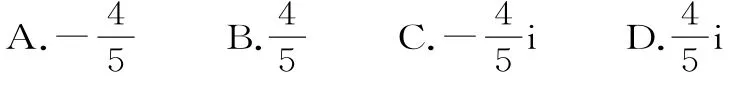
36.(河南林州市第一中学2018届高三八月调研)已知复数数单位),则在复平面内,复数z所对应的点位于( )。

A.第一象限 B.第二象限

C.第三象限 D.第四象限

A.第一象限 B.第二象限

C.第三象限 D.第四象限

38.复数z满足条件:|2z+1|=|z-i|,那么z对应的点的轨迹是( )。

A.圆 B.椭圆

C.双曲线 D.抛物线

39.已知复数z=(x-2)+yi(x,y∈R)在复平面内对应的向量的模为3,则y的最x大值是( )。

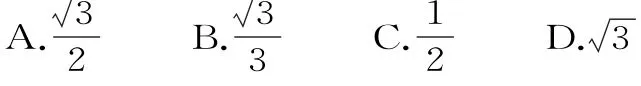
40.设z=(2t2+5t-3)+(t2+2t+2)i,t∈R,则以下结论正确的是( )。

Az.对应的点在第一象限

Bz.一定不为纯虚数

Dz.一定为实数

二、填空题

41.以-2+3i的虚部为实部,以3i2+的实部为虚部的复数是____。

42.若a-2i=bi+1(a,b∈R),则b+ai=___。

43.已知z1=-4a+1+(2a2+3a)i,z2=2a+(a2+a)i,其中a∈R。若z1＞z2,则a的取值集合为____。

45.已知x∈R,y∈R,(xi+x)+(yi+4)=(y-i)-(1-3xi),则x=____,y=____。

46.(浙江嘉兴市第一中学2018届高三九月基础测试)若复数z=4+3i,其中i是虚数单位,则|z|=____,z2=____。

47.已知复数z1=-m+m2i,若z1+z2＞0,则实数m=____。

49i.是虚数单位,i+i2+i3+i4+…+i2018=____。

52.(江西临川第二中学2018届高三上学期期中测试)已知b为实数,i为虚数单位,若为实数,则b=____。

54.设实数x,y,θ满足以下关系:x+yi=3+5cosθ+i(-4+5sinθ),则x2+y2的最大值是____。

56.设复数z1、z2在复平面内的对应点分别为A、B,点A与B关于x轴对称,若z1(1-i)=3-i,则|z2|=____。

57.设复数z1、z2满足z1-=-1+i,z1=(a+2)+(a2+a-2)i为不等于0的实数,则|z2|=____。

58.投掷两颗骰子,其向上的点数分别为m和n,则复数(m+ni)2为纯虚数的概率为____。

三、解答题

61.设m∈R,复数z=2m2-3m-2+(m2-3m+2)i。试求当m为何值时,z分别为:

(1)实数;

(2)虚数;

(3)纯虚数。

(1)z∈R;

(2)z是纯虚数;

(3)z对应的点位于复平面第二象限;

(4)z对应的点在直线x+y+3=0上。

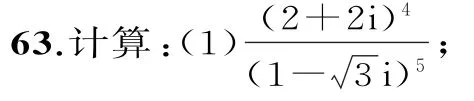
(2)(2-i)(-1+5i)(3-4i)+2i。

65.(1)已知复数z在复平面内对应的点在第四象限,|z|=1,且z+=1,求z;

(1)求|z1|及|z2|,并比较大小;

(2)设z∈C,判断满足条件|z2|≤|z|≤|z1|的对应点Z的轨迹是什么图形。

70.将一颗质地均匀的正方体骰子(六个面的点数分别为1、2、3、4、5、6)先后抛掷两次,记第一次出现的点数为a,第二次出现的点数为b。

(1)设复数z=a+bi(i为虚数单位),求事件“z-3i为实数”的概率;