复数单元检测题（B卷）答案与提示

一、选择题

1.B 2.B 3.A 4.D 5.B 6.C 7.B 8.D 9.D 10.D 11.D 12.A 13.C 14.B 15.C 16.D 17.A 18.D 19.C 20.B 21.B 22.C 23.A 24.C 25.A 26.D 27.D 28.D 29.B 30.B 31.D 32.C 33.C 34.B 35.A 36.D 37.A 38.A 39.D 40.C

二、填空题

59.1,-3 60.-1

三、解答题

61.(1)当z为实数时,则有m2-3m+2=0,解得m=1或2。

故m为1或2时,z为实数。

(2)当z为虚数时,则有m2-3m+2≠0,解得m≠1且m≠2。

故m≠1且m≠2时,z为虚数。

62.由定义可知,假设复数z=a+bi(a,b∈R),当且仅当b=0时,z∈R;当且仅当a=0且b≠0时,z为纯虚数;当a＜0,b＞0时,z对应的点位于复平面的第二象限;复数z对应的点的坐标是直线方程的解,则这个点就在这条直线上。

(1)由m2+2m-3=0且m-1≠0,得m=-3。故当m=-3时,z∈R。

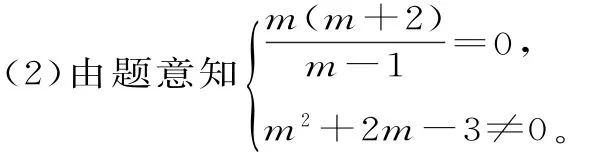
解得m=0,或m=-2。

故当m=0或m=-2时,z为纯虚数。

故当m=0或m=-2时,z对应的点在直线x+y+3=0上。

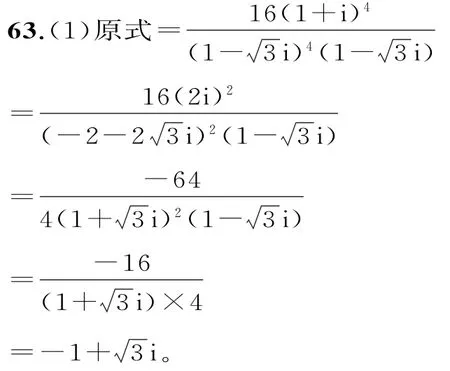
故当m＜-3时,z对应的点位于复平面的第二象限。

(2)原式=(3+11i)(3-4i)+2i=53+21i+2i=53+23i。

64.因为z=1+i,所以z2=2i。

65.(1)设z=a+bi(a、b∈R)。

因为2m2-5m-3≠0,所以m≠3。

因此,m=-2。

所以|z1|＞|z2|。

(2)由|z2|≤|z|≤|z1|及(1)知1≤|z|≤2。

因为|z|的几何意义就是复数z对应的点到原点的距离,所以|z|≥1表示|z|=1所表示的圆外部所有点组成的集合,|z|≤2表示|z|=2所表示的圆内部所有点组成的集合,故符合题设条件点的集合是以O为圆心,以1和2为半径的两圆之间的圆环(包含圆周),如图1所示。

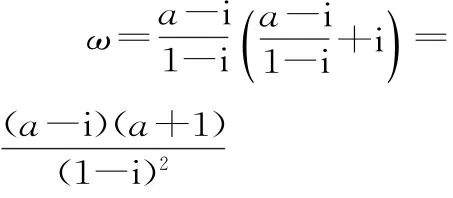
图1

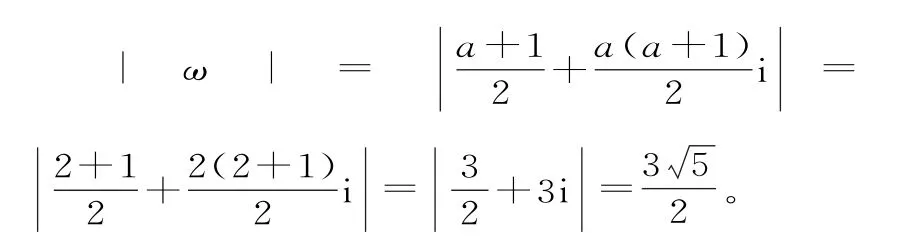
69.(1)ω=(1+i)2+3(1-i)-4=-1-i,所以|ω|=2。

(2)由条件,得

所以(a+b)+(a+2)i=1+i。

70.(1)z=a+bi(i为虚数单位),z-3i为实数,则a+bi-3i=a+(b-3)i为实数,则b=3。

依题意得b的可能取值为1、2、3、4、5、6,故b=3的概率为。

(2)连续抛掷两次骰子所得结果如表1:

表1

由上表知,连续抛掷两次骰子共有36种不同的结果。

不等式组所表示的平面区域如图2中阴影部分所示(含边界)。

由图知,点P(a,b)落在四边形ABCD内的结果有:(1,1)、(1,2)、(1,3)、(2,1)、(2,2)、(2,3)、(2,4)、(3,1)、(3,2)、(3,3)、(3,4)、(3,5)、(4,1)、(4,2)、(4,3)、(4,4)、(4,5)、(4,6),共18种。

所以点P(a,b)落在四边形ABCD内(含边界)的概率为

图2