数学归纳法应用探究
■河南省实验中学 殷珂宇
学习数学离不开基本的思想方法,解数学高考题更要讲究思想方法,否则寸步难行。数学归纳法是高中数学的基本方法之一,“考纲”不仅要求我们掌握数学归纳法的原理及其步骤,还要求我们能用数学归纳法证明一些简单的数学命题。那么,什么是数学归纳法呢?
一般地,证明一个与正整数n有关的命题,可按下列步骤进行:
(1)(归纳奠基)证明当n取第一个值n0(n0∈N+)时命题成立;
(2)(归纳递推)假设n=k(k≥n0,k∈N+)时命题成立,证明当n=k+1时命题也成立。
只要完成这两个步骤,就可以断定命题对从n0开始的所有正整数n都成立。上述证明方法叫作数学归纳法。
那么,数学归纳法能帮助我们破解哪些问题呢?
一、利用数学归纳法证明等式
例1 已知n∈N+,证明:1
思路分析:等式的左边有2n项,右边有n项,左边的分母是从1到2n的连续正整数,末项与n有关,右边的分母是从n+1到n+n的连续正整数,首、末项都与n有关。
②假设当n=k(k∈N+)时等式成立,即:
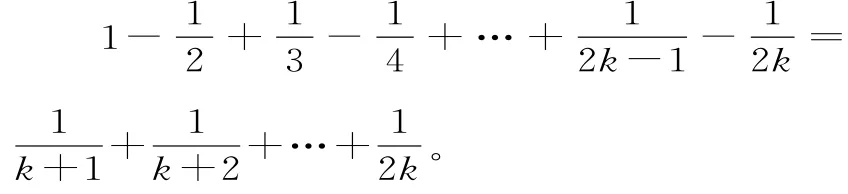
那么当n=k+1时:
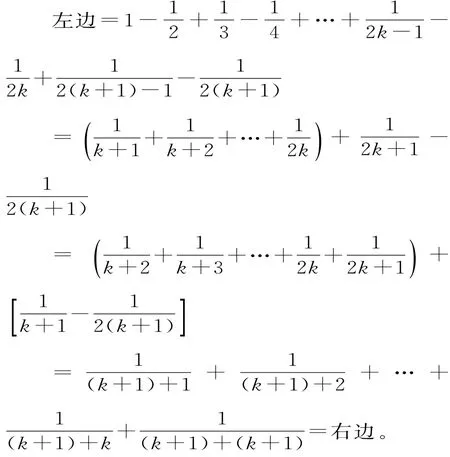
所以当n=k+1时等式也成立。
综合①②知对一切n∈N+,等式都成立。
感悟与总结:用数学归纳法证明恒等式应注意:明确初始值n0的取值并验证n=n0时命题的真假(必不可少)。“假设n=k(k∈N+且k≥n0)时命题正确”,写出命题形式,分析“n=k+1时”命题是什么,并找出与“n=k”时命题形式的差别。弄清左端应增加的项,明确等式左端变形目标,掌握恒等式变形常用的方法:乘法公式、因式分解、添拆项、配方等。
二、用数学归纳法证明不等式

思路分析:由“an+1=f(an),数列 {bn} 满足”找到bn与bn+1之间的关系。

感悟与总结:应用数学归纳法证明不等式应注意两个问题:(1)当遇到与正整数n有关的不等式证明时,若应用其他方法不容易证,则可考虑应用数学归纳法;(2)用数学归纳法证明不等式的关键是由n=k时成立,推证n=k+1时也成立,证明时用上归纳假设后,可采用分析法、综合法、求差(求商)比较法、放缩法等证明。
三、用数学归纳法证明整除问题
例3 用数学归纳法证明42n+1+3n+2能被13整除,其中n为正整数。
思路分析:当n=k+1时,把42(k+1)+1+3k+3配凑成42k+1+3k+2的形式是解题的关键。
证明:(1)当n=1时,42×1+1+31+2=91能被13整除。
(2)假设当n=k(k∈N+)时,42k+1+3k+2能被13整除,则当n=k+1时:

所以当n=k+1时命题也成立。
由(1)(2)知,当n∈N*时,42n+1+3n+2能被13整除。
感悟与总结:用数学归纳法证明整除问题时,P(k)⇒P(k+1)的整式变形是个难点,可找出它们之间的差异,然后将P(k+1)进行分拆、配凑成P(k)的形式,也可运用结论:“P(k)能被p整除且P(k+1)-P(k)能被p整除⇒P(k+1)能被p整除”。应用数学归纳法证明整除性问题主要分为两类:一是整除数,二是整除代数式。这两类证明最关键的问题是“配凑”要证的式子(或是叫作“提公因式”),即当n=k+1时,将n=k时假设的式子提出来,再变形,然后进行证明。
四、用数学归纳法破解“归纳—猜想—证明”问题
例4 已知数列{an}中,a1=5,Sn-1=an(n≥2且n∈N*)。
(1)求a2,a3,a4,并由此猜想an的表达式。
(2)用数学归纳法证明{an}的通项公式。
思路分析:可以先从观察入手,发现问题的特点,以形成解决问题的初步思路,然后用归纳的方法进行试探,提出猜想,最后用数学归纳法给出证明。
解:(1)a2=S1=a1=5,a3=S2=a1+a2=10,a4=S3=a1+a2+a3=20。
猜想:an=5×2n-2(n≥2,n∈N*)。
(2)证明:①当n=2时,a2=5×22-2=5成立。
②假设当n=k时猜想成立,即ak=5×2k-2(k≥2且k∈N*),则n=k+1时,ak+1=Sk=a1+a2+…+ak=5+5+10+…+5×
故当n=k+1时,猜想也成立。
由①②可知,对n≥2且n∈N*,都有an=5×2n-2。
感悟与总结:解决数学归纳法中“归纳—猜想—证明”问题及不等式证明时,以下几点容易造成失分,我们应高度重视:
(1)归纳整理不到位得不出正确结果,从而给猜想造成困难。
(2)证明n=k到n=k+1这一步时,忽略了假设条件去证明,造成使用的不是纯正的数学归纳法。
(3)不等式证明过程中,不能正确合理地运用分析法、综合法来求证。
实际上,只要我们理解和掌握了基础知识,多思考,多探究,熟练掌握数学归纳法中几种常见的推证技巧,就能快速正确地解决问题。

