为数学点赞——名师例析数学文化（3）复数篇

■北京市第十二中学高中部 高慧明

■北京教育学院丰台分院 张 琦

图1

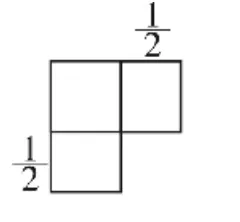
图2

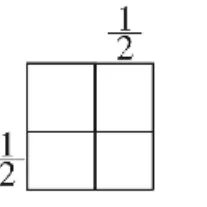
图3

《普通高中数学课程标准》(征求意见稿2016)中将课程内容分为必修课程、选修Ⅰ和选修Ⅱ三部分内容。其中每部分内容又包括函数、几何与代数、统计与概率、数学建模活动与数学探究活动四部分内容(注:必修课程还包括预备知识)。其中复数与平面向量及应用、立体几何初步共同构成了必修课程的几何与代数部分。

课程标准对复数部分的教学要求是:“在复数的教学中,应注重对复数的表示及几何意义的理解,避免烦琐的计算与技巧训练。对于感兴趣的学生,可以安排一些引申的内容,如复数的三角形式等。可以适当地融入数学文化,让学生体会数系扩充过程中理性思维的作用。”下面拟通过回顾复数的发展历史,了解复数概念的重要发展阶段,体会数系扩充过程中的理性思维、反思意识和创新精神。

一、复数产生的大致历程

一元二次方程的历史可以追溯到古巴比伦时期,在大英博物馆所藏古巴比伦时期泥版BM13901上载有七个一元二次方程问题。其中第1题为:“正方形面积与一边长之和为,求该正方形边长。”

古巴比伦人解决上述问题的方法是几何法,图1所示的是一边长为x的正方形,其边上接着一个长为1、宽也为x的长方形。之后将长方形按虚线剪开,剪下的一半置于正方形的另一边(如图2),然后补一个边长为的小正方形,即得一大正方形(图3),其面积为,故而大正方形边长为1,所以要求正方形的边长

从这个问题分析,可以发现古巴比伦人对一元二次方程有着深刻的理解,而且这种求一元二次方程根的方法对后世数学家研究一元二次方程问题有着深远的影响。而且如果深入分析这个问题,能够发现这种求解方法中并没有负根,这也与负数的发展历史有关,因为直到16、17世纪欧洲大多数数学家还不承认负数是数。

公元3世纪,被誉为古希腊代数学鼻祖的丢番图在其《算术》中提到这样一个问题:“已知两数的和与积,求这两个数。”丢番图的解法是:“假设两数的和为20,乘积为96,2x为所求数之差,于是所求数为10+x和10-x。故得10-x2=96,所以x=2,从而得所求两数分别为12和8。”这时候,人们已经知道一元二次方程有两个根,如果其中有一个根为负数时,自动舍掉。但如果其中有一个根为虚数时,宁可认为这个方程是不可解的。

公元9世纪,阿拉伯数学家花拉子米也用几何方法来解一元二次方程。在《代数学》中,花拉子米给出了求解一元二次方程x2+10x=39的两种几何方法。

更为重要的是,在该部著作中,花拉子米首次得出了一元二次方程ax2+bx+c=0(a≠0)的求根公式为欧洲国家应用一元二次方程的求根公式,首次见于法国数学家韦达所著的《分析五篇》一书,还只限于正根。虚根问题虽然是由求一元二次方程的解所引发的,但迫使人们认真对待复数却是因为求一元三次方程的解。意大利数学家卡尔达诺在1545年出版的著作《大术》中讨论了求解一元三次方程的代数方法,卡尔达诺区分了13种情况对一元三次方程进行了详细讨论,给出了13种求解的公式,现在称这些公式为卡尔达诺公式。

据说数学史上最早发现一元三次方程通式解的人,是16世纪意大利的另一位数学家尼柯洛·冯塔纳。经过多年的探索和研究,冯塔纳利用十分巧妙的方法,找到了一元三次方程一般形式的求根方法,从此名扬欧洲。但是冯塔纳不愿意将他的这个重要发现公之于世。

当时的卡尔达诺,对冯塔纳的发现非常感兴趣。他几次诚恳地登门请教,希望获得冯塔纳的求根公式。可是冯塔纳始终守口如瓶,滴水不漏。虽然卡尔达诺屡次受挫,但他极为执着,软磨硬泡地向冯塔纳“挖秘诀”。后来,冯塔纳终于用一种隐晦得如同咒语般的语言,把一元三次方程的解法“透露”给了卡尔达诺。冯塔纳认为卡尔达诺很难破解他的“咒语”,可是卡尔达诺的悟性太棒了,他通过解三次方程的对比实践,很快就彻底破译了冯塔纳的秘密。

卡尔达诺把冯塔纳的三次方程求根公式,写进了自己的学术著作《大术》中,但并未提到冯塔纳的名字。随着《大术》在欧洲的出版发行,人们才了解到三次方程的一般求解方法。由于第一个发表三次方程求根公式的人确实是卡尔达诺,因此后人就把这种求解方法称为卡尔达诺公式。我们下面简单介绍一下卡尔达诺公式。

设一般的一元三次方程为ay3+by2+cy+d=0(a≠0),方程两边同时除以a,原方程变为不妨记为y3+a1y2+a2y+a3=0,此时令y=x,为了方便,不妨记所以只需求方程x3+px+q=0的解即可。

此时,设x=u+v,则方程又变换为u3+v3+(3uv+p)(u+v)+q=0,为了操作简单,我们不妨再加一个限定条件。令3uv+p=0,即v=,再整理方程,变为u3+利用一元二次方程的求根公式,可得u3的两个根,再开立方,可得u的值,进而可得方程x3+px+q=0的根。

多么巧妙的解题过程啊!但是,如果深思一下在利用一元二次方程的求根公式的时候有两不等实根,但是当时呢?怎么办?

用现在的代数语言描述x3+px+q=0的三个根为:

在应用公式求解的时候出现了十分尴尬的情况:即使一元三次方程的三个根都是实数,但用公式求解的时候会出现虚数。比如,x3-15x-4=0,容易验证4是方程的一个根,接下来还可以找到另外两个根-2±3,因此方程的三个根都是实数。但是,直接用卡尔达诺求解一元三次方程的公式计算方程根的过程中会得到一个根这个根是实数吗?这样的方程是有解还是无解呢?

为了解释清楚上面产生的困难,卡尔达诺写道:“显然,将10分成两部分,使它们的乘积等于40是不可能的。不过我们可以用这样的方式来求解。将10等分,得5,自乘得25。减去乘积自身(即40),得-15。从5中加上或减去该数的平方根即得乘积为40的两部分,所得的两个数分别为……抛开精神上的痛苦,将5+即40……这的确很矫揉造作,因为利用它我们并不能做在纯负数情形中所能做的运算。”(这均为今天的符号)

尽管卡尔达诺本人并不理解这种数,甚至拒绝了这种数,还说:“算术就是这样的精巧奇妙,它最根本的特点,正如我说过的,是既精妙又无用。”但毕竟这是具有历史意义的一刻,卡尔达诺成了数学史上第一个写下负数平方根的人。不经意的一笔却为虚数的发展播下了种子。

虚数(imaginarynumber)这个名称是法国哲学家、数学家笛卡儿给出的,笛卡儿认为方程的这些“虚”根是不能对应到任何数的。负根至少可以通过方程变换转化成“实”的,但是“虚”根却办不到。所以这些根不是实的,而是虚的,它们并不是数。并且,笛卡儿还给这些数取了一个不幸的名字——“虚数”,意思是“想象中的数”。

欧拉第一个使用符号i表示虚数,写在他1777年提交给圣彼得堡科学院的论文中,这篇论文直到1794年才发表。尽管欧拉已多次接触虚数,并且使用起来驾轻就熟,但对于虚数概念本身,他还是不甚了了,甚至还认为在他的《代数学引论》中,他写道:“因为所有可以想象的数要么大于零,要么小于零,要么等于零,所以负数的平方根显然是不能包含在这些数之中的。因此我们必须说,它们是不可能的数。……它们通常被称为想象的数,因为它们只存在于想象之中。”

在复数理论发展的过程中,德国数学家高斯做出了巨大的贡献,他在1831年,建立了复数的某些运算,使得复数的运算也像实数一样“代数化”。他又在1832年第一次提出了“复数”(complexnumber)这个名词,高斯认为必须将虚数别开来,才引入了复数这个词。还将表示平面上同一点的两种不同方法——直角坐标法和极坐标法加以综合,统一于表示同一复数的代数式和三角式两种形式中,并把数轴上的点与实数一一对应,扩展为平面上的点与复数一一对应。高斯不仅把复数看作平面上的点,而且还看作是一种向量,并利用复数与向量之间一一对应的关系,阐述了复数的几何加法与乘法。至此,复数理论才比较完整和系统地建立起来了。

只有给出复数的几何表示,人们才真正感觉到了复数的存在,才心安理得地接受了复数。1797年,丹麦测量学家韦塞尔在丹麦皇家科学院宣读了一篇关于复数的论文,文中引入了虚轴并把复数表示为平面向量。但直到100年后的1897年,韦塞尔的丹麦文的论文被翻译为法文后,复数几何表示的工作才引起数学界的广泛重视。

1806年,瑞士数学家阿甘德首先把这类新数表示成三角形式并把它们与平面内线段的旋转结合起来,例如分别被看成单位线段按照逆时针与顺时针方向旋转90度所得的结果。可以这样理解:一个实数乘以1,相当于原地没动;乘以-1,相当于向后转;乘以i,相当于向左转;乘以-i,相当于向右转,这是复数的乘法。再来考虑复数的加法,+5,向右走5个单位;-5,向左走5个单位;+5i向上走5个单位;-5i向下走5个单位。复数的表达方式已经被广泛应用于流体力学、信号分析等,有着深厚的物理背景。在复数的基础上,英国数学家哈密顿构造了四元数,并导致了物理学中著名的麦克斯韦方程的产生。

虚数概念的引入在数学史上是一个曲折的过程,其中充满着数学家的想象力、创造力和不屈不挠、精益求精的精神。

二、数系的扩充和复数的概念

自从有了人类,为了统计捕获的猎物和采集的野果等方面的需要,用手指、十字或刻痕来数个数,经历了漫长的岁月,创造了自然数,1,2,3,4,5…。后来人们把表示“无”的0也归入自然数,形成了自然数集,自然数集是产生其他一切数的源泉,所有其他数都是由其扩充得到的。

但是随着时代的发展,在分配某些物品的时候,人们发现只有自然数是不够用的,比如,四个人平分一个西瓜,把西瓜切成相同的四份,每人得到其中的一份,怎么用数表示这一份呢?诸如此类的问题很多。

于是,自然引出了分数,从解方程的角度,分数是这样引入的:如果3x=5,这个方程在自然数的范围内无解,为了解决这个矛盾,数的范围必须扩充。所以定义:如果m,n(n≠0)是自然数,如果数量a满足条件a×n=m,则称a是分数,记作

时代又在发展,智慧的人类发现仅有分数也是不够的。比如用自然数表示了收入,那么支出应该怎么表示呢?用分数表示了上升的程度,那么下降程度又该如何描述呢?于是,引入了相反数的概念——与正数相反的概念。设a是分数(两个自然数之比),方程x+a=0在分数范围内无解,为了解决这个矛盾,数的范围又得扩充。所以,我们定义方程x+a=0的解叫作a的相反数,记作-a,于是数的范围扩大到包括分数和它的相反数的新数集——有理数集。

古希腊时期的毕达哥拉斯学派有个基本的观点——“万物皆数”,他们相信任何的量都能表示成两个整数之比。但是学派中的一个青年希帕苏斯却发现正方形的边长与对角线之比不能用整数比表示,即 2不是分数。他百思不得其解,最后认定这是一个从未见过的新数。这个新数的发现,使毕达哥拉斯学派感到震惊,动摇了他们哲学思想的核心。无理数的发现,击碎了毕达哥拉斯学派“万物皆数”的理想。同时暴露出有理数系的缺陷:一条直线上的有理数尽管“稠密”,但是它却漏出了许多“孔隙”,而且这种“孔隙”多得“不可胜数”。这样,古希腊人把有理数视为是连续衔接的那种设想,就彻底地破灭了。

无理数是什么?人民教育出版社教材中的无理数的定义如下:

八年级上册:任何一个有理数可以写成有限小数和无限不循环小数的形式,3即3.0,即-0.6…很多平方根和立方根都是无限不循环小数,无限不循环小数又叫无理数。有理数和无理数统称为实数。

从有理数到无理数,也可以看成是两个方面需求的结果:一是度量线段过程中发现的存在着不可公度线段——每一条这样的线段都对应着借助于单位长度而给出的一个数,这样的数就是无理数。二是从数学内部的需求看,与有理数域的扩充类似,为了解像x2=2这样的方程,需要构造一个比有理数集更广的实数集。

从实数到复数,主要是数学内部的需求,也就是上面所述在一元三次方程求解过程中产生的 -1的问题,于是从数学的角度,只好引进一种新的数——“虚数单位”i,它服从i2=-1,之后要定义它的运算;定义了运算,又要研究它的运算律。从而数集就从实数集又扩充到了复数集。

上述数的范围的扩充过程,反映了数学推广过程的一个重要特性——使得在原来范围内成立的规律在更大的范围内仍然成立。非常幸运,从自然数到有理数,有理数集到实数集,实数集到复数集,完全满足这个要求。

复数除了在高考和竞赛中的简单应用外,随着科学和技术的进步,复数理论已越来越显出它的重要性,它不但对于数学本身的发展有着极其重要的意义,而且为证明机翼上升力的基本定理起到了重要作用,并在解决堤坝渗水的问题中显示了它的威力,也为建立巨大水电站提供了重要的理论依据。