合情推理与演绎推理热点题型解读

■海南省万宁市北京师范大学万宁附属中学 陈情君

推理是每年高考常考的考点也是高考的重点和热点之一。推理一般包括合情推理与演绎推理,其中合情推理又包括了归纳推理和类比推理。推理的考查形式常以填空题、选择题为主,考査内容较为基础,主要体现能力要求,常结合函数、方程、数列、不等式、解析几何与立体几何进行考查,考法灵活,综合性强,下面逐一解读。

一、归纳推理

(一)定义

由某类事物的部分对象具有某些特征,推出该类事物的全部对象都具有这些特征的推理,或者由个别事实概括出一般结论的推理,称为归纳推理。

(二)归纳推理的特点

(1)归纳推理是由部分到整体、由个别到一般的推理。

(2)归纳推理的前提是部分的、个别的事实,因此归纳推理的前提和结论之间的联系是或然的,所以“前提真而结论可能为假”。

(三)运用归纳推理的一般步骤

(1)通过观察特例发现某些相似性(特例的共性或一般规律)。

(2)把这种相似性推广为一个明确表述的一般性命题(猜想)。

(3)对所得出的一般性命题进行检验。在数学上,检验的标准是能否进行严格的证明。

题型一：与数字(数列)有关的等式的推理

例1 (2017年宁波模拟)观察下列等式,13+23=32,13+23+33=62,13+23+33+43=102,根据上述规律,13+23+33+43+53+63=( )。

A.192B.202C.212D.222

解析：因为13+23=32,13+23+33=62,13+23+33+43=102,等式的右端依次为(1+2)2,(1+2+3)2,(1+2+3+4)2,所以13+23+33+43+53+63=(1+2+3+4+5+6)2=212,故选C。

评注:从所给等式的结构入手,观察数字特点,发现等号两侧数据的形式及底数之间的关系是快速求解的关键。

题型二：与图形变化有关的推理

例2 某种平面分形图如图1所示,一级分形图是由一点出发的三条线段,长度相等,两两夹角为120°;二级分形图是在一级分形图的每条线段末端出发再生成两条长度为原来的线段,且这两条线段与原线段两两夹角为120°,…,依此规律得到n级分形图。

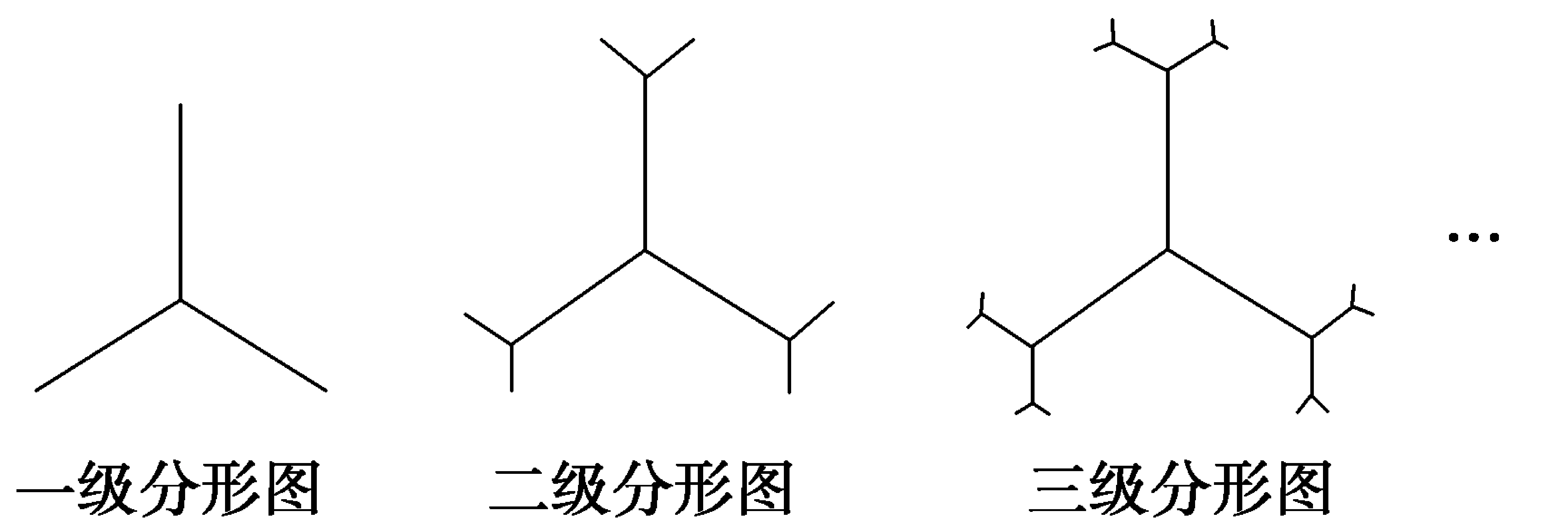
图1

n级分形图中共有____条线段。

解析：分形图的每条线段的末端出发再生成两条线段,由题图知,一级分形图有3=3×2-3条线段,二级分形图有9=3×22-3条线段,三级分形图中有21=3×23-3条线段,按此规律n级分形图中的线段条数an=3×2n-3(n∈N*)。

评注:与图形变化有关的推理主要包括图形数目归纳和图形变化规律归纳,应充分利用特殊图形变化规律归纳推理得出结论,并用赋值检验法验证其真伪性。

题型三：与不等式(式子)有关的推理

评注:细心观察每个不等式的特点,纵向看式与式之间变化规律,善于发现不等号右端分子、分母的变化与排序之间的关系,同时还要联系相关的知识找出其变化规律。

题型四：与周期性相关的推理

例4 两旅客坐火车外出旅游,希望座位连在一起,且有一个靠窗,已知火车上的座位如图2所示,则下列座位号码符合要求的应当是( )。

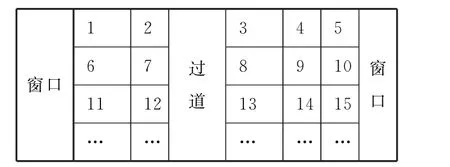
图2

A.48,49 B.62,63

C.75,76 D.84,85

解析：由已知图形中座位的排序规律可知,被5除余1的数和能被5整除的座位号靠窗,由于两旅客希望座位连在一起,且有一个靠窗,分析选项中的4组座位号知,A、B两组座位号都不靠窗,C中两个座位没有连在一起,只有D符合条件。

评注:若一组数据有“周而复始”的规律,则其具有周期性。本题背景是大家熟悉的火车座位问题,靠窗的座位号有明显的规律,最左边的座位号被5除余1,最右侧的座位号能被5整除。

题型五：与函数(方程)相关的推理

例5 给出下列命题:

……

请观察上面命题,猜想出命题n(n是正整数)为____。

解析：观察题中给出的命题易知,命题n中交点坐标为(n,n2),直线方程为y=nx,双曲线方程为故猜想命题n:点(n,n2)是直线y=nx与双曲线

评注:通过分析命题1、2、3中点的横纵坐标间的关系总结规律,并从中发现点的横坐标与直线y=kx的斜率k及双曲线y=m x

中m之间的联系,可以推出一个明确表述的一般性命题。

二、类比推理

(一)定义

类比推理是在两类不同的事物之间进行对比,找出若干相同或相似点之后,推测在其他方面也可以存在相同或相似之处的一种推理模式,类比推理也是合情推理的一种。

(二)类比推理的特点

(1)类比是以旧有认知作基础,从已经掌握的事物的属性推测正在研究中的事物新的属性。

(2)类比是从一种事物的特殊属性推测另一种事物的特殊属性。

(3)类比的结果是猜测性的,即可能真,也可能假,但它却具有发现的功能。

(三)运用类比推理的一般步骤

(1)找出两类事物之间的相似性或一致性。

(2)用一类事物的性质推测另一类事物的性质,得出一个明确的命题(猜想)。

(3)检验猜想。

题型六：平面与空间的类比

例6 现有一个关于平面图形的命题:如图3所示,同一个平面内有两个边长都是a的正方形,其中一个正方形的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为类比到空间,有两个棱长均为a的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒_____为 。

解析：在已知的平面图形中,中心O到两边的距离相等(如图4),即OM=ON。四边形OPAR是圆内接四边形,Rt△OPN≌Rt△ORM,因 此 S四边形OPAR同样地,类比到空间,如图5。两个棱长均为a的正方体重叠部分的体积为

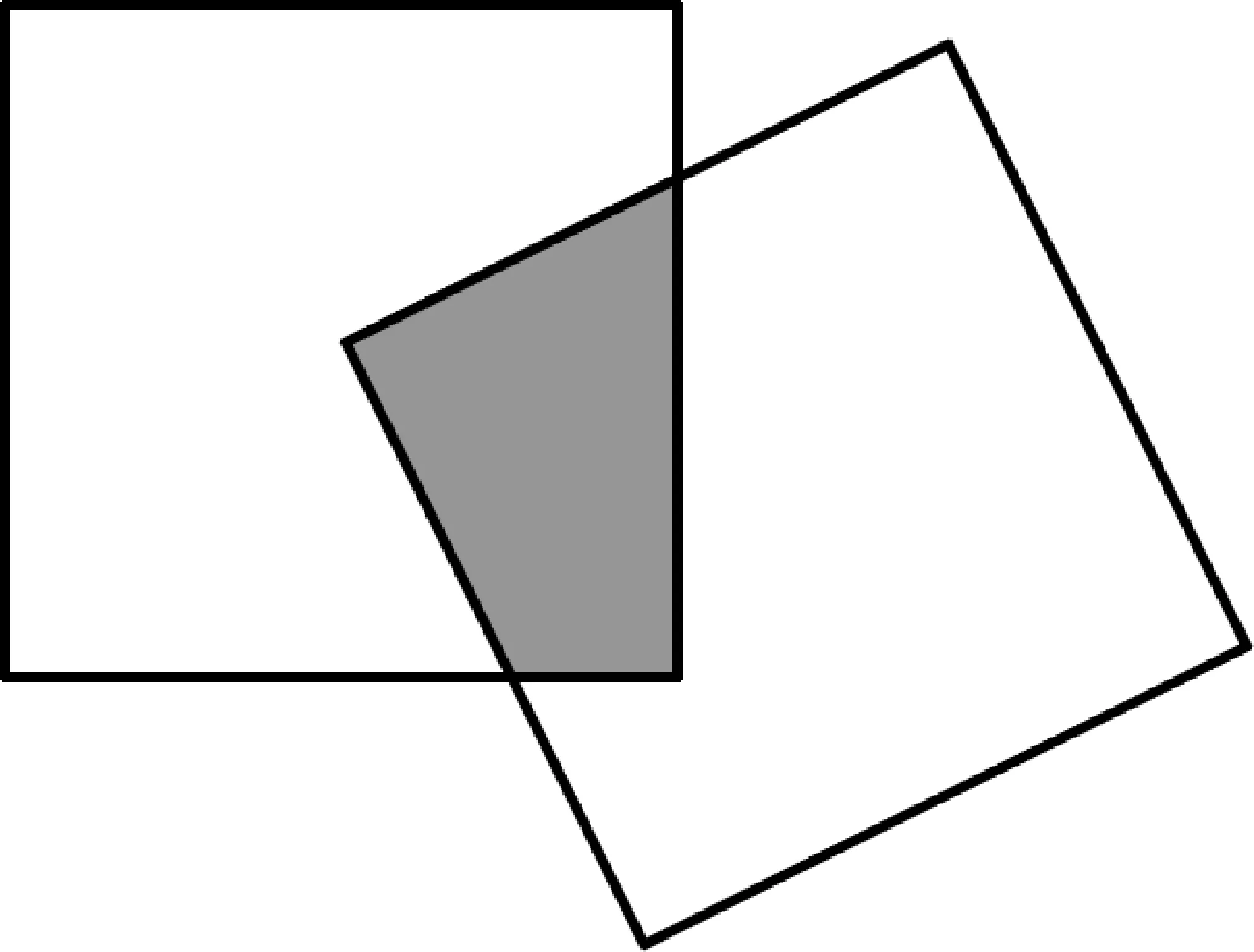
图3

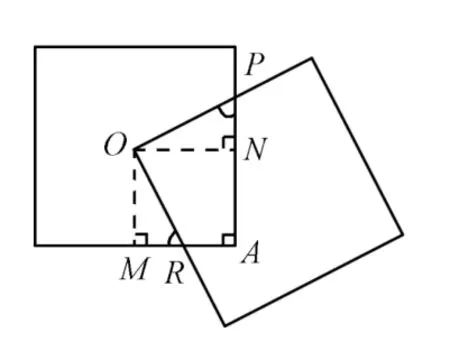
图4

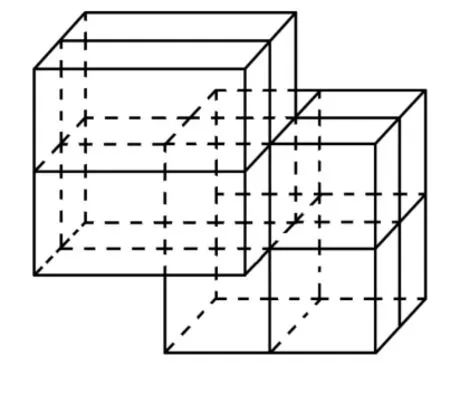
图5

评注:平面元素与空间中元素的类比找两类对象的对应元素是关键,如:点对应线,线对应面,面积对应体积,三角形对应三棱锥,圆对应球,平面角对应空间角,周长对应表面积等。

题型七：等差数列与等比数列性质的类比

例7 若数列{an}是等差数列,则数列是等差数列。类比这一性质可知,若正项数列{cn}是等比数列,且{dn}也是等比数列,则dn的表达式应为( )。

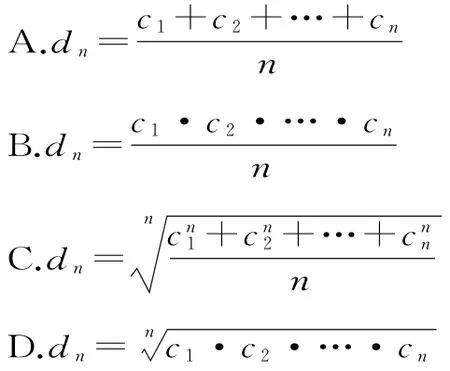
解析：若{an}是等差数列,则a1+a2+…即{b}为等差数列。若{c}是等nn,故 dn=nc1·c2·…·cn=为等比数列,故选D。

评注:从一个特殊式子、一个特殊图形的性质入手,提出类比推理型问题,求解时要认真分析两者间的联系与区别,深入思考两者的转化过程是求解的关键。等差与等比数列之间的类比,通常从商类比到开方,从和类比到积,从算术平均数类比到几何平均数,易知本题dn的表达式为

题型八：解题方法迁移的类比

例8 对于问题“已知关于x的不等式ax2+bx+c＞0的解集为(-1,2),解关于x的不等式ax2-bx+c＞0”,给出如下一种解法:

解:由ax2+bx+c＞0的解集为(-1,2),得a(-x)2+b(-x)+c＞0的解集为(-2,1),即关于x的不等式ax2-bx+c＞0的解集为(-2,1)。

解析：由ax2+bx+c＞0的解集为(-1,2),得a(-x)2+b(-x)+c＞0的解集为(-2,1),发现-x∈(-1,2),则x∈(-2,1)。若关于x的不等式则关于x的可看成由前一个不等式中的x用替换得到的,则(1,2)。

评注:方法类比应用到其他问题的求解中,应注意知识的迁移性。本题用来类比的是一元二次不等式的解法,用换元的思想将一元二次不等式中的x用换就可得出结论。

三、演绎推理

(一)定义

从一般性的原理出发,按照严格的逻辑法则,推出某个特殊情况下的结论的推理,叫作演绎推理。简言之,演绎推理是由一般到特殊的推理。

(二)演绎推理的特点

①演绎推理包含了三个命题,第一个命题称为大前提,它提供了一个一般性的原理;第二个命题称为小前提,它指出了一个特殊对象,两者结合起来,揭示了一般原理与特殊对象的内在联系,从而得到第三个命题——结论。

②演绎推理是一个必然性的推理,因而只要大前提、小前提及推理形式正确,那么结论一定是正确的,它是完全可靠的推理。

(三)一般模式

“三段论”是演绎推理的一般模式,常用的一种格式为:

①大前提——已知的一般原理;

②小前提——所研究的特殊情况;

③结论——根据一般原理,对特殊情况作出的结论。

题型九：根据多个语句信息推断结论

例9 (2017年湖北八校二联)有6名选手参加演讲比赛,观众甲猜测:4号或5号选手得第一名;观众乙猜测:3号选手不可能得第一名;观众丙猜测:1,2,6号选手中的一位获得第一名;观众丁猜测:4,5,6号选手都不可能获得第一名。比赛后发现没有并列名次,且甲、乙、丙、丁中只有1人猜对比赛结果,此人是( )

A.甲 B.乙 C.丙 D.丁

解析：根据题意,对于6名选手的比赛结果,甲、乙、丙、丁猜测如表1:

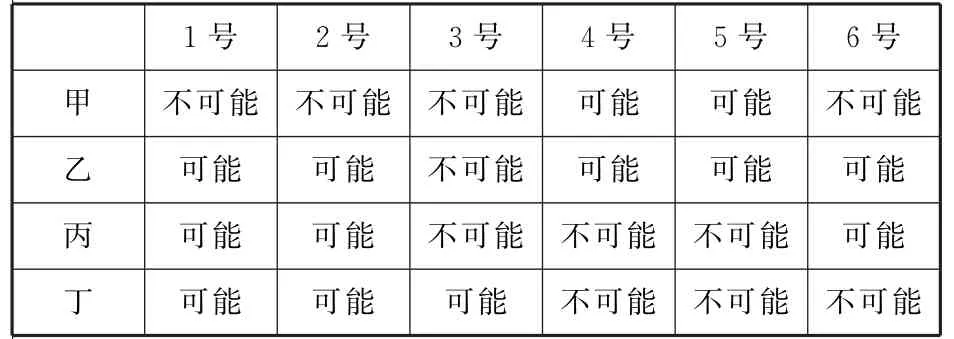
表1

由表知,只有丁猜对了比赛结果,故选D。

评注:求解多个语句的逻辑推理问题,需要善于从所给的诸多信息中抓住关键信息,以此为起点逐一分析推理,直到获得结论。列表法是解决此类题的常用方法,通过列表能清晰地看出彼此间的“矛盾”与“统一”。

题型十：三段论形式的推理

例10 (2017年福建三明调研)数列{an}的前n项和记为Sn,已知a1=1,an+1=

(2)Sn+1=4an。

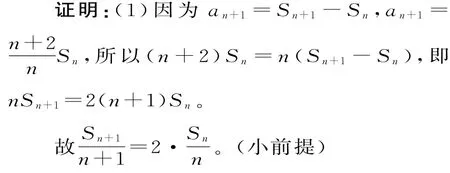
故是以2为公比,1为首项的等比数列。(结论)

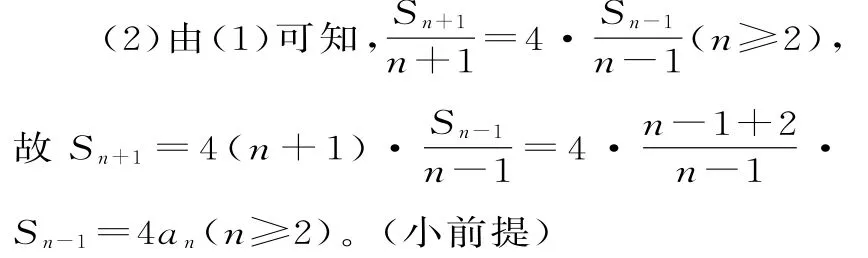
又a2=3S1=3,S2=a1+a2=1+3=4=4a1。(小前提)

所以,对于任意正整数n,都有Sn+1=4an。(结论)

评注:演绎推理的一般模式为三段论,三段论推理的依据是:如果集合M的所有元素都具有性质P,S是M的子集,那么S中所有元素都具有性质P。应用三段论解决问题时,首先应该明确什么是大前提、小前提,然后再找结论。

综上,从推理的形式和推理的正确性上讲,合情推理与演绎推理有差异;从二者在认识事物的过程中所发挥的作用的角度考虑,它们又是紧密联系,相辅相成的。合情推理的结论需要演绎推理的验证,而演绎推理的内容一般是通过合情推理获得的;演绎推理可以验证合情推理的正确性,合情推理可以为演绎推理提供方向和思路。

小试牛刀：

1.(2017年陕西模拟)观察下列式子:1,1+2+1,1+2+3+2+1,1+2+3+4+3+2+1,…,由以上可推测出一个一般性结论:对于n∈N*,1+2+…+n+…+2+1=____。

2.将自然数0,1,2,…按照如下形式进行摆列:

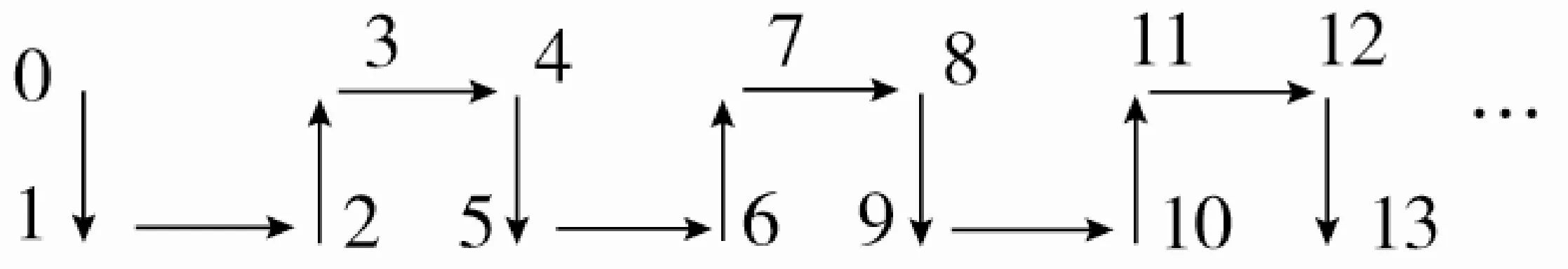
根据以上规律判定,从2016到2018的箭头方向是( )。

4.在平面几何中,△ABC的∠C的平分线CE分AB所成线段的比为这个结论类比到空间:在三棱锥A-BCD中(如图6),DEC平分二面角A-CD-B且与AB相交于E,则得到类比的结论是__。

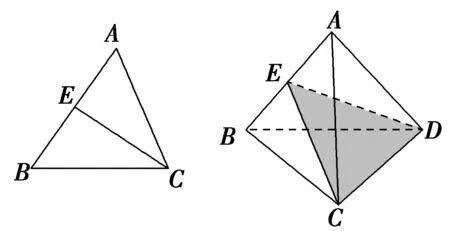
图6

5.某市为了缓解交通压力实行机动车辆限行政策,每辆机动车每周一到周五都要限行一天,周末(周六和周日)不限行。某公司有A,B,C,D,E五辆车,保证每天至少有四辆车可以上路行驶。已知E车周四限行,B车昨天限行,从今天算起,A,C两车连续四天都能上路行驶,E车明天可以上路,由此可知下列推测一定正确的是____。

①今天是周六 ②今天是周四 ③A车周三限行 ④C车周五限行

6.某西方国家流传这样一个政治笑话:“鹅吃白菜,参议员先生也吃白菜,所以参议员先生是鹅。”这个推理的结论显然是错误的,是因为( )。

A.大前提错误 B.小前提错误

C.推理形式错误 D.非以上错误

参考答案：1.n2

提示：1=12,1+2+1=22,1+2+3+2+1=32,1+2+3+4+3+2+1=42,…,故归纳可得1+2+…+n+…+2+1=n2。

2.A

提示：从所给的图形中观察得到规律:每隔四个单位,箭头的走向是一样的,比如说,0→1,箭头垂直指下,4→5,箭头也是垂直指下,8→9也是如此,而2016=4×504,所以2016→2017也是箭头垂直指下,之后2017→2018的箭头是水平向右,故选A。

3.nn

提示：第一个式子是n=1的情况,此时a=11=1;第二个式子是n=2的情况,此时a=22=4;第三个式子是n=3的情况,此时a=33=27;…归纳可知a=nn。

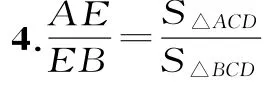
5.②

提示：因为每天至少有四辆车可以上路行驶,E车明天可以上路,E车周四限行,所以今天不是周三;因为B车昨天限行,所以今天不是周一,也不是周日;因为A,C两车连续四天都能上路行驶,所以今天不是周五、周二和周六,所以今天是周四。

6.C

提示：因为大前提的形式:“鹅吃白菜”不是全称命题,大前提本身正确;小前提“参议员先生也吃白菜”本身也正确,但是不是大前提下的特殊情况,鹅与人不能类比。所以不符合三段论推理形式,故这里的错误是推理形式错误。