例谈数列的差、比单调性的应用

■浙江省天台中学高二(2)班 褚凯佟 (指导老师:陈中停)

同学们有没有这样的体验:一些数列,它的相邻两项差或比构成的数列是具有单调性的。我们在尝试解决这种试题的时候,要是忘记或忽略了这个性质,就会导致解题走弯路甚至进入死胡同。

例题 已知数列{an}满足a1=用符号[x]表示不超过数x的最大整数。试求

我的思考历程如下：

裂项相消法求和：由2an+1=an2+2an推这是一个实质性的发现,没有它解决问题无从谈起,发现它使得目标和式可以求和了。

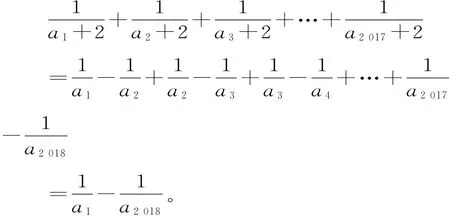
猜想结果：由于数列{an}是恒正、递增的数列,又二次函数f(x)=x2+2x在区间(0,+∞)是增函数,因此,估计a2018＞1,即,可以的结果是3。

下面证明a2018＞1。

如何用严谨的方法来证明a2018＞1呢?为解决这个问题,对式子2(an+1-an)=an2进行细心观察。由2(an+1-an)=结合a1(即a1≠0),得数列{an}是递增数列。又由{an}是递增数列,且an＞0,即an2是递增的,结合2(an+1-an)=an2,得数列{an+1-an}也是递增数列,即an+2-an+1＞an+1-an对于所有n恒成立。

这样,当n＞3时,有an-an-1＞an-1-an-2,an-1-an-2＞an-2-an-3,…,a3-a2＞a2-a1,a2-a1=a2-a1,上面所有式子同向相加得an-a1＞(n-1)(a2-a1)=1),即(n-1),从而

回顾：要用严谨的方法来证明a2018＞1,由数列{an+1-an}是递增数列而获得式子)是关键。这就是用一次(线性)变化(具有单调性)来获得估计目标变化的方法。

方法推广：其实,在解决很多数列问题时,我们要注意该数列可能恒为正数数列,更要注意该数列的差数列{an+1-an}可能是单调数列,或该数列的比数列可能是单调数列。掌握了这样的性质,就可以考虑用一次线性变化,或底数确定的指数变化来估算我们的目标了。

我们可以利用此方法解决下面的跟踪训练题。

跟踪训练：已知数列{an}满足a1=1,

简略分析：仔细观察,可以发现从第2项开始数列的每一项恒大于1,且是递增的,由函数f(x)=x+在x＞2时是递增函数,可以进一步发现该数列的比数列递增的。下面就可由递推式变形进行证明了。