高考推理与证明高分突破

■安徽省阜阳市太和中学 岳 峻

“推理与证明”是数学的基本思维过程,也是人们学习和生活中经常使用的思维方式。推理一般包括合情推理和演绎推理,推理与证明贯穿于高中数学的整个体系,它是新课标教材的一个亮点,是对以前所学知识与方法的总结、归纳,并对同学们的后继学习起到引领的作用。

考点突破一、合情推理

考纲要求：了解合情推理的含义,能进行简单的归纳推理和类比推理,体会并认识合情推理在数学发现中的作用。

权威解读：归纳推理是由某类事物的部分对象具有某些特征,推出该类事物的全部对象都具有这些特征的推理,或者由个别事实概括出一般结论的推理,称为归纳推理(简称归纳)。简而言之,归纳推理是由部分到整体,由个别到一般的推理;类比推理是由两类对象具有某些类似特征和其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理,称为类比推理(简称类比)。归纳推理和类比推理统称为合情推理。

例1 (2016年山东卷)观察下列等式:

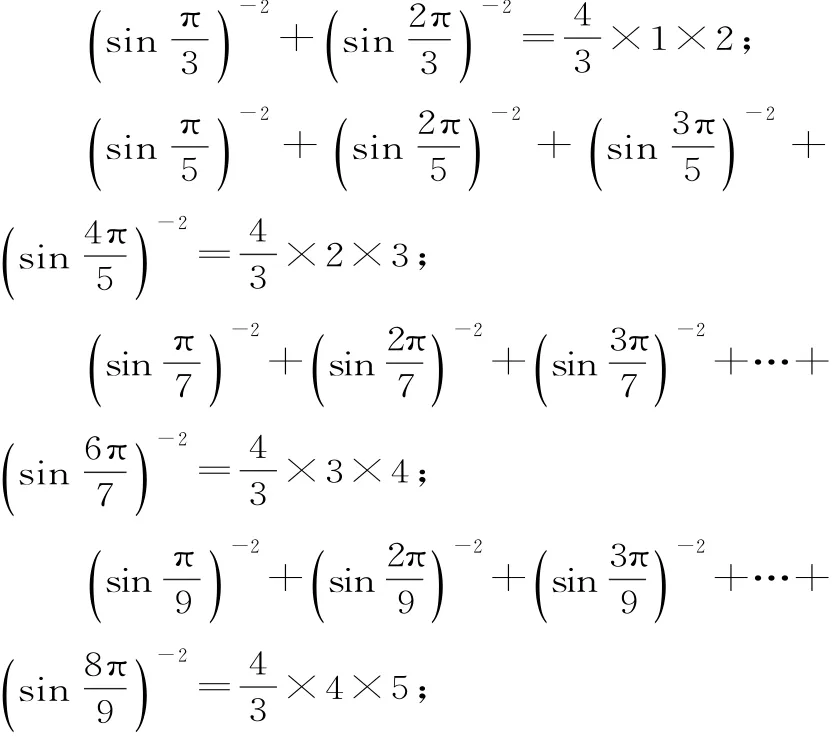
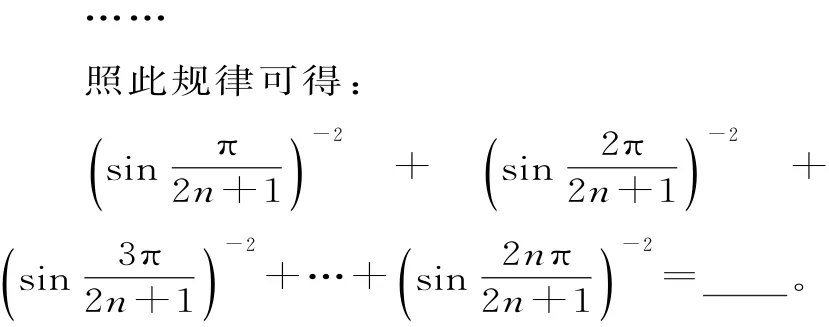
解析：观察易知3=1+2,5=2+3,7=3+4,9=4+5,…,归纳可得2n+1=n+(n+1)。

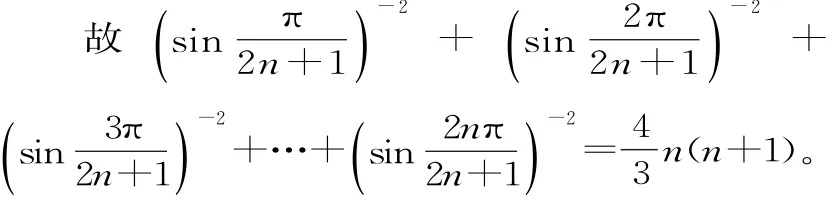
点评:在解决问题的过程中,合情推理具有猜测和发现结论、探索和提供思路的作用,有利于培养同学们的创新意识。

跟踪训练1：(2018届安徽太和中学质量检测)观察以下各等式:

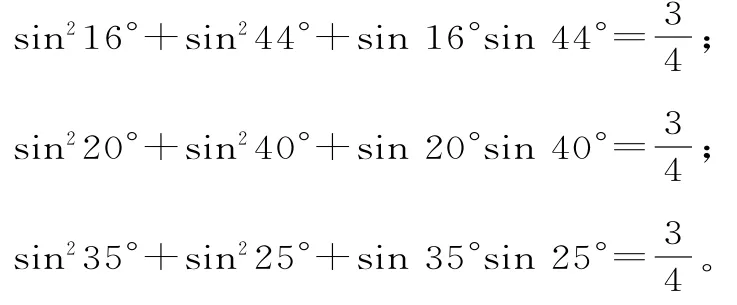
(1)分析上述各式的共同特点,猜想出一般规律的等式;

(2)并借助于正弦定理、余弦定理对等式的正确性给出证明。

提示：(1)设α+β=60°,则sin2α+sin2β+sinαsin

(2)设a,b,c是△ABC的三个内角A,B,C的对应边,若A+B=60°,则:

c2=a2+b2-2abcosC=a2+b2+ab。

又a=2RsinA,b=2RsinB,c=2RsinC,代入上式并化简得:

例2 如图1,P是斜三棱柱ABC-A1B1C1的侧棱BB1上的一点,PM⊥BB1且交AA1于M,PN⊥BB1且交CC1于N。

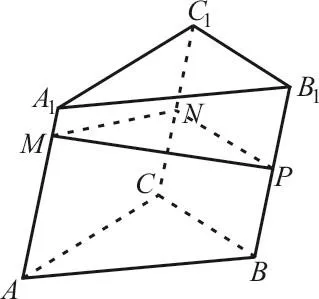
图1

(1)证明:CC1⊥MN;

(2)类比平面几何的余弦定理,写出斜三棱柱ABC-A1B1C1的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并加以证明。

解析：(1)因为PM⊥BB1,PN⊥BB1,并且PN,PM⊂平面MNP,PM∩PN=P,所以BB1⊥平面MNP。

因为MN⊂平面MNP,所以BB1⊥MN。

又因为BB1∥CC1,所以CC1⊥MN。

(2)由题意可知,两个侧面所成的二面角M-BB1-N的平面角为∠MPN。

在△MPN中,MN2=MP2+NP2-2MP·NPcos∠MPN。

两边同乘BB21,化简可得:

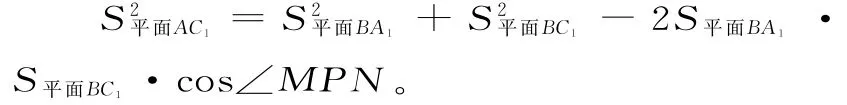
点评:高考中的类比一般包括由数到数的类比、由形到形的类比、论证方法的类比,通过两类事物的类比可以对事物的性质有更深刻的理解。

跟踪训练2：(2018年湖南株洲六校联考)对于问题:“已知关于x的不等式ax2+bx+c＞0的解集为(-1,2),求关于x的不等式ax2-bx+c＞0的解集。”

给出如下一种解法:

由ax2+bx+c＞0的解集为(-1,2),得a(-x)2+b(-x)+c＞0的解集为(-2,1),即关于x的不等式ax2-bx+c＞0的解集为(-2,1)。

故所求不等式的解集为(-3,-1)∪(1,2)。

考点突破二、逻辑推理

考纲要求：了解演绎推理的含义,了解合情推理和演绎推理的联系和差异;掌握演绎推理的“三段论”,能运用“三段论”进行一些简单的演绎推理。

权威解读：演绎推理是根据已有的事实和正确的结论(包括定义、公理、定理等),按照严格的逻辑法则得到新结论的推理过程。培养和提高学生的演绎推理或逻辑证明的能力是高中数学课程的重要目标。

例3 (2016年新课标Ⅱ卷)有三张卡片,分别写有1和2,1和3,2和3。甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2。”乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1。”丙说:“我的卡片上的数字之和不是5。”则甲的卡片上的数字是____。

解析：第一句意味着甲与乙的卡片上相同的数字不是2,等价于丙的卡片不是(1,3),第三句意味着丙的卡片上的数字之和不是5,等价于丙拿的不是(2,3),所以丙拿的是(1,2);第二句意味着乙与丙的卡片上相同的数字不是1,等价于甲的卡片不是(2,3),所以乙的卡片是(2,3),甲的卡片只能是(1,3)。

点评:本题以三个人,三张不同卡片,每人持有一张作为问题的背景,依据三人的陈述,确定三个人各自持有的卡片。本题要求同学们理解所陈述的含义,根据陈述排除不合要求的分配情况,最终确定每个人手中的卡片内容。试题注重考查同学们逻辑思维的基本素养,没有现成的解题套路,但有利于考查同学们独立思考、解决问题的能力。

跟踪训练3:(2017年新课标Ⅱ卷)甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩。老师说:你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩。看后甲对大家说:我还是不知道我的成绩。根据以上信息,判断( )。

A.乙可以知道四人的成绩

B.丁可以知道四人的成绩

C.乙、丁可以知道对方的成绩

D.乙、丁可以知道自己的成绩

提示：由甲的说法可知乙、丙一人优秀一人良好,则甲、丁一人优秀一人良好;乙看到丙的结果则知道自己的结果,丁看到甲的结果则知道自己的结果,故选D。

例4 (2016年北京卷)袋中装有偶数个球,其中红球、黑球各占一半。甲、乙、丙是三个空盒。每次从袋中任意取出两个球,将其中一个球放入甲盒,如果这个球是红球,就将另一个球放入乙盒,否则就放入丙盒。重复上述过程,直到袋中所有球都被放入盒中,则( )。

A.乙盒中黑球不多于丙盒中黑球

B.乙盒中红球与丙盒中黑球一样多

C.乙盒中红球不多于丙盒中红球

D.乙盒中黑球与丙盒中红球一样多

解析：每次从袋中抓出两个球的情形有四种:①红黑;②红红;③黑黑;④黑红。

情形①放入甲盒的是红球,导致乙盒中黑球加1;情形②放入甲盒的是红球,导致乙盒中红球加1;情形③放入甲盒的是黑球,导致丙盒中黑球加1;情形④放入甲盒的是黑球,导致丙盒中红球加1。

不妨设①有a次,②有b次,③有c次,④有d次,则甲盒有红球a+b个,黑球c+d个;乙盒有黑球a个,红球b个;丙盒有黑球c个,红球d个。由于红球、黑球数目相等,所以a+2b+d=a+2c+d,即b=c,故乙盒中红球与丙盒中黑球一样多,所以选B。

点评:上面对球的取放规则进行分析和逻辑推理,环环相扣,准确地把握取放规则的内涵,其突破口是将抽象的取放法则数据化,发现内在规律,进而解决问题。

跟踪训练4:(2017年北京卷)某学习小组由学生和教师组成,人员构成同时满足以下三个条件:

(i)男学生人数多于女学生人数;

(ii)女学生人数多于教师人数;

(iii)教师人数的两倍多于男学生人数。

①若教师人数为4,则女学生人数的最大值为____;

②该小组人数的最小值为____。

①当z=4时,8＞x＞y＞4,所以x的最大值为7,y的最大值为6,故女学生人数的最大值为6。

考点突破三、反证法

考纲要求：了解反证法的思考过程和特点。

权威解读：反证法是间接证明法的一类,是从反方向证明的证明方法,即:肯定题设条件而否定结论,经过推理导出矛盾,从而证明原命题。反证法的逻辑原理是逆否命题和原命题的真假性相同。

(1)求椭圆C的标准方程;

(2)过点F1的直线l1与椭圆C交于M,N两点,过点F2的直线l2与椭圆C交于P,Q两点,且l1∥l2,证明:四边形MNPQ不可能是菱形。

又c2=a2-b2,所以椭圆C的标准方程

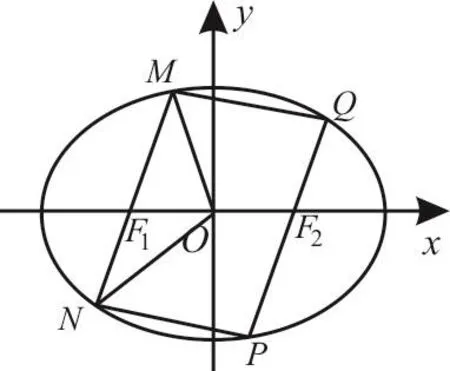
图2

(2)由(1)可知F1(-1,0),如图2,易知直线MN不能平行于x轴,所以令直线MN的方程为x=my-1,M(x1,y1),N(x2,y2)。

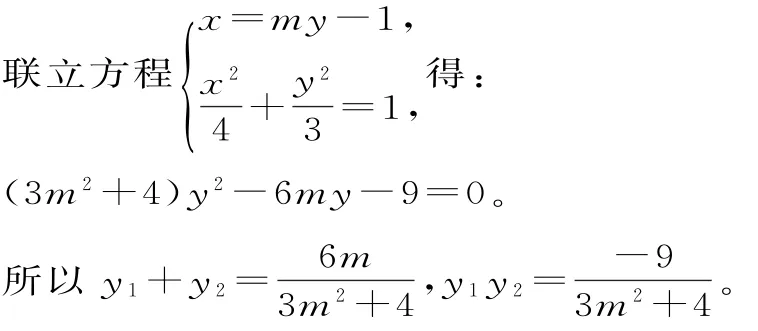
此时|MN|=(1+m2)[(y1+y2)2-4y1y2]。

同理,令直线PQ的方程为x=my+1,P(x3,y3),Q(x4,y4)。

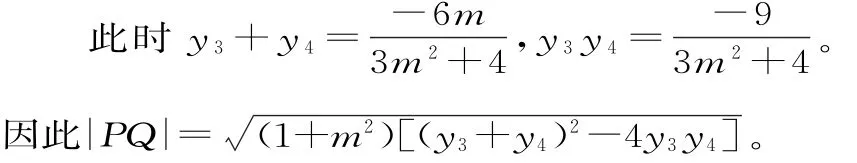
故|MN|=|PQ|,所以四边形MNPQ是平行四边形。

又x1x2=(my1-1)(my2-1)=m2y1y2-m(y1+y2)+1,所以有(m2+1)y1y2-m(y1+y2)+1=0,整理得到即12m2+5=0。

上述关于m的方程显然没有实数解,故四边形MNPQ不可能是菱形。

点评:反证法适宜证明“存在性问题,唯一性问题”,带有“至少有一个”或“至多有一个”等字样的问题,直接证明有困难时,常采用反证法。

跟踪训练5:(2017年德州一模)如果△A1B1C1的三个内角的余弦值分别等于△A2B2C2的三个内角的正弦值,则△A2B2C2是____三角形。(填“锐角”、“直角”或“钝角”)

提示：由条件知,△A1B1C1的三个内角的余弦值均大于0,则△A1B1C1是锐角三角形。

假设△A2B2C2是锐角三角形,则:

那么A2+B2+C2=,这与A+B+C=π相矛盾,所以假222设不成立。

又显然△A2B2C2不是直角三角形,故△A2B2C2是钝角三角形。

跟踪训练6:(2018届阜阳第一次质量检测)已知f(x)=ax2+bx+c,若a+c=0,f(x)在[-1,1]上的最大值为2,最小值为

提示：(1)假设a=0,f(x)=bx,显然b≠0,f(x)在[-1,1]上是单调函数,则f(x)的最大值为|b|,最小值为-|b|,此时|b|+(-|b|)=0,与已知条件相矛盾,所以a≠0。

考点突破四、综合法与分析法

考纲要求：了解直接证明的两种基本方法:综合法和分析法;了解综合法和分析法的思考过程和特点。

权威解读：分析法和综合法是思维方向相反的两种思考方法,当题目从题设不易入手,而从结论上较易打开思路时,多用分析法证明。我们在实际解题时,应把两种方法结合起来运用,先用分析法寻求解题思路,再用综合法有条理地表达解题过程,这就达到了扬长避短、相互协调、相得益彰的目的。

例6 (2017年山东文科卷)由四棱柱ABCD-A1B1C1D1,截去三棱锥C1-B1CD1后得到的几何体如图3所示,四边形ABCD为正方形,O为AC与

BD的交点,E为AD的中点,A1E⊥平面ABCD。

(1)证明:A1O∥平面B1CD1;

(2)设M 是OD的中点,证明:平面A1EM⊥平面B1CD1。

解析：(1)取B1D1中点O1,连接CO1,A1O1,由于ABCD-A1B1C1D1为四棱柱,所以A1O1∥CO,A1O1=CO,因此四边形A1OCO1为平行四边形,A1O∥O1C。

又O1C⊂平面B1CD1,A1O⊄平面B1CD1,所以A1O∥平面B1CD1。

(2)因为AC⊥BD,E,M分别是AD,OD的中点,所以EM⊥BD。因为ABCD为正方形,所以AO⊥BD。又A1E⊥平面ABCD,BD⊂平面ABCD,所以A1E⊥BD。

因为B1D1∥BD,所以A1E⊥B1D1,EM⊥B1D1。

又A1E,EM⊂平面A1EM,A1E∩EM=E,所以B1D1⊥平面A1EM。

又B1D1⊂平面B1CD1,所以平面A1EM⊥平面B1CD1。

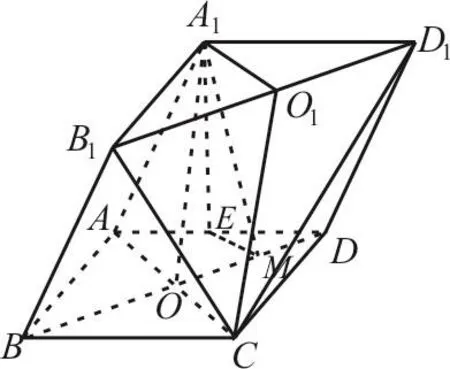
图3

点评:综合法是利用已知条件和某些数学定义、定理、公理等,经过一系列的推理证明,最后推导出所要证明的结论成立,这种证明方法叫作综合法,又叫顺推证法。它的基本思路是“由因导果”。

(1)求M;

(2)证明:当a,b∈M时,|a+b|＜|1+ab|。

综上可得,M={x|-1＜x＜1}。

(2)当a,b∈(-1,1)时,有(a2-1)·(b2-1)＞0,即a2b2+1＞a2+b2。

则a2b2+2ab+1＞a2+2ab+b2。

整理得(ab+1)2＞(a+b)2,故|a+b|＜|ab+1|。

例7 (2017年全国Ⅱ卷)已知a＞0,b＞0,a3+b3=2,证明:

(1)(a+b)(a5+b5)≥4;

(2)a+b≤2。

解析：(1)(a+b)(a5+b5)=a6+ab5+a5b+b6=(a3+b3)2-2a3b3+ab(a4+b4)

=4+ab(a2-b2)2≥4。

(2)因为a＞0,b＞0,所以要证明a+b≤2,只需证明(a+b)3≤8,也即证明a3+3a2b+3ab2+b3≤8。

而a3+b3=2,只需证明a2b+ab2≤2。

而a2b+ab2-2=a2b+ab2-a3-b3=a2(b-a)-b2(b-a)=(a2-b2)(b-a)=-(b-a)2(b+a)≤0,此式显然成立,故a+b≤2。

点评:分析法是从待证明的结论出发,从“未知”看“需知”,渐渐靠拢“已知”,逐步寻找使它成立的充分条件,直至最后把要证明的结论归结为判定一个明显成立的条件,这种证明方法叫分析法。它的基本思路是“执果索因”。

因为a⊥b,所以a·b=0。只需证明|a|2+|b|2-2|a||b|≥0,即(|a|-|b|)2≥0,得证。

考点突破五、数学归纳法

考纲要求：了解数学归纳法的原理,能用数学归纳法证明一些简单的数学命题。

权威解读：当遇到与正整数n有关的不等式证明时,应用其他办法不容易证明,则可考虑应用数学归纳法证明。利用数学归纳法可以探索与正整数n有关的未知问题、存在性问题,其基本模式是“归纳—猜想—证明”,即先由合情推理发现结论,然后经逻辑推理即演绎推理论证结论的正确性。

例8 (2017年浙江卷)已知数列{xn}满足:x1=1,xn=xn+1+ln(1+xn+1),n∈N*。

证明:当n∈N*时,

(1)0＜xn+1＜xn;

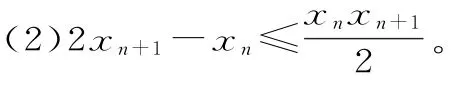
解析：(1)用数学归纳法证明xn＞0。

当n=1时,x1=1＞0。

假设n=k时,xk＞0。

那么n=k+1时,若xk+1≤0,则0＜xk=xk+1+ln(1+xk+1)≤0,矛盾,故xk+1＞0。

因此xn＞0,n∈N*。

因为xn=xn+1+ln(1+xn+1),因此0＜xn+1＜xn,n∈N*。

(2)由xn=xn+1+ln(1+xn+1)得:

xnxn+1-4xn+1+2xn=xn2+1-2xn+1+(xn+1+2)·ln(1+xn+1)。

记函数f(x)=x2-2x+(x+2)ln(1+x)(x＞0)。

所以函数f(x)在(0,+∞)上单调递增。

因此f(x)＞f(0)=0,xn2+1-2xn+1+(xn+1+2)ln(1+xn+1)=f(xn+1)≥0。

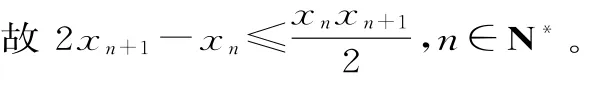
点评:应用数学归纳法证明不等式的关键是由n=k成立,证明n=k+1时也成立,证明时用归纳假设后,可采用分析法、综合法、求差(求商)比较法、放缩法等证明。

跟踪训练9:(2018届莱芜实验中学模拟)已知数列{an}的前n项和Sn满足Sn=(1)求a1,a2,a3的值;(2)求{an}的通项公式。

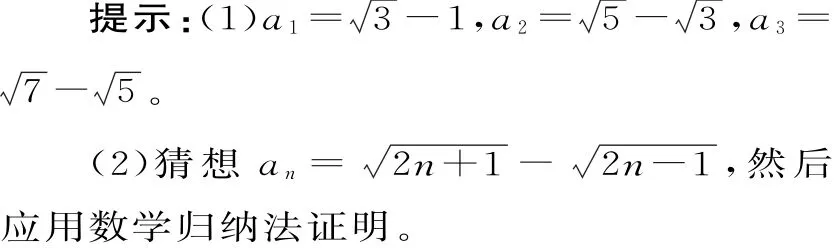
考点突破六、放缩法

考纲要求：了解放缩法的原理,能用放缩法证明一些简单的数学命题。

权威解读：放缩法是不等式证明中最重要的方法之一,放缩必须有目标,而且要恰到好处,目标往往要从证明的结论考查。常用的放缩方法有增项、减项,可利用分式的性质、不等式的性质、已知不等式,以及函数的性质进行放缩等。

例9 (2018届成都七中月考)函数f(x)=ex-2ax,g(x)=ax2+1(a∈R)。

(1)设函数h(x)=g(x)-f(x),其导函数为h'(x),若h'(x)在[0,+∞)上具有单调性,求a的取值范围;

解析：(1)h(x)=ax2+2ax-ex+1,h'(x)=2ax+2a-ex。

设u(x)=h'(x)=2ax+2a-ex,u'(x)=2a-ex。

若u'(x)=2a-ex≤0在[0,+∞)上恒成立,即2a≤ex在[0,+∞)上恒成立,则a≤

1;2

若u'(x)=2a-ex≥0在[0,+∞)上恒成立,即2a≥ex在[0,+∞)上恒成立,此时ex∈[1,+∞),故不存在a使得2a≥ex在[0,+∞)上恒成立。

所以h(x)在(0,+∞)上单调递减,h(x)＜h(0)=0,即ex-x＞

点评:在放缩法证明不等式的过程中,往往采用添项或减项的方法,放缩时要注意适度,否则不能同向传递。

跟踪训练10:(2016年四川卷)已知数列{an}的首项为1,Sn为数列{an}的前n项和,Sn+1=qSn+1,其中q＞0,n∈N*。

(1)若2a2,a3,a2+2成等差数列,求数列{an}的通项公式;

提示：(1)因为Sn+1=qSn+1,所以n≥2时,Sn=qSn-1+1。

两式相减可得an+1=qan,即从第二项开始,数列{an}为等比数列,公比为q。

当n=1时,a1+a2=S2=qa1+1。

由于a1=1,a2=a1q=q,又2a2,a3,a2+2成等差数列,则2q+q+2=2q2,解得q=2或q=-