行走在复数创新的路上

■江苏省张家港职业教育中心校 韩文美

数学思维的创新是思维品质的最高层次,每年的新课标高考,都会出现一些考查创新知识或能力的数学问题。复数在新课程标准下成为文、理科选修中的共同部分,在知识掌握程度上要求偏低一些,一般以选择题或填空题的形式出现在考题中,由于其自身的诸多特点,成为数学创新中的一道亮丽的风景线。

1.定义创新

此类复数创新问题往往设计一个全新的数学情境,采用定义新概念的形式出现,背景新颖,构造巧妙,可以非常有效地考查知识迁移能力。

例1 定义:复数b+ai是复数z=a+bi(a,b∈R)的转置复数,记为z*=b+ai。给出下列四个命题:

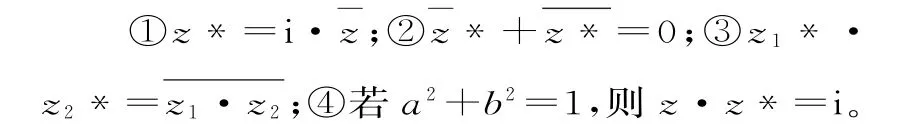
其中真命题的个数为 个___。

分析：根据创新定义的转置复数的新概念,结合共轭复数定义以及复数的四则运算法则加以分析,判断对应的命题的真假。

解：由于i·z=i(a-bi)=ai+b=z*,①正确。

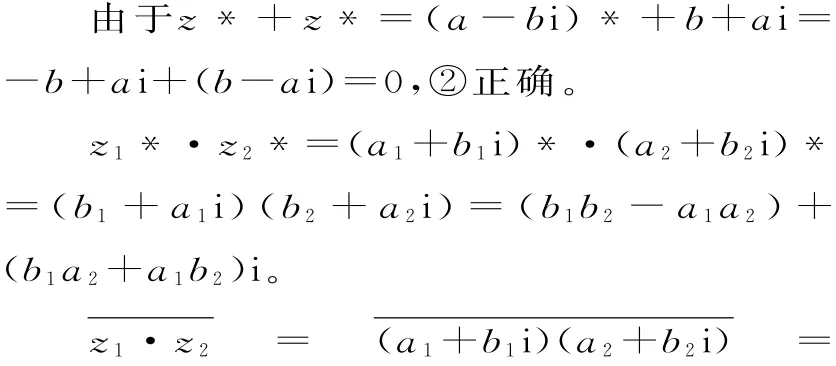
由于a2+b2=1,则z·z*=(a+bi)(b+ai)=a2i+b2i=(a2+b2)i=i,④正确。

故真命题的个数为3。

点评:此类问题是根据创新的新定义,在理解转置复数z*的意义的基础上,利用复数的共轭复数以及复数的四则运算加以应用。解决此类定义创新问题,关键是对信息的收集、加工和运用,将新定义与已学过的知识联系在一起运用。

2.运算创新

此类复数创新问题往往通过约定一种新运算,创设一种全新的问题情境,要求在新运算的基础上,紧扣条件,抓住关键的运算信息,实际信息的转化与解决,达到灵活解题的目的。

分析：根据复数模的定义先确定复数z1、z2的模,再结合创新运算计算出z1☉z2的值,进而再结合运算结果与创新运算进行运算求解。

解：根据复数模的定义,知|z1|=

则有|z1|＜|z2|。根据题中“☉”的运算法则,可得:

z1☉z2=(3+i)-(2+3i)=1-2i。

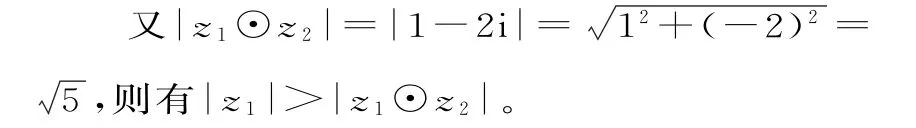
根据题中的定义运算“☉”的运算法则,可得:

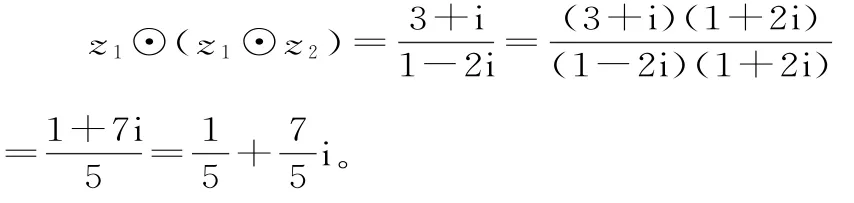
点评:此类问题是根据创新的新运算,自主运用此运算法则解决问题。这类题在各类考试中层出不穷,难度不大,背景新颖,主要考查同学们自主学习新运算的能力,以及阅读理解能力和运算求解能力。

3.关系创新

此类复数创新问题往往通过定义一种全新的复数关系,以一个陌生的问题背景,在新关系的基础上利用复数的相关概念或四则运算来处理相关的数学问题,知识交汇性强,考查同学们综合应用知识解决问题的能力。

例3 定义:对于复数z1与z2,叫作复数的模平均,记作z※z12若复数z=a+bi(a,b∈R),且满足a+b=4,则z※z的最小值为_____。

分析：根据创新关系得到z※z的关系式,结合条件a+b=4,可通过二次函数的图像与性质来求解相应的最值问题。

解：由于z=a+bi(a,b∈R),那么z=a-bi。

而a+b=4,那么把b=4-a代入,可得:

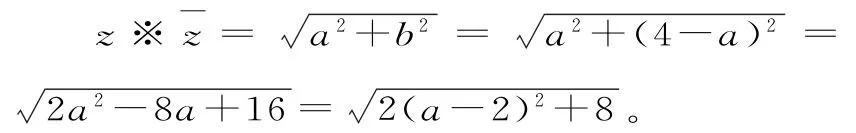
点评:解决此类问题的关键是正确理解创新定义,利用创新关系,把复数问题转化为相应根式下含有的二次函数问题,利用配方法来解决二次函数相应的最值问题。

4.方法创新

此类复数创新问题往往结合问题背景,通过其他知识中的一些创新方法来处理复数背景下的问题,往往可以类比函数、不等式、数列、平面向量等知识中的相关方法来处理对应的复数问题,达到创新应用的目的。

例4 计算:1+2i+3i2+4i3+…+2018i2017=____。

分析：直接利用复数的虚数单位i的性质来求解,比较烦琐且不好化简,而结合复数关系式的性质,类比等比数列的“错位相减法”求和方法来处理,可以很好地解决问题。

解：设S=1+2i+3i2+4i3+…+2018i2017。

则iS=i+2i2+3i3+4i4+…+2018i2018。

两式对应相减,可得:

(1-i)S=1+i+i2+i3+i4+…+i2017-2018i2018

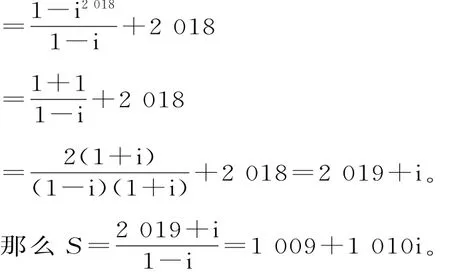
点评:结合复数的关系式,类比等比数列的求和方法——错位相减法,利用等比数列的前n项和公式以及复数的四则运算加以转化,方法创新,技巧性强,可以大大简化计算过程,提高解题效益。

在强化能力立意的新课标高考思维下,不断提升创新发展理念,创新试题必然会不断出现。行走在复数创新的路上,必有创新的收获,这类复数创新问题大都是按照复数的相关规则和要求,结合复数的相关知识加以创新,进行逻辑推理和计算,从而达到解决复数创新问题的目的。