极值点偏移问题的解题探析
■甘肃省白银市第一中学 胡贵平
极值点偏移问题,是指单极值函数由于函数极值点左右两边的增减速度不同,使得函数图像没有对称性。若函数f(x)在x=x0处取得极值,且函数y=f(x)与直线y=b交于A(x1,b),B(x2,b)两点,则AB的中点为M
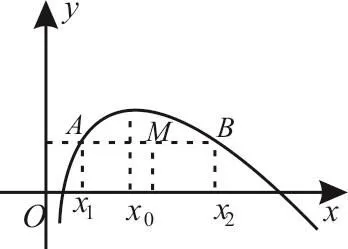
图1
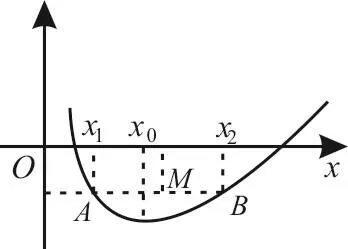
图2
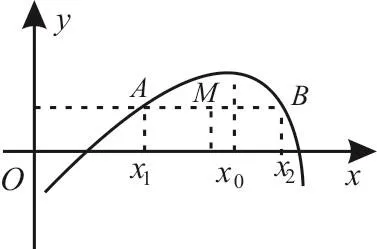
图3

图4
极值点偏移问题涉及函数的双变元,最常见的题型是两个变元的不等式证明,或有关导函数值的不等式,解题的策略都是把双变元的等式或不等式转化为单变元的问题求解,途径都是构造一元函数。
(1)求实数a,b的值及函数f(x)的单调区间;
(2)当f(x1)=f(x2)(x1≠x2)时,比较x1+x2与2e(e为自然对数的底数)的大小。
因为f(x)的图像在点(1,f(1))处的切线方程为y=x-1,所以
解得a=1,b=0。
令f'(x)=0,得x=e。
当0<x<e时,f'(x)>0,f(x)单调递增;当x>e时,f'(x)<0,f(x)单调递减。
所以函数f(x)的单调递增区间为(0,e),单调递减区间为(e,+∞)。
(2)当f(x1)=f(x2)(x1≠x2)时,x1+x2>2e。证明如下:
当1≤x<e时,f(x)单调递增,且f(1)=0,故f(x)>0。
若f(x1)=f(x2)(x1≠x2),则x1,x2必都大于1,且必有一个小于e,一个大于e。
不妨设1<x1<e<x2。
当x2≥2e时,必有x1+x2>2e。
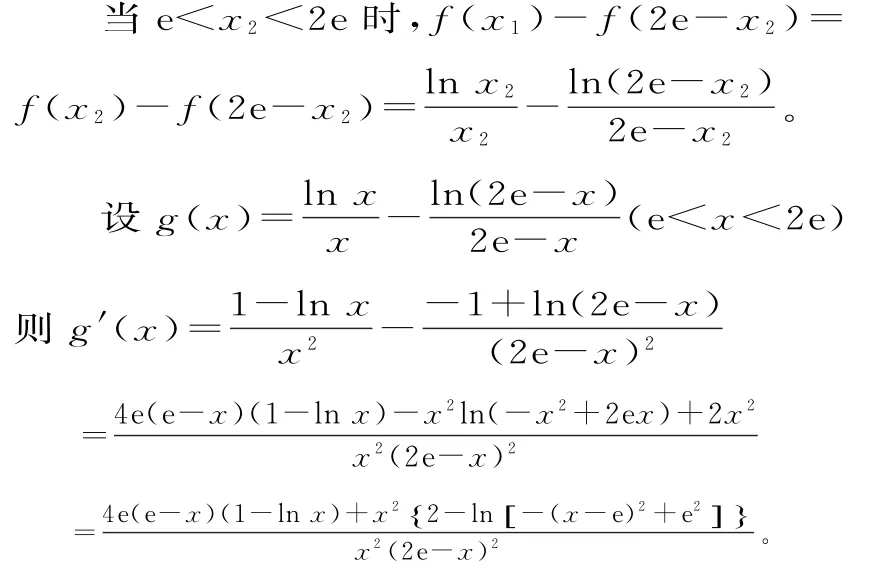
因为e<x<2e,所以e2-(x-e)2的取值范围为(0,e2)。
故2-ln[-(x-e)2+e2]>0。
又4e(e-x)(1-lnx)>0,所以g'(x)>0。
因此,g(x)在区间(e,2e)上单调递增。
因为1<x1<e,e<x2<2e,所以0<2e-x2<e。
又因为f(x)在区间(0,e)内单调递增,所以x1>2e-x2,则x1+x2>2e。
综上,当f(x1)=f(x2)(x1≠x2)时,x1+x2>2e。
点评:为了实现将双变元的不等式转化为单变元不等式,需要构造新的函数。也可以利用f(x1)=f(x2)(x1≠x2)构造新的变元,将两个旧的变元都换成新变元来表示,从而达到消元的目的。
此类问题常见的解题步骤:
(1)讨论函数f(x)的单调性,并求出f(x)的极值点x0;
(2)构造g(x)=f(x0+x)-f(x0-x)(根据题意需要还可以构造成g(x)=f(x)-f(2x0-x)的形式);
(3)通过求导函数g'(x),讨论g(x)的单调性,判断出g(x)在某段区间上的正负,并得出f(x0+x)与f(x0-x)的大小关系;
(4)不妨设x1<x0<x2,通过f(x)的单调性,f(x1)=f(x2),f(x0+x)与f(x0-x)的大小关系得出结论。
(1)讨论f(x)的单调性;
(2)设a>0,证明:当0<x<a时,f(a+x)<f(a-x);
(3)设x1,x2是f(x)的两个零点,证明
分析:本题涉及利用导数研究函数的单调性、根的存在性及根的个数判断。
(1)求出函数的导数,通过讨论a的取值范围,求出函数的单调性即可;
(2)令g(x)=f(a+x)-f(a-x),求出函数的导数,得到函数的单调区间,从而证出结论即可;
(3)得到a>0,从而f(x)的最小值是f(a),且f(a)<0,不妨设0<x1<x2,则0<x1<a<x2,得到0<a-x1<a,根据(1),(2)结论判断即可。
解:(1)f(x)的定义域为(0,+∞)。
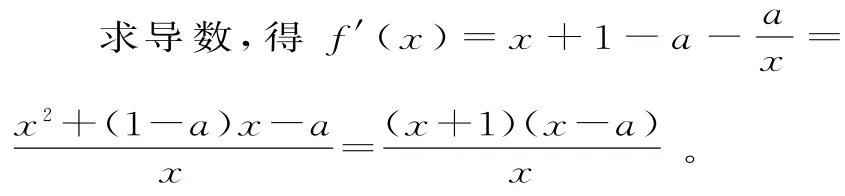
若a≤0,则f'(x)>0,此时f(x)在(0,+∞)上单调递增。
若a>0,则由f'(x)=0得x=a。
当0<x<a时,f'(x)<0;
当x>a时,f'(x)>0。
此时f(x)在(0,a)上单调递减,在(a,+∞)上单调递增。
(2)令g(x)=f(a+x)-f(a-x),则:

当0<x<a时,g'(x)<0,g(x)在(0,a)上是减函数。
而g(0)=0,g(x)<g(0)=0。
当0<x<a时,f(a+x)<f(a-x)。
(3)由(1)可知,当a≤0时,函数y=f(x)至多有一个零点,故a>0,从而f(x)的最小值为f(a),且f(a)<0。
不妨设0<x1<x2,则0<x1<a<x2,0<a-x1<a。
由(2)得f(2a-x1)=f(a+a-x1)<f(x1)=f(x2)=0。

点评:本题考查了利用导数研究函数的单调性,以及分类讨论思想恒成立问题中的等价转化思想,属于难题。
极值点左偏,x1+x2>2x0处切线不平行于x轴,若f(x)是上凸函数,f'(x)是减函数,则0;若f(x)是下凸函数,f'(x)是增函数,则
极值点偏移问题变化多样,有些题型是不含参数的,而更多的题型是含有参数的。含参数的极值点偏移问题,在原有的两个变元x1,x2的基础上,又多了一个参数,故思路很自然地就会想到:想尽一切办法消去参数,从而转化成不含参数的问题去解决;或者以参数为媒介,构造出一个变元的新的函数,其实,处理的手段有很多,方法也就有很多。

