基于UPF的车辆紧耦合定位算法*

蒋 荣，陈 柏

(1.东南大学 仪器科学与工程学院，江苏 南京210096；2.南京航空航天大学 机电学院，江苏 南京210016)

0 引 言

随着智能交通系统(intelligent transportation system，ITS)的高速发展，高精度和高可靠性定位系统在智能车辆相关应用中受到了广泛地关注，例如驾驶辅助系统、防碰撞预警系统和交通控制等[1-3]。目前，作为主流定位系统，组合导航系统融合了多种优势互补的传感器信息，能有效提高定位精度，被广泛应用于车辆导航定位领域。其中，比较常用的多传感器融合方式是全球卫星导航系统(GNSS)和惯性导航系统(INS)的融合。

全球卫星导航系统作为车辆定位的主要信息来源，近年来发展迅速。除了GPS外，中国的北斗(BeiDou)、俄罗斯的格洛纳斯(GLONASS)以及欧洲的伽利略(GALILEO)等卫星导航系统都逐渐成熟。相对于单一模式的GNSS，多模GNSS在卫星的几何分布和卫星数量上，均有着较大的优势，即使在复杂的城市环境下，仍有较多的卫星可用于定位解算。因此，多模GNSS被越来越多地应用到车辆组合导航定位中[4-5]。但是卫星导航系统也有局限性，例如在峡谷、隧道等遮挡环境下无法提供精确的导航定位。相比而言，惯性导航系统(INS)由加速度计和陀螺仪组成，它能够完全依赖设备自身完成导航定位，工作时不受外界的影响。但其定位误差会随着时间不断累积，从而导致定位精度和可靠性下降。然而，高精度的全维惯性单元因为成本较高并不适用于车辆导航领域。因此如何实现稳定、精确且低成本的车辆导航定位已成为研究的热点[6-7]。

此外，对于INS/GNSS非线性组合导航系统而言，基于序贯蒙特卡洛方法和递推贝叶斯估计的粒子滤波算法(Particle FilterPF)，由于其相比卡尔曼滤波、扩展卡尔曼滤波等具有较强的处理非线性、非高斯系统的能力，已经被广泛地用来实现组合导航中的多传感器信息融合。但是，传统的粒子滤波也存在缺点，例如：粒子贫瘠和退化现象等，尤其是在INS/GNSS组合导航应用中，传统的粒子滤波选择先验概率密度作为重要性密度，而没有考虑到当前的观测值。这样仅仅依赖先验概率密度分布的粒子群会与真实的后验概率密度分布产生很大的偏差，影响定位精度[8-10]。

针对上述问题，本文提出一种基于无迹粒子滤波(UPF)的车辆紧耦合定位算法。

1 非线性系统模型

1.1 状态模型

本文基于降维惯性导航系统(RISS)来设计车辆非线性运动模型。通常组合导航中使用的全维惯性单元包含3个陀螺仪和3个加速度计，这是造成车辆组合导航定位成本高的主要原因。而本文使用的降维惯性导航系统只使用一个垂直方向陀螺仪和两个水平方向的加速度计以及轮速传感器。虽然是降维惯导，但通过陀螺仪估计车辆的航向角，两个加速度计估计车辆的俯仰角和侧倾角，同时再结合轮速传感器信息便仍能够实现三维定位[11]。在本文中，横向加速度、纵向加速度和轮速等信息都可通过车身CAN总线从汽车自带的传感器中获取，节约了成本。

系统状态方程如下：

Xk=f(Xx-1,Uk-1,Wk-1,Tk-1)

(1)

式中：X—系统状态向量；U—系统输入向量；f(·)—非线性状态转移方程；W—系统噪声矩阵；T—输入噪声矩阵。

在INS/GNSS组合导航中，系统噪声和输入噪声通常设置为零均值的高斯噪声，其协方差阵分别是Q和Γ。

系统输入量由加速度计，垂直方向陀螺仪和轮速传感器的信息组成，系统输入向量如下：

U=[vwawfxfyωz]T

(2)

式中：vw—通过轮速测得的车辆速度；aw—从车辆轮速求出的车辆加速度；fx—横向加速度测量值；fy—纵向加速度测量值；ωz—垂直方向陀螺仪输出的横摆角速度。

系统状态向量包括车辆的位置、速度、姿态，如下所示：

X=[φλhvEvNvUprA]T

(3)

式中：φ—纬度信息；λ—经度信息；h—高度信息；vE—车辆的东向速度；vN—车辆的北向速度；vU—车辆的垂向速度；p—车辆的俯仰角；r—车辆的侧倾角；A—车辆的航向角。

根据上文所提的RISS定位模型，可得状态方程具体如下：

(4)

式中：RM—地球子午线曲率半径；RN—正常的地球曲率半径；ωe—地球自转角速度；g—重力加速度。

1.2 观测模型

在紧耦合算法中，多模卫星的伪距信息被用来作为观测向量。

观测方程如下：

Zk=h(Xk)+εk

(5)

式中：Z—观测向量；h(·)—观测方程；ε—观测噪声矩阵。

同样，观测噪声也被认为是零均值的高斯噪声，其协方差阵为R。

在本文提出的紧耦合定位算法中，采用GPS/北斗双模卫星导航系统的伪距测量值作为观测量。观测向量如下：

Z=[ρGPS,1...ρGPS,m1ρBDS,1...ρBDS,m2]T

(6)

式中：ρGPS,ρBDS—指校正过对流层误差和电离层误差的GPS和北斗卫星伪距；m1,m2—各时刻接收到的GPS和北斗卫星数目。

根据卫星伪距定位原理，可得具体的观测方程如下：

(7)

式中：[xyz]—接收机(车辆)的位置；[xGPSyGPS

zGPS]—接收到的GPS卫星位置；[xBDSyBDSzBDS]—接收到的北斗卫星位置；δbGPS,δbBDS—GPS和北斗接收机钟差；e—地球椭圆离心率。

北斗和GPS的卫星位置可以根据双模接收机接受到的各自的星历数据解算获得。

2 信息融合算法

2.1 粒子滤波

系统状态模型和观测模型都是非线性的。粒子滤波(PF)因为能较好地处理非线性、非高斯系统，被广泛地运用在INS/GNSS多传感器信息融合中。粒子滤波算法主要有以下几个步骤[12]：

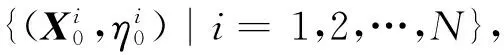
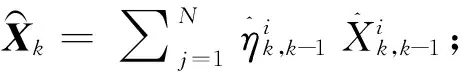
2.2 改进UPF

2.2.1 无迹粒子滤波

UPF的算法由以下几部分组成：

(1)初始化：

(8)

分散粒子：

(9)

(10)

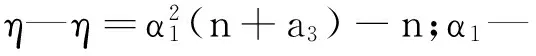
时间更新：

(11)

(12)

测量更新：

(13)

(14)

(15)

(3)更新粒子权重并归一化处理：

(16)

(4)状态估计：

(17)

(5)重采样：

(18)

2.2.2 模糊算法

通常，在INS/GNSS的组合导航算法中，每个卫星伪距的观测噪声都被认为是具有相同噪声协方差阵的高斯噪声。因此，公式(13)中的观测噪声协方差阵通常被设置为：

(19)

为了更好地适应车辆导航环境，提高定位精度，本文的融合算法中采用了一种模糊算法，依据卫星信号的高度角和载波信噪比(C/N0)Pi来对观测噪声协方差阵进行自适应调整[14-15]。

通过先验性知识可以知道：卫星高度角越大的卫星，其信号受周围建筑物和树木的影响会越小，精度相对要高；同时卫星信号的载波信噪比也是评估卫星信号精度的特性之一，精度高的卫星信号，载波信噪比相对较小。依据上面的分析，本文所设计的模糊算法以卫星高度角和载波信噪比作为两个输入量。模糊输出量为调整系数。

该模糊逻辑的输入量、输出量的隶属度函数如图1所示。

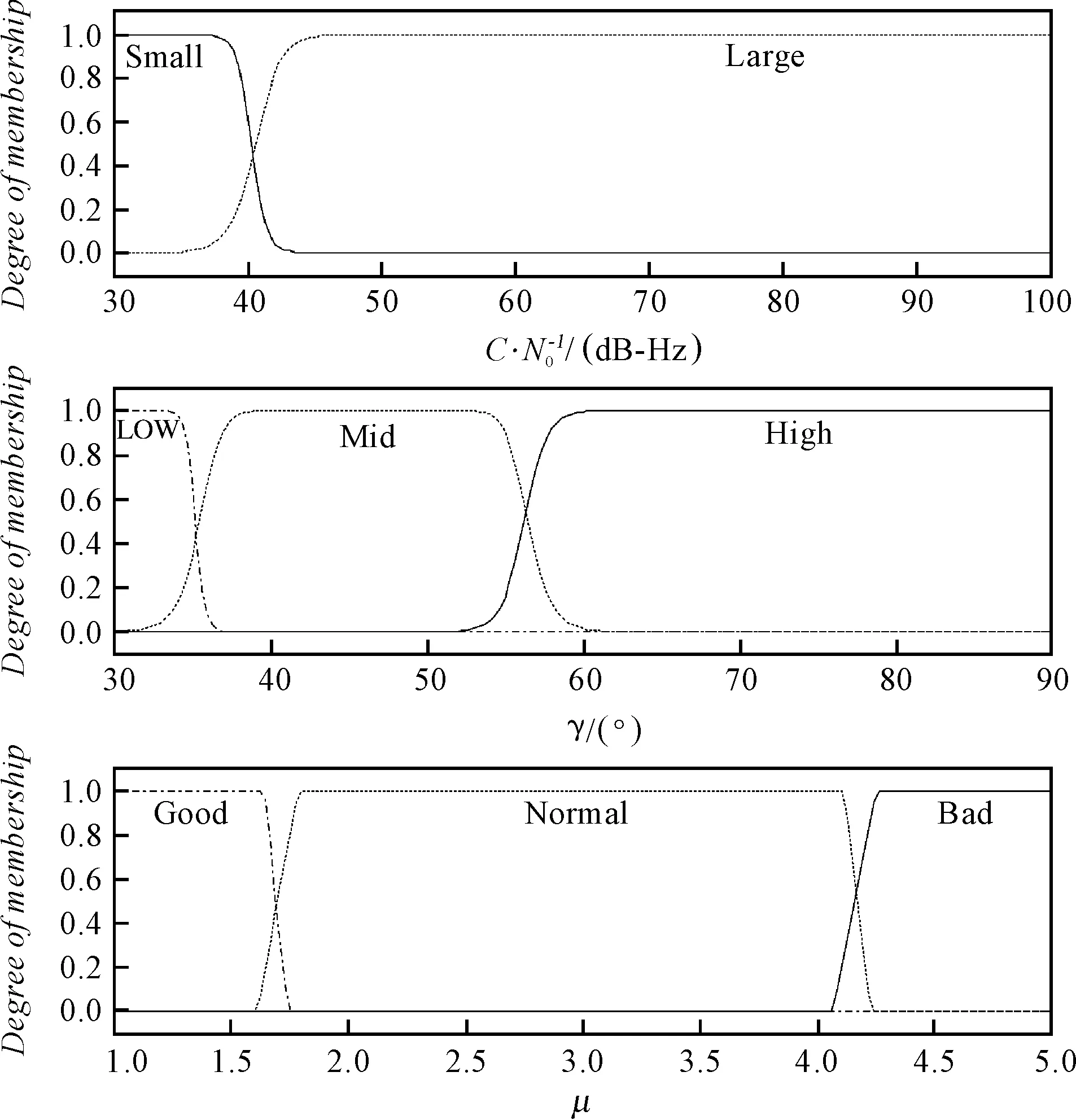
图1 模糊输入、输出隶属度函数

其中，高(High)、中(Mid)、低(Low)3个隶属度函数描述输入特征量高度角；大(Large)和小(Small)两个隶属度函数描述输入特征量载波信噪比；精度好(Good)、精度一般(Normal)、精度差(Bad)3个隶属度函数描述输出变量。

该模糊算法的模糊规则如表1所示。

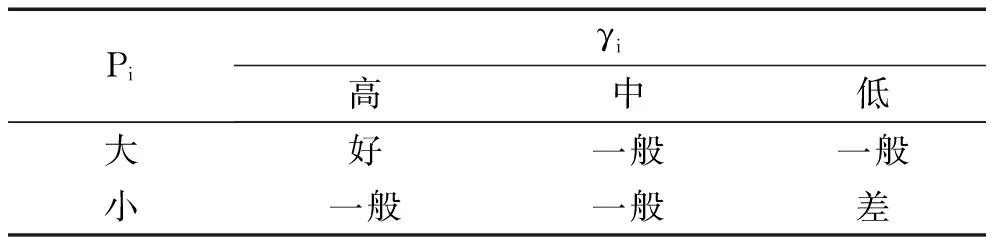
表1 模糊规则

高度高、信噪比大的卫星信号精度最好；高度低、信噪比小的卫星信号精度最差。因此，本文方法中的观测噪声协方差阵可以设置为：

Rk=diag[(μ1R0)2... (μm1+m2R0)2]

(20)

3 实 验

实验中横向和纵向加速度以及轮速信息可直接从车身CAN总线上获取。同时，使用了低成本的GPS/北斗双模卫星接收机NovAtel-C260-AT和MEMS陀螺仪VG440CA-200。此外，NovAtel SPAN-CPT组合导航系统被用来提供参考值。

本文将其与基于PF算法来进行信息融合的定位方法进行了对比，结果如图2所示。

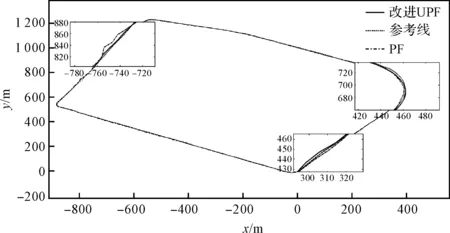
图2 定位结果示意图黑色虚线—SPAN-CPT系统输出的参考值；黑色实线—改进UPF算法的定位结果；黑色点画线—PF算法的定位结果

图2展示的是局部切平面坐标系下的定位结果，横坐标表示车辆东向位置x，纵坐标表示车辆北向位置y。通过对比可以看出，改进UPF和PF都能实现连续的车辆定位，但UPF的定位精度要优于PF。

两种方法定位结果的水平位置误差的统计数据如表2所示。

表2 水平位置误差统计结果

从表2中可以得出，本文所用的改进UPF算法的水平位置误差分别改善了29.46%和21.88%。

两种方法定位误差比较如图3所示。

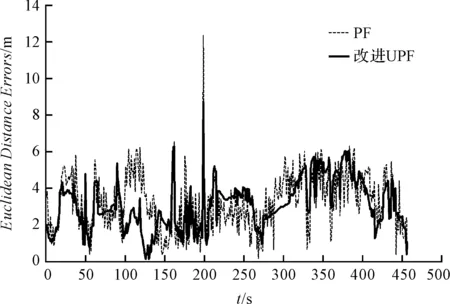
图3 水平位置误差对比图黑色虚线—PF的定位误差；黑色实线—改进UPF的定位误差。

结合表2和图3可知：相比PF算法，本文所使用的算法在定位精度和稳定性上都有明显改善

4 结束语

本文融合双模卫星定位系统和其他低成本车载传感器信息，提出了一种基于UPF的车辆紧耦合定位算法。首先基于降维惯性导航系统(RISS)和双模卫星导航系统建立系统模型；然后使用UPF算法实现多传感器信息融合；此外还运用一种模糊算法对伪距观测噪声协方差值进行自适应调整，从而提高了定位精度。

最后实车实验结果表明：相比基于PF的定位算法，本文方法定位误差的最大值和均方根值分别能改善29.46%和21.88%。因此，本文方法能有效提高车辆定位精度和稳定性，同时还能降低定位成本。

参考文献(References):

[1] VU A, RAMANANDAN A, CHEN A, et al. Real-time computer vision/DGPS-aided inertial navigation system for lane-level vehicle navigation[J].IEEETransactionsonIntelligentTransportationSystems,2012,13(2):899-913.

[2] JO K, CHU K, SUNWOO M. Interacting multiple model filter-based sensor fusion of GPS with in-vehicle sensors for real-time vehicle positioning[J].IEEETransactionsonIntelligentTransportationSystems,2012,13(1):329-343.

[3] SKOG I, HANDEL P. In-car positioning and navigation technologies—a survey[J].IEEETransactionsonIntelligentTransportationSystems,2009,10(1):4-21.

[4] 谢 钢.全球导航卫星系统原理[M].北京:电子工业出版社,2013.

[5] LI X, GE M, DAI X, et al. Accuracy and reliability of multi-GNSS real-time precise positioning: GPS, GLONASS, BeiDou, and Galileo[J].JournalofGeodesy,2015,89(6):607-635.

[7] GEORGY J, NOURELDIN A, KORENBERG M J, et al. Modeling the stochastic drift of a MEMS-based gyroscope in gyro/odometer/GPS integrated navigation[J].IEEETransactionsonIntelligentTransportationSystems,2010,11(4):856-872.

[8] ZHANG D, FU K, GE S S, et al. Analysis of filtering methods for the SINS/CNS integrated navigation system of missile motion[C]. 2014 11th World Congress on Intelligent Control and Automation, Shenyang: IEEE,2014.

[9] YIN S, ZHU X. Intelligent particle filter and its application to fault detection of nonlinear system[J].IEEETransactionsonIndustrialElectronics,2015,62(6):3852-3861.

[10] CHEN X, SHEN C, ZHAO Y. Study on GPS/INS system using novel filtering methods for vessel attitude determination[J].MathematicalProblemsinEngineering,2013(3):289-325.

[11] NOURELDIN A, KARAMAT T B, GEORGY J. Fundamentals of inertial navigation, satellite-based positioning and their integration[M]. Berlin: Springer Science &Business Media,2012.

[12] GEORGY J, KARAMAT T, IQBAL U, et al. Enhanced MEMS-IMU/odometer/GPS integration using mixture particle filter[J].GPSsolutions,2011,15(3):239-252.

[13] 朱志宇.粒子滤波算法及其应用[M].北京：科学出版社,2010.

[14] 王 宇.基于车内总线的车辆双模卫星融合定位技术研究[D].南京：东南大学仪器科学与工程学院,2016.

[15] LI X, JIANG R, SONG X, et al. A tightly coupled positioning solution for land vehicles in urban canyons[J].JournalofSensors,2017(3)：1-11.