高速铁路救援起重机多支撑机构力学解算研究*

刘 永，李 扬，张雷雷*，赵延治，刘康荣，王渊明，于跃斌

(1.中车齐齐哈尔车辆有限公司 大连研发中心 ,辽宁 大连 116052；2.燕山大学 机械工程学院，河北 秦皇岛 066004；3.武汉铁路局 机务处，湖北 武汉 430071；4.秦皇岛烟草机械有限公司，河北 秦皇岛 066004；5.中车齐齐哈尔车辆有限公司，黑龙江 齐齐哈尔 161002)

0 引 言

高速铁路为人们提供方便快捷的同时，也为铁路救援提出了新的课题。高铁线路桥线比大[1]，救援的关键问题是解决桥梁、线路承载能力的限制。现有国内外铁路起重机下车结构主要采用4支腿的结构形式，由于高铁桥梁承载能力的限制，不仅单个支腿所能够承受的最大载荷较地面作业大为降低，此外也对作业起重机多个支腿间载荷均布的程度提出了较高的要求。倘若依然沿用原有结构形式的普通铁路救援起重机，会带来巨大的安全隐患。德国的GOTTWALD公司发明的旋转式伸缩平衡重技术是铁路救援起重机的一重大进步，该公司的产品在瑞士、日本、韩国等市场上占有率高[2]。

为此，一种多支撑系统被提了出来。该系统在原有起重机4支腿支撑的基础上引入4条辅助支腿，并且使轮轨同时承担载荷，达到降低单个支腿工作载荷目的，满足高铁救援起重工作的严苛条件。

关于4支腿支撑结构形式的支腿反力计算已有大量研究人员对此做出研究。李以申[3]分析了传统4支腿模型支腿反力两种不同计算方法的谬误。荣国瑞[4]应用力学方法在考虑支腿刚度的条件下求解得到了支腿反力，并以反向补偿的方式解决了支腿起翘后的反力计算问题。房晓文[5]在同时考虑车架大梁扭转及支腿弯曲变形的基础上，推导出了起重机支腿反力的计算公式。但是随着起重机工作环境的变化，例如高架桥、冻原等特殊的作业环境下，使用4支腿起重机可能会引起支腿载荷超限、载荷分布不均等问题的出现，这时候就需要增加支撑的数量。王健[6]提出了一种五支腿起重机支腿反力计算方法。刘振国[7]使用力学中的相关计算方法得到了一种八支腿起重机支腿反力的计算方法。

针对一种高速铁路救援起重机多支撑机构，本文使用结构力学中的超静定结构力法原理[8]来进行解析计算，并对实际算例进行刚柔耦合仿真加以验证。

1 高铁救援起重机多支撑结构及其力学模型

整个起重机承载结构由车架大梁、4个内侧伸缩支腿，4个外侧摆动支腿以及轮轨支撑组成，整个下车结构为对称布置如图1所示。

图1 高铁救援起重机下车结构模型

由于轮轨和车体是通过转向架连接，本研究在把车体简化成受力模型时将轮轨受力集中到前后两个转向架上，即在原8支腿支撑结构中增加两个支点，支点位置在中央主支撑梁上，类似于其他承载支腿，两个支点对负载和力矩进行承载。

受力分别为F9、F10如图2所示。

图2 高铁起重机力学模型

该结构为空间七次超静定结构。

2 高次超静定结构的力法计算方法

力法是最为基本的求解超静定问题的方法，力法的基本思想是将超静定结构通过去除多余约束来拆解成静定结构。

一次超静定结构如图3所示。

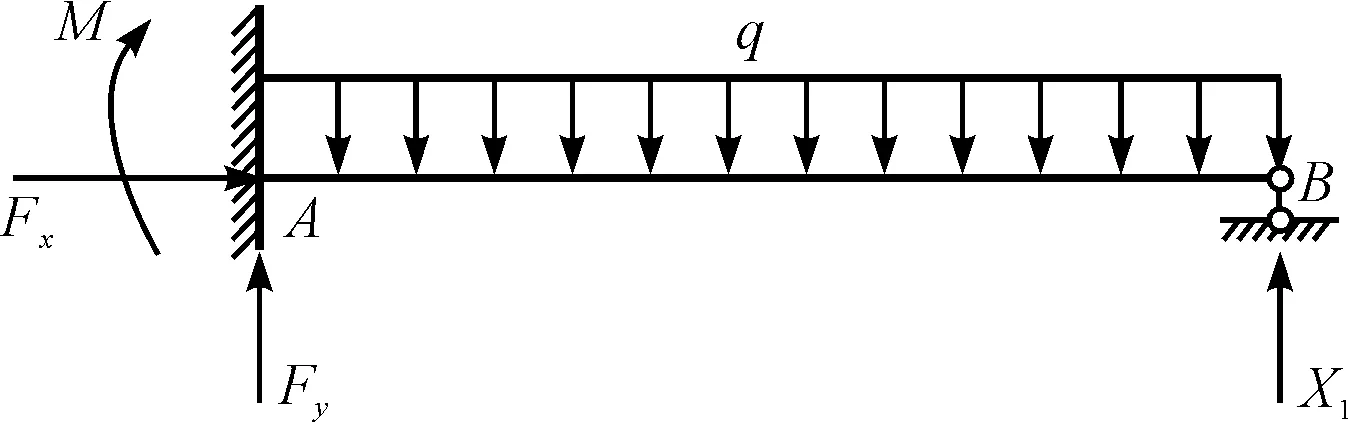
图3 一次超静定结构

静定结构如图4所示。

图4 静定结构

本研究通过在静定结构条件下建立的变形协调方程来过渡到超静定结构。

由受力图可知：静定结构中简支梁受3个未知力(或力矩)Fx、Fy、M，可用平面任意力系的3个平衡方程全部求出；一次超静定结构中简支梁在B点受到额外的一个支座反力X1，此时梁总共受到4个约束力无法由3个平衡方程求出全部未知力(或力矩)。

在超静定结构中遇到的新问题就是求解超出平衡方程个数的未知力(或力矩)。一般可以通过构造变形协调方程来增补方程个数，从而使方程个数与未知力(或力矩)个数相同。

下面讨论n次超静定结构的基本方程建立方法。当结构为n次超静定结构时(n>2)，结构中的基本未知量为n个多余未知力X1、X2、…、Xn。力法的基本体系是从原结构中去掉n个多余约束，而代之以相应的n个多余未知力后所得到的静定结构，力法的基本方程是在n个多余约束处的n个变形条件，即基本体系中沿多余未知力方向的位移应与原结构中相应的位移相等。

在线性变形体系中，根据叠加原理，n个变形条件通常可写为：

(1)

式中：ΔiP—由载荷产生的沿Xi方向的位移；δij—由单位力Xj=1产生的沿Xi方向的位移，常称为柔度系数。

其中，当位移方向与相应的力的正方向相同时，位移符号规定为正。根据位移互等定理，系数δij和δji是相等的。

关于载荷作用下的位移ΔiP，结构力学中提供了相关的计算公式：

(2)

式中：MP，FP，TP—代表由实际加载载荷P引起的结构的弯矩、轴向力和扭矩；Mi，Fi，Ti—代表由虚设单位载荷Xi引起的结构的弯矩、轴向力和扭矩。

柔度系数δij即由单位力Xj=1产生的沿Xi方向的位移，可以由以下公式计算：

(3)

式中：Mj，Fj，Tj—代表由虚设单位载荷Xj引起的结构的弯矩、轴向力和扭矩；Mi，Fi，Ti—代表由虚设单位载荷Xi引起的结构的弯矩、轴向力和扭矩；

由此，将计算所得各项柔度系数和载荷作用下沿各分支方向产生的位移代回式(1)中，加上垂直方向力平衡方程和X轴、Y轴方向转矩平衡方程，即可求解得到各分支方向承受反力数值。

3 高铁救援起重机多支撑结构力学解算

该多支撑结构为7次超静定结构，取6、7、8支腿为基本支腿，列出相关的7次超静定力法方程：

(4)

至此，该多支撑结构力法方程系数已完全建立。本研究假设从图2建立的坐标系原点到转向架连接点处的距离为相关支点的计算用支腿长度，利用铁木辛柯梁理论计算出相关的截面等效刚度。

将7次超静定结构的力及力矩平衡方程加入到力法方程中，得到包含10个未知数和10个方程的线性方程组：

(5)

式中：ai—代表第i条支腿在坐标系中X轴方向坐标值；bi—代表第i条支腿在坐标系中Y轴方向坐标值；

取两种不同的工况，编写Matlab程序计算结果如下。

(1)起重载荷为160 t，车体质量为110 t，起重力矩为5×108N·m，使起重臂回转一周，所得曲线如图5所示。

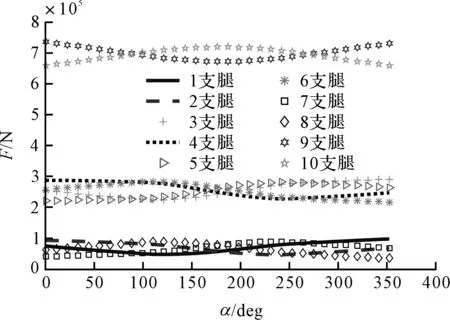
图5 计算所得160 t负载下各支点负载情况

从分析结果可以看到，在给定工况下，受力最大的支腿为前后两个转向架，承载了大部分载荷，负载最大时为7.5×105N；随着起重机上车起重臂的转动，各支腿受力情况发生变化，与转动方向同一Y轴半区的4条支腿受力增加，而另4条支腿受力减少，反之亦然。在工作过程中，内侧伸缩支腿受力最大值约为3×105N，外侧伸缩支腿受力最大值约为105N。

(2)起重载荷为200 t，车体质量为110 t，起重力矩为7×108N·m，使起重臂回转一周，所得曲线如图6所示。

图6 计算所得200 t负载下各支点负载情况

从分析结果可以看到，在给定200 t工况下，受力最大支腿依然为前后两个转向架，承载了绝大多数的负载，负载最大时为9×105N；随着起重机上车起重臂的转动，各支腿受力情况发生变化，与转动方向同一Y轴半区的4条支腿受力增加，而另4条支腿受力减少，反之亦然。在工作过程中，内侧伸缩支腿受力最大值约为3.5×105N，外侧展开支腿受力最大值约为1.2×105N。

4 刚柔耦合仿真结果对比

由于引入了转向架作为支撑点，建立了新的三维模型，并对模型重新划分网格[9]如图7所示。

图7 动力学仿真软件中的柔性体模型

(1)在仿真软件中设定工作条件为：

起重量160 t，起重力矩5×108N·m。

仿真曲线如图8所示。

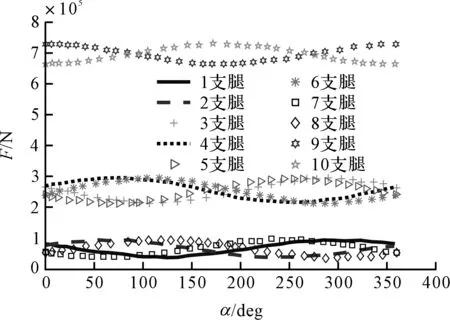
图8 160 t时起重臂转动一周支腿受力曲线

从仿真结果看出，受力最大的支腿为前后两个转向架，承载了绝大多数的负载，负载最大时为大约8×105N。内侧伸缩支腿最大负载为2.7×105N。

(2)在仿真软件中设定工作条件为：

起重量200 t，起重力矩7×108N·m。

仿真曲线如图9所示。

图9 200 t时起重臂转动一周支腿受力曲线

从仿真结果看出，受力最大支腿依然为前后两个转向架，承载了绝大多数的负载，负载最大时为大约9.5×105N。内侧伸缩支腿承载支腿最大负载为3×105N。

由于建立的是刚柔耦合仿真模型，仿真过程中设定的负载较大时，多支撑结构会出现一定的振动现象，但对支反力的影响不大。软件仿真的整个工作过程中，受力最大的支点为前后两个转向架，负载最大时为大约7.5×105N。展开支腿的受力的最大值约为3×105N。

与Matlab程序计算的解析解相比，数值和趋势基本一致，验证了解析模型的正确性。

5 结束语

本文利用空间高次超静定原理求解了一种高速铁路救援起重机多支撑机构支撑反力，并对机构进行了刚柔耦合仿真，仿真结果与解析解结果趋势基本一致，验证了解析模型的正确性，该方法可以推广到类似多支撑机构的支撑反力计算中。

在引入轮轨受力之后，相对于八支腿支撑受力，各支腿的受力大为减小，从而降低了高架桥面受到的破坏风险，提升了安全性；同时从计算结果的对比中可以看出，在较大工作载荷下，支腿的起翘现象得到了改善，进一步提升了起重机工作的稳定性与安全性。

在建立支腿系统刚柔耦合模型时，忽略了一些因素的影响，有必要通过实验进行数据的采集，进行更精确的建模。

此外，为了精确分析多支撑结构的动态性能，需要对其进行动力学建模，从而为高速铁路救援起重机下车部分支撑机构的设计提供可靠的依据。

参考文献(References):

[1] 孟 钢.沪杭高铁横潦泾大桥快速施工管理实践研究[D].成都：西南交通大学土木工程学院,2015.

[2] EBRAHIMI M, GHAYOUR M, MADANI S M, et al. Swing angle estimation for anti-sway overhead crane control using load cell[J].InternationalJournalofControl,AutomationandSystems.2011,9(2):300-309.

[3] 李以申.试评轮胎式起重机支腿反力的几种计算方法[J].建筑机械,1989(2):48-52.

[4] 荣国瑞.汽车起重机支腿压力的新算法[J].重庆建筑大学学报,1997,19(3):49-54.

[5] 房晓文.汽车起重机支腿反力简化计算方法与实验验证[J].起重运输机械,2012(6):89-92.

[6] 王 健,周 静,崔晓琳，等.五支腿起重机支腿力计算方法研究[J].农业装备与车辆工程,2009(11):19-21.

[7] 刘振国,滕儒民,吴海帆,等.一种八支腿起重机支腿反力研究[J].机械设计与制造,2015(5):12-14.

[8] 龙驭球,包世华,匡文起,等.结构力学教程(Ⅰ)[M].北京：高等教育出版社,2000.

[9] 徐国宝，马金凤，王延军，等.基于ADAMS的跌落式装箱机动力学仿真研究[J].包装与食品机械，2016(1)：44-47.