球头接触副对柱式负荷传感器方位误差的影响研究*

陈俊翔，梁 伟,，杨晓翔,3*，姚进辉

(1.福州大学 机械工程及自动化学院，福建 福州 350116；2.福建省计量科学研究院，福建 福州350003；3.泉州师范学院，福建 泉州 362000)

0 引 言

应变式负荷传感器由球头接触副、传感器主体、底座组成，而传感器主体又包含了弹性体、应变片及惠斯通电桥。柱式负荷传感器具有：结构简单紧凑、便于安装；弹性元件刚度大、固有频率高、动态响应快；良好的抗冲击和抗侧载能力等优点[1]。

柱式负荷传感器上的负载必须尽可能作用在弹性体轴心方向上。附加弯矩和侧向力等寄生分量都是测量结果的干扰因素，当其超过允许极限时，将直接损坏传感器。对于非固定安装使用的柱式负荷传感器，使用时安装位置存在随意性，寄生分量将造成传感器在不同方位上的示值发生改变，从而产生方位误差，影响被测对象的测量结果[2]。因此，控制好传感器寄生分量对于改善传感器方位误差、提高负荷测量结果的准确度具有重要意义。

方位误差作为负荷传感器等级评判的一个重要指标，目前对此展开的研究十分广泛。Bray A等人[3]提出传感器结构的不对称性和力标准机材料的不均匀性是引起方位误差的根本原因。Peters M等人[4-5]通过大量的比对试验发现，附加弯矩及力的非轴向分量是产生方位误差的直接原因。Nile S[6-7]发现补偿平台的弯曲刚度不足会导致方位误差的产生。因此，研究人员又提出了许多减小方位误差的措施。Andrae J等人[8]提出改善传感器结构的对称性有利于减小方位误差；Kang D I等人[9]提出通过弯矩补偿可有效抑制由平行度引起的方位误差。

球头接触副作为传感器的重要组成部分，主要起到将被测力值传导至弹性体的作用。依赖其球面结构，可以通过球面滚动有效改善因被测载荷作用方向倾斜对测量结果造成的影响，对传感器的整体性能表现有重要的作用。

本文以300 kN柱式负荷传感器为研究对象，在其常用球面尺寸范围内选定球头接触副的接触类型、接触副球面尺寸，并对被测传感器进行理论计算、有限元仿真分析，结合负荷特性试验探究球头接触副对柱式负荷传感器方位误差的影响，总结出球头接触副球面尺寸变化对传感器方位误差的影响规律。

1 传感器理论计算

1.1 被测传感器工作原理

本文选用某厂商LC-3 300kN 0.3级柱式负荷传感器为研究对象，其应变片贴片方式如图1(a)所示，其中应变片1、4测量纵向应变，应变片2、3测量横向应变；桥式电路如图1(b)所示，R1、R2、R3、R4表示应变片阻值，电桥输出电压为[10]：

(1)

式中：Ui，Uo—电桥输入、输出电压，V；K—应变片灵敏系数；ε1，ε2，ε3，ε4—应变片应变。

在传感器加工过程中，应变片手工粘贴位置必然存在偏差，难以保证应变片1、4或应变片2、3处在弹性体横截面的同一直径上，应变片粘贴方位偏移如图1(c)所示，定义应变片4偏移角度为α，应变片3偏移角度为β。

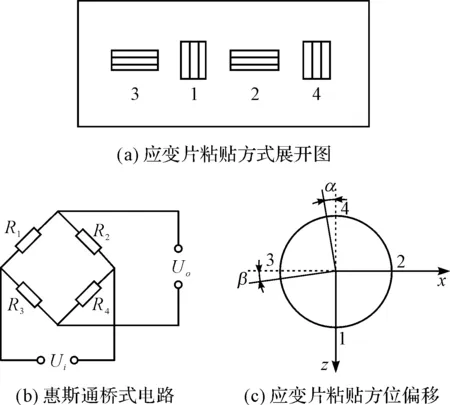
图1 被测传感器主要结构示意图

倾载作用下传感器受力示意图如图2所示。

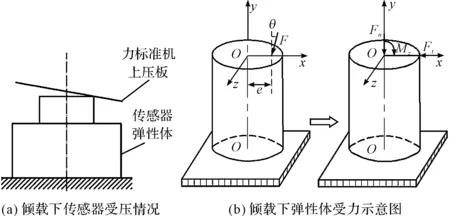
图2 倾载作用下传感器受力示意图

如图2(a)所示，由于传感器自身结构缺陷、测量基准面倾斜亦或是被测载荷存在一定的倾角等原因，将导致被测载荷与传感器轴线之间存在不应有的夹角，使被测载荷集中作用在弹性体上某一点。此时弹性体受力情况如图2(b)所示，将弹性体近似为实心圆柱体，被测倾载F简化为与弹性体轴线重合的竖直载荷Fn、横向载荷Ft及附加弯矩Mz。

本文主要研究球头接触副对传感器所受附加弯矩Mz的影响，其对传感器所受横向载荷Ft无改善作用，且当传感器受小角度倾载作用时，横向载荷Ft数值较小，故仅考虑在附加弯矩Mz及竖直载荷Fn的作用下，传感器各应变片产生的应变：

(2)

(3)

(4)

(5)

Fn=Fcosθ

(6)

S=πr2

(7)

Mz=Fecosθ

(8)

(9)

式中：F—被测倾载，kN；Fn—与弹性体轴线重合的竖直载荷，kN；S—弹性体横截面积，mm2；Mz—传感器所受附加弯矩，N·m；x1，x2，x3，x4—应变片粘贴处x轴坐标，mm；Iz—弹性体横截面对z轴的惯性矩，mm4；E—弹性体材料杨氏模量，GPa；μ—弹性体材料泊松比；r—弹性体横截面半径，mm；θ—被测载荷与传感器轴线夹角，°；e—被测载荷作用点偏心距，mm。

1.2 传感器方位误差计算

本研究参照《GB 13634-2008-T单轴试验机检验用标准测力仪的校准》[11]，对传感器方位误差进行计算：

(10)

(11)

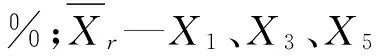
将各方位下的x1、x2、x3、x4代入式(2～5)，并联立式(1～11)可得：

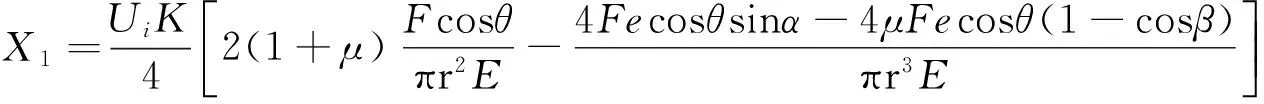
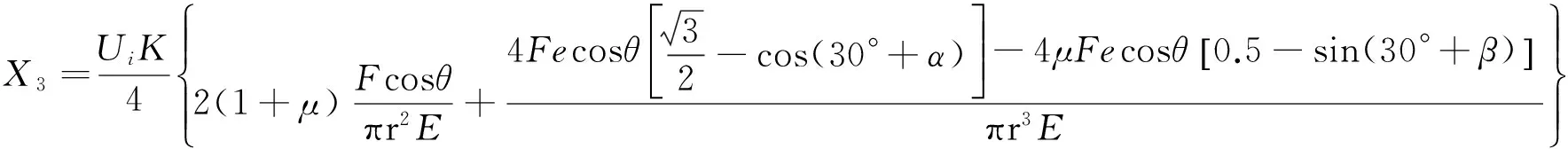
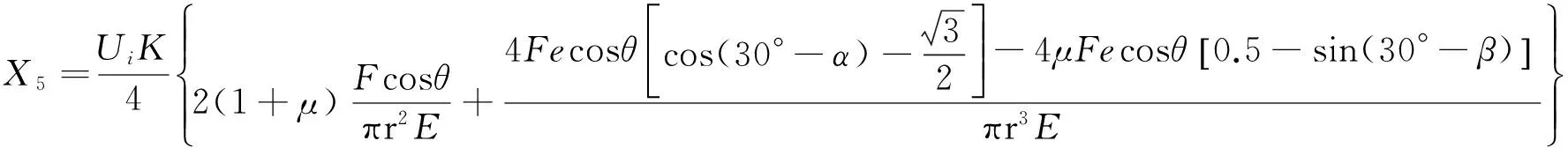
(12)

由式(12)可知：传感器方位误差b受被测载荷作用点偏心距e、弹性体材料泊松比μ、弹性体横截面半径r、应变片偏移角度α、β等因素的影响。当传感器出厂后，μ、r、α、β成为定值。此时，结合式(8，12)可知：在同一被测倾载F作用下，传感器方位误差随着被测载荷作用点偏心距e的减小而减小，即随着传感器所受附加弯矩Mz的减小而减小。

1.3 球头接触副工作原理

球头接触副主要分为球面-球面接触副及球面-平面接触副两种类型。球面-球面接触副多见于轮辐式称重传感器；柱式负荷传感器常将弹性体顶端加工为球状结构，配合平面压头作为球面-平面接触副进行使用。本文选用柱式负荷传感器为研究对象，主要讨论球面-平面接触副对其方位误差的影响。

在被测载荷存在倾角的情况下，球头接触副能依赖其球面结构，通过球面滚动有效调节被测载荷作用区域，使其尽可能贴近弹性体轴线，减小传感器所受附加弯矩。装配球面-平面球头接触副的情况如图3所示。

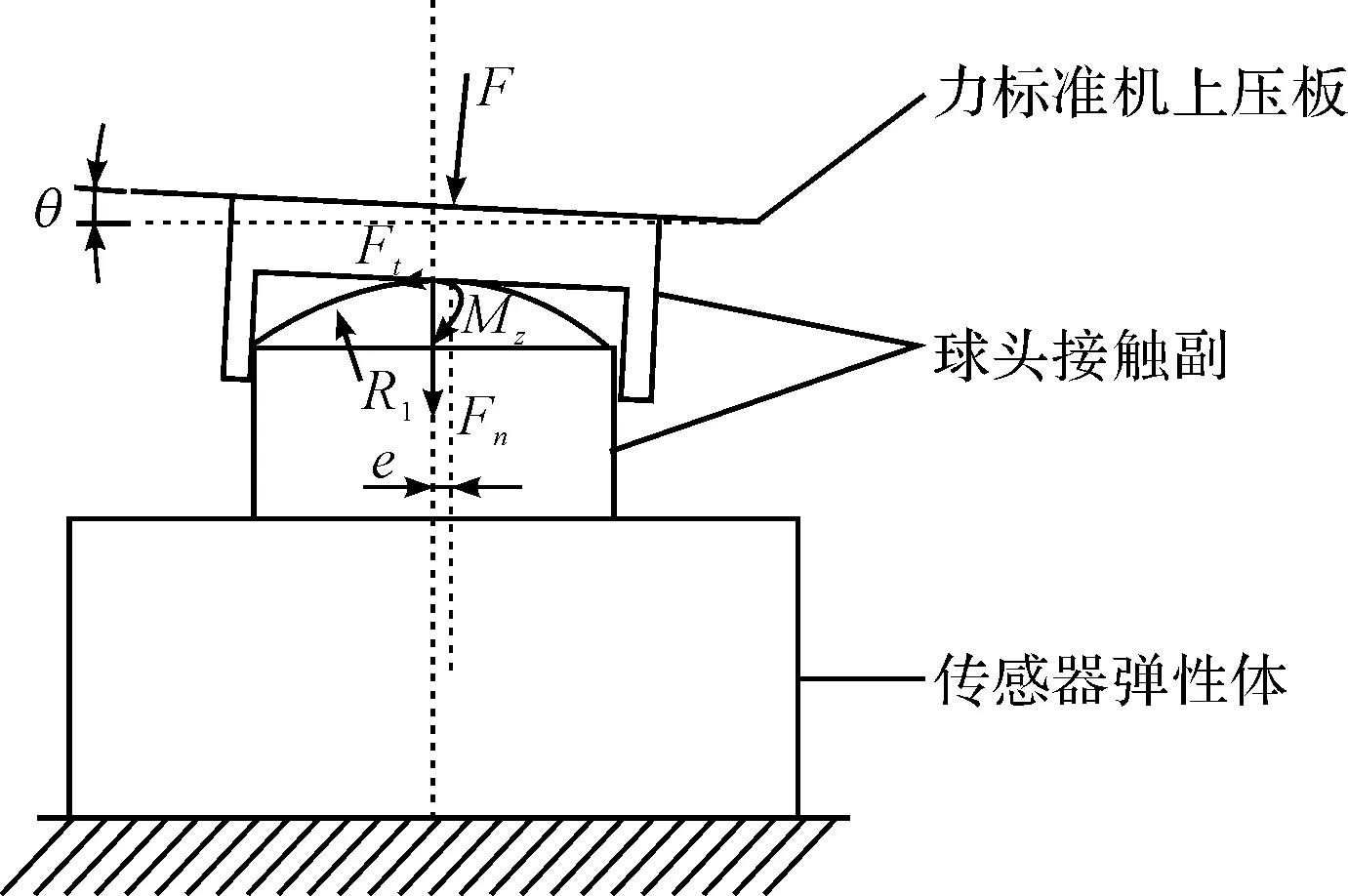
图3 球面-平面球头接触副作用效果图

施加倾载F时，力标准机上压板将与接触副压头上一点先接触，由于接触副球头与压头间的相对滚动，使得被测载荷作用点贴近弹性体轴线，此时倾载F简化为横向载荷Ft、与弹性体轴线重合的竖直载荷Fn及附加弯矩Mz作用于传感器上：

e=R1sinθ

(13)

式中：R1—接触副球头球径，mm。

联立公式(8，12，13)可得：

(14)

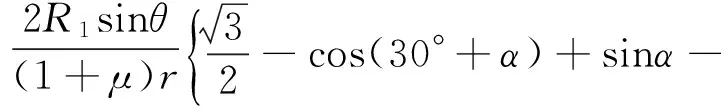
μ[1.5-sin(30°+β)-cosβ]}×100%

(15)

由此可以看出：在同一被测倾载F作用下，即θ不变的情况下，传感器所受附加弯矩Mz随着球头球径R1的减小而减小，方位误差b也将随之减小。装配同一球头接触副时，即R1不变的情况下，传感器所受附加弯矩Mz随着被测载荷倾角θ的减小而减小,方位误差b也将随之减小。

1.4 球头接触副尺寸及材料参数确定

球头接触副的材料多选用40CrNiMo、0Cr17Ni4Cu4Nb等优质钢材，考虑到其滚动体的外形特征及大负载工作条件，本研究决定选取优质轴承钢GCr15SiMn作为球头接触副加工材料。

GCr15SiMn适用于加工球径大于50 mm的滚动体。其部分材料属性如表1所示[12]。

表1 GCr15SiMn材料属性

参考市场主流300 kN柱式负荷传感器的球头接触副球面尺寸可知：其球头球径R1多分布于100 mm～400 mm区间内，为了尽可能完整地覆盖该尺寸区间，决定对R1=150 mm、200 mm、250 mm、300 mm、350 mm的5组球面-平面球头接触副开展研究。

2 有限元仿真分析

2.1 有限元模型的建立

为了研究球头接触副球面尺寸变化对传感器所受附加弯矩的影响规律，本研究在ABAQUS中建立传感器有限元模型进行仿真分析。

被测传感器弹性体材料为40CrNiMo，其部分材料属性如表2所示。

表2 40CrNiMo材料属性

建立的有限元网格模型如图4所示。

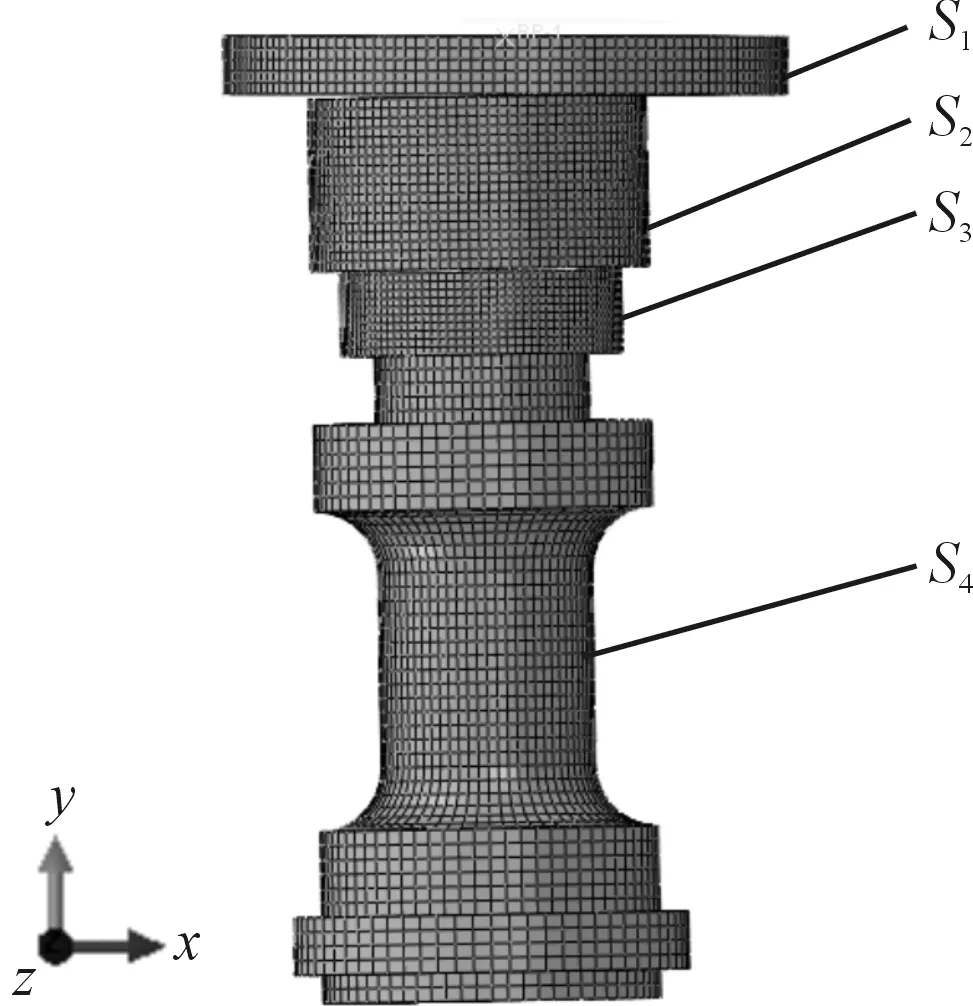
图4 传感器有限元网格模型

图4中，力标准机上压板设置为刚体，由S1代替；接触副压头与接触副球头由S2、S3代替，传感器弹性体由S4代替。S2、S3选用主从接触算法，将表面加工硬度较大的S2内表面设为接触主面，表面加工硬度较小的S3外表面设为接触从面。根据主从面网格划分规律，对从面的网格划分较之主面更为细密[13]。

模型各部件主要几何参数如表3所示。

表3 模型各部件主要几何参数

本研究采用C3D8R八节点三维实体单元进行模型网格划分，共划分87 840个单元，96 167个结点。为了模拟被测载荷相对弹性体轴线存在倾角θ的情况，在S2、S3、S4装配后将其绕z轴旋转θ，S1下表面相对xz面平行且与S2上表面边线上一点接触。

根据柱式负荷传感器在力标准机上的实际加载情况进行模型边界条件的设置[14]：S4下表面定义全约束(U1=U2=U3=0)；S1上表面圆心处的参考点RP-1约束除Y方向以外的2个自由度(U1=U3=0)；S1上表面施加合力为300 kN且垂直加载面的均布载荷。在倾角θ设为0.5°及1°的情况下分别装配5组球头接触副进行仿真分析。

2.2 有限元解与理论解的比较及分析

为了便于提取仿真分析结果，笔者于S4上定义过轴线且法线垂直于Z轴的截面，输出并比较不同倾载下、装配不同尺寸球头接触副时该截面所受弯矩，以此衡量传感器方位误差的大小。

装配不同球面尺寸的球头接触副时，在300 kN 0.5°及300 kN 1°倾斜载荷作用下传感器所受附加弯矩的变化曲线如图5所示。图中显示，有限元解数值变化规律与理论解数值变化规律相符：在同一倾载F作用下，传感器所受附加弯矩Mz的大小随着球头球径R1的减小而减小，因此传感器方位误差b也随之减小；装配同一球头接触副时，传感器所受附加弯矩Mz的大小随着被测载荷倾角θ的减小而减小,因此传感器方位误差b也随之减小。

理论解与有限元解之间存在误差的原因在于：理论求解时，球头接触副视为理想运动状态，发生无变形相对滚动，接触副球面尺寸不变化；有限元仿真时，球头接触副在相对滚动的过程中受压变形，接触副球头球径R1动态变化并增大，导致被测载荷作用点偏心距e增大，则传感器所受附加弯矩Mz增大，因此有限元解大于理论解，但更接近于真实情况。

球头球径R1对传感器所受附加弯矩Mz的影响规律如图5所示。

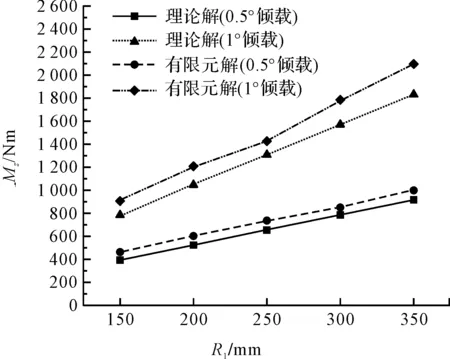
图5 球头球径R1对传感器所受附加弯矩Mz的影响规律

3 实验验证

3.1 传感器方位误差测量要求

为检验球头接触副减小传感器方位误差的作用，并验证理论解及有限元数值解规律的准确性。现笔者根据《GB 13634-2008-T 单轴试验机检验用标准测力仪的校准》[11]，采用300 kN叠加式力标准机对被测传感器进行负荷特性测量。

参照该标准，本研究对传感器预加3次额定试验力，在额定试验力保持30 s。开始测试时，均匀选择10个检测点，按试验力递增顺序逐点进行检测。在每级试验力加载完毕后，保持30 s，记录读数值，直到额定试验力，然后卸除试验力，在该角度方位重复测量一次。随后，将传感器绕其主轴线依次转到120°、240°方位，在新的角度方位上预加额定试验力一次并保持30 s，按试验力递增再递减检测一遍。利用公式(10～11)求得传感器方位误差。

3.2 未装配球头接触时方位误差测量值

本研究在未装配球头接触副的情况下，分别施加倾角θ为0°、0.5°、1°的300 kN实验力级对传感器方位误差进行测量。为了实现施加倾载的测试条件，本研究通过销轴在实验基准台上装配倾角为θ的斜台，再将被测传感器对中装配于斜台之上，模拟被测载荷倾斜的情况。

被测传感器方位误差b如表4所示。

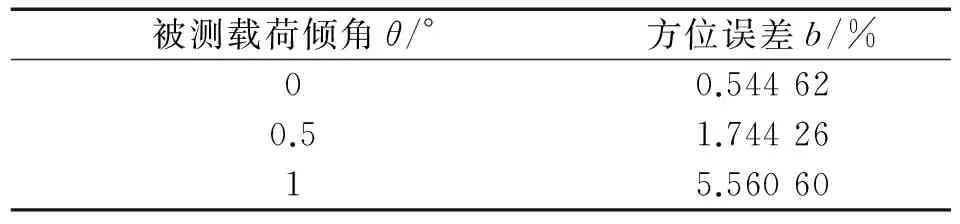
表4 被测传感器方位误差b(未装配球头接触副)

3.3 装配球头接触副时方位误差测量值

本研究在被测传感器上装配上述5组球面-平面球头接触副重复传感器方位误差的测量。实验同样分3次开展，分别施加倾角θ为0°、0.5°、1°的300 kN实验力级，测量结果如表5所示。

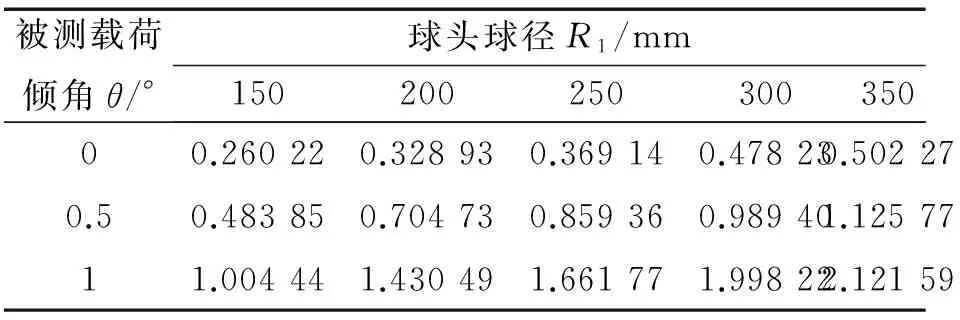
表5 被测传感器方位误差b/%(装配球头接触副)

3.4 测量结果的比较与分析

比较表(4，5)可知，传感器在装配球头接触副的情况下，其方位误差测量值小于未装配球头接触副时的测量值。通过计算可得，当θ=0°时，传感器方位误差减小了7.776%～52.220%；当θ=0.5°时，传感器方位误差减小了35.459%～72.260%；当θ=1°时，传感器方位误差减小了61.846%～81.936%。

不同倾载作用下，传感器装配5组球面-平面球头接触副时方位误差测量值如图6所示。

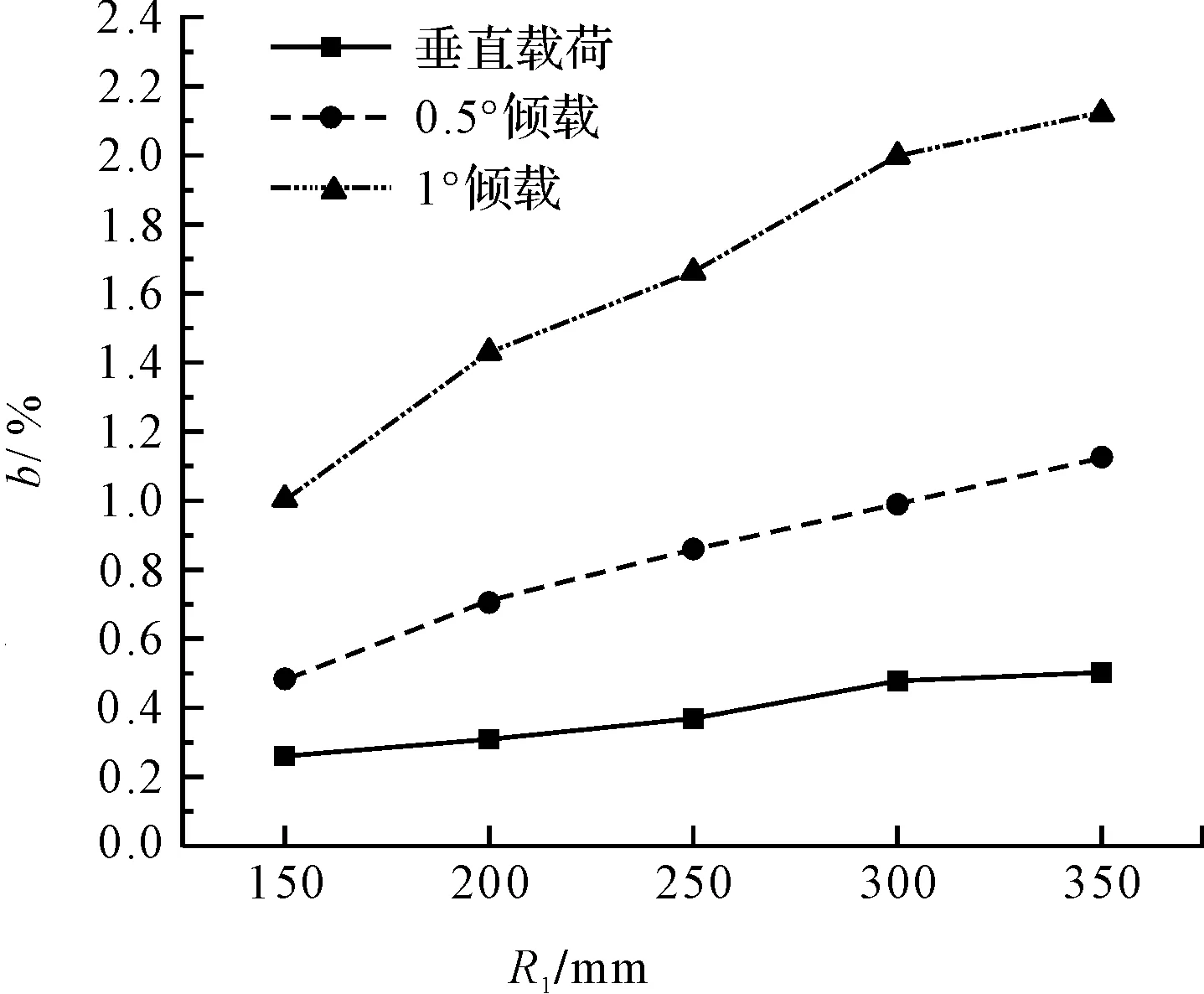
图6 方位误差测量结果

由此可知，在同一被测倾载F作用下，随着接触副球头球径R1的减小，传感器方位误差b也随之减小。装配同尺寸球头接触副即R1相等时，随着被测载荷倾角θ的减小，传感器方位误差b也随之减小。

不同倾载作用下，传感器装配5组球面-平面球头接触副时方位误差测量值的减小比例(相较于未装配球头接触副时的测量值)如图7所示。

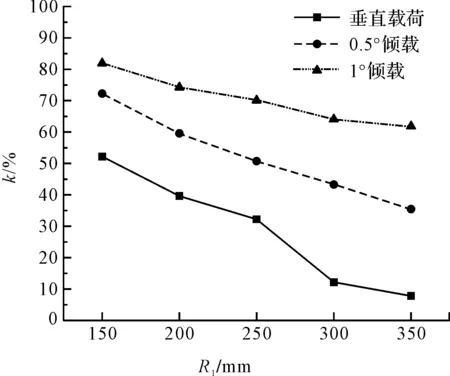
图7 传感器方位误差减小比例

由此可知，在同一被测倾载F作用下，随着接触副球头球径R1的减小，传感器方位误差减小比例k增大，球头接触副减小传感器方位误差b的效果愈发显著；装配同尺寸球头接触副即R1相等时，随着被测载荷倾角θ的增大，传感器方位误差减小比例k增大，球头接触副减小传感器方位误差b的效果愈发显著。

通过实验测量结果可知，球面-平面球头接触副能显著减小柱式负荷传感器的方位误差。在同一被测倾载F作用下，当球头球径R1越小时，传感器方位误差b越小。装配同尺寸球头接触副即R1相等时，随着被测载荷倾角θ的减小，传感器方位误差b也随之减小。球头球径R1对传感器方位误差b的影响规律验证了理论解及有限元仿真结果。

4 结束语

本研究采用理论公式推导、有限元仿真分析及传感器负荷特性试验等方法，得到了球面-平面球头接触副对柱式负荷传感器方位误差的影响规律：

(1)当被测载荷相对传感器轴线存在倾角时，得益于球头接触副之间的球面滚动调节作用，使得载荷作用区域能更好地贴近于传感器轴线，有效抑制了附加弯矩的产生。相较于未装配球头接触副的情况，球面-平面球头接触副能有效减小柱式负荷传感器的方位误差，保证传感器具有良好的负荷特性；

(2)对于球面-平面球头接触副，在同一被测倾载F作用下，随着球头球径R1的减小，其对传感器所受附加弯矩Mz的抑制效果愈发明显，对传感器方位误差b的改善效果愈发显著；

(3)装配同尺寸球头接触副即R1相等时，随着被测载荷倾角θ的减小，传感器所受附加弯矩Mz及其方位误差b也随之减小。

此外，为了进一步分析球面-平面球头接触副对传感器方位误差等负荷特性的影响，接下来本文将对接触副球面硬度等因素开展进一步的实验和分析。

参考文献(References):

[1] 林鸿志,吴建伟,杨 莉,等.柱式传感器倾斜误差问题初探[J].衡器,2016，45(1):36-38.

[2] 姚进辉.组合式负荷传感器方位误差的减小[J].中国计量,2013(3):74-76.

[3] BRAY A, BARBATO G, FRANCESCHINI F, et al. Rotational and end effects: a model for uncertainty evaluation in force measurements by means of dynamometers[J].Measurement,1996,17(4):279-286.

[4] PETERS M. Limits to the uncertainty achievable in force transfer[J].Measurement,1984,2(4):197-202.

[5] FERRERO C. The measurement of parasitic components in national force standard machines[J].Measurement,1990,8(2):66-76.

[6] NIEHE S. A new force measuring facility for the range of 10 mN to 10 N[C]. Proc of the XVII IMEKO World Congress, Dubrovnik: [s.n.],2003.

[7] NIEHE S. Force measuring facility from the range of 1 mN to 10 N[J].MetrologySocietyofIndia,2005,20(3):239-248.

[8] ANDRAE J, HONS C, SAWLA A. High precision force transducer with new method for online compensation of parasitic effects[J].Measurement,2003,33(2):173-178.

[9] KANG D I, HONG C S. Rotation effects of force transducers on the output of a build-up system[J].Measurement,1994,14(2):147-156.

[10] 潘 炼.传感器原理及应用[M].北京:电子工业出版社,2012.

[11] GB 13634-2008-T.单轴试验机检验用标准测力仪的校准[S].北京:中国计量出版社,2008.

[12] 钟顺思,王昌生.轴承钢[M].北京:冶金工业出版社,2000.

[13] 陈开颜,宋笔锋,喻天翔,等.滚珠式操纵软轴中滚珠接触应力分析[J].机械科学与技术,2016(2):171-175.

[14] 韦铁平,杨晓翔,姚进辉,等.一种新的叠加系统旋转效应的评估指标[J].福州大学学报,2015,43(6):796-801.