电阻应变片敏感栅结构参数对应变传递的影响研究*

许艺青，杨晓翔,韦铁平，姚进辉

(1.福州大学 石油化工学院，福建 福州 350116；2.福州大学 机械工程及自动化学院，福建 福州 350116；3.泉州师范学院，福建 泉州 362000；4.福建工程学院 机械与汽车工程系，福建 福州350118；5.福建省计量科学研究院，福建 福州 350003)

0 引 言

因具有灵敏度高、测量精度高和稳定性强等特点，电阻应变式传感器被广泛应用于许多领域。电阻应变片作为敏感元件，是电阻应变式传感器的重要组成部分，其结构尺寸直接影响传感器的测量性能。

Fuyu等[1]设计出20 t的柱式传感器，并推导出了传感器非线性误差的计算公式。基于弹性力学理论求解了柱式负荷传感器长径比为0.6～1.0弹性体的应变值分布规律，韦铁平等[2]发现长径比对端部效应的灵敏度有重大影响。雷一鸣[3]讨论了应变片灵敏系数的变化对测量结果的影响，并给出了降低此影响的方法。Weymouth等[4]对各种金属电阻应变片进行介绍，并对应变片粘贴提出建议。Younis等[5]针对被测试件的高应变区域提出钻孔法使其应力集中，对该区域应变片选择提出了建议。Sarangi等[6]针对有边缘裂纹的试样，利用DS技术得出应变片的最佳贴片位置。段然等[7]通过拉伸试验研究影响应变片测试精度的因素，提出了提高应变片测量精度的措施。Tang K等[8]研制了一种PID温度控制系统的实验装置，完成了箔式应变片在77 K～293 K的温度范围内的敏感系数修正。张佳明等[9]建立了应变片标定系统,在20 ℃～800 ℃范围内对应变片的灵敏度、滞后和蠕变进行了标定，证明了高温应变片在800 ℃时具有良好的性能。Zike等[10]建立了电阻应变式传感器弹性体和应变片的三维模型，利用有限元法研究发现基底弹性模量对测量结果影响很大，并对其进行了修正。王彪等[11]等通过建立电阻应变计的二维应变传递模型，对其应变传递机理进行了分析，研究表明胶接层横向宽度越宽、厚度越薄、弹性模量越大，应变传递过渡区越小，平均应变传递率越大。王文瑞等[12]和胡玉梅[13]建立了简支梁、胶层和栅丝的三维模型，研究丝式应变片的应变分布，结果表明敏感栅越细、胶层厚度和弹性模量越小，测量精度越高，栅丝间距和长度具有最优值，并通过实验进行了验证。Larry Burrow[14]通过有限元分析了箔式应变片的基底、箔材的厚度和材料及应变片端环尺寸对应变片性能的影响。

综上所述，目前对于电阻应变式传感器的研究主要集中在传感器的静态特性、端部效应、应变片的粘贴工艺、应变传递原理、温度和结构参数对丝式电阻应变片性能的影响上，对箔式电阻应变片敏感栅几何参数对应变传递的影响研究则较少。

本研究通过建立三维简化模型，利用ANSYS有限元软件对不同敏感栅结构进行模拟，揭示其对应变片性能和电阻应变式传感器的应变传递误差影响。

1 电阻应变片工作原理及结构

电阻应变片是一种用途广泛的高精度力学传感元件，主要由敏感栅、基底、覆盖层及引出线所组成[15]。

敏感栅是应变片最重要的组成部分，常用材料有康铜、镍铬合金、铁铬铝合金、铂合金等。敏感栅结构主要由边栅、横栅、测量栅、过渡栅和焊接栅组成，如图1所示。

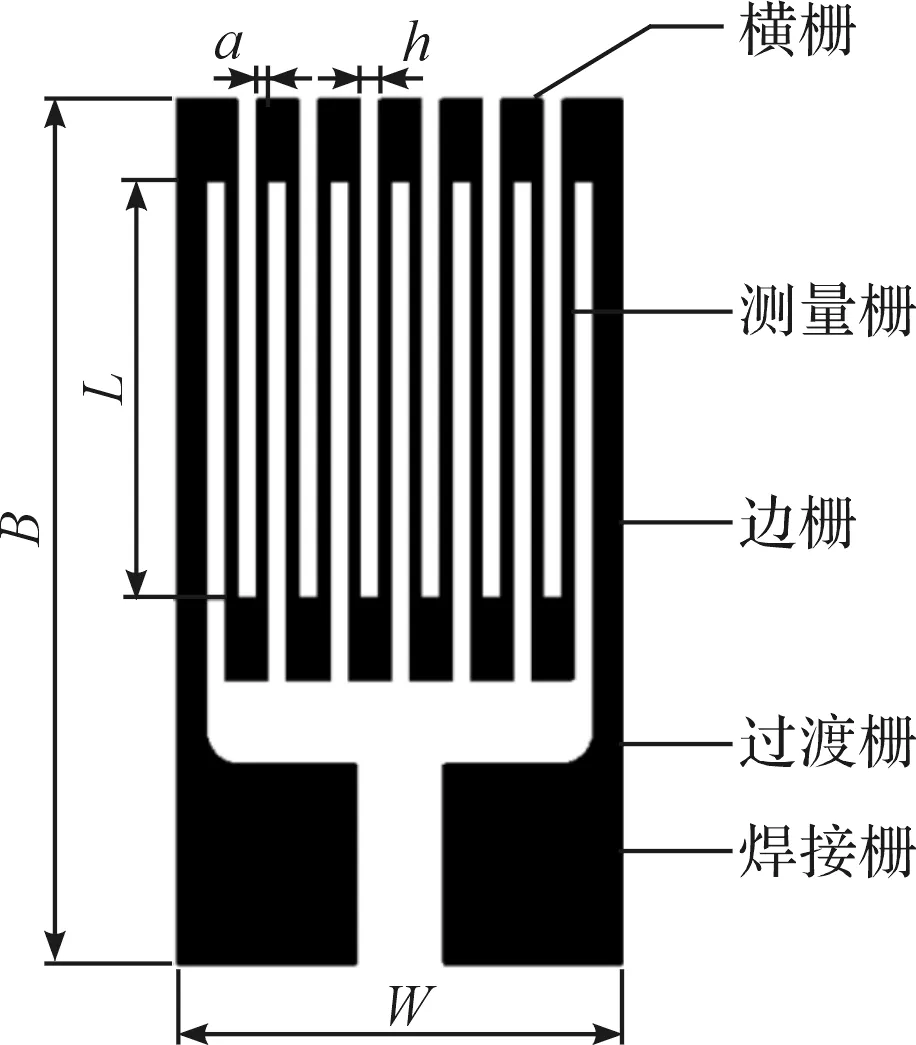
图1 敏感栅的典型结构B—敏感栅全长；L—敏感栅基长；W—栅宽；a—单栅丝宽度；h—栅丝间距

2 有限元模型建立及其验证

为研究传感器在测量状态下的应变分布，本研究建立了“等强度梁—基底—敏感栅—覆盖层”的有限元结构模型，各部分材料的力学性能[16]和几何参数如表1所示。

网格划分时对等强度梁与应变片基底交界处进行网格加密划分，有限元网格模型如图2所示。

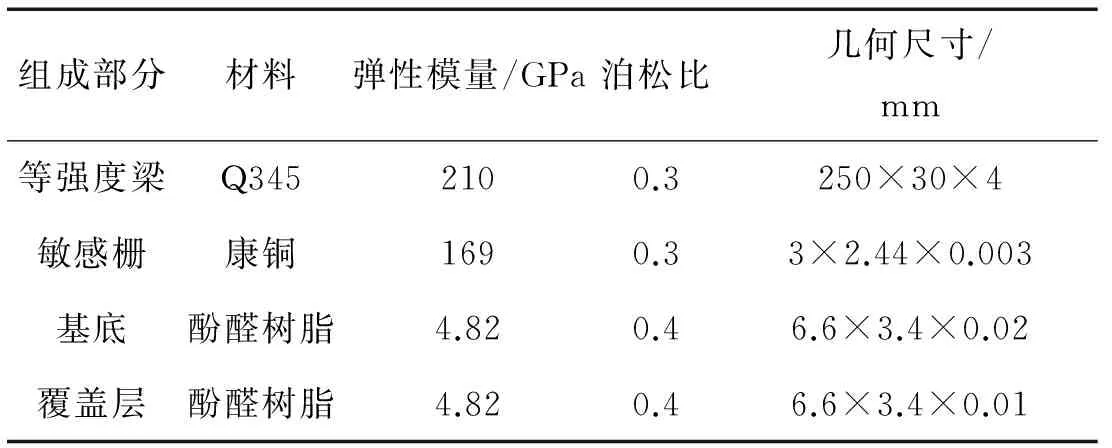
表1 各部分力学性能和几何尺寸

各部分均采用八节点六面体实体单元solid185，模拟时将三者设置绑定约束使其粘接起来，等强度梁的左端全约束，在右端施加载荷50 kN的力值。

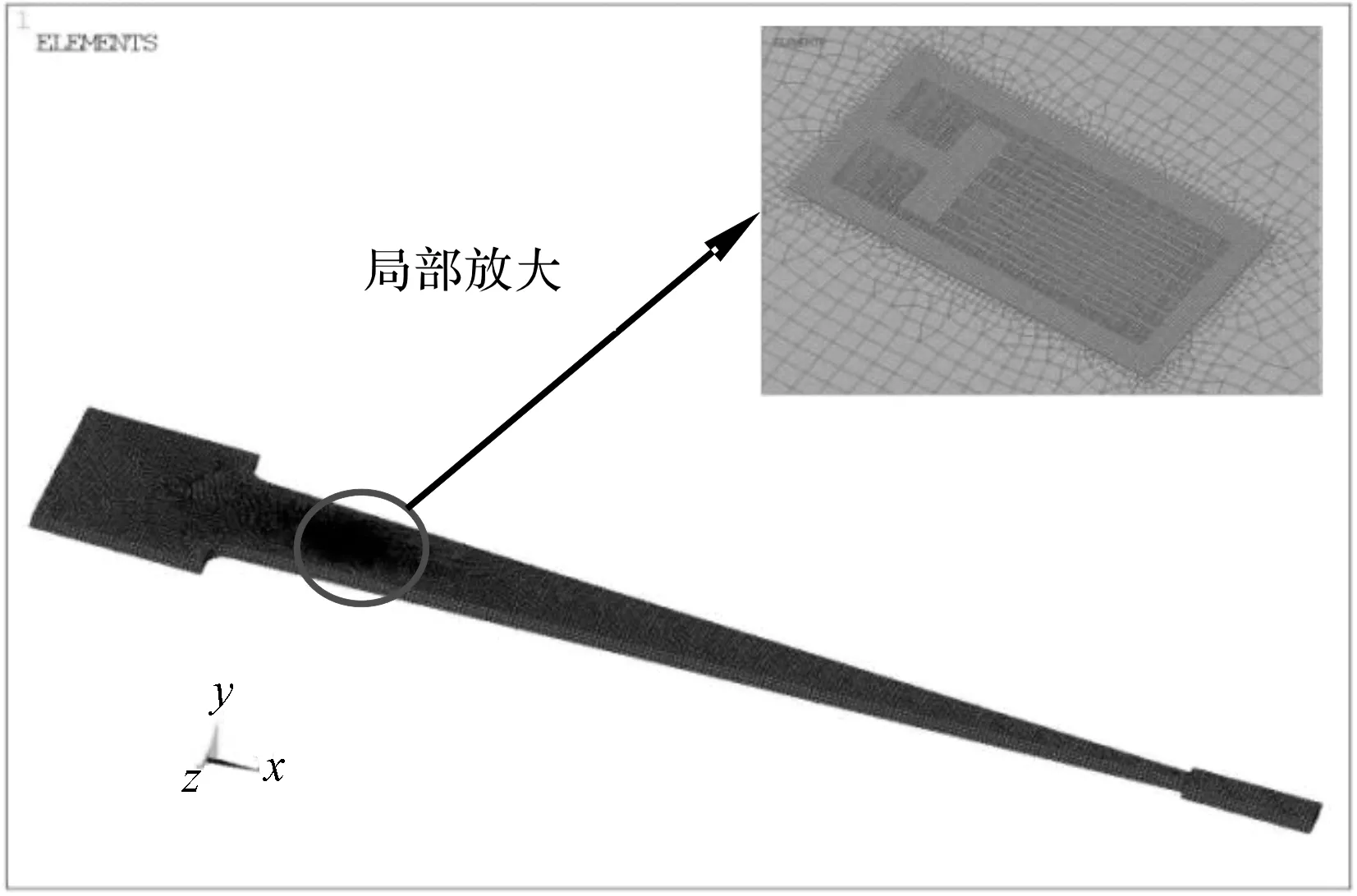
图2 有限元网格模型

根据材料力学知识可知，等强度梁贴片位置沿x轴方向的应变εs和自由端的挠度f为：

(1)

(2)

式中：Es—等强度梁弹性模量，MPa；F—等强度梁端部的外荷载，N；x—应变片中点与加载点的距离，mm；bs—等强度梁贴片位置的宽度，mm；ts—等强度梁的厚度，mm；Ls—等强度梁全长，mm。

等强度梁挠度云图和x方向应变云图分别如图3、图4所示。

图3 等强度梁挠度云图

图4 等强度梁x方向应变云图

从图中可以看出，等强度梁自由端的挠度为12.021 1 mm，与理论值偏差为1.39%，贴片位置的应变εs为6.90×10-4，与理论值偏差为2.54%，仿真结果与理论值计算基本一致。

应变片整体x方向应变云图如图5所示。

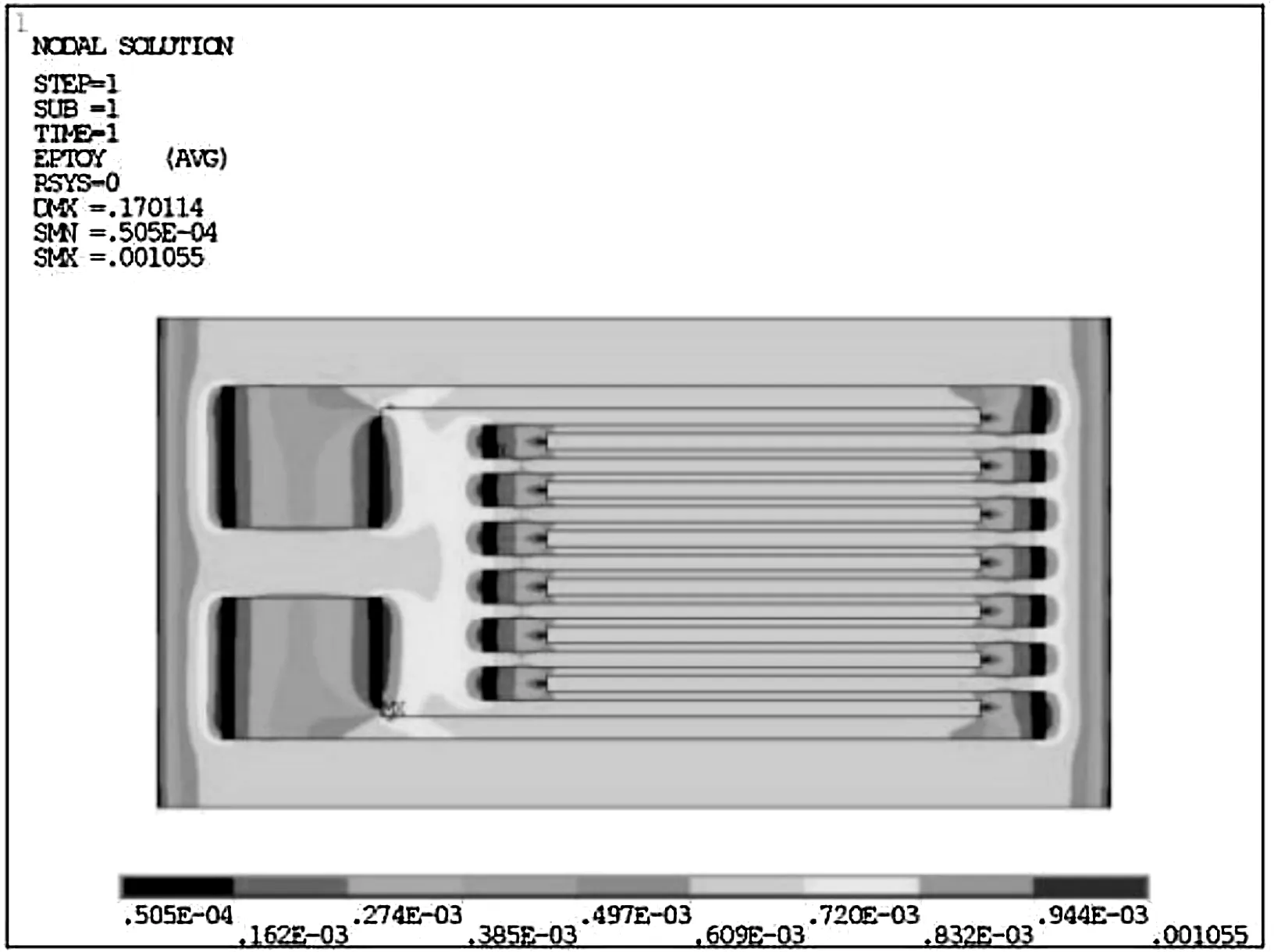
图5 应变片x方向应变云图

本研究将所有节点x方向的应变提取出来做平均值，绘制的应变分布图如图6所示。

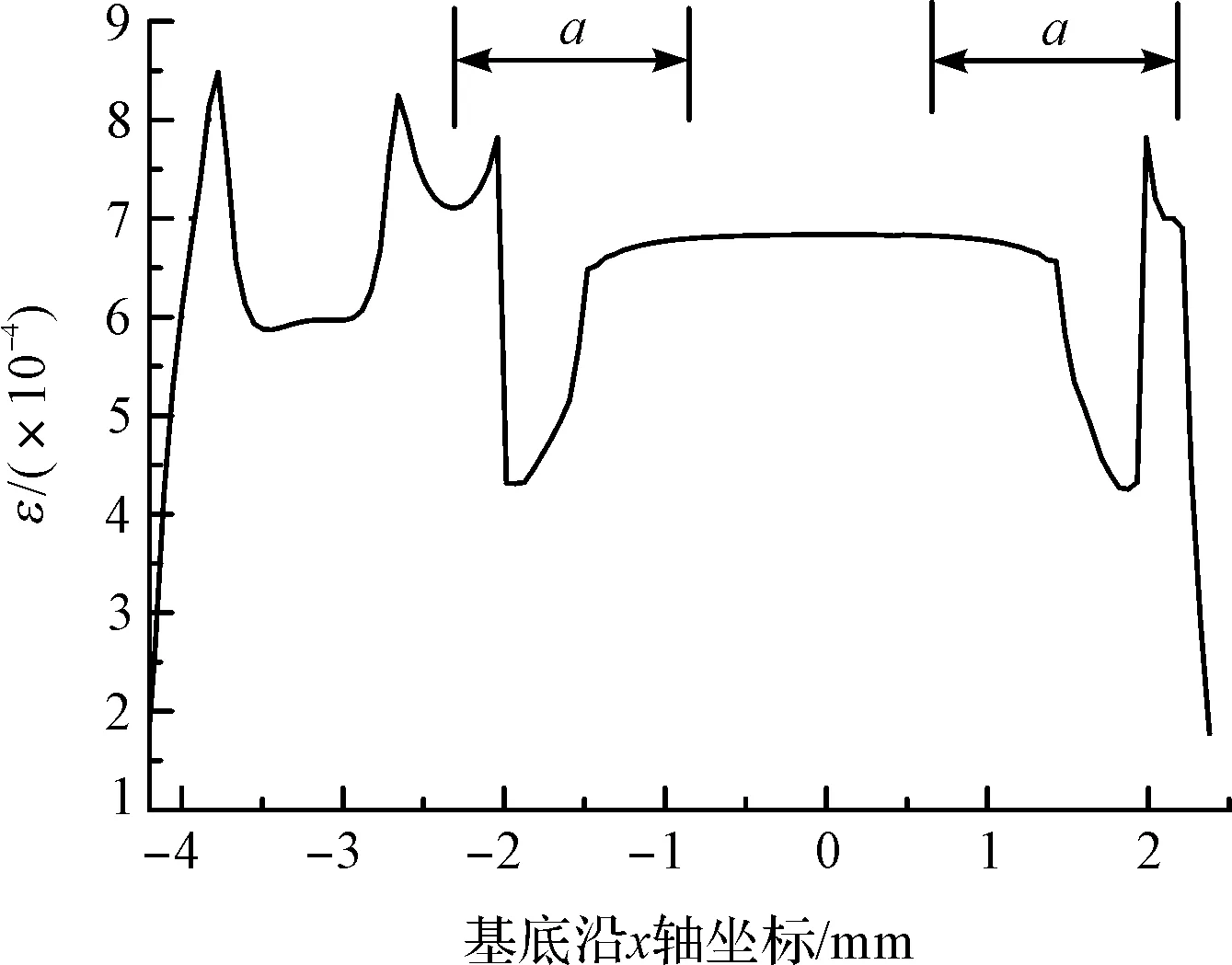
图6 应变片x方向应变分布

从图6可知，等强度梁向应变片传递应变时，基底与敏感栅之间存在应变过渡区，即图中a区域，该规律与Zike[10]研究结果一致。从图5中可以看出，应变片的两端不受力的作用，传感器受到外力作用产生的应变，是由各层之间的剪切应变传递给应变片敏感栅的，应力突变区域越小，越有利于应变传递。

取应变片测量栅中间20个节点x方向应变的平均值，作为应变片的测量值，则从传感器弹性体到敏感栅的应变传递率α为：

(3)

式中：εh—敏感栅x方向的应变。

3 应变片结构参数对应变传递的影响

影响传感器性能的主要因素之一是应变片敏感栅的结构参数，如其敏感栅材料、栅丝横截面积、栅丝间距、栅丝长度等。因此，本文基于有限单元法，重点分析这几个参数对应变片应变分布规律和应变传递误差的影响。敏感栅的焊接栅的截面积远大于栅丝截面积，由上述有限元结果可知焊接栅上的应变很小，故下述分析忽略焊接栅的影响。

3.1 敏感栅材料

应变片和等强度梁几何参数一定时，模拟康铜、铁铬铝合金、镍铬铝合金、铂铱合金4种合金下应变片敏感栅和基底的应变分布如图7、图8所示。

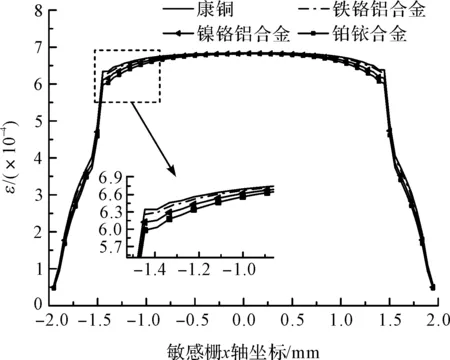
图7 不同敏感栅材料敏感栅x方向应变分布

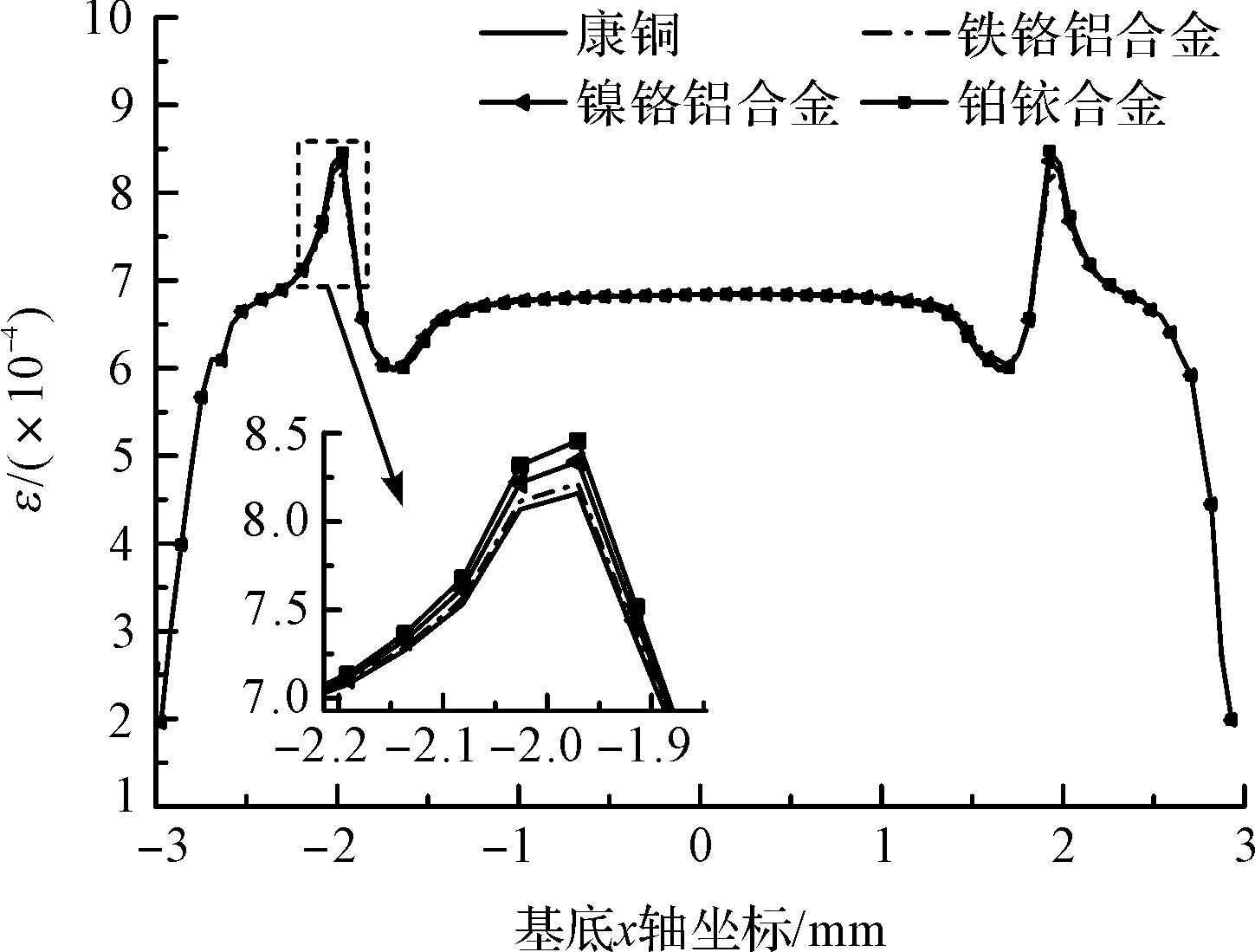
图8 不同敏感栅材料基底x方向应变分布

从图上可以看出，敏感栅材料弹性模量越小，敏感栅的应变分布越均匀，基底在应变突变区的x方向应变越小，即应变过渡区越小。

不同敏感栅材料应变传递误差如表2所示。

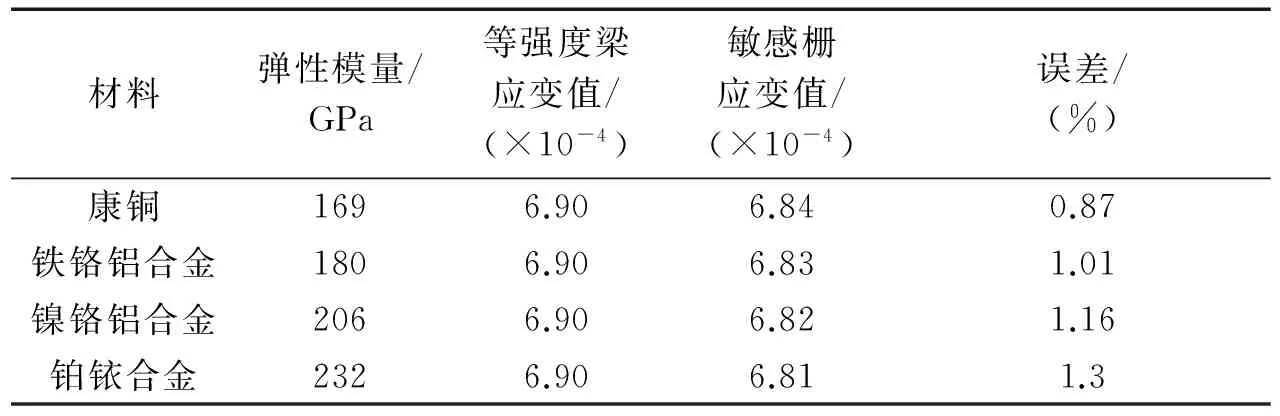
表2 不同敏感栅材料力学性能和应变传递误差

从表2中可以看出，康铜、铁铬铝合金、镍铬铝合金、铂铱合金的应变传递误差分别为0.87%、1.01%、1.16%、1.3%，弹性模量从169 GPa增加到232 GPa时，误差增加了0.43%，即随着敏感栅材料弹性模量的增大，应变传递误差也随之增大，但影响幅度不大。

3.2 敏感栅厚度

本研究保持其他参数不变，选取敏感栅厚度t为0.003 mm、0.005 mm、0.01 mm 3种情况进行模拟。不同敏感栅厚度时敏感栅和基底的应变分布如图9、图10所示。

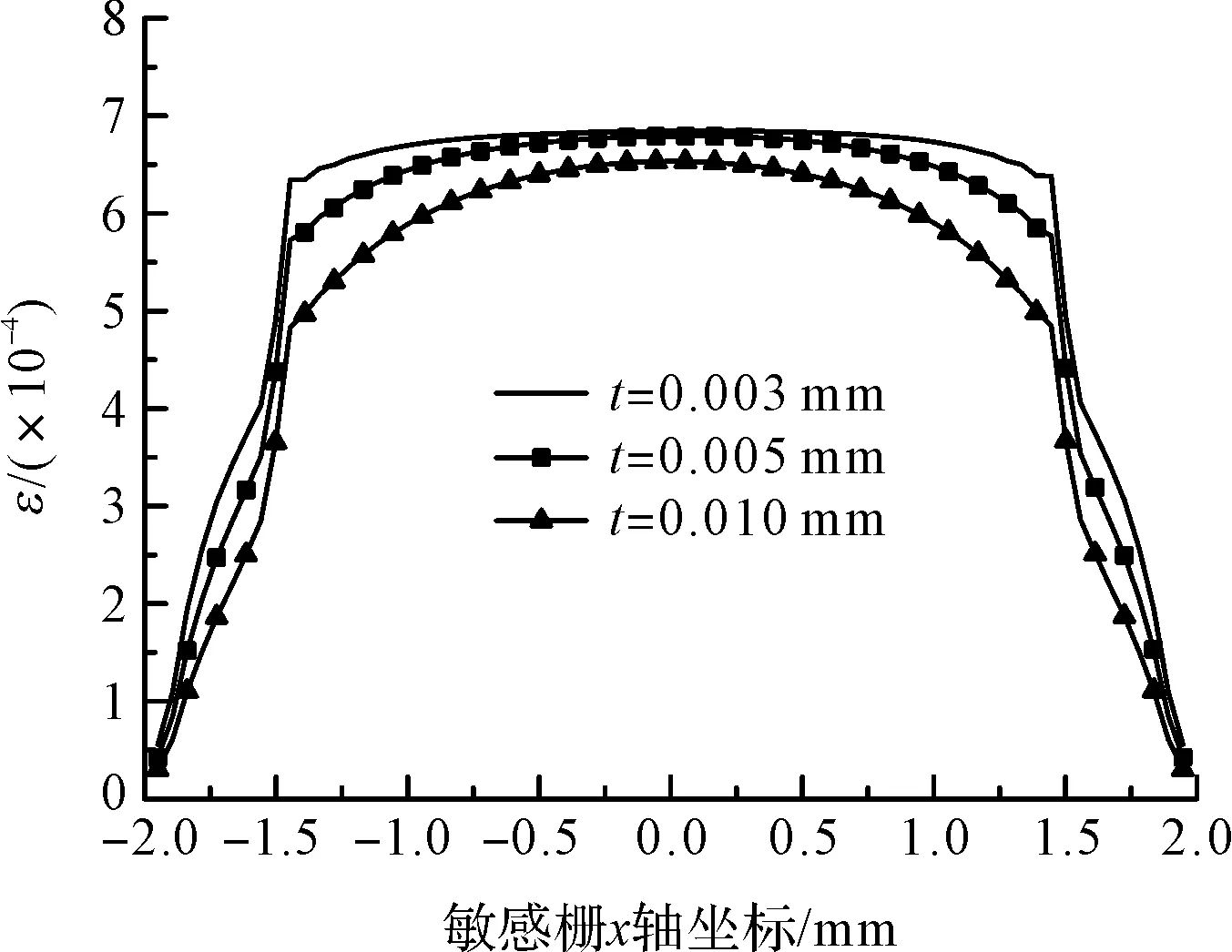
图9 不同敏感栅厚度敏感栅x方向应变分布

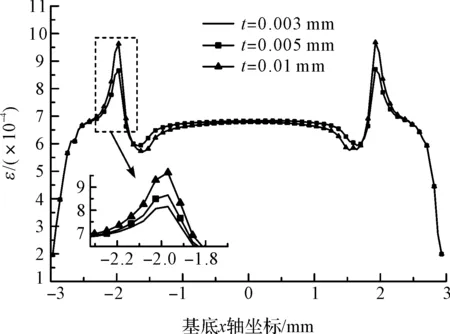
图10 不同敏感栅厚度基底x方向应变分布

从图上可以看出，敏感栅厚度对应变片应变分布影响很明显，敏感栅厚度越薄，栅丝上的应变分布越均匀，基底在应变突变区的x方向应变越小，即应变过渡区越小。

不同敏感栅厚度的应变传递误差如表3所示。

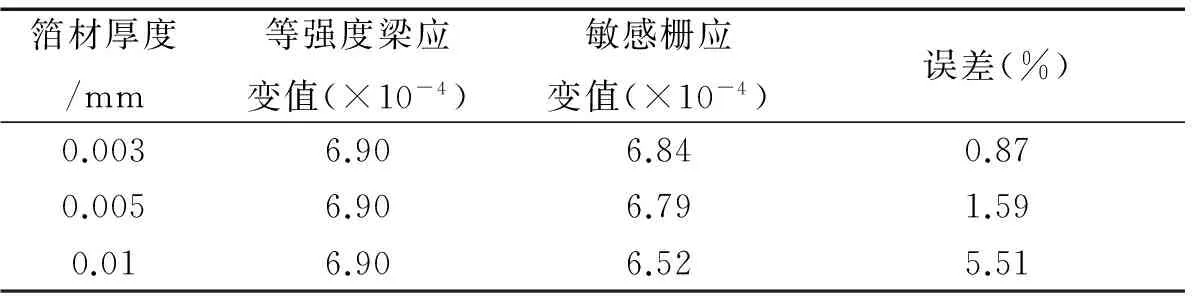
表3 不同敏感栅厚度的应变传递及误差

从表3中可以看出，箔材厚度为0.003 mm、0.005 mm、0.01 mm时应变传递误差分别为0.87%、1.59%、5.51%，厚度从0.003 mm增加到0.01 mm，误差增大了4.64%，应变传递误差随箔材厚度增加而增加，即敏感栅越薄越有利于应变传递。但是，由实际经验可知，应变片敏感栅越薄越容易损坏，因此应根据实际情况选择敏感栅厚度。

3.3 敏感栅栅丝长宽比

敏感栅栅丝长度和宽度决定了栅丝数目和应变片几何尺寸，为此本研究模拟了栅丝长宽比为：20∶1、50∶1和70∶1三种情况。不同敏感栅栅丝长宽比时敏感栅和基底的应变分布图如图11、图12所示。

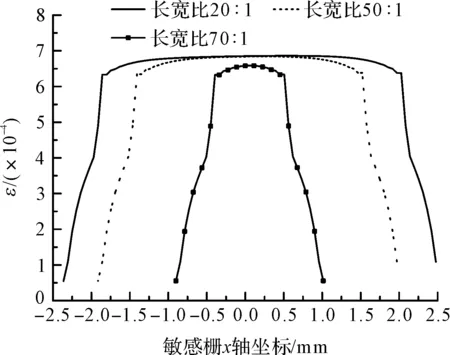
图11 不同栅丝长宽比敏感栅x方向应变分布

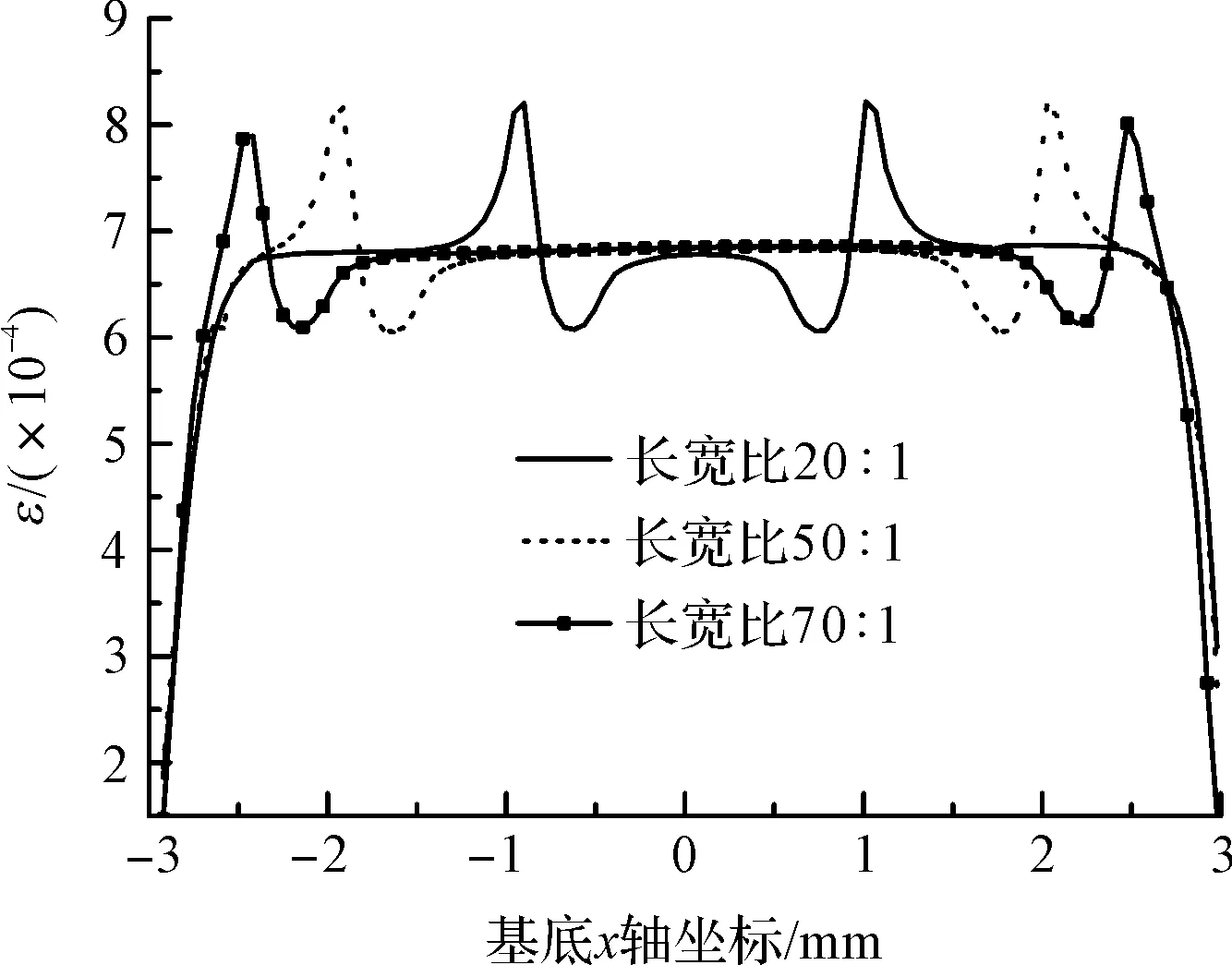
图12 不同栅丝长宽比基底x方向应变分布

从图上可以看出，长宽比越大，栅丝的应变分布越均匀，应变传递率越大。

不同栅丝长宽比时应变传递误差如表4所示。

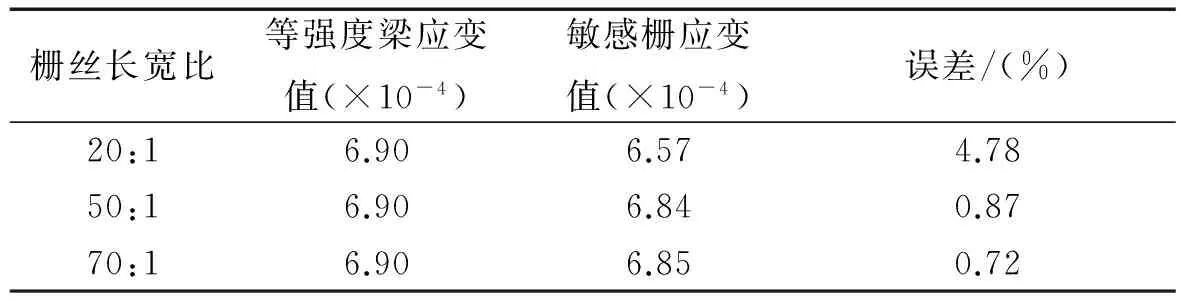
表4 不同栅丝长宽比的应变传递及误差

从表4中可以看出，栅丝长宽比为20:1、50:1和70:1时，应变传递误差分别为4.78%、0.87%、0.72%。长宽比从20:1增加到70:1时，误差减小了4.02%，在一定范围内，应变传递误差随长宽比增加而减少。该分析结果与文献[12]实验结果相一致。

3.4 敏感栅栅丝间距

当应变片栅丝长度一定时，栅丝间距越大，则敏感栅栅宽越宽。取栅丝间距h为0.056 mm、0.112 mm和0.28 mm，不同栅丝间距时敏感栅和基底的应变分布如图13、图14所示。

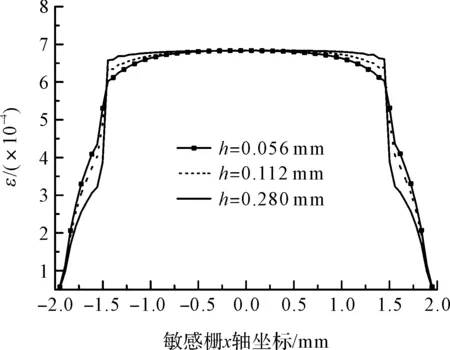
图13 不同栅丝间距敏感栅x方向应变分布

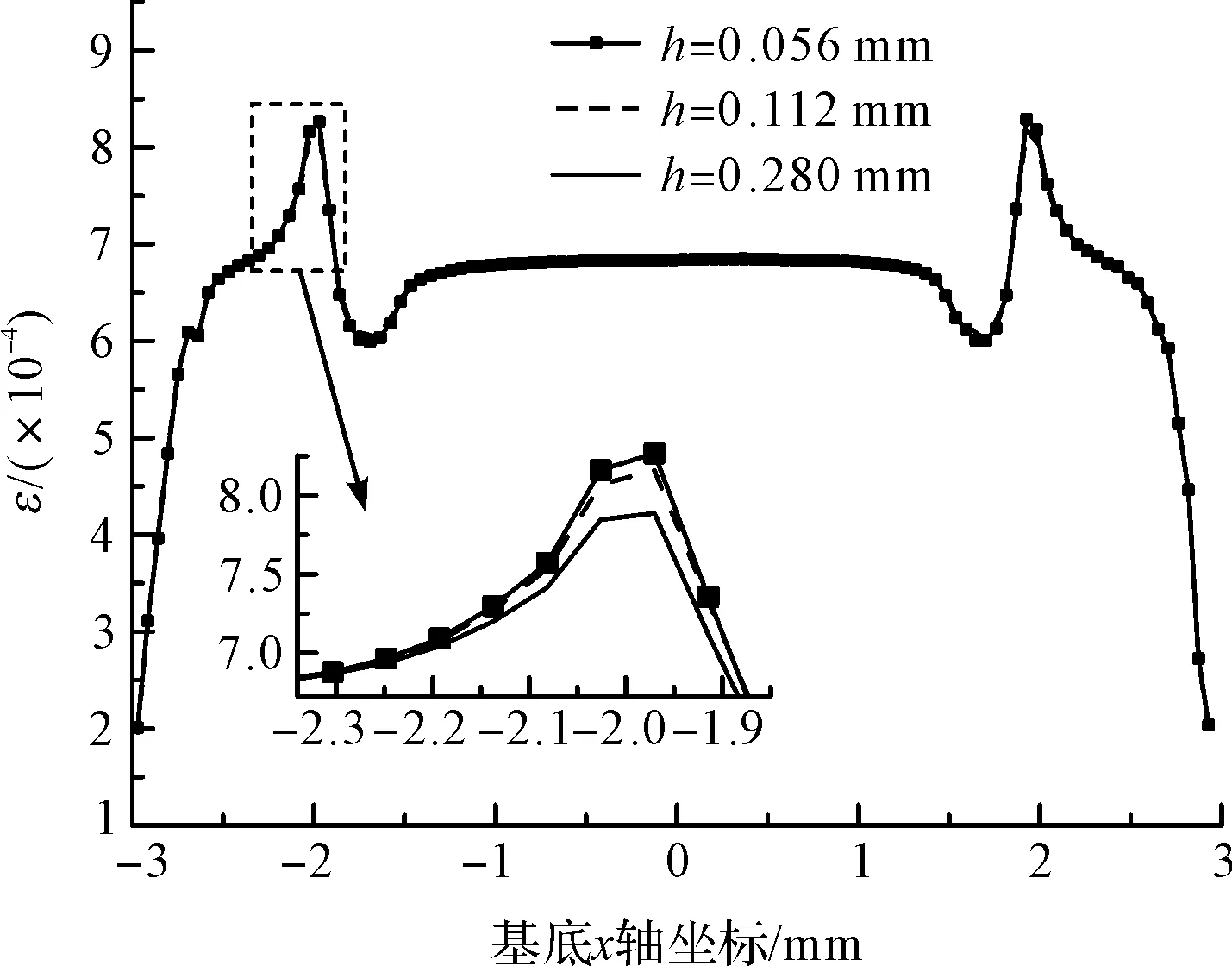
图14 不同栅丝间距基底x方向应变分布

从图上可以看出，栅丝间距越大，栅丝上的应变分布越均匀，基底应变突变区的x方向应变越小，即应变过渡区越小。

不同栅丝间距时应变传递误差如表5所示。

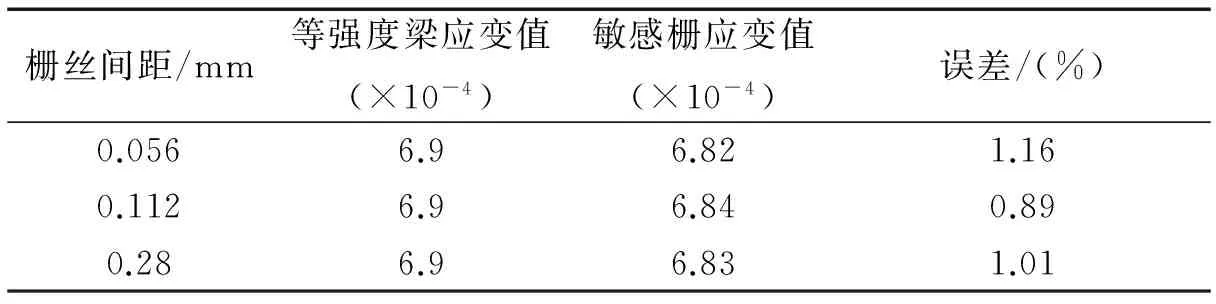
表5 不同栅丝间距的应变传递及误差

由表5可见，栅丝间距为0.056 mm、0.112 mm和0.28 mm时，应变传递误差分别为1.16%、0.89%、1.01%，栅丝间距从0.056 mm增大到0.112 mm时，应变传递误差减小了0.27%，而从0.112 mm增大到0.28 mm时，应变传递误差增加了0.12%，这说明栅丝间距存在最优值，该仿真结果与文献[12]实验结果相一致。

4 结束语

(1)本研究建立了等强度梁和应变片三维模型，通过有限元法模拟出的应变传递率达99.1%，可见该模型能正确地反映传感器的应变传递。从有限元结果可知，敏感栅的主要受力部位在测量栅中间位置，每根栅丝受力较均匀，并向两端逐渐递减至零。在应变传递过程中，基底与敏感栅之间存在应变过渡区；

(2)本研究分析了敏感栅材料、厚度、栅丝长宽比、栅丝间距变化时应变片应变分布规律及应变传递误差。研究表明：敏感栅材料弹性模量越小、厚度越薄，敏感栅的应变分布越均匀，基底在应变突变区的x向应变和切应变越小，即应变过渡区越小；栅丝长宽比越大，栅丝的应变分布越均匀。箔材弹性模量越小、厚度越薄和栅丝宽比越大，应变传递误差越小，越有利于应变传递，越能准确反映弹性体变形；敏感栅栅丝间距存在最优值；

(3)本文计算结果给出了敏感栅各结构参数对应变片应变分布和传递误差的影响，为电阻应变式传感器应变片的结构设计和应变片的选择提供了依据。

参考文献(References):

[1] FUYU W, FANG M. Factors influencing output non-linearity error of a high-precision load sensor and the error calculation[J].FiniteElementsinAnalysis&Design,2001,37(4):341-347.

[2] 韦铁平,杨晓翔,姚进辉,等.柱式负荷传感器的长径比对端部效应的影响[J].应用力学学报,2015,32(6):1038-1043

[3] 雷一鸣.电阻应变计应变传递研究及误差分析[J].科学技术与工程,2011(32):8096-8100.

[4] WEYMOUTH L J, STARR J, DORSEY J. Bonded resistancestraingages[J].ExperimentalMechanics,1979,19(3):112-120.

[5] YOUNIS N T, KANG B. Averaging effects of a strain gage[J].JournalofMechanicalScience&Technology,2011,25(1):163-169.

[6] SARANGI H, MURTHY K S R K, CHAKRABORTY D. Experimental verification of optimal strain gage locations for theaccurate determination of mode I stress intensity factors[J].EngineeringFractureMechanics,2013,110(1):189-200.

[7] 段 然,肖立峰.材料拉伸试验中影响应变片测量精度的因素分析[J].机械设计,2013,30(12):76-80.

[8] TANG K, SHA L, LI Y J, et al. Measurement of thermal expansion at low temperatures using the strain gage method[J].JournalofZhejiangUniversityenceA,2014,15(5):323-330.

[9] 张佳明,王文瑞,聂 帅.高温电阻应变片特性参数标定实验研究[J].中国测试,2014,40(5):25-28.

[10] ZIKE S, MIKKELSEN L P. Correction of gauge factor for strain gauges used in polymer composite testing[J].ExperimentalMechanics,2014,54(3):393-403.

[11] 王 彪,刘 腾,徐敬龙,等.金属粘贴式电阻应变计应变传递分析[J].中国测试,2016,42(8):1-6.

[12] 王文瑞,张佳明,聂 帅.高温应变接触式测量精度影响因素研究[J].固体火箭技术,2015(3):439-444.

[13] 胡玉梅,张方建,邵毅敏,等.应变片敏感栅结构参数对测量精度的影响[J].重庆大学学报:自然科学版,2013,36(12):21-27.

[14] 尹福炎.箔式应变片结构模型与有限元分析[J].衡器,2009,38(5):47-50.

[15] STEIN P. Strain gage history and the end of the twentieth century[J].ExperimentalTechniques,2010,25(2):15-16.

[16] 耿汉生.应变胶性能与应变计的工作特性[J].传感器用技术,1990(4):43-46.