基于响应面法的风机塔筒门框多目标优化研究

孟令锐，何海建，杨 扬，祝蕴龙，晁贯良，董姝言

(许昌许继风电科技有限公司，河南 许昌 461000)

0 引 言

风力发电机(以下简称风机)主要由叶片、齿轮箱、发电机、塔筒、基础等部分组成。塔筒作为风机的重要组成部分，承担着风机的大部分重量，并为风机运行提供足够强度、刚度等安全保障[1-2]。塔筒门框(以下简称门框)作为塔筒的一部分，位于塔筒底部靠近基础部分，主要供人员和设备进出。由于门框的存在改变了塔筒原有结构，使门框附近形状发生突变，存在应力集中现象，塔筒门框成为塔筒最易受到破坏的部位之一，因此很有必要对塔筒门框进行优化研究。

目前对于塔筒门框的分析，主流方法是有限元法。任瑞杰等[3]主要分析了塔筒门框的筋板厚度对门框的极限应力及其出现位置的影响，但仅选取了几个代表尺寸，忽略了筋板向内外拉伸厚度的影响。晏红文等[4]主要分析了门框形状参数、门框离地高度等对门框应力的影响，并对其进行了优化，但未考虑门框尺寸对其应力的影响。

本文主要基于GL2010规范[5]分析门框尺寸变化对其应力的影响，并对其进行优化分析。

1 有限元分析

1.1 有限元模型

塔筒模型坐标系根据GL2010规范进行确定。坐标原点在塔筒底部法兰下底面中心处，X轴由原点指向顺风向，Y轴由原点指向顺风向的左方，z轴由原点垂直指向塔筒上方，门框的开口位置为塔筒迎风面的正前方。

塔筒内部平台、爬梯、电缆支架等附属件对门框结构分析影响不大，在建模时对其进行简化处理。为了提高计算效率，根据圣维南原理[6]，本次计算仅建立包含门框的塔筒底段模型。

根据某3MW风力发电机组塔筒图纸，本研究在Workbench软件中建立塔筒底段的有限元模型。整个模型采用高阶六面体单元进行网格划分，在门框及其附近区域对网格进行细化处理，门框以外的区域适当地减小网格的密度。

门框及其附近区域网格划分如图1所示。

图1 门框及其附近区域网格划分示意图

1.2 材料性能

塔筒与门框均采用Q345E结构钢焊接成型，其弹性模量为2.1×1011Pa，泊松比为0.3，密度为7 850 kg/m3。根据GB/T 1591-2008《低合金高强度结构钢》[7]，材料属性如表1所示(根据GL2010规范，在进行零部件静强度计算时材料的安全系数应取为1.1)。

表1 材料Q345屈服强度表

1.3 边界条件

工程实践表明门框强度对弯矩载荷较为敏感，因此为了计算方便仅考虑载荷分量对门框及其附近区域应力分布的影响。施加完边界条件的塔筒模型如图2所示。

图2 施加完边界条件的塔筒模型

本研究根据GL2010规范，计算得到极限工况下塔筒顶部为1.934E8 Nm，载荷施加在塔筒顶部中心点，如图2中B点所示。对塔筒底部进行全约束，如图2中A点所示。

1.4 门框强度计算结果

经计算门框及其附近区域的最大等效应力为280.83 MPa，位于门框下底部门框筋板与筒壁结合处，应力云图如图3所示。

图3 门框等效应力云图

查表1可知当部件厚度为88 mm时，材料的屈服强度为305 MPa。材料极限强度安全系数计算公式如下：

(1)

式中:γf—载荷安全系数，取1.0；γm—材料安全系数，取1.1；σeqvmax—等效应力的最大值，MPa；Re—材料屈服强度，MPa。

经计算得到门框为0.987，无法满足设计要求，因此需要对门框结构进行优化来确保门框及其附近区域应力满足设计要求。

2 计算数学模型优化

要建立优化计算的数学模型需要先确定模型的设计变量、约束条件、优化目标。

2.1 设计变量

影响门框及其附近区域应力变化的因素众多，例如门框形状、门框离地高度、筒壁厚度等，本文仅假设在其他条件均不变的情况下，研究门框筋板厚度t1、筋板向外拉伸厚度h1、筋板向内拉伸厚度h2三者对门框及其附近区域应力的影响。因此本研究将t1、h1、h2设为优化设计变量，记为X=(t1,h1,h2)T。

各变量示意图如图4所示。

图4 门框设计变量示意图

各设计变量的优化取值范围如表2所示。

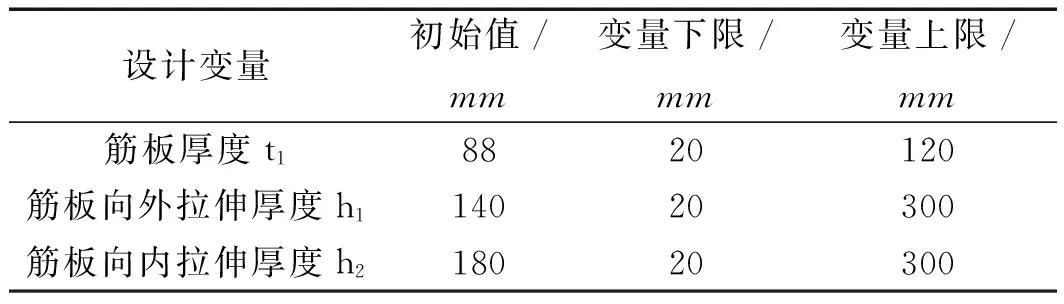
表2 设计变量取值范围

2.2 目标函数与约束条件

目标函数是判断优化方案优劣的数学表达式，通过找出目标函数的极值，从而找出最优的方案[8]。因门框的静强度无法满足设计要求，需要对塔筒门框及其附近区域的最大等效应力进行优化。同时在确保塔筒门框强度满足设计要求的前提下，为了降低门框的成本，也要对门框的质量进行优化。

由于门框筋板厚度在优化时是变化的，本研究为了保守起见，取其最大厚度120 mm计算得到其许用应力为259 MPa。优化目标是使门框及其附近区域的最大等效应力在不大于259 MPa情况下，尽量减小门框的等效应力和门框的质量。因此在优化时应将等效应力优化优先级设为最高，门框质量的优化优先级次之。

设等效应力的优化目标函数为F(X)，质量的优化目标函数为G(X)。

2.3 优化模型的数学表达式

构造好的优化模型数学表达式如下：

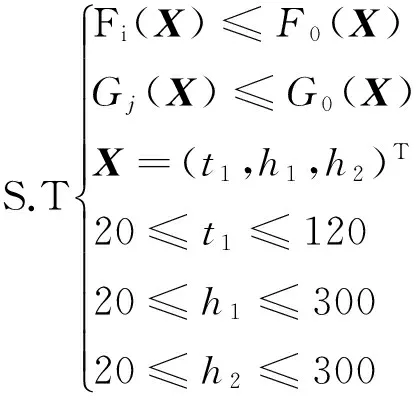
(2)

式中：F0(X)—门框许用等效应力；G0(X)—门框原始质量；Fi(X)—应力函数响应值，i=1,2,……n；Gj(X)—质量函数响应值，j=1,2,……n；n—样本个数。

3 响应面分析

响应面法(response surface method， RSM)是通过对设计点的试验分析得到目标函数在约束条件下的响应面模型，并以此来预测非设计点响应值的方法[9]。在工程应用当中，响应面模型一般采用二阶多项式来表达[10]，其数学表达式如下：

(3)

式中；y(x)—响应值；xi—设计变量，i=1,2,……,k；β0，βi，βii，βij—待确定的回归系数，可以通过最小二乘法来估计多项式的回归系数β。

3.1 实验设计(DOE)

样本点选取对构造的响应面模型精确度影响很大，因此需要一个很好的实验设计来确保样本点选取的合理性。本文采用Workbench实验设计中的中心复合实验设计(CCD)来选取样本点，该算法能够在二阶实验设计阶段重复利用一阶实验设计，它以最小的实验循环提供了诸多设计变量与实验误差之间的相关信息，从而以最少的样本数量来建立响应面模型[11]，节约了计算时间。CCD实验设计结果如表3所示。

表3 CCD实验设计结果

根据实验设计结果，通过最小二乘法计算出式(3)的回归系数矩阵，构建各响应值的二次多项式响应面函数如下：

G(X)=1.49+0.0214t1+0.000 9h1+0.000 8h2+

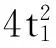
(4)

F(X)=0.225 9-0.117 1t1+0.057 6h1-0.085 1h2+

0.811 8t1h1+3.134 4t1h2+0.526 7h1h2-

(5)

3.2 响应面模型检核

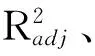
(6)

(7)

(8)

(9)

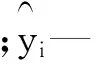
利用式(6,9)对响应面模型进行方差分析，计算结果如表4所示。

表4 响应面模型显著性校核结果

3.3 响应面分析

经响应面分析，得出各设计变量在变化区间内与目标函数之间的相应关系。由于主要考察的是设计变量与门框的最大等效应力之间的关系，而质量只是一个次要的优化目标，本文只研究各设计变量之间交互作用对门框最大等效应力的影响。t1、h1交互作用对等效应力的影响如图5所示。

图5 t1、h1交互作用对等效应力影响

t1、h2交互作用对等效应力的影响如图6所示。

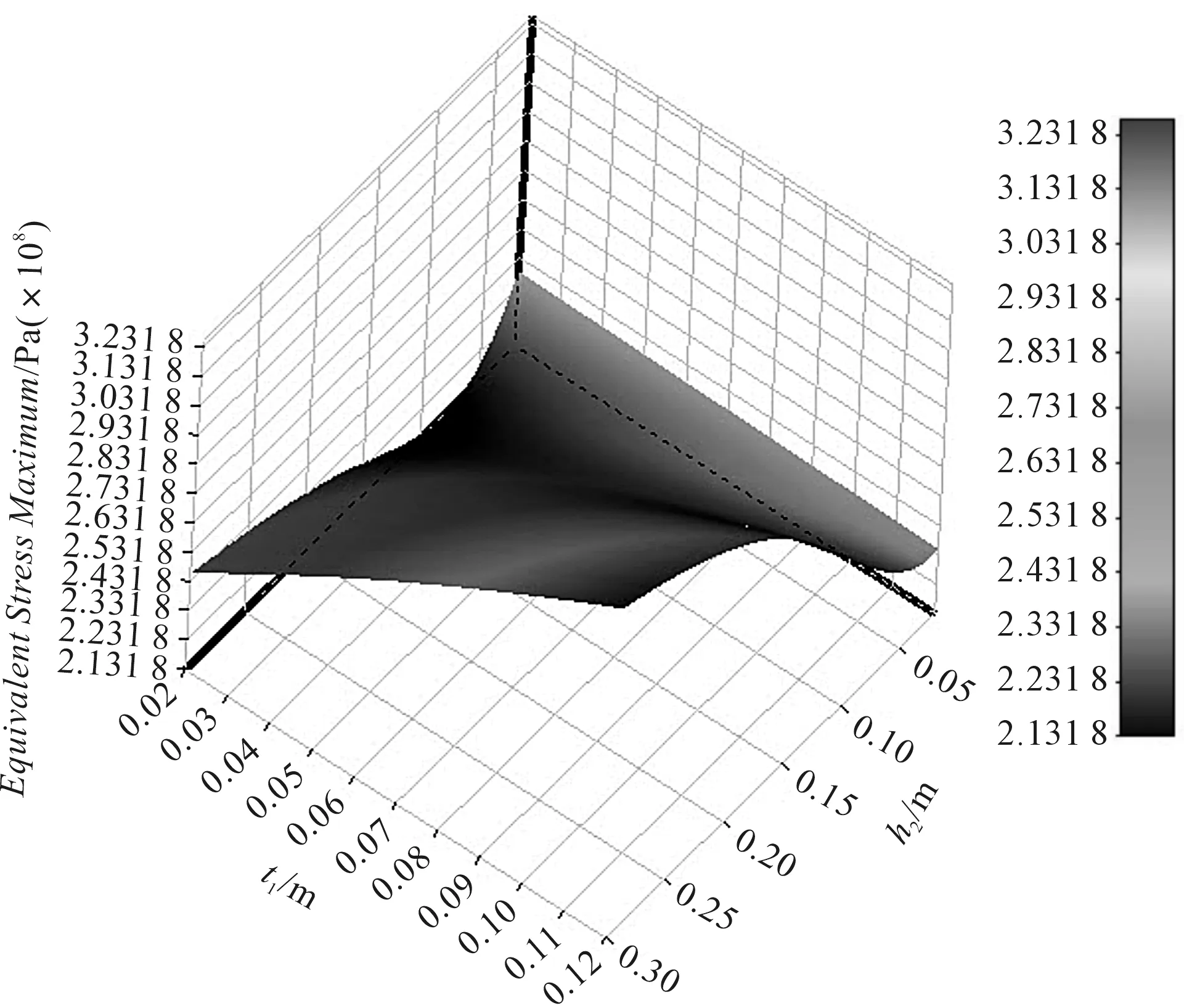
图6 t1、h2交互作用对等效应力影响

h1、h2交互作用对等效应力的影响如图7所示。

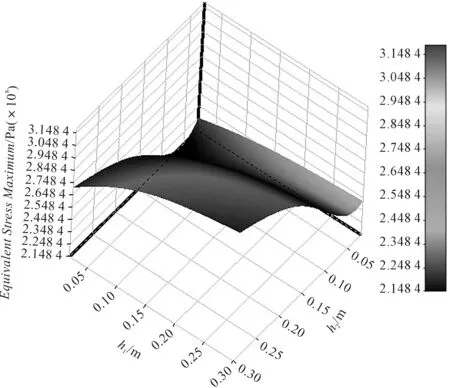
图7 h1、h2交互作用对等效应力影响

可以看出，3个设计变量之间的交互作用当中，筋板厚度t1与筋板向内拉伸厚度h2的交互作用对等效应力的影响最大，筋板向内拉伸厚度h2与筋板向外拉伸厚度h1的交互作用对等效应力的影响次之，筋板厚度t1与筋板向外拉伸厚度h1的交互作用对等效应力的影响最小。后续在对门框进行优化时，可以优先针对筋板厚度和筋板向内拉厚度进行调整。分析表明，随着设计变量值的增加，筋板厚度t1、筋板向外拉伸厚度h1与门框所受最大等效应力之间的函数关系为单调递增的凸抛物线形式，而筋板向内拉伸厚度h2与门框所受最大等效应力之间的函数关系为凹抛物线形式。t1所对应的等效应力变化幅值是最大的，单个变量与门框所受最大等效应力之间的函数关系式会随着其他两个变量的改变而变化。

4 灵敏度分析

灵敏度分析是指关注的变量对整体结构响应的影响程度，数值越大影响越大。这样可以为后续提供一个有效的优化思路，当要控制结构的响应时，可以改变对此结构响应灵敏度较大的变量来快速实现。门框及其附近区域最大等效应力对各设计变量变化的灵敏度如图8所示。

图8 门框灵敏度分析结果

由图8可知，对门框及其附近区域等效应力最大值影响最大的是塔架门框厚度t1，筋板向内拉伸厚度h2次之，筋板向外拉伸厚度影响最小。同时可以发现门框的等效应力敏感度分析结果与响应面分析的结果基本一致，这也说明了响应面模型可靠有效。

5 基于遗传算法的多目标优化

对于多目标优化问题，各优化目标之间一般不能够同时达到最优，因此得出来的是一系列的有效解，此类解称为pareto解[14-15]。多目标优化问题就是在一系列的pareto解当中找到最有效的几个解，之后根据实际工程需要，从中再选出最满意的解。本文基于多目标遗传算法(MOGA)，利用Workbench软件中目标驱动优化(GDO)模块，根据2.2节制定的优化目标函数及优先级，对目标函数进行优化求解。

经过优化，得出的3组最优pareto解如表5所示。

表5 3组最佳候选设计点

由表5可知，虽然候选点1的门框质量与等效应力都是最小的，但考虑到制造因素与实用性等原因，应选取候选点2作为最优设计点。

将候选点2数据进行圆整并作为最优设计点，对该设计参数下的门框进行静强度计算，优化前后结果如表6所示。

表6 优化前后结果对比

由表6可知，优化后的门框质量减少73.82%，门框最大等效应力减小26.69%，门框的极限强度SRFext为1.48，优化后门框性能指标有所加强。

6 结束语

本研究通过Workbench软件建立了风机塔筒有限元模型，对其进行静力分析得到了门框原始力学性能；采用中心复合实验设计方法建立门框优化的响应面模型，回归计算证明其具有很高的拟合度；通过响应面分析方法研究了门框尺寸变化对其所受等效应力的影响。

研究结果表明：随着设计变量值的增加，筋板厚度t1、筋板向外拉伸厚度h1与门框所受最大等效应力之间的函数关系为单调递增的凸抛物线形式，而筋板向内拉伸厚度h2与门框所受最大等效应力之间的函数关系为凹抛物线形式，结果与工程实际相吻合。

基于响应面分析结果，本文运用遗传算法对门框进行了多目标优化。优化结果表明：优化后的门框质量减少73.82%，门框最大等效应力减小26.69%，门框的极限强度SRFext为1.48，表明优化是有效的。

参考文献(References):

[1] 丁小川，李 忆，吕渤林，等.大型风电机组塔架门洞结构强度分析与优化[J].机械制造，2014，49(11):34-36.

[2] 朱锴年.风力发电机组塔架制造工艺与质量控制[J].机电工程技术，2016，45(10)：136-140.

[3] 任瑞杰，王 林，麻 磊，等.影响风机塔筒门设计的主要因素[J].现代机械，2011(6):45-47.

[4] 晏红文，田红旗，梁裕国，等.基于Isight的塔架门框结构的优化设计[J].机械强度，2015，37(4):646-650.

[5] Germanischer Lloyd. Rules and guidelines IV Industrial Services Part I: guideline for the certification of wind turbines[M]. Hamburg: Germanischer Lloyd,2010.

[6] 徐芝纶.弹性力学[M].北京：高等教育出版社，2006.

[7] GB/T 1591-2008.低合金高强度结构钢[S].北京：中国标准出版社，2008.

[8] 蔡 新，郭兴文，张旭明，等.工程结构优化设计[M].北京：中国水利水电出版社，2003.

[9] 胡俊峰，徐贵阳，郝亚洲，等.基于响应面法的微操作平台多目标优化[J].光学精密工程，2015,23(4):1096-1103.

[10] 王永菲，王成国.响应面法的理论与应用[J].中央民族大学学报:自然科学版，2005,14(3):236-239.

[11] 李 莉，张 赛，何 强，等.响应面法在试验设计与优化中的应用[J].实验室研究与探索，2015,34(8):41-45.

[12] 吕 辉，于德介，谢 展，等.基于响应面法的汽车盘式制动器稳定性优化设计[J].机械工程学报，2013,49(9):55-30.

[13] 代 翠，孔繁余，董 亮，等.基于响应面法的离心泵作透平水力和声学性能优化[J].农业工程学报，2015,13(15):40-46.

[14] 姜 衡，管贻生，邱志成，等.基于响应面法的立式加工中心动静态多目标优化[J].机械工程学报，2011,47(11):125-132.

[15] 魏心友，曾国辉，王卫军.基于ABAOUS及modeFRONTIER的多目标优化方法[J].轻工机械，2016，34(1)：59-63.