基于粒子群遗传算法的城市轨道交通列车折返时刻表优化研究

孙 旺

SUN Wang

（中国铁道科学研究院 研究生部，北京 100081）

(Postgraduate Department， China Academy of Railway Sciences， Beijing 100081， China)

挖掘城市轨道交通线路的最小运营间隔问题一直是困扰运营商和信号供应商的一个难题，而终端折返方式通常是影响运营间隔的最主要因素。为此，将最优化算法、列车控制曲线和实际站型相结合，从选择最优终端折返方式的角度出发，运用粒子群遗传算法，实现用计算机自动获取终端站折返方式的最优解，从而为探寻最小运营间隔，以及编制最小运营间隔时刻表找到一条可行之路。

1 概述

1.1 典型的终端站型及其进出站过程

终端折返一般分为站前折返和站后折返 2 种方式，每种折返方式又分为单渡线折返和交叉折返，其中，交叉折返时采用不同的进出站过程，折返时间又不尽相同。以站前交叉折返方式为对象进行折返能力的最优化研究。城市轨道交通线路中一种典型终端站型示意图如图 1 所示，该站型进出站方式的折返过程示意图如图 2 所示。

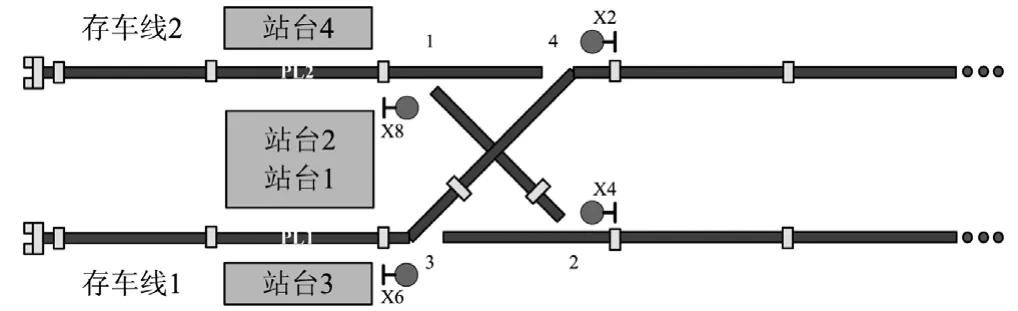
图 1 一种典型终端站型示意图Fig.1 A typical terminal station

从图 2 可以看出，进站过程 A，开放信号机X2 至信号机 X6 的进路，让列车侧向运行，进入下行站台轨 PL1；进站过程 B，开放信号机 X2 至信号机 X8 的进路，让列车直向运行，进入上行站台轨PL2；出站过程 H，开放信号机 X6 至信号机 X4 的进路，让列车直向运行，从站台轨 PL1 出站；出站过程 I，开放信号机 X8 至信号机 X4 的进路，让列车侧向运行，从站台轨 PL2 出站[1]。

1.2 折返能力分析

折返能力是指单位时间内折返车站能够完成折返作业的最大列车数，单位时间一般以 1 h 计量，如果用Ttb表示车站的平均折返间隔时间，ntb表示每小时内的折返列车数，则折返能力的计算公式可以表示为

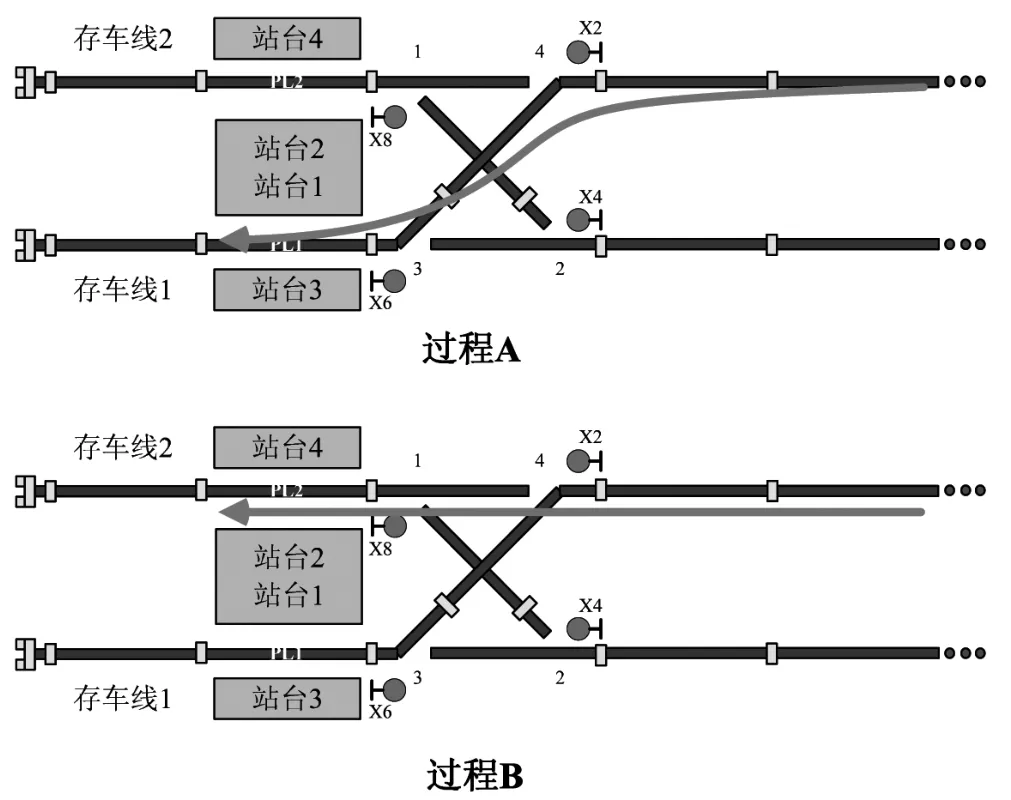
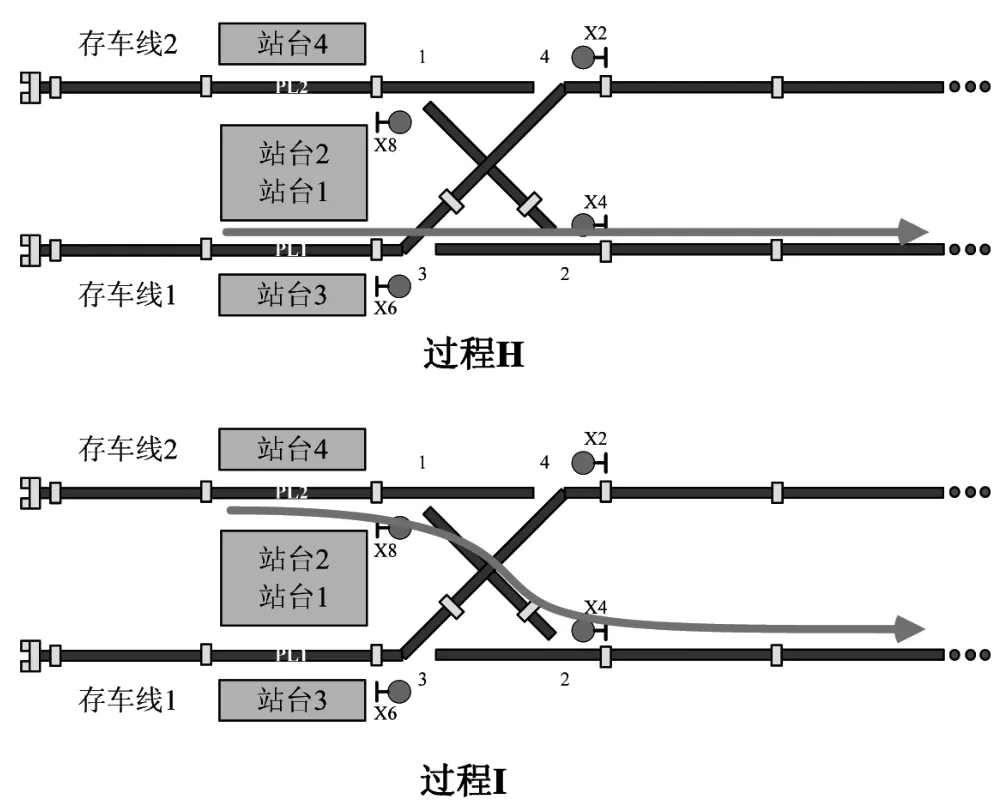
图 2 折返过程示意图Fig.2 Schematic diagram of different turnback processes

1.2.1 单站台折返能力分析

单站台折返即固定使用单一站台轨进行列车折返作业，通常有 2 种单站台折返方式：①只使用站台轨 PL1 进行折返，即由 A-H-A 过程组合而成；②只使用站台轨 PL2 进行折返，即由 B-I-B 过程组合而成。经过现场测算，以上 2 种方式的折返间隔近似相等，折返间隔时间Ttb在 155 s 左右，因而上述站型的单站台折返能力为ntb= 3 600 /Ttb=23 列/h。

1.2.2 双站台折返能力分析

双站台折返即分别交叉使用 2 个站台轨进行车站折返的作业过程，该过程比较复杂，以前后列车不连续进入同一站台，交叉渡线的进路开放满足联锁条件为前提，双站台折返方式按照过程 A，B，H，I 的组合可以划分为方式 1 (A-B-I-H-A)、方式 2 (A-B-H-I-A)、方式 3 (A-I-B-H-A)、方式 4 (A-I-H-B-A)、方式 5 (A-H-B-I-A)、方式 6(A-H-I-B-A) 6 种方式。

考虑站型和联锁条件，列车完成 A，B，H，I 中每个过程的走行时间都会受到进路开放时机、停站时间、司机响应时间、各种设备延时等因素的制约，完成上述双站台折返的所有折返方式手工分析，并找到一种折返能力最高的折返方式，计算量巨大，并且容易出错。因此，借鉴最优化理论，使用粒子群遗传算法，将人工进行的折返分析转化为计算机自动寻优。

2 基于粒子群遗传算法的折返方式寻优

2.1 粒子群遗传算法

Eberhart 和 Kennedy 于 1995 年提出了标准粒子群算法 (Particle Swarm Optimization，PSO)。该算法的灵感来源于鸟类的觅食过程，假设只有一小片谷物，一群鸟虽然不知道食物的确切地点，但通过个体的搜索和群鸟间的信息共享，根据自身所经历过的最佳位置和鸟群所经历过的最佳位置来判断食物的可能方位，并各自调整飞行方向和速度，最终群鸟都可以聚拢到食物的所在地。

标准粒子群算法将鸟群寻食过程转化成了一个寻找最优解的算法：将单个鸟所在位置看作是d维搜索空间中的一个点，称之为粒子；粒子所在位置的优劣由一个适应度函数来决定[2]；根据所有粒子可以算出一个群体最优位置；粒子根据自身的移动轨迹可以算出一个自身历史最优位置；每个粒子都根据群体最优位置和自身历史最优位置来调整自己的运动方向和速度，从而实现所有粒子在解空间内向最优位置的靠拢。

标准粒子群算法的位置和速度更新公式可以表示为

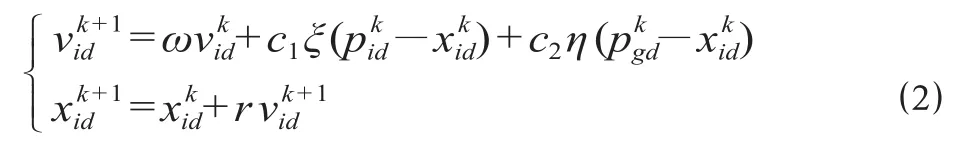
标准粒子群算法的计算机编程实现流程一般为：①初始化粒子种群，设置种群中每个粒子的位置、速度等初始值；②根据适应度函数计算群体最优值和单体的历史最优值；③根据粒子群算法的位置和速度公式更新位置和速度；④进行适应度评估，计算群体最优值和历史最优值；⑤判断是否满足终止条件，满足则寻优过程结束，不满足则继续重复步骤③到⑤。

标准粒子群算法是一种智能化的寻优算法，但其只依据自身的历史最优值和全局最优值来调整每个粒子的位置，这样会造成当历史最优值和全局最优值是局部最优解时，整个算法过早收敛，从而产生早熟的问题。为了克服该问题，后期又演化出了粒子群遗传算法。

在粒子群遗传算法中，一方面引入了遗传算法中的变异算子对粒子群中部分粒子的位置进行随机变异操作[4]，防止粒子群陷入局部最优，以提高算法的抗早熟性；另一方面引入了遗传算法中的克隆选择算子，根据“优胜劣汰，适者生存”的原则[5]，通过粒子个体的适应度来确定个体的生存，使粒子群的平均适应度不断提高，增强粒子群对局部的搜索能力，可以在局部加快收敛，提高算法效率。

计算机编码实现时，与标准粒子群算法流程相比，粒子群遗传算法主要是在步骤③和步骤④之间增加一个克隆变异过程：遴选劣等粒子进行变异操作，遴选优等粒子进行克隆操作，其他部分与标准粒子群算法的流程相同。

2.2 折返寻优的算法结合

粒子群遗传算法和终端站折返结合的关键在于以什么作为粒子，即d维位置向量xi= (xi1，xi2，…，xid) 的含义，以及适应度函数的评判原则。以终端折返方式 1 (A-B-I-H-A) 为例，通过分析每个子过程的时间消耗情况对d维位置向量的选取和适应度函数的设计进行说明。

（1）子过程 A。该过程是从站 2 的上行站台发车，开放信号机 X2 至信号机 X6 的进路，让列车侧向运行，进入站 1 的下行站台轨 PL1 的进站过程。进站过程 A 的速度曲线如图 3 所示。

图 3 中，“曲线 1”表示当信号机 X2 到信号机 X6 的进路已提前开放，列车从站 2 出站，进入站 1 的过程中速度曲线不受信号机红灯影响的情况。“曲线 3”表示当信号机 X2 开放较晚，由于列车自动防护系统 (ATP)/列车自动驾驶系统 (ATO) 的作用，列车自动在红灯信号机前停车后信号机X2 才开放的进站情况，其中P0点为列车开始降速的位置；P2为列车制动到停车的位置；P1为列车加速到最高运行速度的位置。“曲线 2”表示信号机 X2 到信号机 X6 的进路开放较晚，影响列车减速但未造成列车停车的情况。

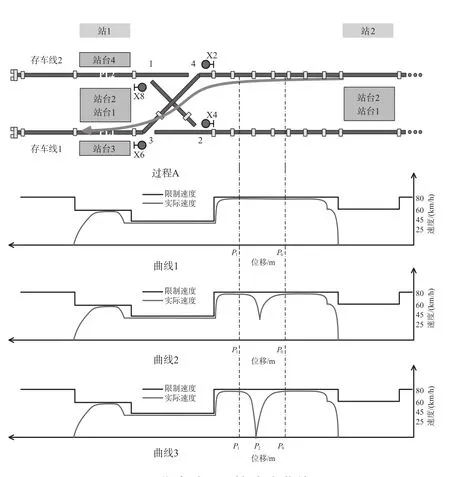
图 3 进站过程 A 的速度曲线图Fig.3 The speed curve of process a to enter the station

由图 3 可以看出，信号机 X2 到信号机 X6 进路开放的时机会影响列车完成过程 A 所消耗的时间，而且耗时的差异集中在P0点到P1点这段距离的行驶时间上。假设P0点到P1点的距离为S01，以折返方式 1 开始的时刻 (即列车从站 2 发车时) 为时间原点[6]，列车从站 2 发车后t1秒时，信号机 X2 到信号机 X6 的进路开放，则列车从P0点到P1点的走行时间函数可用分段函数表达为

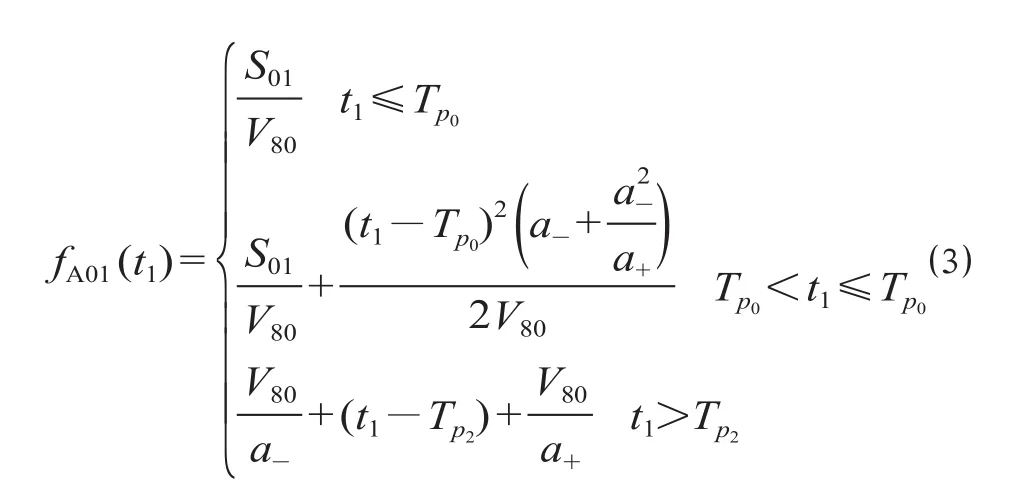
式中：fA01(t1) 为列车从P0点到P1点的走行时间函数；Tp0为列车从站 2 发车到P0点所经历的时间；Tp2为列车从站 2 发车到P2点停稳的时间；V80为限速 80 km/h 工况下列车的最高行驶速度；a-为 ATO降速时用的减速度；a+为 ATO 加速时用的加速度。

公式 ⑶ 与图 3 中曲线的对应关系是：t1≤Tp0情况下的函数式是对列车按图 3 中曲线 1 的方式从P0点到P1点的走行时间描述；Tp0＜t1≤Tp2情况下的函数式是对曲线 2 的描述；t1＞Tp2情况下的函数式则是对曲线 3 的描述。分析整个进站过程 A，用TAL表示列车在P0-P1区域外的走行时间，则列车完成过程 A 需要的时间可以表示为

（2）子过程 B。该过程是从站 2 的上行站台发车，开放信号机 X2 至信号机 X8 的进路，让列车直向运行，进入站 1 的上行站台轨 PL2 的进站过程。仍然以子过程 A 中的列车 1 从站 2 发车的时刻为子过程 B 的时间原点；t2为列车 2 从站 2 发车的时刻；t3为信号机 X2 到信号机 X8 的进路开放的时刻；TASC为列车 1 从P1点按过程 A 进站到完全出清岔区的走行时间；TRC为从触发进路到进路完全办理成功的时间。由于造成列车减速的都是 X2 信号机，因而P0，P1，P2点的位置与 A 过程完全相同，可得列车 2 从P0点到P1点的走行时间函数可以表示为

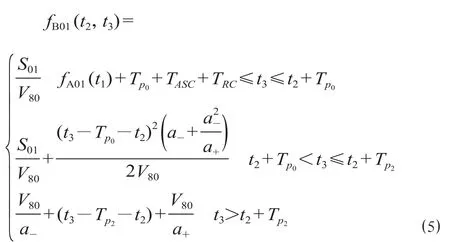
用TBL表示列车在完成过程 B 时在P0－P1区域外的走行时间，则列车完成过程 B 的时刻为

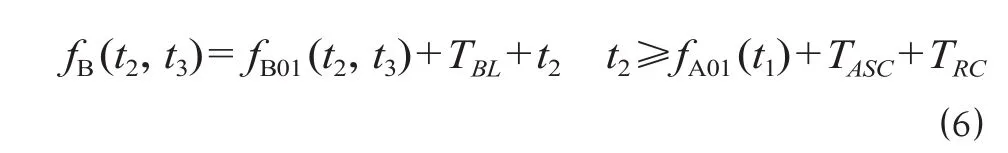
（3）子过程 I。该过程是从站 1 的上行站台轨PL2 发车，开放信号机 X8 至信号机 X4 的进路，让列车侧向出站的过程。t4为列车 2 在 2 轨站台的停车时间[7]；TISC为列车 2 从站台轨 PL2 发车到完全出清岔区的走行时间。对于出站过程，按照出站进路排列完成时，列车即立即发车的方式分析，则列车 2 执行出站过程 I 至完全出清岔区的时刻为

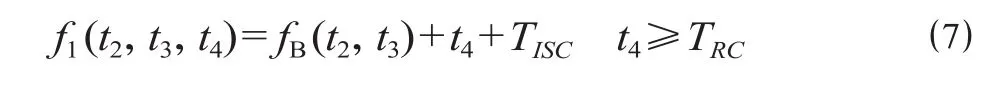
（4）子过程 H。该过程是从站 1 的下行站台轨PL1 发车，开放信号机 X6 至信号机 X4 的进路，让列车直向出站的过程。t5为列车 1 在 1 轨站台的停车时间；THSC为列车 1 从站台轨 PL1 发车到完全出清岔区的走行时间[8]。对于出站过程，按照出站进路排列完成时，列车即立即发车的方式分析，则列车1执行出站过程 H 至完全出清岔区的时刻为

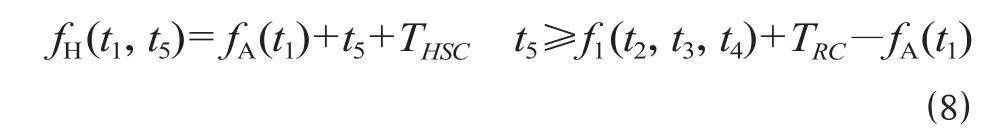
综上分析可见，可以选取t1，t2，t3，t4，t5作为折返方式 1 (A-B-I-H-A) 的 5 维位置向量，ti= (t1，t2，t3，t4，t5)。其中：t1为 A 过程中信号机 X2 到信号机 X6 的进路开放时刻，取值范围为t1≤Tp0，Tp0＜t1≤Tp2，t1＞Tp23 个区间；t2为 B 过程中列车 2 从站 2 发车的时刻，取值范围为t2≥fA01(t1) +TASC+TRC；t3为B过程中信号机X2到信号机X8的进路开放的时刻，取值范围为fA01(t1) +Tp0+TASC+TRC≤t3≤t2+Tp0，t2+Tp0＜t3≤t2+Tp2，t3＞t2+Tp23 个区间；t4为 I 过程开始前列车 2 在站 1 的站台轨 PL2 的停车时间，取值范围为t4≥TRC；t5为 H 过程开始前列车 1 在站 1 的站台轨 PL1 的停车时间，取值范围为t5≥fI(t2，t3，t4) +TRC－fA(t1)。此外，综合考虑折返时间短、停站时间长时更有力于运营，并分别分配折返时间权重因子d1和停站时间权重因子d2[9]，则适应度函数设置为

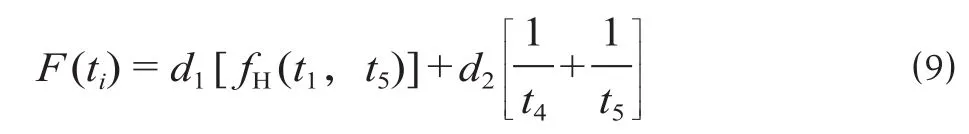
3 仿真验证

根据现场测算和考虑延时，选取程序中用到的参数：从触发进路到进路完全办理成功的时间参数TRC为 13 s (需要转动道岔) 和 3 s (不需转动道岔)；列车在完成过程 A 时在P0到P1区域外的走行时间参数TAL为 111 s；列车在完成过程 B 时在P0到P1区域外的走行时间参数TBL为 98 s；列车从站 2 发车到P0点所经历的时间参数Tp0为 43 s；过程 A 列车从P1点到完全出清岔区走行时间参数TASC为 62 s；P0点到P1点的距离S01为 942 m；列车按 I 过程从2 轨站台发车到完全出清岔区的走行时间参数TISC为 34 s；列车按 H 过程从 1 轨站台发车到完全出清岔区的走行时间参数THSC为 24 s。

编制程序：通过配置文件将 6 种折返方式需要的粒子向量初始值、描述参数、适应度评价函数及粒子群遗传算法的参数写入文件，程序启动时通过读取文件的方式初始化相应变量。其中，设置粒子群中的粒子个数为 100；最大迭代次数为 1 000；c1和c2均选用 2.5；惯性权重ω取初值为 0.9，取值范围为 0.2～0.9；随机变异算子为 0.01，取值范围为 0～0.02；克隆选择算子为 0.1，取值范围为0.01～0.2；折返间隔最短的权重d1设置为 0.8；停站时间尽量长的权重d2设置为 0.2。

编制粒子群遗传算法，使用轮盘算法来挑选需要克隆和变异的粒子，选择适应值更贴近全局最优值的粒子进行克隆操作，选择适应值更远离全局最优值的粒子进行变异操作[10]。通过粒子群遗传算法获得每种折返方式的最优解，再将所有折返方式的最优解进行横向对比，最终得出最优的折返方式和其对应的最优解。仿真验证程序流程图如图 4 所示。

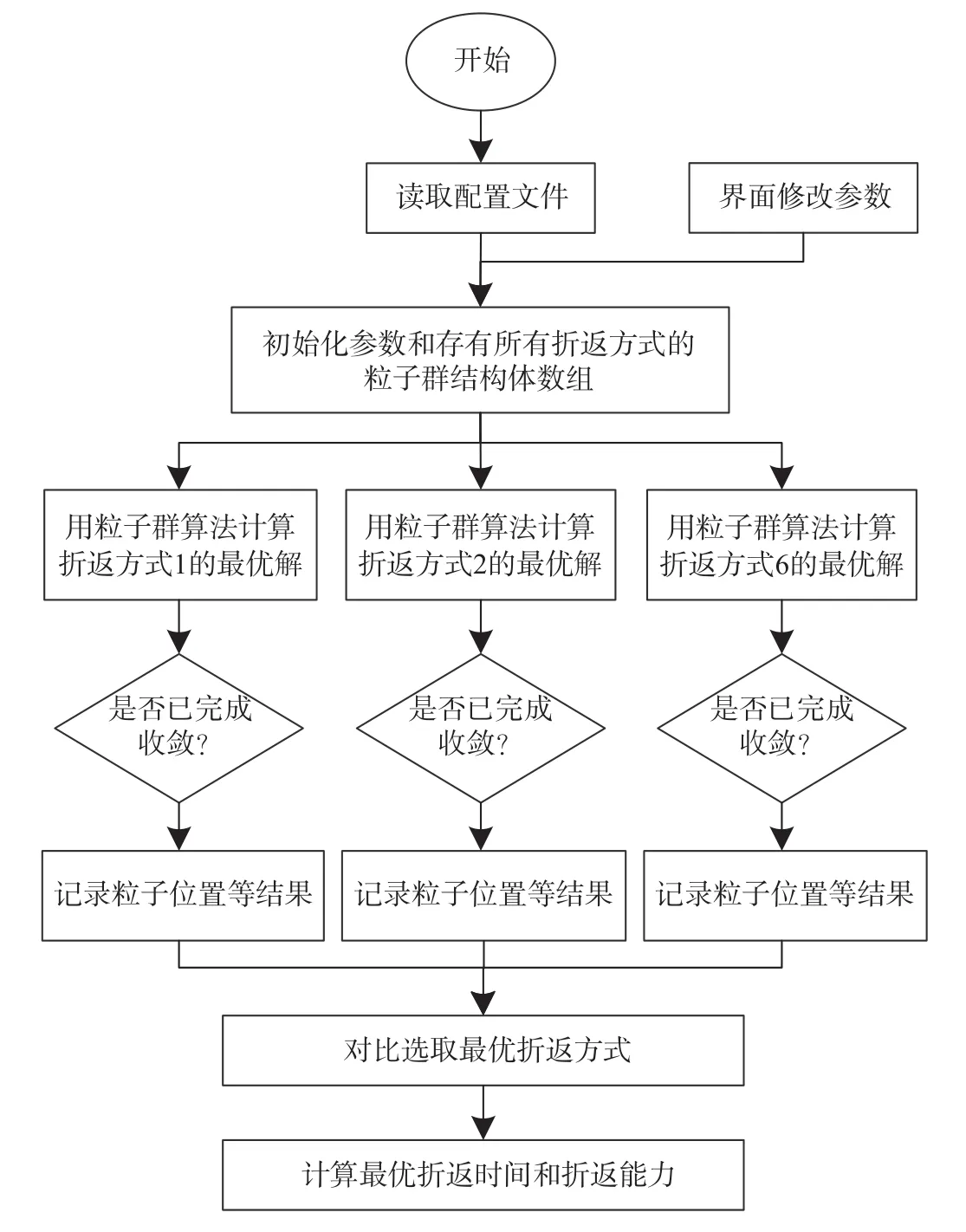
图 4 仿真验证程序流程图Fig.4 The flow chart of simulation program

通过程序调试和参数调整，使程序对每种折返方式均可在 120 次迭代的时候收敛到其最优折返时间上，各种方式折返寻优收敛如图 5 所示，寻优计算结果统计表如表 1 所示。

通过综合分析停站过程，对站台有车情况进行统计，站台有车示意图如图 6 所示。

在图 6 中深色的为站台有车，否则为站台无车，显然折返方式 3 的站台有车情况要优于折返方式 4，在折返方式 3 中，整个折返过程中都有车在站台停站，有效地方便了乘客出行。因此，在程序的对比选择模块中，对计算结果进行站台有无车的标识。首先，仿照光栅效果，对折返的全过程时间段进行 100 份等分处理。然后，对等分出来的每个时刻的站台有无车情况进行函数标识，focp(tj) 为tj时刻有无车情况的标记函数，有车时focp(tj) 为 2，无车时为 1。最后，对整个折返过程的终端站有车情况进行数值统计，统计公式可以表示为

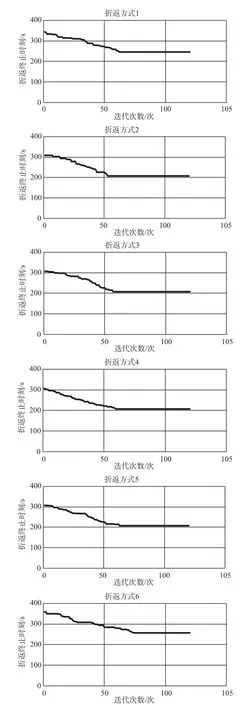
图 5 折返寻优收敛图Fig.5 Optimization convergence diagram of turnback

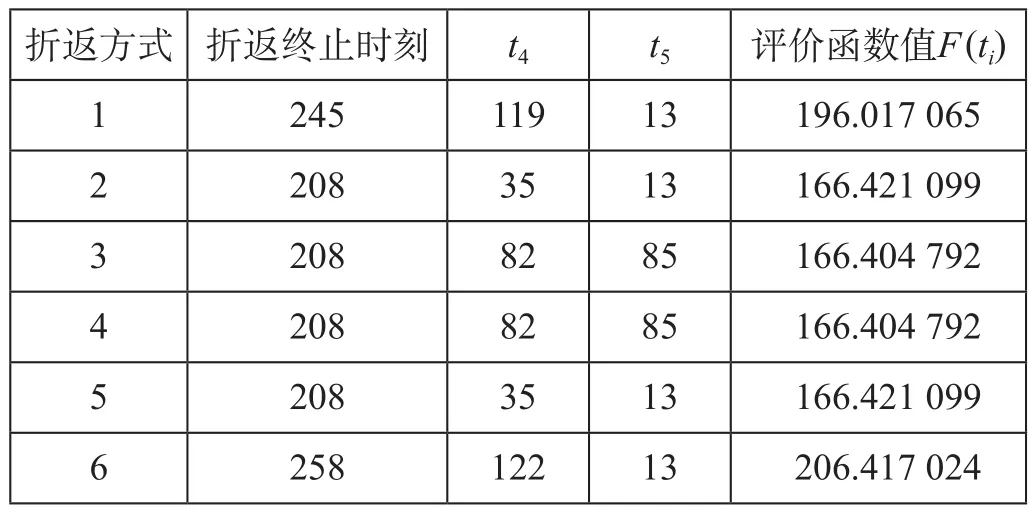
表 1 寻优计算结果统计表Tab.1 The statistics results of optimization

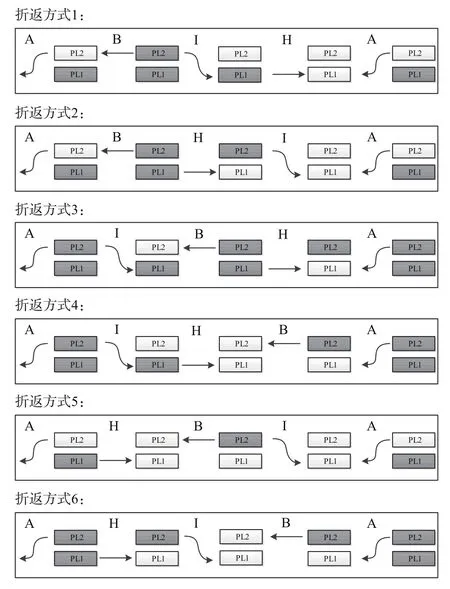
图 6 站台有车示意图Fig.6 The diagram to indicate when there is train on the platform

式中：Fplt(tj) 为站台有车情况的统计结果，列车在终端站停站时间越长，统计结果Fplt(tj) 越小。

折返方式的横向比选阶段，以每种折返方式的最终适应度评价值和其站台有车情况的光栅统计结果之和作为折返方式的横向比选函数，可以表示为

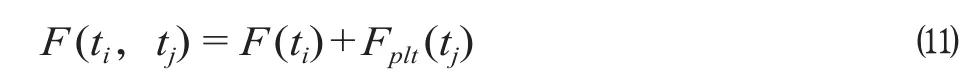
式中：F(ti) 为折返分析时适应度评价函数。

经计算得出折返方式 3 (A-I-B-H-A) 的横向比选值最小，因而折返方式 3 为最优折返方式。折返方式 3 下所得的站前平均折返间隔Ttb为 89 s，基于该折返方式和其到发车时间，在天津轨道交通 9 号线现场编制时刻表进行验证，真车实测结果为 91 s，与仿真结果基本一致。

4 结束语

通过对城市轨道交通终端站的列车折返过程划分阶段，将实际应用中的过程参数和折返评判标准与粒子群遗传算法的向量和适应度评价函数进行映射，并依此编制寻优计算软件，完成列车终端站最优折返方式的计算机自动选择，现场实测最优折返方式下的折返时间，探索出一条通过计算机对终端站的折返方式自动智能寻优的可行之路。基于粒子群遗传算法的折返方式寻优软件计算出的最优折返方式，以及该方式下的各站到发车时间，为优化运营时刻表、缩短运营间隔、提高运营效率提供了指导和数据支撑。下一步将研究如何实现算法与全线的运行过程结合，综合出入段、大小交路套跑等运营场景，自动输出最优的运营间隔和时刻表，使得基于粒子群遗传算法的时刻表优化软件更具实用性。

参考文献：

[1]王俊锋，孙 旺，郜洪民. 城市轨道交通车站站前折返间隔分析[J]. 城市轨道交通研究，2013，16(4)：69-73.WANG Jun-feng，SUN Wang，GAO Hong-min. Analysis of Pre-station Turn-back Headway in Urban Rail Transit[J].Urban Mass Transit，2013，16(4)：69-73.

[2]王燕燕，葛洪伟，王娟娟，等. 一种动态分组的粒子群优化算法[J]. 计算机工程，2015，41(1)：180-185.WANG Yan-yan，GE Hong-wei，WANG Juan-juan，et al.A Particle Swarm Optimization Algorithm of Dynamic Grouping[J]. Computer Engineering，2015，41(1)：180-185.

[3]李 霞. 粒子群遗传优化算法[J]. 电脑知识与技术，2008，4(S2)：171-172.

[4]童佳楠，聂 磊，贺振欢. 基于遗传算法的动车运用所一级检修作业计划优化[J]. 铁道运输与经济， 2016，38(8)：59-65.TONG Jia-nan，NIE Lei，HE Zhen-huan. Optimization of First-Level Maintenance Plan in EMU Depot based on Genetic Algorithm[J]. Railway Transport and Economy，2016，38(8)：59-65.

[5]REEVES C R. A Genetic Algorithm for Flowshop Sequencing[J]. Computers & Operations Research，1995，22(1)：5-13.

[6]徐小亮，柴慧君，薛 强. 地铁列车站前折返效率影响因素分析[J]. 城市轨道交通研究，2014，17(10)：119-121.XU Xiao-liang，CHAI Hui-jun，XUE Qiang. Analysis of Factors Influencing the Front Turnback Efficiency of Metro Train[J]. Urban Mass Transit，2014，17(10)：119-121.

[7]苗 沁，周天星. 城市轨道交通折返站折返能力分析[J].城市轨道交通研究，2010，13(11)：57-61.MIAO Qin，ZHOU Tian-xing. Analysis of Turning-back Capacity at Urban Rail Transit Station[J]. Urban Mass Transit，2010，13(11)：57-61.

[8]王道敏. ATO 站台精确停车功能实现的制约因素分析[J].铁路通信信号工程技术，2012，9(4)：41-43.

[9]卢星儒，杨菊花，温永瑞. 基于最优组合赋权的货运方式选择可变模糊模型研究[J]. 铁道货运，2017，35(1)：16-22.LU Xing-ru，YANG Ju-hua，WEN Yong-rui. Study on Variable Fuzzy Model of Freight Transport Modes Selection based on Optimal Combination Weight[J]. Railway Freight Transport，2017，35(1)：16-22.

[10]刘丽珏，蔡自兴. 基于克隆选择的粒子群优化算法[J]. 小型微型计算机系统，2006，27(9)：1708-1710.LIU Li-jue，CAI Zi-xing. Particle Swarm Optimization Algorithms based on Clonal[J]. Mini-Micro Systems，2006，27(9)：1708-1710.