基于 X-12-ARIMA 模型的公路运价季节性波动影响研究
张梦迪,黄玮青,安姝静
ZHANG Meng-di1,HUANG Wei-qing2,AN Shu-jing3
(1.中国铁道科学研究院 研究生部,北京 100081;2.中国铁路总公司 货运部,北京 100844; 3.中国铁路总公司 发展和改革部,北京 100844)
(1.Postgraduate Department, China Academy of Railway Sciences, Beijing 100081, China; 2.Freight Transport Department, China Railway Corporation, Beijing 100844, China; 3.Development and Reform Department, China Railway Corporation, Beijing 100844, China)
0 引言
随着当前我国市场化改革的稳步推进,铁路货运价格正逐步由政府指导价过渡到运输企业自主定价。根据国家发展和改革委员会 [2017]2163 号文件,自 2018 年 1 月起铁路集装箱、零担各类货物运输价格,以及整车运输的 12 个货物品类的运输价格开始实行市场调节,由铁路运输企业自主制定;其他实行政府指导价的整车运输各货物品类可以参照基准运价在上浮不超过 15% 的范围内由铁路企业自主确定运价水平。在市场经济中,分析竞争对手的产品价格是企业制定和调整价格的重要步骤之一,铁路运输企业在制定和实施系列应对市场变化的价格策略时,也应充分考虑公路货运价格的因素。因此,分析研究公路运输价格的波动情况对提高铁路运输企业的市场竞争应对能力、完善企业价格决策具有现实意义。
在我国学者已经开展的关于运输领域季节性波动研究中,马银波[1]对中国公路货运运价和运输量时间序列进行实证分析,提出季节性因素是造成公路货运价格短期波动的主要原因;桂文林等[2]运用指数平滑模型对铁路客、货运量的季节波动特征进行分析,认为铁路客、货运量均具有显著的季节特征;孙嘉欣[3]运用 X-12-ARIMA 模型对铁路大宗货物的运输需求进行季节性分析,提出浮动运价可以提高运输企业经营质量,并据此对货运低谷季、高峰季的最优浮动运价进行建模估计。考虑到近年来我国铁路货运形势的发展,以及运输市场格局的变化,需要从支撑铁路货运价格决策的角度开展对公路货运价格的季节性波动研究。为此,选取 X-12-ARIMA 方法研究公路运价的季节性波动情况,并结合案例分析进行量化研究,为铁路运输企业运价制定提供参考。
1 X-12-ARIMA 模型
时间序列是按照时间顺序记录的一组有序数据,季节性因素是指使时间序列呈现出和季节变化相关的、稳定的周期波动因素。X-12-ARIMA 模型是进行时间序列因素分解时较为常用的标准方法[4],它能有效计算和提取时间序列中的季节性因素并测度该因素对序列波动的影响程度。运用到价格时间序列上,可以分析和掌握季节性因素对价格波动的影响,对于行业价格水平及其浮动程度的把握具有重要的参考价值。X-12-ARIMA 模型是在移动平均方法的基础上引进“随机建模思想”发展而来,采用该模型完成季节性因素的提取步骤如下。
(1)步骤 1:通过建立回归方程检测月度 (或季度) 长度、工作日、交易日、闰年等因素对时间序列的影响是否显著。具体做法是,根据时间序列特点有选择地考察序列是否会受以上因素的影响,将待考察因素作为自变量,将原始时间序列 (原始时间序列用Yt表示,其中t表示该时间序列有n个观察值t= 1,2,…,n,下同) 进行对数处理后的时间序列yt= InYt作为因变量构造回归方程 (对数处理不会改变时间序列数据的性质和相关关系,但可以缩小数据的绝对数值,方便计算)。对回归方程的参数进行显著性检验,如果 P值小于显著水平则说明对应因素是时间序列yt的显著影响因素,此时可以对该因素进行提取,并将其记为xit(i= 1,2,…,r);反之,则说明该因素不是时间序列yt的显著影响因素,在下一步拟合求和自回归移动平均模型 (Autoregressive Integrated Moving Average,ARIMA) 时可以不考虑该因素[5]。按照这种方法,依次验证、提取时间序列的影响因素。
(2)步骤 2:视上一步各因素的参数是否显著,对以上回归的残差序列或时间序列yt进行ARIMA 模型的拟合,以实现对原时间序列向前和向后的数据扩充,保证在下一步使用移动平均方法时不会出现前k期和最后k期数据拟合值缺失的情况[6]。ARIMA 模型是指将非平稳时间序列转化为平稳时间序列,然后将因变量仅对其滞后值、随机误差项的现值和滞后值进行回归所建立的模型。根据博克斯-詹金斯 (Box-Jenkins) 的建模思想,构建ARIMA 模型主要考虑以下过程[7]。
①确定非季节性、季节性平稳差分阶数。使用ADF (Augmented Dickey-Fuller) 检验法检查时间序列yt的平稳性,如果 ADF 检验值在一定的置信水平下大于临界值,则认为时间序列非平稳;反之则认为时间序列平稳。对非平稳时间序列yt进行差分变换可使其平稳,以达到建立 ARIMA 模型的条件。使时间序列平稳而差分的阶数即为非季节性和季节性差分阶数d,D。
②确定季节性、非季节性滞后阶数。通过偏相关系数、自相关系数等统计量的季节性、非季节性滞后特征,确定非季节性自回归的阶数p、非季节性移动平均的阶数q、季节性自回归的阶数P、季节性移动平均的阶数Q。
③进行 ARIMA 模型拟合,模型形式为

式中:非季节性p阶自回归系数多项式的展开形式为,其中ϕ1,ϕ2,…,ϕp为自回归模型系数;非季节性q阶移动平均系数多项式的展开形式为其中θ1,θ2,…,θq为移动平均模型系数;季节性p阶自回归系数多项式ΦP(Ls) 展开形式为,其中Φ1,Φ2,…,ΦP为自回归模型系数;季节性Q阶移动平均系数多项式 ΘQ(Ls) 展开形式为其中 Θ1,Θ2,…,ΘQ为移动平均模型系数;季节差分是指 (1-Ls) =yt-yt-s;D阶季节差分为 (1-Ls)Dyt;L为延迟算子,表示把当前序列值的时间向前推迟一期,即L·yt=yt-1;s为周期长度,选取月度数据时s= 12;xit为确定的显著影响因素 (i= 1,2,…,r);βi为第i个参数,i为回归方差显著因素的项数;误差项εt的均值为 0,方差为δ2。
如果回归方程中所考虑的月度 (或季度) 长度、工作日、交易日、闰年等所有因素均不显著,则不需要添加项,此时按照以下形式直接对yt进行 ARIMA 模型的拟合。

④模型计算与诊断。在确定模型表达式的基础上计算模型中的未知参数,并通过整体统计量Q对建模结果进行诊断、评价。统计量Q小于门限值 1时,认为所拟合的 ARIMA 模型与原时间序列的数据特征相符,可以在此基础上对季节性因素做进一步的提取。
(3)步骤 3:在建立模型并进行数据扩充的基础上,基于简单中心移动平均、Henderson 加权移动平均、Musgrave 非对称移动平均 3 类移动平均方法经过多次重复迭代计算,实现对时间序列yt中季节性因素的提取,最终得到季节性因素分解结果。提取所得的季节性因素对时间序列yt的影响程度可以用季节性因素变化百分比的方差相对贡献度来描述,方差相对贡献度所占百分比越大,则表示其对时间序列yt的影响程度越强。
2 实例分析
以北京至上海 13 m 整车、零担轻货的公路运价时间序列为例,通过构建 X-12-ARIMA 模型,研究运价时间序列的季节性波动情况。根据中国物流与采购联合会公布的物流节点城市间每周平均采样公路运价,选取 2013 年 1 月—2017 年 7 月北京至上海公路 13 m 整车、零担轻货的运价,取对应周数据的简单平均计算每月价格。北京至上海 13 m整车运价序列用yt表示、零担轻货运价序列用zt表示。对数处理后的运价序列如表 1 所示。
首先,对时间序列的显著影响因素进行考察。研究所采用的每月数据为对应每周运价的简单平均,故不存在交易日因素。根据时间序列yt,zt的特点,选择月度长度、工作日、闰年因素作为自变量,分别构造时间序列yt,zt的回归方程。显著性检验结果显示,各回归方程参数的 P 值均远大于0.05 的显著性水平,说明以上 3 个因素均不是时间序列yt,zt的显著影响因素。
其次,依照博克斯-詹金斯的建模思想,按照确定平稳差分阶数、确定季节性和非季节性滞后阶数、ARIMA 模型拟合、计算与诊断的步骤,分别对时间序列yt和zt构建 ARIMA 模型,北京至上海 13 m 整车、零担轻货运价 ARIMA 模型构建如表 2 所示。
第三,运用简单中心移动平均、Henderson 加权移动平均、Musgrave 非对称移动平均 3 类移动平均方法计算、分解得到 2 个时间序列的季节性因素。季节性分解结果表明,yt和zt均具有显著的季节性特征。具体表现为:①13 m 整车运价的季节性因素随时间的推移呈现有规律的波动,各年度同月价格水平基本保持不变,季节性因素对其影响相对稳定。季节性特征为,天气转暖促使货物运输需求步入旺季,表现为 4 月运价达到年度高点,此时季节性因素影响程度最高;高温、雨季导致货物运输需求减弱,8 月运价达到年度低值。②零担轻货运价的季节性因素随着时间的推移波动幅度逐渐增大,季节性因素对其影响程度逐渐增强。季节性特征为,受网络电商年中促销、节假日前民生消费需求活跃、岁末用工供给不足等原因综合影响,1 月、6 月运价达到年度高点;由于春节前后企业生产经营活动放缓、夏季高温多雨等原因影响,2 月、8 月运价为年度低点。
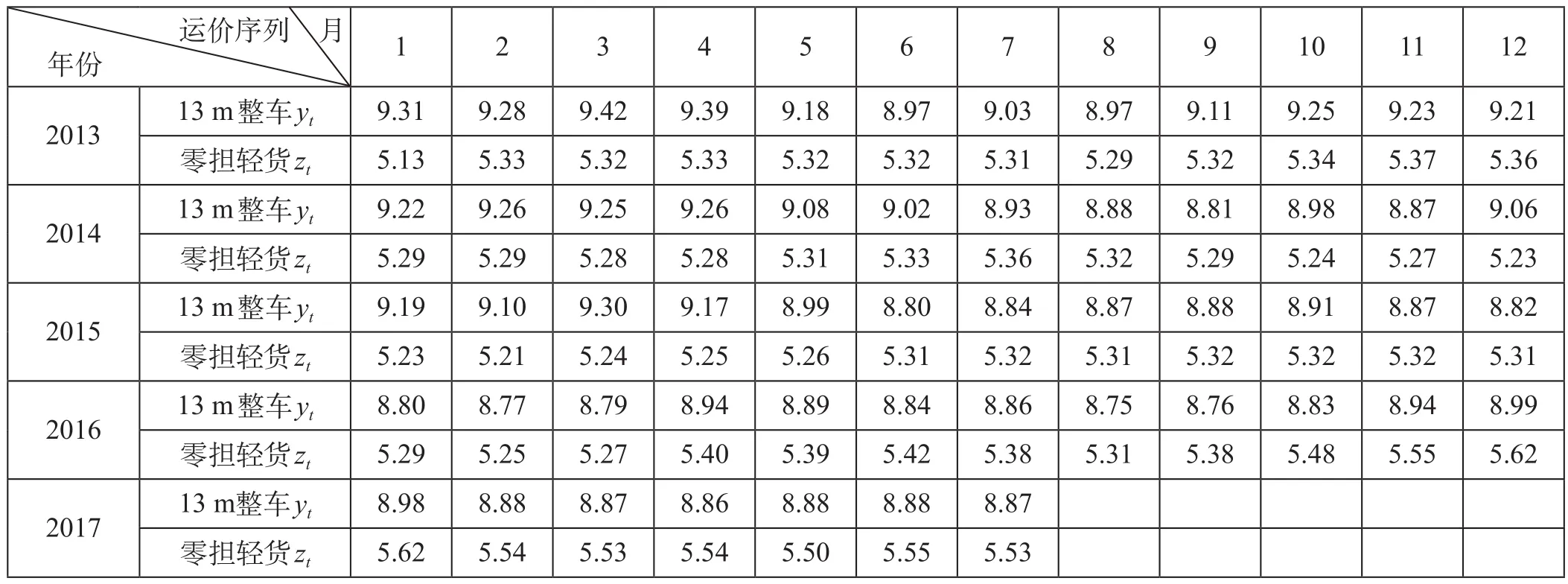
表 1 对数处理后的运价序列Tab.1 Time series of freight price after natural logarithm processing
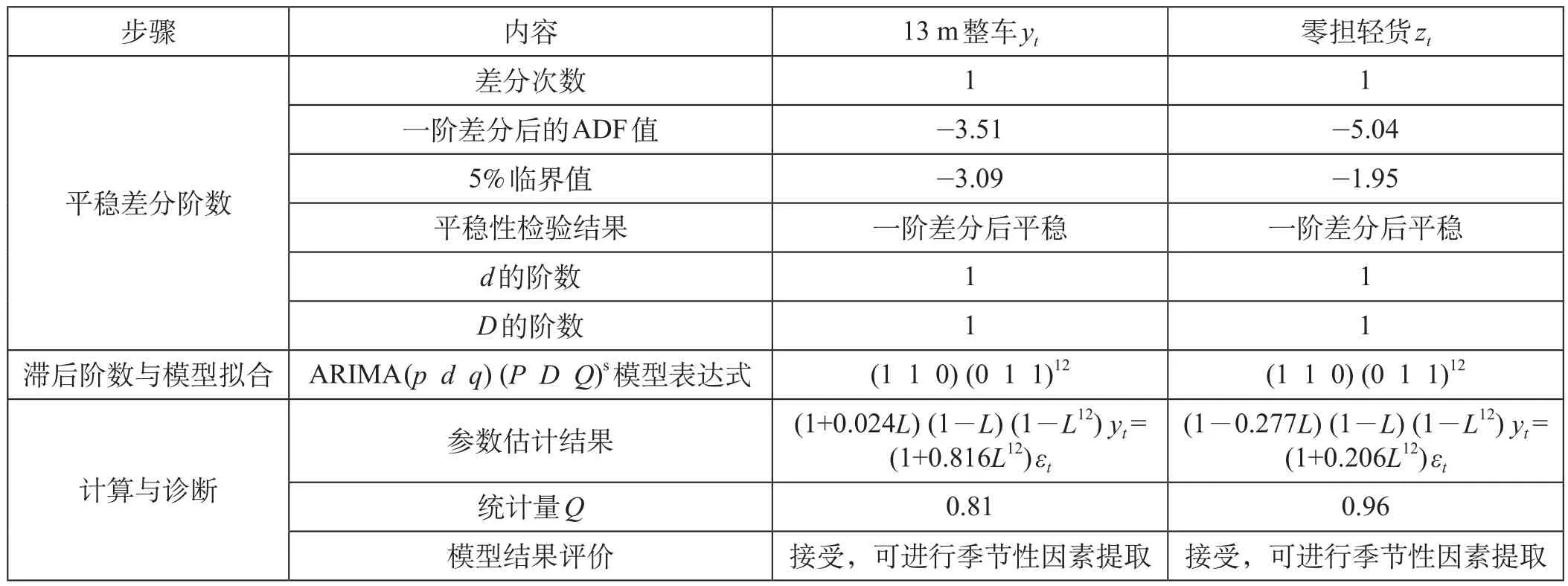
表 2 ARIMA 模型构建Tab.2 The construction of ARIMA models
第四,从方差相对贡献度分析季节性因素影响程度,季节性因素变化百分比的方差相对贡献度如表 3 所示。①对于 13 m 整车,其短期内 (2 个月)的运价波动主要受季节性因素的影响,上月季节性因素对本月的运价变化影响较强,贡献度占比超过50%;综合 12 个月的情况来看,季节性因素对运价变化的影响作用随着时间推移逐渐衰减,其第1月的季节性因素对第 2 月价格变化的影响程度占比为54.21%,而对次年同月运价变化的影响程度仅占0.18%。②对于零担轻货,其短期内 (2 个月) 的运价波动主要受季节性因素影响,上月季节性因素对本月的运价变化影响较强,贡献度占比超过 50%;综合 12 个月的情况来看,季节性因素对运价变化的影响作用在波动中逐渐降低。以上分析说明,在短期内 (2 个月) 季节性因素对京沪 13 m 整车、零担轻货运价的影响程度较强。因此,在进行公路运输价格分析时应充分考虑季节性因素。

表 3 季节性因素变化百分比的方差相对贡献度Tab.3 Relative contributions to the variance of the percentage change of seasonal factor
3 结束语
在我国铁路货运价格逐步放松管制的过程中,开展公路运价波动研究、掌握公路运价变化规律对于铁路运输企业具有现实意义。铁路运输企业应充分利用国家赋予的运价权限,逐步建立价格动态调整机制,通过参考公路运输各车型重点线路的历史价格及其季节性、区域性波动规律和幅度,根据铁路货物品类、车型、区域、季节等不同的市场状况对货运市场进行细分,适度增加运价灵活性,采取差异化的价格策略实现对铁路运价的精细化管理。同时,应发挥好价格调节资源配置的基础性作用,如在公路运价显著上升的季节或区域适当上调铁路货运价格;在公路运价持续下降的季节或区域适当有针对性地下调铁路货运价格[8]。此外,铁路运输企业还可以在综合参考公路货运年度价格均值的基础上,在保证盈利的前提下,针对铁路运输重点客户提供具有竞争力的协议价,促进铁路运输企业的持续健康发展。
参考文献:
[1]马银波. 公路货运价格与需求动态关系的实证分析[J]. 长安大学学报 (社会科学版),2008(3):7-12.MA Yin-bo. Empirical Analysis on the Relationship between the Price and Demand of the Trucking Industry in China[J].Journal of Chang’an University(Social Science Edition),2008(3):7-12.
[2]桂文林,潘庆年. 我国铁路运量波动的季节因素分析[J].铁道运输与经济,2010,32(6):79-82.GUI Wen-lin,PAN Qing-nian. Analysis on Seasonal Factors of Railway Traffic Volume Fluctuation in China[J]. Railway Transport and Economy,2010,32(6):79-82.
[3]孙嘉欣. 铁路大宗货物运价浮动研究[D]. 成都:西南交通大学,2017.SUN Jia-xin. Research on Rail Commodities Freight Rate Floating[D]. Chengdu:Southwest Jiaotong University,2017.
[4]高铁梅. 计量经济分析方法与建模[M]. 北京:清华大学出版社,2016.
[5]朱加发,王怀相. 基于格兰杰因果关系检验的铁路与城市化关系研究[J]. 铁道运输与经济,2017,39(4):64-68.ZHU Jia-fa,WANG Huai-xiang. Study on the Relationship between Railway and Urbanization based on Granger Causality Test[J]. Railway Transport and Economy,2017,39(4):64-68.
[6]潘泽清. 时间序列季节调整的必要性、方法以及春节效应的调整[J]. 财政研究,2013(5):29-33.
[7]BOX G E P,JENKINS G M,REINSEL G C. Time Series Analysis:Forcasting and Control( Fifth Edition)[M].Hoboken:Wiley,2015.
[8]宋小满. 公路货运价格监测实践与启示[J]. 铁道货运,2017,35(9):39-42.SONG Xiao-man. Practice and Revelation of Highway Freight Price Monitoring[J]. Railway Freight Transport,2017,35(9):39-42.

