基于改进果蝇算法的重载运输车流组织优化研究

景龙刚，李国宁

JING Long-gang, LI Guo-ning

（兰州交通大学 自动化与电气工程学院，甘肃 兰州 730000)

(School of Automation and Electrical Engineering， Lanzhou Jiaotong University， Lanzhou 730000，Gansu， China)

0 引言

重载运输以其大运量、低成本的优势已经成为我国铁路运输的主要组织形式，同时世界范围内重载运输发展趋势充分体现出提高轴重、增加列车编组数量的列车组织形式更加科学、高效。随着我国煤炭、矿石等资源需求量的快速增加，越来越多的干线铁路在进行扩能改造后并入重载线路，这将极大促进重载运输的飞速发展，并对优化车流组织提出更高的要求。我国重载列车因装车地条件的差异存在单元式、整列式、组合式等多种类型列车，其装车区一般分布在矿产资源密集的能源产地或数条铁路线路的交叉枢纽上，由这些密集的装车点构成的战略装车域为重载铁路提供稳定的货源供给[1-2]。同时，既有线运输能力提升后并入重载线路枢纽站和新建重载铁路，使铁路运输在路径选择上的灵活性极大增强，这些因素统一构成了现代化的重载运输网。

国内学者对重载运输车流优化进行了很有价值的研究。王慈光[3]以重载铁路扩充运量为背景，创新性提出目标规划技术，并成功应用到重载列车开行方案的组织规划中，确定了列车开行方案和机车使用数量的消耗，但模型对于具体的装车点配流方案没有做出详细分析。赵鹏[4]根据重载铁路网与网络图的特点，构建重载列车组合运输网络拓扑图，以组合时间最小、通过能力最大为目标，引入组合系数概念解决列车组合数量分配不均衡等问题，但因现场实际组合情况的不确定性，既有研究引用组合系数概念的合理性还有待进一步验证。韩雪松等[5]根据装车区车流组织特征，在考虑各种应用约束的情况下，建立最小列车组合时间的目标函数，在约束条件中定义组合映射关系来解决组合问题，设计了启发式算法求解，但在组合映射关系中未能考虑实际运输情况。

因此，在上述研究基础上创新性提出多路径的重载路网模型。该模型相比于专线运输模式更符合我国铁路运输组织情形，同时还需要考虑在重载线路上进行组合、分解作业时发生换重的情况。当支线运输并入主干线路时进行组合作业提高牵引质量，减少编组数量；当主干线路需要分流于支线铁路时进行分解作业，减少单车牵引质量，降低线路设备损耗。综上所述，建立基于多路径选择和运输通道部分枢纽站点换重的车流组织优化模型。

1 重载运输车流组织模型构建

根据我国重载铁路列车以整列式为主，兼顾组合列车、单元列车特点及考虑扩能为主的目的，可以将存在路径选择和站点换重作业的重载运输车流组织优化问题定义为：由战略装车地出发的重载列车，经过适当的组合改编及择优的路径运往卸车地。但是，由于运输通道的能力限制及尽量减少中途作业量的考虑，重载列车以组合为大编组的技术直达列车和点对点的直达列车为主要运输方式，在现有资源下发挥最大的铁路运能。

1.1 模型定义

现引入以下集合及参数：V为运输路网中的所有技术站或组合站；V(s) 为与装车地相邻的技术站；Q(s) 为与卸车地相邻的技术站集合；Cs为重载车流在装车地集结消耗的时间参数；Ust为重载列车卸车地每车作业时间消耗；Nst为无任何中转或改编作业的重载直达列车的日均计划车流量；Kst为从装车地s经过初始技术站进行组合后开至卸车地的技术直达列车日均计划车流量；Pst为从装车地开至卸车地途中存在改编作业的非直达列车的日均计划量；Vst为非直达车流在卸车地每车所额外消耗的作业时间；τ0为在装车地技术站k0组合作业的平均时间；τ为经过途中技术站进行改编作业较直达列车每车所增加的作业时间为直达车流组织经过路径l从装车站s开往卸车站t的在途旅行时间；Tab技术直达车流在途中a站到b站所花费的旅行时间；解体车流 (小编组车流) 在途中a站到b站所花费的旅行时间。

1.2 约束条件

（1）运量约束。模型首先需要满足年度目标运量的要求，其约束表示为

式中：λ1，λ2，λ3分别代表直达车流、技术直达车流、非直达车流的满载率；η1，η2，η3分别代表直达车流、技术直达车流、非直达车流的平均载重系数；G为重载线路年度计划运量；Θb为货物流量月均波动系数。

（2）装卸车约束条件。重载运输的货物作业量需要满足装车区和卸车区作业的最大能力限制，其约束可以表示为

（3）重载主干线路能力约束可以表示为

式中：Q为重载主干线的最大通过能力。

（4）路径l的通过能力限制可以表示为

（5）技术站的能力限制可以表示为

（6）铁路径路网络主干线与支线车流量之间关系可以表示为

式中：h为路网中的路径数量。

1.3 目标函数

重载运输车流组织的优化目标是使所有车流在约束条件下以最小的总换算车小时运行。

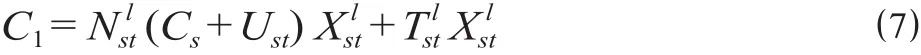
综上，重载铁路网上的总时间消耗为

2 基于改进果蝇算法的重载运输车流组织优化模型求解

在重载车流组织模型中，针对车流特性所定义的整形变量会随着重载铁路网复杂度及车流去向的增多而增加，使问题求解变得困难。果蝇优化算法( Fruit Fly Optimization Algorithm，FOA) 是模仿果蝇觅食的生物行为而推演出寻求全局优化解的新方法，该算法相对于经典的遗传算法 (GA)、蚁群算法 (ACO)、粒子群算法 (PSO) 等群智能搜索算法在收敛速度、寻优效率方面具有更好的优势。根据车流模型中设置的众多 0-1 变量的特点及换重作业后代表车流性质的 0-1 变量改变，可以猜测技术站直达车流与非直达车流的计算量较大。为使果蝇算法得到满足约束条件的优化解，需要对果蝇算法进行一定改进[6-7]。

2.1 果蝇算法及改进

果蝇优化算法固定搜索步长h，导致其不能充分利用目标函数所提供的群体信息。同时，算法对比寻找最优果蝇个体的进化趋势，存在过早收敛于局部解的问题[8]。因此，如何制定步长h的调整策略和设计逃逸机制，是成功改进算法的关键。由此，研究提出了基于高斯变异的自适应果蝇优化算法，通过计算平均适应度值的变化率和取最值函数的方法来平滑调节步长。对抑制早熟收敛问题，在判断算法早熟收敛后加入扰动策略，高斯变异的自适应果蝇优化算法如图 1 所示。

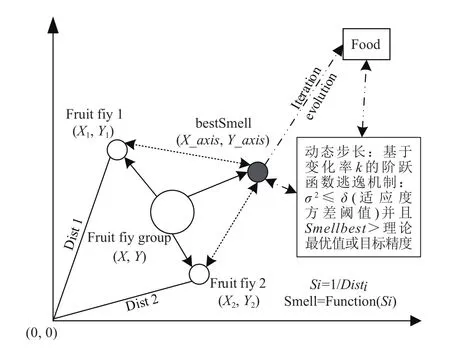
图 1 高斯变异的自适应果蝇优化算法Fig.1 Adaptive improved fruit fly algorithm base on gauss mutation

2.1.1 适应性动态步长调整策略

在基本 FOA 中，果蝇迭代进化没有挖掘味道浓度之后的种群适应度函数信息，使算法搜索方向不确定，启发性不高[9]。因此，改进的动态步长需要充分利用种群反馈的适应度值变化信息。

定义 1：根据味道判定值计算果蝇群体的平均适应度值Aj为

式中：N为种群规模；fi(j) 为第j代中果蝇i的适应度函数值。

定义 2：基于种群反馈信息的适应值变化率k定义为

当变化率k较大时，表明搜索空间变化率相对步长较大，说明可以增加步长提高解空间搜索能力，增加搜索开发率。当k较小时，表明搜索空间相对平滑和单调，此时采取减小步长的搜索策略，一是提高找到优化解的可能性，二是增加果蝇种群对解空间的搜索深度。因此，步长调整公式如下。

式中：ht为种群第t代搜索步长；α和β为步长变化幅度调节参数。

由于在不同代之间迭代时k值变化较大，使搜索过程极不稳定，因而在增加步长时选择自然对数，减小步长时选择 e 指数函数，可以显著降低步长变化幅度，改善ht+1的平滑性。

2.1.2 局部逃逸判断机制

基本 FOA 算法易陷入局部解且很难逃逸出局部最优解，降低了算法收敛准确性和收敛精度。由此，在果蝇算法每执行 1 次迭代后，判断是否发生早熟收敛问题。如果是，则执行高斯变异扰动。

逃逸原理：如果σ2≤δ(适应度方差阈值) 并且Smellbest＞理论最优值或目标精度 (这里考虑的是最小化情况)，则判定算法陷入了局部最优。此时，随机选择M个最优果蝇个体复制并按照概率P对其位置执行高斯变异扰动，得到新的位置继续重复迭代工作。

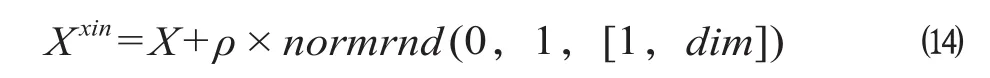
式中：X为扰动前果蝇位置；X xin为执行扰动后位置；ρ为扰动幅度调节参数；normrnd为服从正态分布的随机数矩阵；dim为矩阵维数。

2.2 改进果蝇算法流程

（1）初始化种群参数：果蝇个体位置，种群规模Sizepop，迭代次数Maxgen，味道浓度 (适应度方差) 阈值δ，果蝇个体复制数M，高斯变异概率P。

（2）根据果蝇种群平均适应度值变化率k，更新迭代步长，计算新的果蝇个体位置。

（3）根据基本果蝇算法步骤，找到最佳味道浓度果蝇个体并记录其位置。

（4）分别计算果蝇种群的Smellavg(平均味道浓度)和果蝇群体σ2(适应度方差)。

（5）判断果蝇进化是否陷入了局部最优。如果是，复制M个最优果蝇个体，重新初始化迭代步长。

（6）利用均匀分布函数获得随机数C∈ [0，1]。如果C≤P，按照公式 ⒁ 对复制的果蝇个体执行高斯扰动操作，实现位置更新。

（7）判断迭代结束标志。①当前种群迭代适应度值等于理论适应度值或目标精度。②迭代次数达到设定Maxgen。如果条件满足，则输出最优解及对应果蝇个体位置；否则，转向步骤（2），循环执行迭代操作。

3 算例分析

为验证模型与算法的合理有效，选择神朔铁路(神木县—朔州) 干线中 2 个枢纽车站巴图塔站与神池南站，在考虑巴准线 (巴图塔—准格尔旗)、准池线(外西沟—神池南) 并入神池南站后急剧扩充运量的情况下，简化路网模型后设计一个多路径的重载铁路运输网络算例，多路径的路网模型如图 2 所示。其中，0 表示与装车地相邻的技术站，10 表示与卸车地相邻的解体技术站。

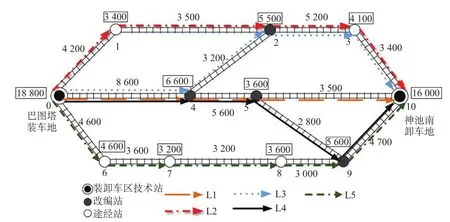
图 2 多路径的路网模型Fig.2 Multi-path road network model

在该铁路网中，运营管理部门计划下一年途经巴图塔站至神池南站的运量为 3.68 亿 t，运输车辆采用 C80的车型，其列车平均载重系数为 0.96，满载率为 0.98[10]。直达列车采用大编组方式时列车编成辆数为 132 辆，小编组方式时为 66 辆。

针对重载运输优化最小消耗的特点，采用改进果蝇算法对 ⑽ 式的目标函数在约束条件下的消耗进行优化求解，改进果蝇算法的参数设置如下。种群数量Sizepop= 60，最大迭代次数Maxgen= 200，初始搜索步长h= 1×104，适应度方差阈值δ= 1e-3；初始化果蝇群体位置区间为 [6.0×105，7.0×105]。步长幅度调节参数α= 0.9、β= 0.2，变异概率P= 0.35。

在计算机仿真中采用改进果蝇算法求解约束模型，改进果蝇算法优化车流模型的仿真曲线如图 3所示。

从仿真曲线中可以看出，与果蝇算法相比，改进果蝇算法在收敛速度、寻优精度方面都有了很好的改善。多次试验还发现改进果蝇算法迭代稳定，基本不会发生陷入局部解的情况。通过设置变异个数M的不同对比发现，M值的选择不宜过大，否则会导致迭代后期收敛速度降低，原因在于M值越大，就会扩大解的搜索范围，这在进化前期是比较有利的，增强搜索的广度，但在搜索后期影响算法执行速度与效率。因此，在此选择M= 5 时寻得最优值。

最后通过分析整理，构造的优化路网方案集合如表 1 所示。

仿真计算并分析结果得出，当改进果蝇算法迭代次数为 84 时，模型得到最优解，其总的最小消耗换算车小时为632 780。同时，从图 3 可以看出，迭代第50 次时，基本能得到一个较为满意的优化解，基本符合实际现场的运营情况。但是，如果迭代继续进行，算法还能够找到更优化的解，进一步说明改进果蝇算法的计算精度高，寻优能力强。优化运输方案如图 4 所示。

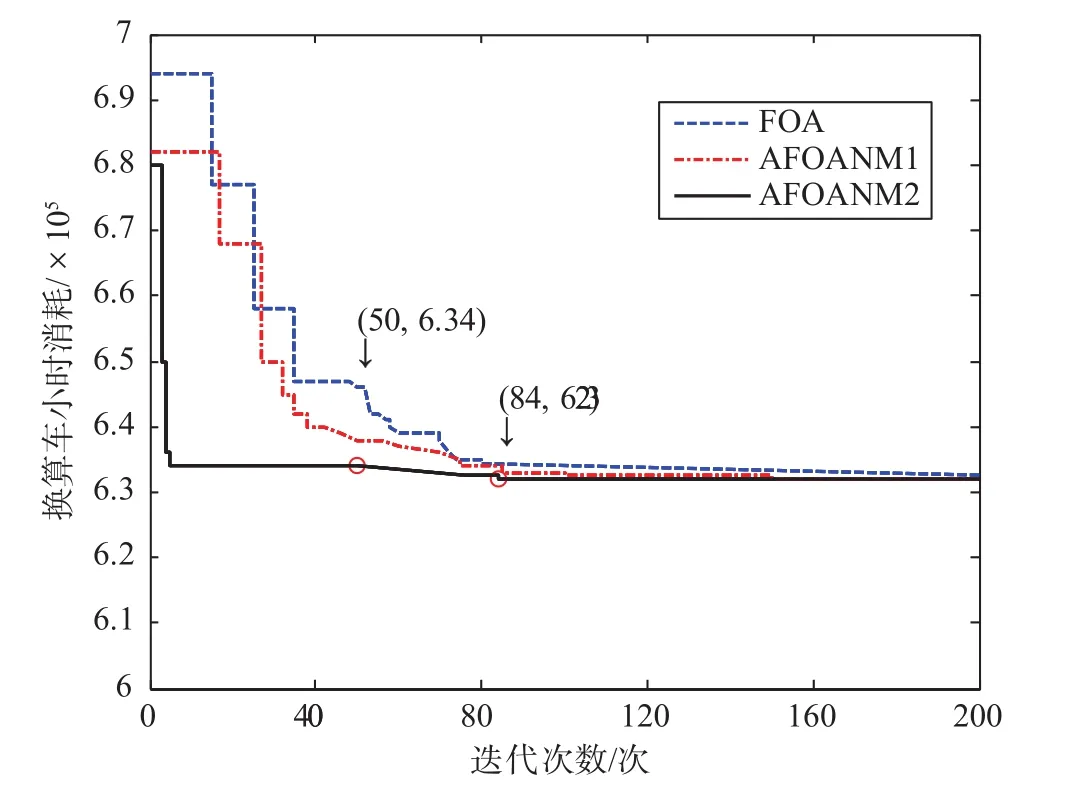
图 3 改进果蝇算法优化车流模型的仿真曲线Fig.3 Simulation curve of improved fruit fly algorithm optimization of vehicle flow model

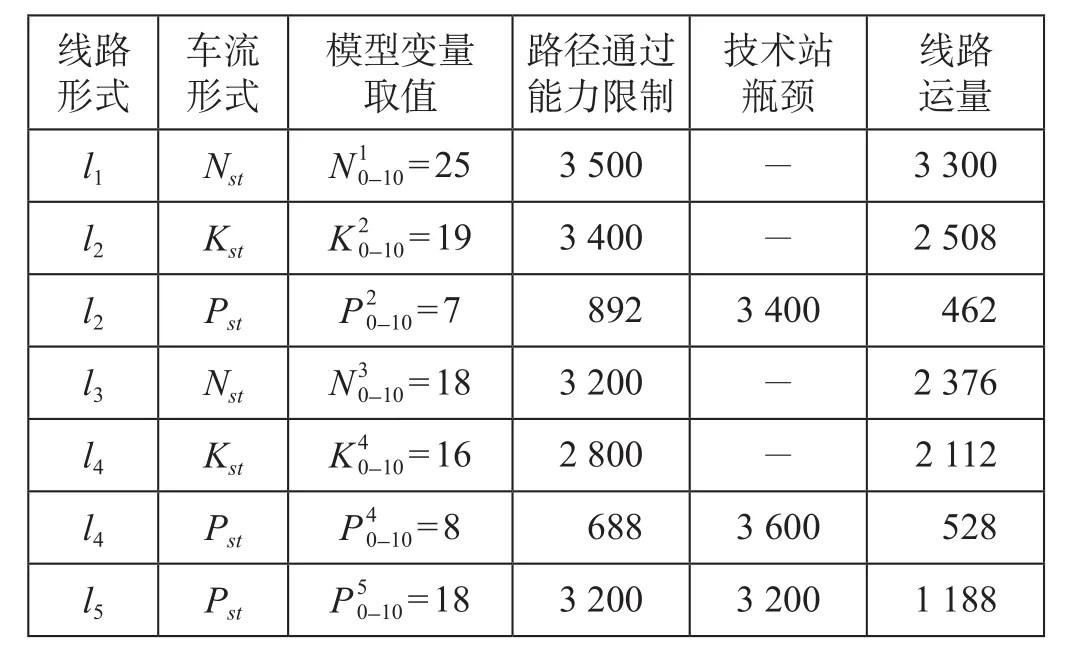
表 1 优化路网方案集合Tab.1 Optimization road network plan collection

图 4 优化运输方案Fig.4 Optimization transportation scheme of example model

4 结束语

优化重载运输组织策略是重载运输管理向着智能化、高效化发展的重要部分，也是重载铁路运输提高效益、增强竞争力、节约成本的重要措施。在考虑重载路网存在路径选择、部分站点换重的特殊情况下分析约束条件，建立重载运输车流组织模型。针对模型中车流组织特性及路网复杂性，运用改进果蝇算法求解大规模非线性规划问题，计算结果精确、合理，可以为铁路行车组织方案的优化提供指导。此外，通过把群智能搜索算法应用于车流计算与规划中，不仅是对铁路运输组织理论的补充与完善，而且推动了铁路信息智能计算的发展，为解决重载运输车流组织实际问题提供理论依据。

参考文献：

[1]范振平，乐逸祥. 基于蚁群算法的装车地直达重载运输优化模型求解算法研究[J]. 物流技术，2007，26(8)：110-114.

[2]刘 俊. 优化铁路运输调度指挥体系策略的研究[J]. 铁道运输与经济，2017，39 (5)：1-6.LIU Jun. Study on Strategies of Optimizing Railway Traffc Control Command System[J]. Railway Transport and Economy，2017，39(5)：1-6.

[3]王慈光. 目标规划在铁路重载运输组织中的应用[J]. 西南交通大学学报，2009，44(3)：113-117.

[4]赵 鹏. 基于组合列车的重载铁路装车区车流组织优化模型研究[J]. 中国铁道科学，2010，31(6)：116-121.ZHAO Peng. Study on the Optimization Model of Car Flower Organization in the Loading Area of Heavy Haul Railway based on the Combined Trains[J]. China Railway Science，2010，31(6)：116-121.

[5]韩雪松，赵 军，彭其渊. 多组合站条件下重载运输战略装车域列流组合方案优化[J]. 铁道学报，2012(8)：1-6.HAN Xue-song，ZHAO Jun，PENG Qi-yuan. Optimization of Train Flow Combination Scheme for Strategic Heavy Haul Loading Domain at Multi-combination Stations[J]. Journal of the China Railway Society，2012(8)：1-6.

[6]强丽霞. 基于端点换重的装车地直达车流组织优化模型与算法研究[J]. 铁道学报，2009(6)：91-96.QIANG Li-xia. Model and Algorithm of Optimized Organization Scheme for Through Trains from Loading Points based on Endpoint-for-weight[J]. Journal of the China Railway Society，2009(6)：91-96.

[7]冯芬玲，周广富，李华锋. 基于粗糙集的铁路货运服务质量评价研究[J]. 铁道货运，2016，34(9)：19-23.FENG Fen-ling，ZHOU Guang-fu，LI Hua-feng. Research on Service Quality Evaluation of Railway Freight Transportation based on Rough Set[J]. Railway Freight Transport，2016，34 (9)：19-23.

[8]钟伟民，牛进伟，梁 毅，等. 多策略果蝇优化算法及其应用[J]. 化工学报，2015(12)：4888-4894.

[9]王克甫，薛 鹏，黄全振，等. 求解旅行商问题的改进果蝇算法[J]. 计算机工程与设计，2014，8(35)：2790-2794.

[10]范振平. 重载铁路通道车流吸引区域及始发直达重载化研究[D]. 北京：北京交通大学，2009.