初中平面几何教法探究

冯善照

(广东省江门市新会第四中学 529145)

在实际课堂教学中，看到不少学生在学习代数时成绩比较好，但一学平面几何，就不尽人意，主要是由“数”转到“形”的学习，从代数运算为主入几何推理为主，确实需要一段适应的过程.下面谈谈笔者对平面几何教学的一些看法.

一、狠抓概念、定理的教学

概念定理是几何教学的基础，是数学推理论证的依据，抓好这个环节的教学是培养学生思维的必由之路.但如何抓概念教学呢？1.注重概念、定理的发生和发现过程.重视从具体实例引入概念、定理，引导学生从感知材料中，领悟到概念、定理的本质.如在教授直线概念时，让学生看图并口述直线的概念，引导他们思考，从而发现直线的延伸性，掌握它的本质；2.注重强化概念、定理的练习.例如为了强化线段这个概念，让学生在下列图形中找出各有几条线段，这就使学生对线段加深了认识；3.加强概念、定理的应用.如学习等腰三角形的两个底角相等这一定理后，最好由简单到复杂配置一定的例题、习题让学生思考,例如：

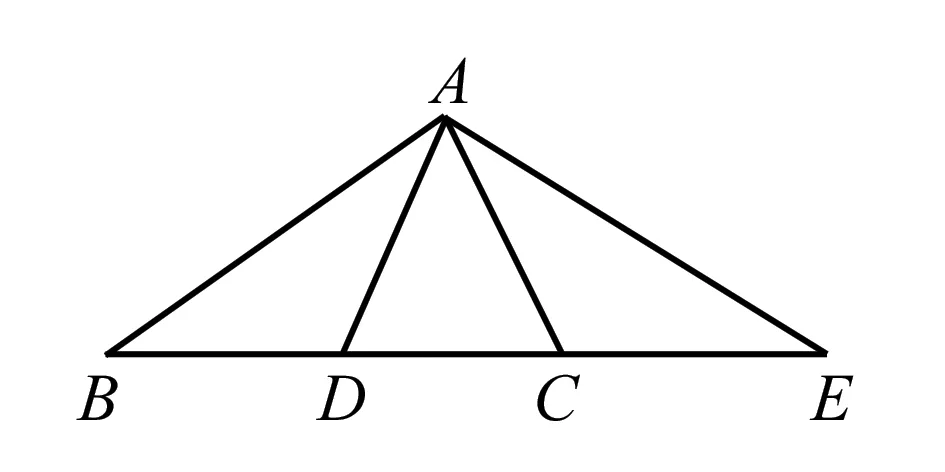
(1)在△ABC中，AB=AC，∠A=80°，求∠B，∠C.

(2)在等腰三角形中，有一个角等于70度，求另外两个角.

(3)如图，已知AB=DB，AC=EC，∠ABC=50°，∠ACB=70°，求∠D和∠E

这就使学生逐层地掌握好等腰三角形这个性质，起到强化概念、定理应用的作用.

二、重视识图、作图的训练

几何主要研究图形的关系，要提高教学实效，一定要抓好识图及作图的训练.

首先是培养看图能力.初学几何时，学生对于一些易位图、重叠图看不惯，这就应注意常规图的训练，以激发其学习的兴趣.

如：1.图中共有几条射线？请用两个大写字母表示出来.

2.右图中有几个直角、平角、锐角、钝角？

3.在下列图中找对顶角.

在培养学生看图能力同时，也要注意引导学生根据文字叙述画出图来，通过一定的训练，使学生逐步能把几何图形和几何命题结合起来.

其次是正确规范画图.几何作图教学中，正确规范画图，不但可以使学生正确理解概念，而且是学好几何的至关重要一环.在教学中应注意表率作用，对教学中的一切图形均当场示范，所画的图形要有普遍性，从易到难，培养学生的作图能力和正确作图素质.在讲作图时，先示范，再让学生跟着一步一步地作，这样培养学生正确作图能力.

再次要培养学生“用图”的意识.从感知的角度来看，往往比较复杂的图形学生难于看懂，在看题目的过程中，要让学生用适当的方法在图中作标记，将已知条件和要求的结论尽量放到图形中.如表示平行可用箭头，表示相等用相同的短线，相等的角用相同的弧线，线段的长度用相应的数值，要求证或求解的用“？”等.

例如下题:

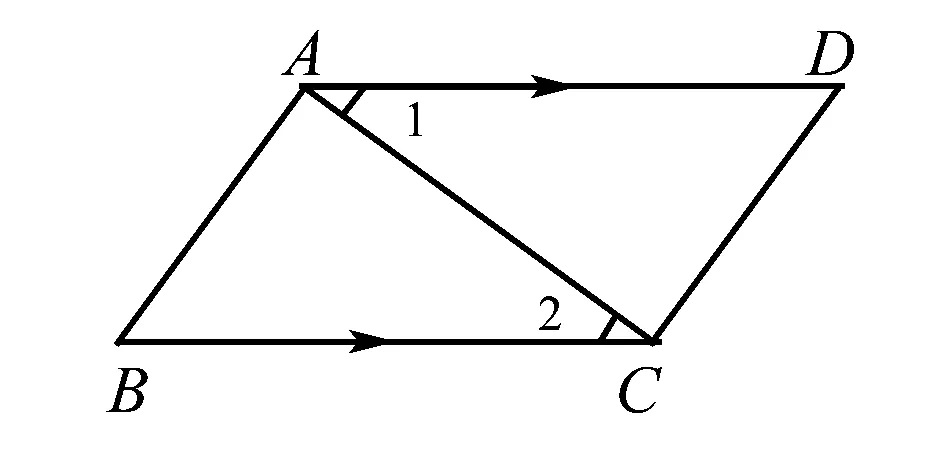
已知：四边形ABCD,AD∥BC，AD=BC.

求证：AB=CD.

就用如右图的方法把已知和求证在图中表示出来，加强直观性，更容易找出思考证明方法.要培养学生合理运用图形解题的意识，为推理能力的培养奠定坚实的基础.

三、注重推理能力的培养

几何教学的主要任务是培养学生的逻辑推理能力，使学生通过学习初步具备一定的推理能力.为此，首先要抓紧初步推理能力的培养，初步推理指的是推理填空及简单的一步推理练习，这部分是在平行线、相交线这章完成，要求学生掌握会填写好推理填空的根据，并教会学生几何语言的运用；另外要求学生能运用平行线的性质进行计算，在这基础上提前引入下一章一些适当的例题、习题及定理证明改写成推理填空，这对学生的推理能力的培养有很大的帮助，并为下一步书写证明过程做好准备；再就是要培养学生的分析能力.学生是否顺利地进行推理和论证，很大程度上取决于学生是否掌握分析题目的方法，学生刚开始学习推理，未能掌握一定的方法，在教学过程中为能使学生更清晰看懂，用“分析图”来引导效果较好，从结论出发，一步一步地“逆向”推出使每一级结论成立的充分条件，直接到题设，从而打通思路.例如：

已知：如图AB=AC，D、E分别是AB、AC上一点，CD、BE交于O，且∠B=∠C.求证：BD=CE.

分析

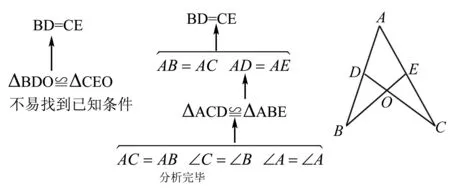
这样使学生思路清晰，在这基础上再让学生由最后倒写上去，从而能写好证明过程.

四、加强创造性思维培养

为使学生的思维能力达到更高的层次，故在数学教学，尤其在几何教学中要培养学生的创造性思维，这也是适应素质教育的要求.

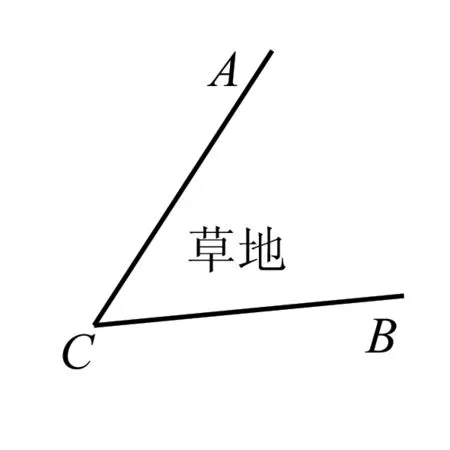
首先要善于创设问题情境，引导学生发现问题.如在讲“三角形两边之大于第三边”时这样提问，有一块草地，旁边树了一个写着“请脚下留情”的牌子，如右图，本来由点A到点B是有路可走的(可先经点C再到点B)，而还是有人贪方便直接从草地经过，这是什么原因呢？通过这样鲜活的例子，引导学生总结出三角形的三边关系，从而使学生加深对知识的理解.

其次要善于引导学生进行类比，展示思维的过程.例如学习等腰三角形性质时，可先复习等腰三角形的定义，再让学生找出相等的边及相等的边所对的角(底角)，再让学生量一量底角的度数，得出等腰三角形两个底角相等，再让学生去论证，这样就能培养学生的创造性思维.

再次要善于组织问题链，引导学生探索.对于几何中一些基本题的讨论、推广和引伸，就形成了问题链，问题链的结构具有联系性又具发展性，它对培养学生的创造性思维很有好处.

例如下面的例题.

已知：平行四边形ABCD中，对角线AC和BD相交于O，M、N分别是OA、OC的中点.

求证：BM=DN，BM∥DN.

可以组织以下的问题链，已知不变.

求证：(1)△OBM≌△ODN;

(2)∠BMO=∠DNO;

(3)BM=DN，BM∥DN.

另外提出问题让学生思考，以后有更好的方法证明这道例题.

这样每解决一个问题，就提出新的问题，通过逐个得出后面的结论，让学生在不断的探索中培养创造性思维.

参考文献：

[1]杨文春.提升初中数学教学有效性的策略研究[J].考试周刊, 2017(25).

[2]陆栋.学生思维能力在初中数学教学中的全面发展[J].数学学习与研究,2017(03).