例谈基于问题解决的初中数学复习

黄书旺

(福建省闽清县城关中学 350800)

笔者经历了多轮初三数学复习的教学实践，对初三复习课进行了大胆地改革创新，以基于问题的解决来设计所复习的知识内容，引领学生进行自主探究，发现式地进行复习，让学生感受到复习的内容虽源自于课本，但却高于课本，对课本固有的知识内容的理解“柳暗花明又一村”，对复习课兴趣倍增，教学效果显著，历年中考成绩菲然.

下面笔者就一节 《三角形全等的判定》 的复习课来谈谈基于问题解决的初中数学复习法.

问题1 如图，已知：在△ABC和△ABD中，AC=AD，∠C=∠D.求证：BC=BD.

学生活动：自主探究证明方法.

预设错解部分学生经验使然，直接证明：在△ABC和△ABD中，AC=AD，∠C=∠D，AB=AB，∴△ABC≌△ABD(SAS)，∴BC=BD.

错因分析要准确理解“SAS”作为三角形全等的判定定理的内涵，两边一角对应相等判定两个三角形全等时，此角必须是相等两边的夹角，若此角是其中一边的对角时，两个三角形不一定全等.

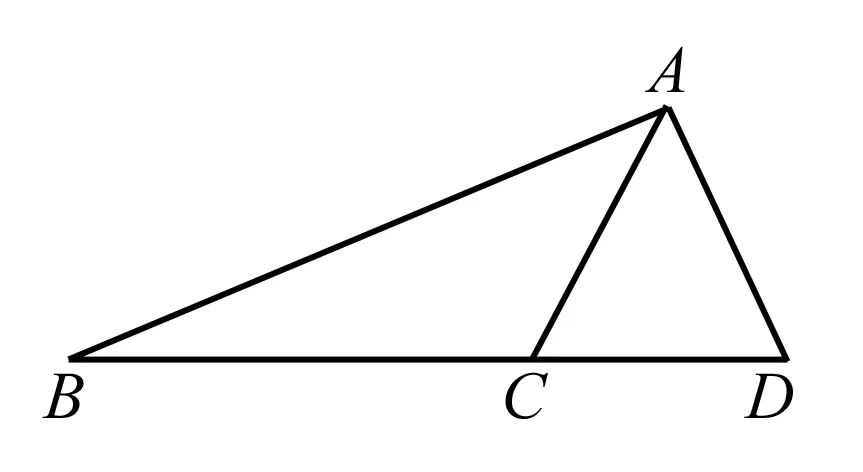
解法指导引导学生重温人教版八年级数学(上)P39的课本内容：“如图，把一长一短的两根木棍的一端固定在一起，摆出△ABC.固定住长木棍，转动短木棍，得到△ABD.这个实验说明了什么？”

学生齐答：有两边和其中一边的对角分别相等的两个三角形不一定全等.

教师点评：问题1是源引人教版八上课本P39“思考”中操作实验为蓝本，对教材的内容进行二次创造，让教师在教学中容易乎略而又能引起学生产生争议的问题得到有效的开发和利用，激发起了学生的好奇心和探究欲望.课本实验的结果为什么说两个三角形满足“SSA”不一定全等，而不是说不全等，它有什么玄机吗？在平时判定三角形全等的教学中教师是“明令禁止”学生使用“SSA”的，到底为什么呢？大部分学生也认为用“SSA”来判定三角形全等是错误的，只有一小部分学生认为可以用“SSA”来判定三角形全等.在平常作业或练习中又有许多学生都在不知不觉中应用了“SSA”来判定三角形全等.因此，本题看似一道简单的证明题，却能很好地反映学生对三角形全等判定定理掌握和理解的程度，同时又能给一些学习上有自满倾向的学生一个“顿悟”，激起学习、探究的欲望.

问题2 看来，如果在△ABC和△DEF中，已知：AC=DF，BC=EF，∠B=∠E，有可能“△ABC≌△DEF” 或“△ABC与△DEF不全等两种情况是吗？

下面，我们不妨对∠B进行分类，可分为“∠B是直角、钝角、锐角”三种情况进行探究．

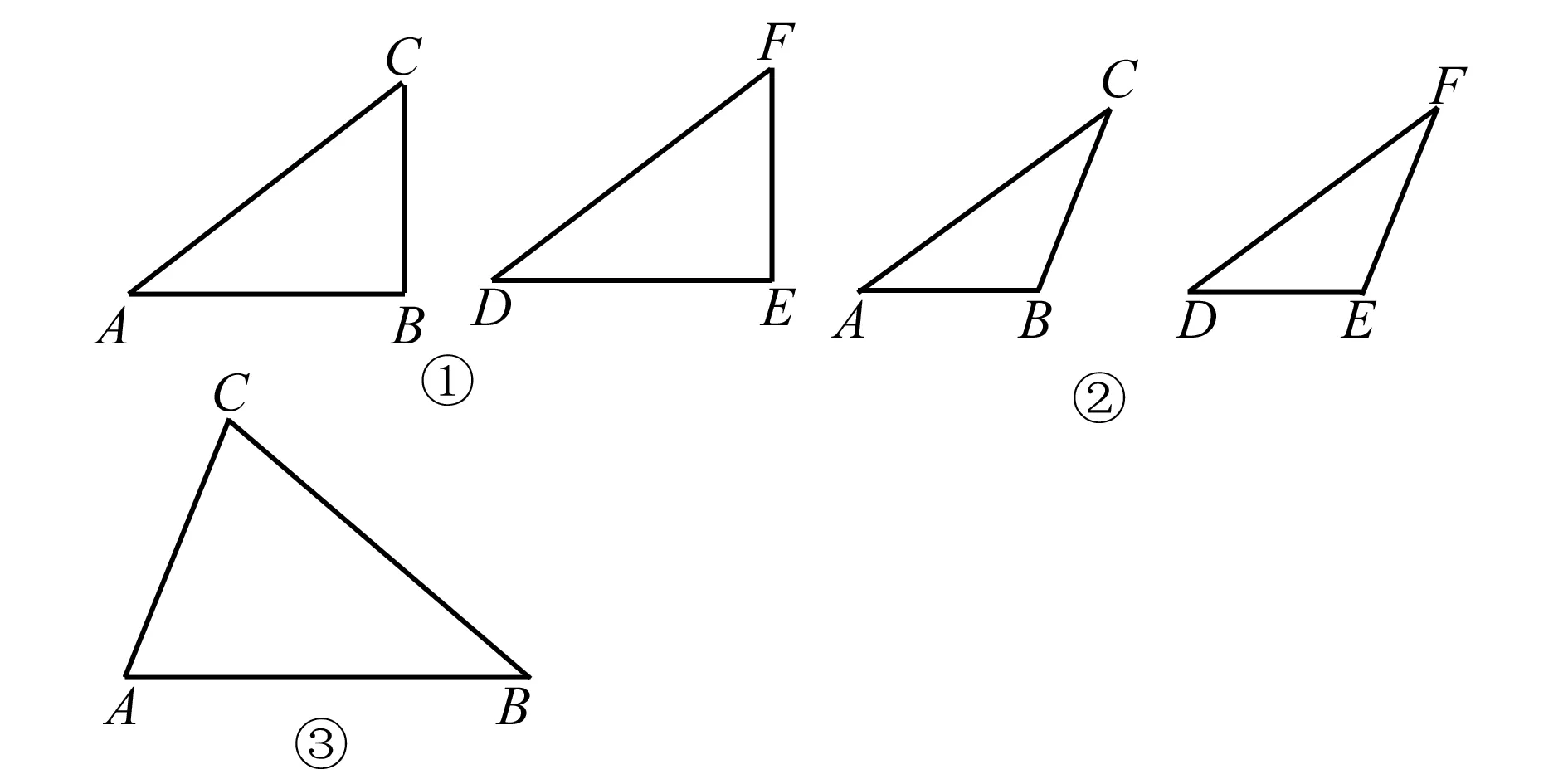
学生活动：第一种情况：当∠B是直角时.

如图①，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E=90°，根据 ，可以知道Rt△ABC≌Rt△DEF．

预设解法：显然，学生较易根据直角三角形全等的判定方法“HL”可证明；因为两个直角三角形中有直角边(BC和EF)和斜边(AC和DF)对应相等的两个直角三角形全等.也就是说，当∠B是直角时，△ABC≌△DEF．

教师点评：为什么不直接解决问题1，而先提出问题2让学生来思考，是有意课堂节奏慢下来，让学生从易证的问题入手，探索、研讨问题1的解决方法，为解决问题1埋下伏笔.同时也给学生解决问题增强一点信心.

学生活动：第二种情况：当∠B是钝角时，求证：△ABC≌△DEF．

如图②，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是钝角，求证：△ABC≌△DEF．

预设解法学生由于有了第一种情况(当∠B是直角时)的证题经验，可以通过交流、讨论，合作，探索了通过添加高线，将钝角三角形转变为直角三角形，仿造第一种情况来证题.

解法指导证明：如下图，过点C作CG⊥AB交AB的延长线于G，过点F作FH⊥DE交DE的延长线于H.

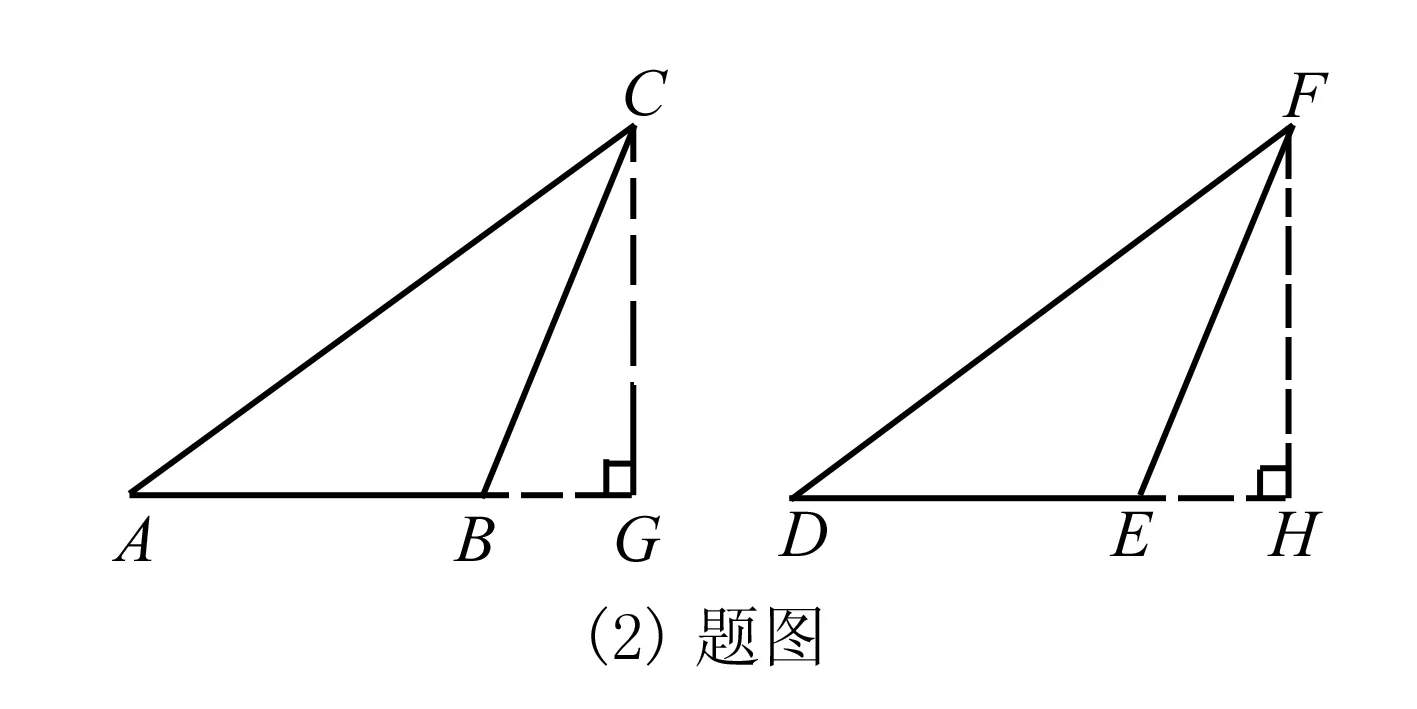
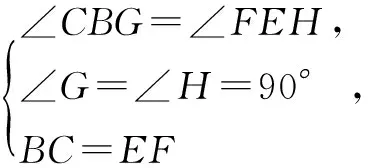
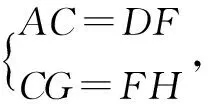
教师点评将疑难的问题简单化、特殊化是启迪学生思维的一种良好的方法，教学中教师引导学生先分为“∠B是直角、钝角”二种情况进行探究，看看会有什么样的结果.学生根据“HL”易证出满足“SSA”的两个直角三角形全等，进而将这种思路迁移至满足“SSA”的两个钝角三角形全等.让学生得到意想不到的结论，即能用“SSA”来证明两个均为直角三角形或两个均为钝角三角形的特殊三角形是全等的，给学生以惊喜、以思维定势上的颠覆，让学生初步尝试到成功的喜悦，为后续的探究提供动力，积累经验.但在平时复习课教学中，我们教师总是急于求成，设置的问题往往“高、大、难”，让学生可望而不可及，望而生畏，久而久之学生便果失去探究的兴趣，扼杀了学生思维的能动性和创新性.

学生活动：第三种情况：当∠B是锐角时，情况又会是怎么样呢？△ABC和△DEF还会全等吗？如果全等，请加以证明；如果不会全等，请画出图形并加以说明.

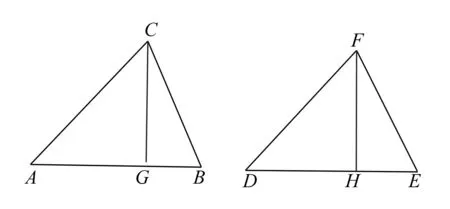
预设解法：如图,分别过点C作CG⊥AB交AB于G，过点F作FH⊥DE交DE于H，仿造第二种情况就证出来了.

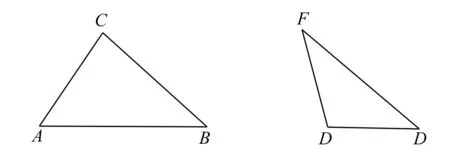
错因分析如图.明显地，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是锐角，△ABC是锐角三角形，而△DEF却是钝角三角形，这是不能够全等的.

教师点评将∠B改为锐角，一部分学生可能受思维定势第一、二种情况的影响，误认为当∠B为锐角时，两个三角形均为锐角三角形，而轻易得出满足“SSA”的两个锐角三角形全等，而乎略了当∠B为锐角时，两个三角形可能还有其他类型，给学生以思维的严密性和批判性.

问题3 在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是锐角，请你用尺规在图中作出△DEF，使△DEF和△ABC不全等．(不写作法，保留作图痕迹)

学生活动：动手操作、画图.

解法指导作图如下：

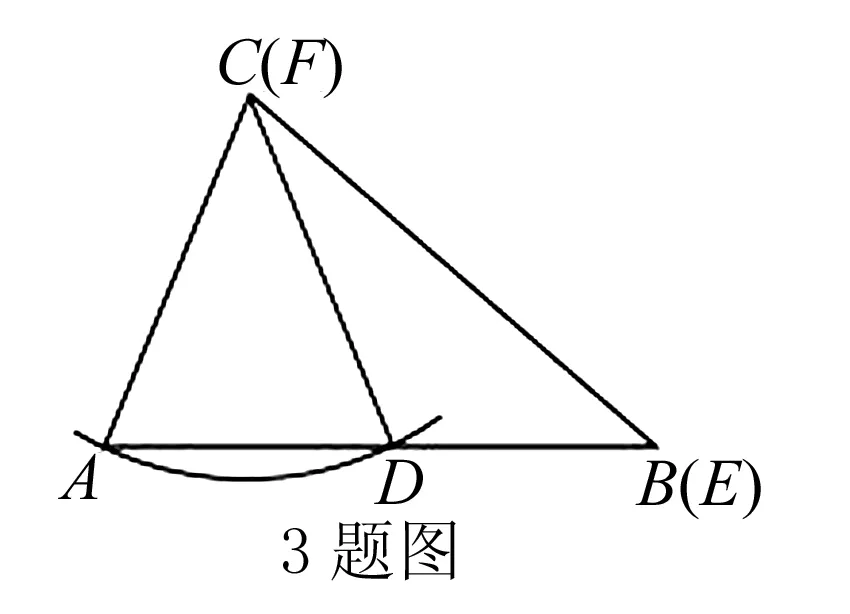
以点C为圆心，以AC长为半径画弧，与AB相交于点D，E与B重合，F与C重合，得到△DEF与△ABC不全等.

教师点评学生从作图中看出了△DEF和△ABC不全等的现象，这再一次重温、巩固了人教版数学八年级(上)P39的课本实验内容的本质及意义所在，弄清了问题的真相.

问题4 我们再来讨论一下：如果∠B(锐角)还要满足什么条件，就可以使△ABC≌△DEF？请直接写出结论：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是锐角，若∠B时，则△ABC≌△DEF.

学生活动：学生议论纷纷，踊跃发言.

预设解法：1.当∠B=∠A时，则△ABC≌△DEF．这时△ABC和△DEF都是等腰三角形．显然△ABC≌△DEF．

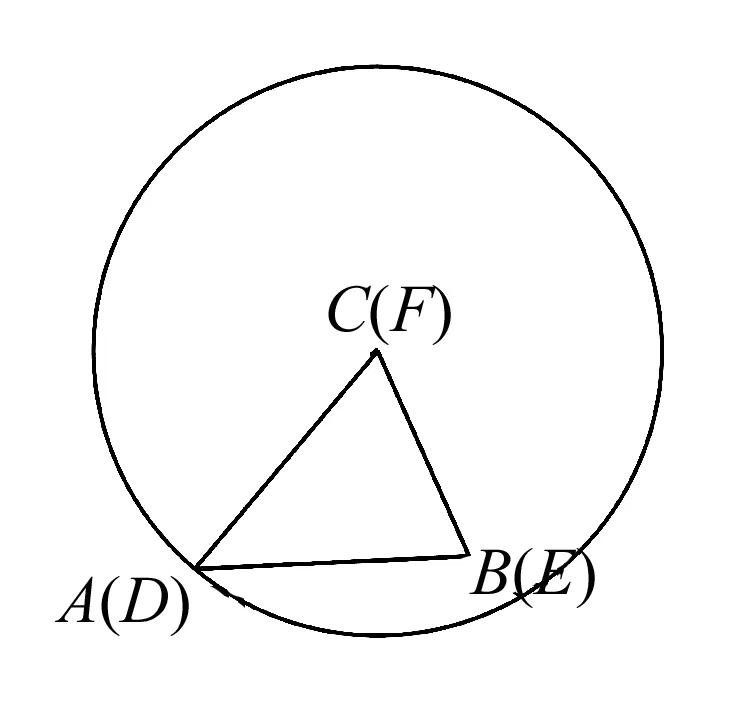
2.当∠B>∠A时，则△ABC≌△DEF.

解法指导：从以上尺规作图中得到启发，如图，当∠B>∠A时，以点C为圆心，以AC长为半径画弧，与AB相交于点D，E与B重合，F与C重合，只可能得到△DEF与△ABC全等；也就是说，AC与AB边只有唯一的一个交点，所以△ABC≌△DEF.

我们也可以根据以上讨论过的三种情况的结论，得出∠B不小于∠A．即∠B≥∠A时，△ABC≌△DEF.

教师点评：从这里可以看出，我们的复习课教学不仅仅是要让学生听得懂，还要让学生真正理解所学过的知识，有必要让课堂教学节奏慢下来，认真落实课程理念，以基于问题解决为目标，尊重学生，注重探究教学.知识方法的生成，不能引导过度，要不惜时间充分引导学生自主发现，引导学生学会思考，真正做到把问题研究透彻化.

问题5 通过以上各种情况的探究，得出“两个三角形满足两边和其中一边的对角对应相等”，这两个三角会全等的情形条件，同学们能用简洁的语言加以概括吗？

学生活动：众说纷纭.

解法指导：当两个三角形是同类三角形且满足边边角时，可认为两个三角形全等.

问题6 当两个三角形满足“SSA”条件，证明其全等时，常添加什么辅助线呢？有什么规律吗？你能对问题1进行证明了吗？

学生活动：齐答：作高线！证明方法通常是：作第三边上高线即可证.

教师点评：让学生说说从以上的学习、探究过程中，自己的所思、所想、所悟，正是培养学生的概括和归纳能力所必须的，也是基于问题解决的一种经验总结，更是一种复习课效果的展现.

课堂总评：教材中的例习题一直是中考命题者的基点，本例题源于教材，是对教材的二次开发与利用，已经凸显为其多维度的生长点.我们教师在平时复习课中要善于钻研教材，基于复习课中问题的解决，提升教材中例习题教学价值，要有善于迎合、运用中考题做变式迁移的设计，提取核心知识与方法能力和整合教学资源的意识，这正是我们教师复习课教学中所缺失的，但又是非常需求的.平常复习课教学中，我们大部分教师缺乏以教材例习题为依托，在原题的基础上进行改编、创新与拓展的精力和能力.通过本例题的教学，一方面引领教师在日常复习教学中要研究教材、关注教材、深刻理解与把握教材；另一方面也启示学生在平时的学习中要重视课本，吃透课本中的例习题，尤其是课本中的思考与拓展部分的内容所蕴藏的能量与价值.基于问题的解决，创新复习课教学，提高复习课堂效率，必然对初中数学的教与学整体性的导向是一个强有力的引领.

参考文献：

[1]季文珠.“探索三角形全等的条件”教学案例[J]. 数理化学习(初中版)，2014(05).