基于扩展结构相似性的特征匹配方法

, ,

(1.重庆工程学院 科技处,重庆 400056; 2.重庆市数字影视与新媒体工程技术研究中心,重庆 400056)

0 概述

从图像和视频中提取特征进行匹配或比较,是计算机视觉处理的基本过程,可应用于关键点匹配[1-2]、信息检索[3]和信息分类[4]等方面。近些年,特征匹配也广泛应用于场景解析或通过SIFT flow进行的光流估计中。相似性度量方法基于特征之间的相似性实现特征匹配,随着特征提取方法的发展,相似性度量方法的研究成为热点。

欧式距离是最常用的相似性度量方法,其计算特征向量在欧式空间的二范数距离[5]。然而,取决特征提取方法的差异性,特征向量并非遍及整个欧氏空间分布,而是局限于该特征相应提取方法内在约束的子空间。因此,通过利用特征的内在特性,欧式距离之外的相似性度量方法被提出。衍生自统计学卡方检验的卡方距离[6]是一种常用的基于直方图特征的度量方法,其也可利用核函数进行处理[7]。为了解决运输的优化问题,文献[8]提出推土机距离以对直方图特征之间的相异性进行有效的度量,但该方法需要耗费极大的计算成本。欧式距离和卡方距离仅仅由直方图相应组中的差分所组成,推土机距离则考虑到直方图的组间关系。扩散距离度量方法也应用这样的跨组距离思想,其基于直方图特征的结构而非一个简单的向量[9-10]。

作为与特征匹配相近的领域,图像质量评价要求图像间相似性度量方法应与人类感知相近。而欧式距离与人类感知不相容,并不适用于图像相似性度量。研究人员根据人类视觉系统提出了结构相似性(Structural Similarity,SSIM)度量[11-12]。与人类的视觉过程相同,该方法通过利用图像分块间的结构特征,对参考图像与其畸变图像之间的相似性进行度量。但SSIM度量方法局限于结构化阵列形式,鲁棒性较差,而特征匹配则对鲁棒性要求较高。

针对上述问题,本文不局限于非负数的直方图形式,提出一种多维向量结构的相似性度量方法——扩展结构相似性(Extended Structural Similarity,ESSIM)。在网格空间中提取局部基元特征的三阶张量,并将该种特征结构应用于相似性度量中,以提高其鲁棒性并保留SSIM的辨识能力。

1 结构相似性

本文主要介绍在图像质量评价中SSIM的公式化表示,及其对特征匹配的适用性。已知参考图像Ix,通过对目标图像Iy与Ix间的相似性进行度量,以对Xy的图像质量进行评价。SSIM分别从图像Ix和Iy中提取成对图像分块x和y,计算式(1)的相似性度量值S;然后,对整个图像的分块得分S求平均,得到图像Ix和Iy间的相似度。

S(x,y)=l(x,y)c(x,y)s(x,y)

(1)

l(x,y)=k(u(x),u(y))

(2)

c(x,y)=k(q(x),q(y))

(3)

(4)

(5)

在式(1)～式(5)中,u(x)和q(x)分别为图像块x和y中像素的均值和标准偏差函数,k(a,b)为标量a和b间的相似性测量函数。

函数l、c和s分别对图像分块中的亮度、对比度和结构信息的相似度进行测量。与跨组距离类似,结构相似度s(x,y)提取像素间的相关系数,其对于像素间的仿射关系(yi=αxi+β,(α>0))总是给出最大相似性得分(即等于1),所以对像素变化的鲁棒性过高,不能给出令人满意的相似性度量结果。对其进行补偿,引入相似度l和c,以捕捉亮度变化(偏差β)和对比度变化(比例α),这些度量方式均与人类感知系统相关。

同时,作为欧氏空间中的一种简单的相似性度量方式,点积可以进行式(6)所示的分解。

xTy=D{q(x)q(y)s(x,y)+u(x)u(y)}

(6)

与式(1)形式不同,但具有相关性,即亮度和对比度相似性分别退化为简单积u(x)u(y)和q(x)q(y)。可以看出,亮度相似性被分离为一种加法形式,这种公式化表示存在于SSIM变体中[13]。因此,基于式(1)和式(4)的比较,可以得出SSIM的出色性能很大程度上基于式(5)的处理。

2 本文方法

本文基于SSIM度量,提出一种新的用于特征匹配的相似性度量方法。最简单的方式是直接将特征向量x和y输入式(1)中进行匹配评价。这种方法的效果并不好,尽管特征匹配与图像质量评价都建立于相似性度量之上,但对鲁棒性的需求标准不同。SSIM通过对图像细微变化的有效表达,广泛应用于对目标图像的失真度测量;特征匹配要求对目标图像本身进行辨识,同时对畸变具有较高的鲁棒性。因此,本文结合SSIM的优势和特征匹配的要求,提出一种扩展结构相似性(Extended Structural Similarity,ESSIM)的特征相似性度量方法,其不仅保留了SSIM的辨识能力,同时提高了SSIM所缺少的鲁棒性。

传统方法假设特征为直方图形式,本文则将特征公式化到结构化形式,如三阶张量。本文提出的方法利用固有的特征结构,并改进相似性度量函数以提高特征鲁棒性。

2.1 特征结构

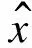
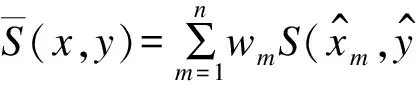
(7)

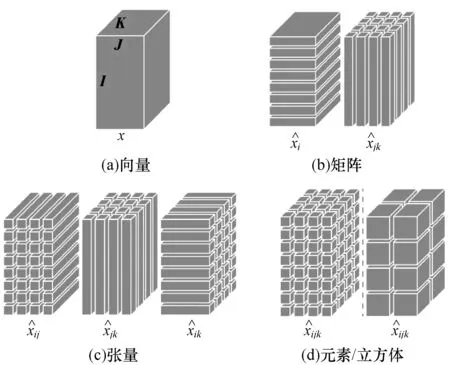
图1 子特征结构示意图

(8)

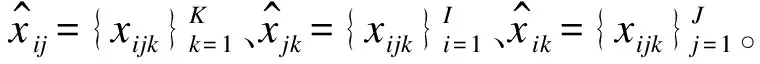
(9)

4)元素/立方体:在最小结构的情况下,本文将每个特征元素xijk设为子特征,则得出相似性度量如式(10)所示。

(10)

2.2 相似性度量

原始的SSIM定义为亮度均值l、对比度方差c和结果相关性s3种相似性函数的积,如式(11)所示。这三者共同的乘积对这些统计数据的任何畸变均具有敏感性,这有利于图像评价,但在特征匹配中则缺乏鲁棒性。从鲁棒性的角度出发,本文提出了式(11)的几种SSIM度量的变体,如式(12)～式(15)所示。

原始形式:

Sorg=l×c×s

(11)

分离l:

S+l=wll+ws(c×s)

(12)

分离c:

S+c=wcc+ws(l×s)

(13)

分离s:

S+s=wss+wl(l×c)

(14)

全相加:

Sadd=wll+wcc+wss

(15)

式中引入权值,以平衡加和形式。式(12)与式(6)结构相同,将相似性的亮度均值l分离到加性项内。这些权值基于相似性函数的数值范围而确定,如式(16)所示。

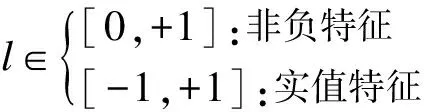
(16)

如果扰动孤立地出现在l、c和s3项中,则全相加形式Sadd可最大限度地抑制其对最终相似性度量的影响。因此,本文使用张量结构(式(9))的全相加相似性度量方法(式(15)),其通过加和形式提高鲁棒性,并且有利于特征映射进行降维处理。

2.3 显式特征映射

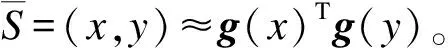
(17)

(18)

3 实验结果与分析

本文实验首先通过关键点匹配对本文方法的性能进行分析,然后应用于图像检索。

3.1 关键点匹配

本节实验测试本文方法对局部描述子特征的关键点匹配的性能。局部描述子通常利用局部空间布局公式化一个结构化张量。本文使用SIFT的三阶张量空间布局8(I)×4(J)×4(k);对Mikolajczyk & Schmid数据集进行实验;该数据集包括8个图像集,每个集合由1个参考图像和5个从不同角度和尺寸捕捉到的畸变图像。本文基于平均精度,即正确匹配的描述子对的比例对性能进行评价。

3.1.1 特征结构

本节实验统一使用式(11)相似性度量S=Sorg对不同类型的子特征结构(如图1所示)进行评估。以张量结构为基础,与其他子特征结构进行比较,结果如图2所示。横轴和纵轴的坐标分别表示2种比较方法对每个图像分块的平均精度;点“O”落在坐标系的上半部分表示纵轴结构的性能较好,反之横轴结构性能较好;所有的纵轴均表示张量结构。

如图2所示,张量结构的性能优于其他类型的结构;尤其是其性能显著优于向量结构。虽然矩阵结构性能低于张量结构,但均超过了向量结构和元素结构,后两者则完全没有考虑到SIFT特征的结构性。这一结果证明了将特征结构纳入相似性度量是一种有效的手段。立方体结构利用了这种结构特性,对于相似性度量形成具有一致性的子特征比较重要,在张量结构中,沿着各自维度的子特征具有一致性,而立方体结构则在子特征中混合了所有的3个维度。

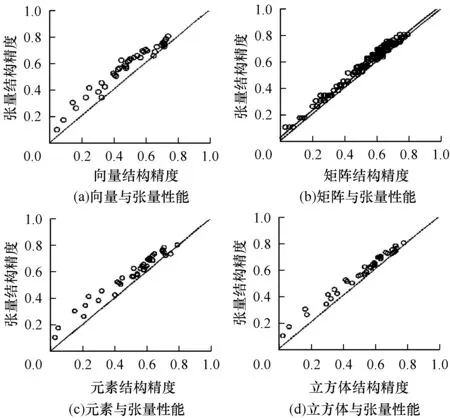
图2 子特征结构性能比较

3.1.2 相似性度量函数

本节实验主要分析张量结构情况时,各相似性度量形式S。在实验中,将不同类型的相似性度量函数(式(10)～式(15))与本文主要关注的Sadd进行了比较,结果如图3所示。由图3(a)可以看出,Sadd的性能明显优于Sorg,所以将原始的SSIM公式Sorg展开到相加形式,在提高性能表现的同时也增加了鲁棒性。由图3(b)～图3(c)可以看出,S+l、S+c和S+s3种加和形式的性能大致相当,但仍比Sadd稍逊一筹,并且Sadd生成的显式特征映射的维数最低,计算效率优于其他加和形式。所以,在接下来的实验中,均取Sadd形式,同时权值设置为{wl,wc,ws}={2,2,1}。

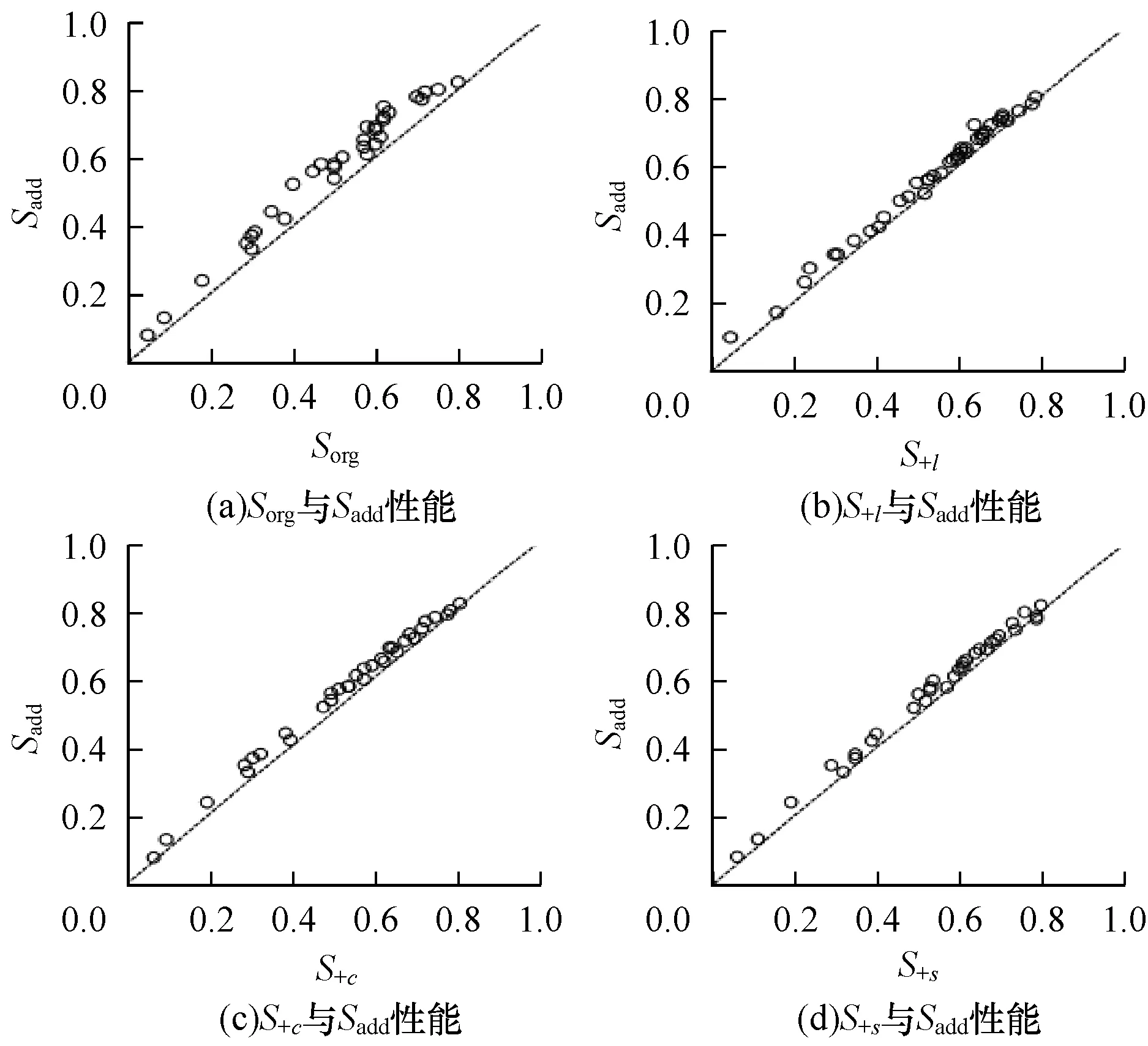
图3 不同相似性度量函数性能比较

3.1.3 本文方法与其他方法比较

本节实验将本文方法与欧式距离、卡方距离、扩散距离和推土机距离度量的传统方法进行比较;除欧式距离,其他传统方法均基于直方图形式。关键点匹配结果如图4所示,其中纵轴均表示本文方法。

图4 不同方法关键点匹配结果

由图4可以看出,本文方法的性能优于其他方法。实验结果表明:基于本文特征结构方法的性能优于传统直方图形式;与图4(c)扩散距离相比较,基于SSIM的度量适用于对跨组相似度的提取。

为了进一步说明本文方法的性能,下文比较各方法相似性度量的计算时间。实验以Matlab(版本为2014b)为平台,利用Matlab mex-C混编文件实现;处理器为英特尔Xeon 3.4 GHz;操作系统为64位Windows7。实验比较每个样本对的平均计算时间,结果如表1所示。从表1可以看出,本文方法利用点积形式的显式特征映射,显著加快计算时间;计算时间比欧式距离度量之外的其他方法大幅度降低。

表1 不同方法的平均相似性度量计算时间 ns

3.2 图像检索

图像检索为特征匹配的重要应用,本部分实验进一步对本文方法图像检索性能进行测试。3.1节的关键点匹配是对同一个目标的参考图像和畸变图像进行比较;与此不同,图像检索对不同目标、不同图像间的相似性进行度量,这就要求对畸变具有较高的鲁棒性,并对相似性度量在目标识别方面的性能进行评价。

本节实验通过DoG检测器提取SIFT特征,对建筑物数据集进行检索实验,并与传统方法进行比较。各方法的图像检索准确率如表2所示,可以看出,本文方法的图像检索准确率较其他传统方法明显提高,达到81.5%,表明本文的相似性度量能够有效进行目标辨识。

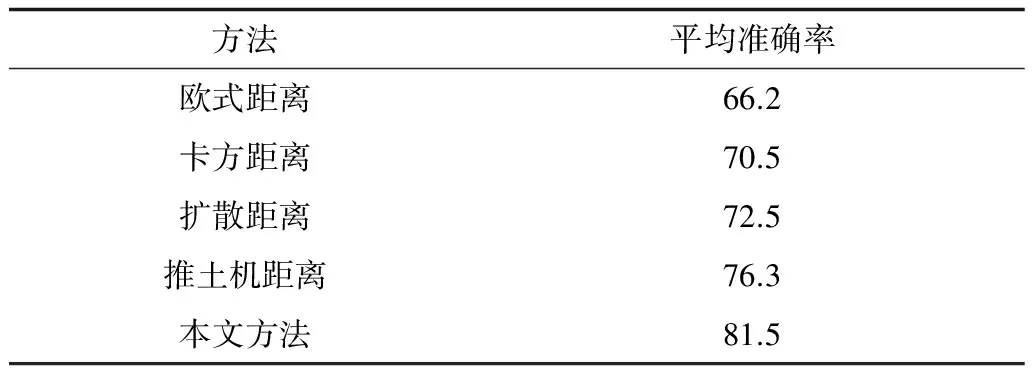
表2 不同方法图像检索准确率比较 %

4 结束语

本文提出一种以测量成对结构化特征间的相似性方法用于特征匹配。提取局部基元特征的三阶张量,将该内在结构特征与在图像质量评价中广泛应用的SSIM相结合,提出具有高鲁棒性的相似性度量方法——扩展结构相似性度量。同时,本文利用显式特征映射,将特征作为点积嵌入,以显著提高相似性度量的处理速度。实验结果表明,本文方法在特征匹配的应用中具有良好的性能,同时具有较高的计算效率。

[1] 张宇仁.图匹配算法及其在月面图片关键点匹配中的应用[D].北京:中国科学院大学,2016.

[2] 高洪波,王洪玉,刘晓凯.一种基于分层学习的关键点匹配算法[J].电子与信息学报,2013,35(11):2751-2757.

[3] BALA A,KAUR T.Local texton XOR patterns:a new feature descriptor for content-based image retrieval[J].Engineering Science & Technology International Journal,2015,19(1):101-112.

[4] AKATA Z,PERRONNIN F,HARCHAOUI Z.Good practice in large-scale learning for image classification[J].IEEE Transactions on Software Engineering,2014,36(3):507-520.

[5] 刘相滨,邹北骥,孙家广.基于边界跟踪的快速欧式距离变换算法[J].计算机学报,2016,29(2):317-323.

[6] 郑 倩,卢振泰,陈 超.基于邻域信息和高斯加权卡方距离的脊椎MR图像分割[J].中国生物医学工程学报,2011,30(3):357-362.

[7] DALIRI M R.Chi-square distance kernel of the gaits for the diagnosis of Parkinson’s disease[J].Biomedical Signal Processing & Control,2013,8(1):66-70.

[8] 韩 华,曹 伟,龚 涛.目标再确认中基于推土机距离的关联度建立[J].华中科技大学学报(自然科学版),2015,22(3):435-439.

[9] 贡 超,蒋建国,齐美彬.基于扩散距离的SURF特征图像匹配算法[J].合肥工业大学学报(自然科学版),2015,22(4):449-478.

[10] 卞程飞,张 健,吴 娜.基于可移动窗口和扩散距离的立体匹配算法[J].系统仿真学报,2014,26(9):2130-2135.

[11] WANG Z,BOVIK A C,SIMONCLLI E P.Image quality assessment:from error visibility to structural similarity[J].IEEE Transactions on Image Processing,2004,13(4):600-612.

[12] 袁艳春,刘云鹏,高宏伟.基于边缘结构相似性的图像质量评价方法[J].计算机应用研究,2015,32(9):2870-2873.

[13] BRUNET D,VRSCAY E R,WANG Z.On the mathe-matical properties of the structural similarity index[J].IEEE Transactions on Image Processing,2012,21(4):1488-1499.

[14] WU X,TANG Y,BU W.Offline text-independent writer identification based on scale invariant feature transform[J].IEEE Transactions on Information Forensics & Security,2014,9(3):526-536.

[15] 贾世杰.基于内容的商品图像分类方法研究[D].大连:大连理工大学,2013.