基于移动大数据的城市深夜公交线路改进方案

李贞镐,

(清华大学 电子工程系,北京 100084)

0 概述

随着大城市全球化进程的加快和地域时差的影响,需要深夜工作的人数持续增加。特别是对于世界经济同步增长的大城市来讲,为保障夜间出行人群使用大众交通工具的需求,开设深夜公交线路显得尤为重要。当前,中国的大城市大都设有深夜公交路线,但普遍存在运营效率低、运输成本高、涵盖范围不够等诸多问题[1]。随着大城市人口不断增加,利用建设卫星城疏导人群是一种趋势。以上海为例,设有松江、嘉定、安亭、金山卫和吴淞等卫星城,但连接这些卫星城的深夜公交线路却非常缺乏。

近年来,计算机技术迅猛发展,特别是以智能终端和社交媒体为代表的各种信息渠道的出现和信息的生产、流通、保有量的持续增长,大数据的概念越来越受到人们的重视[2]。

因为大数据中存在大量的无效信息,所以从中筛选出有用的信息非常重要。可视化作为大数据分析中最重要环节之一,其目的就是大数据分析结果可以通过视觉上容易理解的方式表达和传递[3]。可视化作为大数据中提取有价值信息的核心技术,是大数据处理过程中必不可少的环节。而且,随着大数据处理和分析技术的发展,对既有大众交通线网进行有效的评价及优化,促进城市交通智能化管理健康发展。

大多数公交线路评价方法选取重复度为评价指标,但该方法在计算过程中对评价区间距离的定义不明确,而且,根据被选为评价基准的线路不同,其评价结果之间具有巨大的差异[4]。考虑区域均衡性的公交线路评价模型,目的是为了达到整个公交系统的均衡分布,确保公交线网较高的覆盖程度,适合以城市整体公交线网的评估[5]。

本文在上海市深夜公交线网优化的基础上,利用可视化分析软件,结合区域间均衡性模型方法和Dijkstra模型,研究基于移动数据及出租车移动数据的城市深夜公交线网评价及优化系统,分析上海既有深夜公交线网的问题并提出改进方案,为设计更高效的深夜公共交通线路提供有效的依据。

1 研究现状

公交线路的重复度是指在大众交通工具的运营中更有效的管理公交线路,即乘客使用起来更为便利的角度指定的评价指标,表示公交线路在特定区域或区间内的集中程度的指标。公交线路的过度重复会影响公交运营的效率,还会影响乘客选择乘坐路线[6]。

大多数公交线路的重复度评价方法是依据特定线路的区间长度,选取该区间内运营多少公交线路为判断指标,但这种方法在计算过程中具有一定的问题[7]。

首先,对评价区间距离的定义不明确。有的是计算整个线路的重复度,有的则是分成n个小区间进行计算。这2种方法的结果存在一定的差异,区间距离越小,重复线路越多,重复度指标也随即偏高。其次,根据被选为公交路线评价对比基准的线路不同,重复度评价结果也不同。总地来说,考虑到该方法不能彻底解决公交线路重复度评价中的问题,因此,本文研究选取考虑区域均衡性的公交线路评价模型。

2 上海深夜交通现况分析及优化设计

2.1 深夜移动需求数据的获取

在本文研究中,使用的数据集为上海移动网络供应商提供的2014年8月1日—31日的数据统计。数据集是针对全市设置的各个基站每10 min的数据量与对应的基站接收数据次数组成的三维矩阵。基站的数据集总共包含20亿条,总容量为8 GB,数据集容量虽然很庞大,但其信息的来源具有很高的可靠性。

深夜公交移动需求量分析中使用的数据信息主要包括3种:

1)上海市主要移动网络供应商用户的追踪数据集,每一个数据项记录用户名,每一次手机业务的开始和结束的时间、连接的基站编号以及消耗的流量等,数据集有超过19.6亿条记录,覆盖38万个基站。

2)上海出租车运营公司提供的数据集,记录了上海市1.3万辆出租车的移动轨迹数据,采用经纬度标示,时间跨度为1个月(2014年8月1日—31日),时间精度为1 min。

3)上海市地图,由百度地图下载,处理数据中选用精度为200 m。

2.2 考虑区域均衡性的公交线路评价模型

本文对既有深夜公交线路进行评价时,主要考虑了线路的重复性和覆盖程度,选用深夜公交线路的区域分布均匀程度为评价指标。在评价时,通过每个区域人口对比该区域深夜公交线路数量比值的差异,分析了深夜公交线路的区域均衡程度。

为了更好地观察移动需求量的变化,本文以移动数据的变化量代替移动数据量。并且根据实际测量,经过某一地区的公交线路周围移动数据变化量除以该地区移动人口数量的结果,作为公交线路均衡性的判定指标[8]。

A=∑Dt+1-Dt/S

U=A/B

(1)

其中,A为按时间测定的区域内平均移动数据变化量,D为按时间测定的移动数据量,t为时间(每隔10 min),S为区域面积,U为某一地区的公交线路分布均匀程度,B为人口。

单个公交线路的重复度Ri=1.0表示该公交线路从起点到终点的整个路段只有这一条线路,线路重复次数越多,重复度Ri的数值也相应提升,该值还可以作为公交线路之间相互影响的指标[9]。

(2)

其中,ni,b为从区域i到区域b的公交线路数量,nb,i为从区域b到区域i的公交线路数量,Ntotal为城市所有公交数量。

2.3 基于移动需求量的公交线路评价模型

假设乘客深夜利用公交出行时,一般离最近公交站的移动距离不会超过1 km。对应每个公交站的移动需求量是通过以该公交站的坐标为中心、半径为1 km的范围内,所有基站接收的数据量之和除于以该范围内的所有公交站数量(包括圆心处的公交站),具体指标为[10]:

(3)

其中,St=n为每个公交站的移动需求量,Dr=1为1 km范围内所有基站接收的数据量之和,Sn为1 km范围内所有公交站数量。

每个公交线路的移动需求量是通过上述方法获取的公交站移动需求量选取该路线经过的公交站进行整合后,除以该路线的公交站数量[11]。

(4)

其中,Lt=n为深夜公交线路的移动需求量,St=m为每个公交站的移动需求量,Sn为深夜公交线路上的公交站数量。

通过以上2个指标就可以综合地判断公交线路的合理性。St-n和Lt-n数据越大,说明该公交站和公交线的利用率很高,反过来,如果St-n和Lt-n数据很低,甚至达到0,则说明该公交站选址和公交路线的选线都存在问题,需要进行优化。

2.4 基于Dijkstra算法的公交线网优化模型

公交线路一般要求运输能力高,要注重提高效率。优化算法中通常考虑路径、通行量、换乘、道路、车辆、效益、政策等诸多因素[12]。由于本文研究的优化对象为深夜运营的公交线网,因此只考虑了线路通行量和路径长度2个因素,算法采用了Dijkstra模型。

G=(V,E,R,WT,WL)

(5)

其中,G为有向赋权图,V为网络上所有节点即公交站点的集合,E为有向图中所有边的集合,R为有向图中所有顶点的集合,WT为节点的非负权值集合,WL为节点的非负权值集合,表示在相应线路的线路长度权值。

在Dijkstra算法中,顶点集本文选取了地图中所有的道路交叉点和线路方向变化的转折点,以及根据前面分析模块中得到的移动需求量大的296个新增公交站点。边集则是根据百度地图中显示的实际路况而建立的拓扑关系。

3 实验结果与分析

3.1 深夜公交需求量现况分析

目前,上海深夜可利用的交通工具是公交和出租车2种。上海有39条深夜公交线路。平均运营时间及配车时间范围为11∶40—04∶10,经过的车站数量为800多个。线路平均行驶距离为20 km左右,最长线路的长度约为25 km,其中,21%的线路把火车站或者机场设为起始站和终点站。还有大部分的线路的出发点也都在这2个地点的附近。所以,可以看出深夜公交主要是充当着运送来往上海和其他城市之间人群的功能。为了更好地体现分析结果,本文把深夜移动需求量和既有深夜公交线路进行了叠加,并通过将信息放在地图上展现结果。

如图1所示,离市中心较远的A、B、D 3个区有非常大的深夜移动需求,但是却没有公交线路覆盖。既有的公交线路仅覆盖城市的核心地区。另外,C区虽然距离市中心只有10多公里,移动需求量也很大,但公交线路基本没有覆盖该地区。

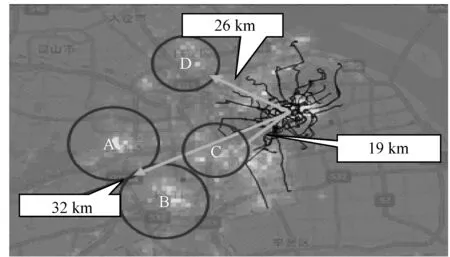
图1 上海深夜移动需求量和既有深夜公交线路

此外,本文研究还对深夜出租车的统计数据进行了分析,从图2可以看出,出租车的分布与移动需求之间也存在很大差异,有大量出租车移动数据量的区域公交线路分布不够。这从另一个方面也说明了优化设计公交线路的重要性和紧迫性。

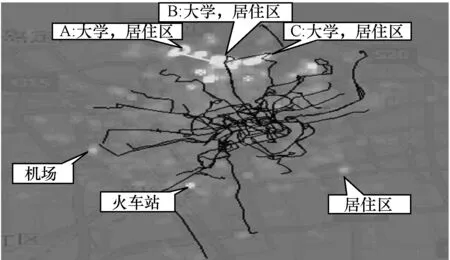
图2 上海深夜出租车移动数据和既有深夜公交线路

3.2 深夜公交区域分布现况分析

为了能够最大限度地进行均匀分配可用资源,本文研究将评价上海各区域内线路的重复度。

目前,深夜运营的公交线路所经过的行政区域数量共计12个(上海是分成17个行政区域),根据数据变化量,把该12个行政区域合并为7个研究区域,如图3所示,并对每个研究区域内的公交线路密度进行评价。

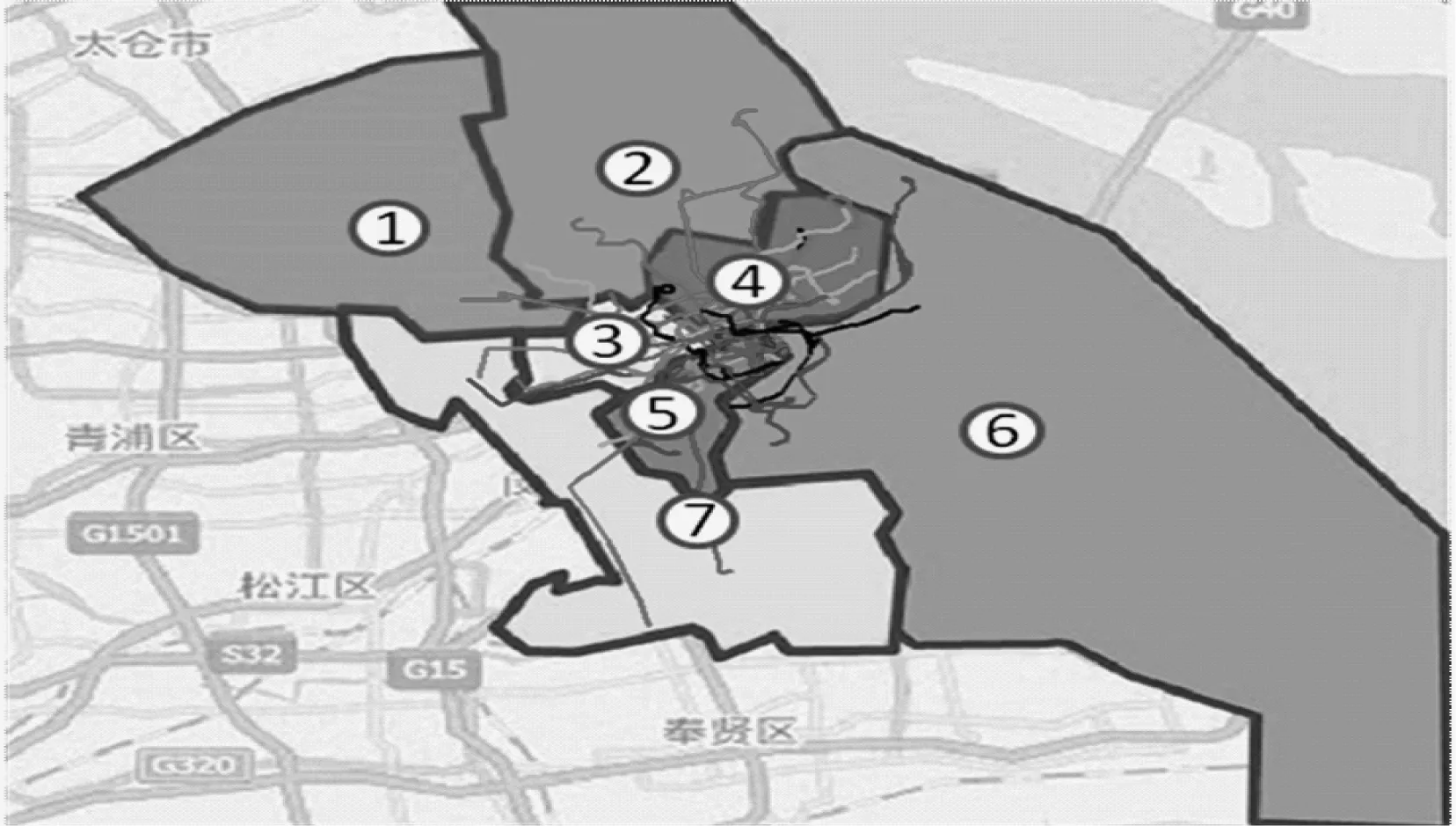
图3 上海深夜公交线路区域分布

根据表1所示结果显示,利用每个研究区域内的有移动需求的总量对该区域面积做平均,可以看到,该平均值在3、4、5这3个区域明显高于其他区域,这与现在的公交线路分布的密度是相互对应的。但是,从移动需求总量来看,区域6和区域1的移动需求量分别为43和50,很显然具有更大的移动需求。这表明线路的密度与移动需求存在不匹配的地方,而且相关公交线路能够连接的地区也不够。

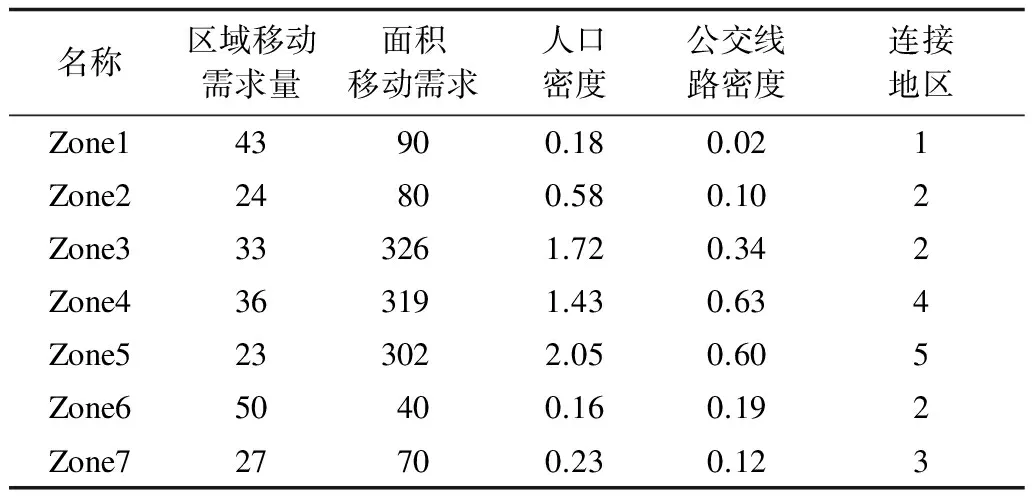
表1 研究区域公交线路密度评价结果

3.3 根据公交站移动需求量的公交线路评价

对各线路的车站周围的数据量进行分析,求出各车站及路线周边的数据变化量。对所有公交线路的公交站移动需求量进行了细致的分析。

以一个月的时间跨度,对全部39条公交的往返线路的每个公交站的移动需求量进行了统计,图4为该数据的分布。结果显示,799个公交站中大量的公交站的一个月的移动需求量并不大,其中,有42个站一个月内的总移动需求是0。只有少数线路有较大的需求量,很显然,说明公交站的设计总体上存在较大的问题。

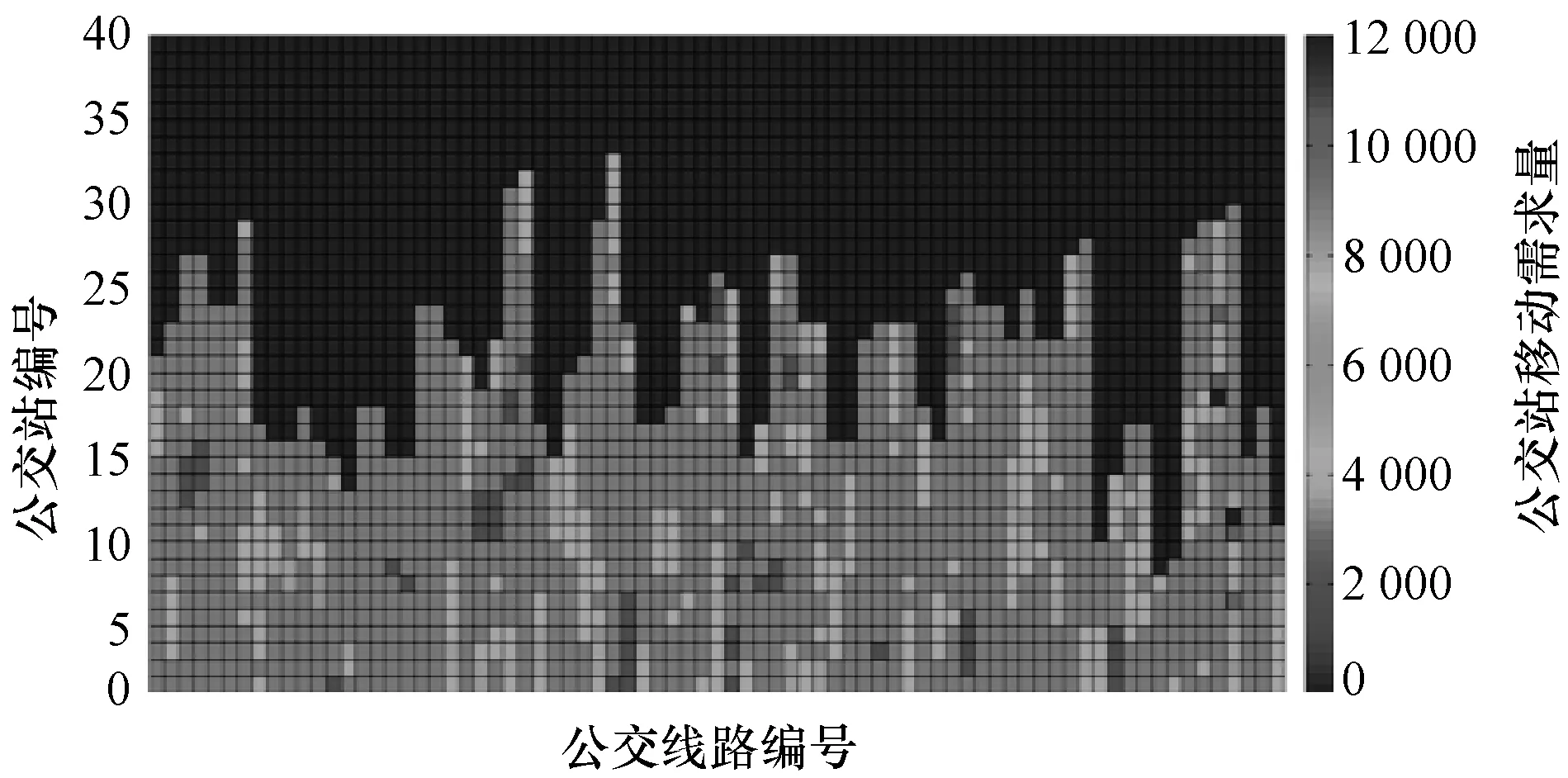
图4 各路线的公交站移动需求量

另外,还对39条公交的往返线路移动需求量进行了分析,如图5所示,很容易发现整个39条线路的移动需求量分布不均匀,显现出较大的非均衡性,甚至有些公交线路的移动需求量非常低。39条线路的移动需求量的均值为33 502,而方差达到了31 305,说明在公交线路的规划上存有较大的优化空间。

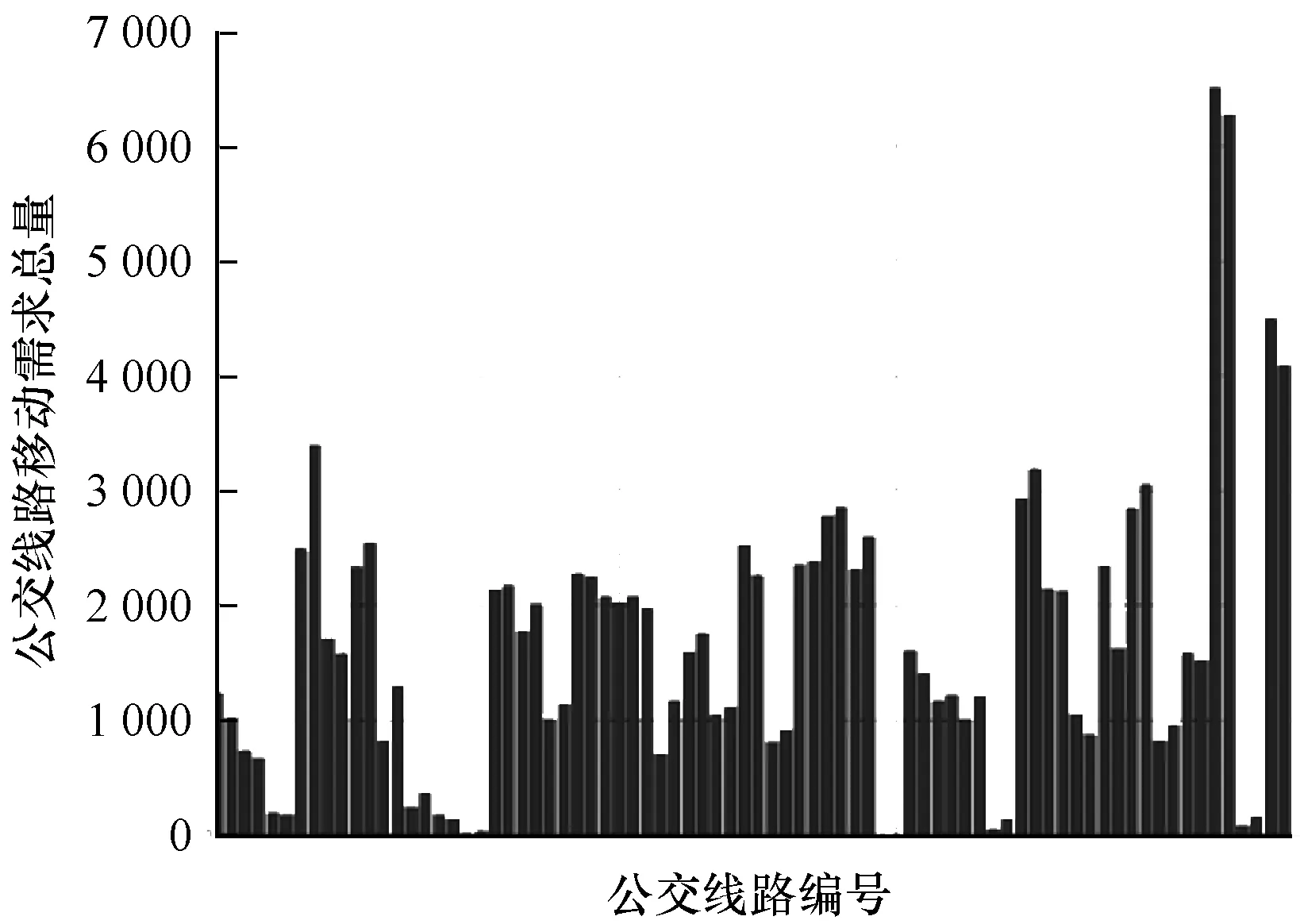
图5 各路线周边的公交站数据变化量

3.4 深夜公交线网及线路的设计

在优化公交线网时,为了能够最大限度地覆盖所有上海市深夜移动需求量高的站点,从所有站点中选取移动需求量最高的2 000个公交站点,其中包括既有站点和新增站点。另外,还考虑了出租车数据量高的地区,相应地调整了其中一部分公交站点。

考虑到公交线路需要覆盖城市大部分区域,即使有些区域相互之间移动需求量很低,也要把这些区域连接起来[13]。优化结果显示,新的深夜公交线网(见图6)基本覆盖了所有的深夜移动需求量和出租车移动数据量高的地方,而且新的公交线路(见图7)比起既有的深夜公交线路更能满足上海市深夜出行的需求。

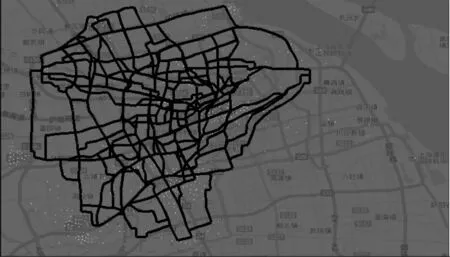
图6 新的深夜公交线网

图7 新的深夜公交线路

在Dijkstra模型中计算线路权重时,主要考虑了通行量和路径长度。为了让公交线路更多地覆盖移动需求量高的节点,在计算过程中,2个节点之间的权重不仅和它们之间的距离有关,而且和路径上的公交站移动需求量信息有关[14]。在利用Dijkstra模型时,不能直接处理节点带有权值的有向图的路径搜索,而需要将2个节点的移动需求量的总和按一定的比值融合到两点间的距离中,这样就能将该模型简化成最短路径算法[15]。

4 结束语

本文建立的评价模型为考虑区域均衡性的深夜公交线路评价模型,目的是为了达到整个深夜公交系统的均衡分布,确保深夜公交线网的覆盖程度。在评价过程中,选择整个城市的深夜公交线网为研究对象,根据上海主要移动网络供应商提供的移动数据,将上海12个行政区域分成7个研究区域,分析深夜公交线路的重复率与覆盖程度。该评价的重点主要放在深夜公交线路的分布上,具体路线选择及换乘等因素没有考虑。另外,在本次研究中引入了大数据,利用上海市移动供应商和出租车公司提供的乘客移动信息,经过筛选与整合之后,选用可视化工具对上海市深夜移动需求量分析结果进行了可视化显示,结果发现,与考虑区域均衡性的深夜公交线路评价结果有一些出入,说明了既有深夜公交线路的不合理性。

公交路线的分布状况与该区域的乘客及道路环境也有密切的关系。本文利用Dijkstra模型对既有深夜公交线路优化时,只考虑了2个公交站之间的移动需求量。因为公交属于大众交通工具,即使是人口稀少的区域也要实现与其他区域之间的交通连接。所以,要根据评价分析结果进行增加公交站点或延长公交路线时,需要进行相应的调整。本文研究评价及优化方法与去除既有不合理公交线路方法相比,更适合于增加公交线路的方案。

[1] HAN J H.BTRNDP investigation of the bus route network[J].Journal of the Korean Traffic Society,2005,23(8):19-29.

[2] OH J H.Big data visualization and visualization process[D].[S.1]:Korean Journal of Multimedia Institute,2014.

[3] YOO J U.The visualization of big data[D].[S.1.]:South Korea Consulting Association,2011.

[4] CH I M.Study on the location of a bus station considering bus routes[D].Philadelphia,USA:University of Pennsylvania,2007.

[5] HONG Z X.Research on route design[D].Gwangju,Korean:University of Kwangju,2006.

[6] 袁长伟,吴群琪,袁华智,等.考虑轨道交通作用效应的城市公交线网优化方法[J].公路交通科技,2014,31(8):119-125.

[7] 费 腾,张立毅,陈 雷.混合Levy变异与混沌变异的改进人工鱼群算法[J].计算机工程,2016,42(7):146-152,158.

[8] 冯正勇.衰落信道数据包传输跨层优化模型改进[J].计算机工程,2016,42(11):125-130.

[9] 蔡 彪,庹先国,桑 强,等.复杂网络中基于三角环吸引子的社区检测[J].计算机工程,2016,42(9):197-201.

[10] 沈记全,孔祥君.基于改进蚁群优化算法的QoS区间数服务组合方法[J].计算机工程,2016,42(7):181-188,193.

[11] 程宪宝.基于改进简化粒子群优化的多目标跟踪算法[J].计算机工程,2016,42(8):282-288.

[12] 杨兴地.中小城市常规公交线网优化方法研究[J].交通信息与安全,2013,31(5):55-61.

[13] 李淑庆.重庆市主城区公交线网优化标准研究[J].交通信息与安全,2010(5):43-45.

[14] 史苇杭,林 楠.一种联合的时序数据特征序列分类学习算法[J].计算机工程,2016,42(6):196-200,207.

[15] 郭羽含,杨晓翠.绿色供应链网络构建的双阶段综合优化方法[J].计算机工程,2016,42(10):192-200.