基于图覆盖的大数据全比较数据分配算法
高燕军,,,,2
(1.太原理工大学 信息工程学院,山西 晋中 030600;2.昆士兰科技大学 电机工程及计算机科学学院,澳大利亚 布里斯班4001)
0 概述
全比较是一类特殊的计算问题,广泛存在于生物信息学、生物测定学和数据挖掘等领域[1]。在生物信息学中,通过比较不同物种的基因序列对谱系关系进行推断[2]。在生物测定学的研究中,一个典型的全比较问题是通过对生物测定学数据库中的大量数据进行成对比较来识别人的生理特征的,如面部识别、指形判断、手掌扫描[3]。在数据挖掘中,相似矩阵的计算是分类和聚类分析中的一个关键步骤,它表示被考虑对象之间的相似度[4-5]。序列比对、聚类分析[6]以及当前的研究热点全局网络比对均属于计算生物学和生物信息学中典型的全比较计算问题[7]。
全比较计算代表了一种典型的计算模式,即数据集中的每个数据都要和该数据集中的其他所有的数据做一次比较计算[8-9]。当数据集中的文件个数或者文件所包含的数据变大时,全比较计算的规模随之变大[10]。当前,针对一些特定领域的全比较问题已有解决方法被提出,如著名的BLAST[11]和ClustalW[12]。然而,这些方法要求在系统中的每个节点上存储所有的数据文件,增加了时间开销和通信成本,而且需要巨大的存储空间。此外,分布式系统(如开源的分布式处理框架Hadoop[13])被广泛地用于解决大规模的数据密集型的计算问题,包括全比较计算[14]。然而,由于没有考虑比较任务和数据之间的依赖关系,基于Hadoop的数据分配策略对于全比较计算是低效的[15]。由此可以得出,数据分配的结果将直接影响全比较计算的整体性能。文献[10]将全比较计算的数据分配问题抽象为带约束条件的组合优化问题,并利用启发式算法求最优解。与Hadoop相比,该方法提高了整体的计算性能,但是随着数据量的增大,解空间变大,问题规模呈指数级增长[16]。此外,启发式算法也无法保证解的全局最优性[17]。
针对上述问题,本文提出基于图覆盖的数据分配算法(Data Allocation Algorithm Based on Graph Covering,DAABGC)。首先对全比较计算问题进行理论分析,将其归纳为图覆盖问题,然后构造最优图覆盖的解,根据特解设计相应的数据分配算法,以确保所有比较任务都包含本地数据,使节点之间达到负载均衡,从而在保证存储节约率的前提下,提高计算性能。
1 全比较与图覆盖
1.1 全比较计算
一个典型的全比较计算步骤如下:1)通过主节点管理和分配数据到各节点上;2)通过任务调度器生成计算任务,然后把任务分配到各节点上;3)各节点执行全比较计算,处理和任务相关的数据。各阶段示意图如图1所示。从中可以看出,数据分配和任务执行是大数据全比较计算的2个关键阶段。
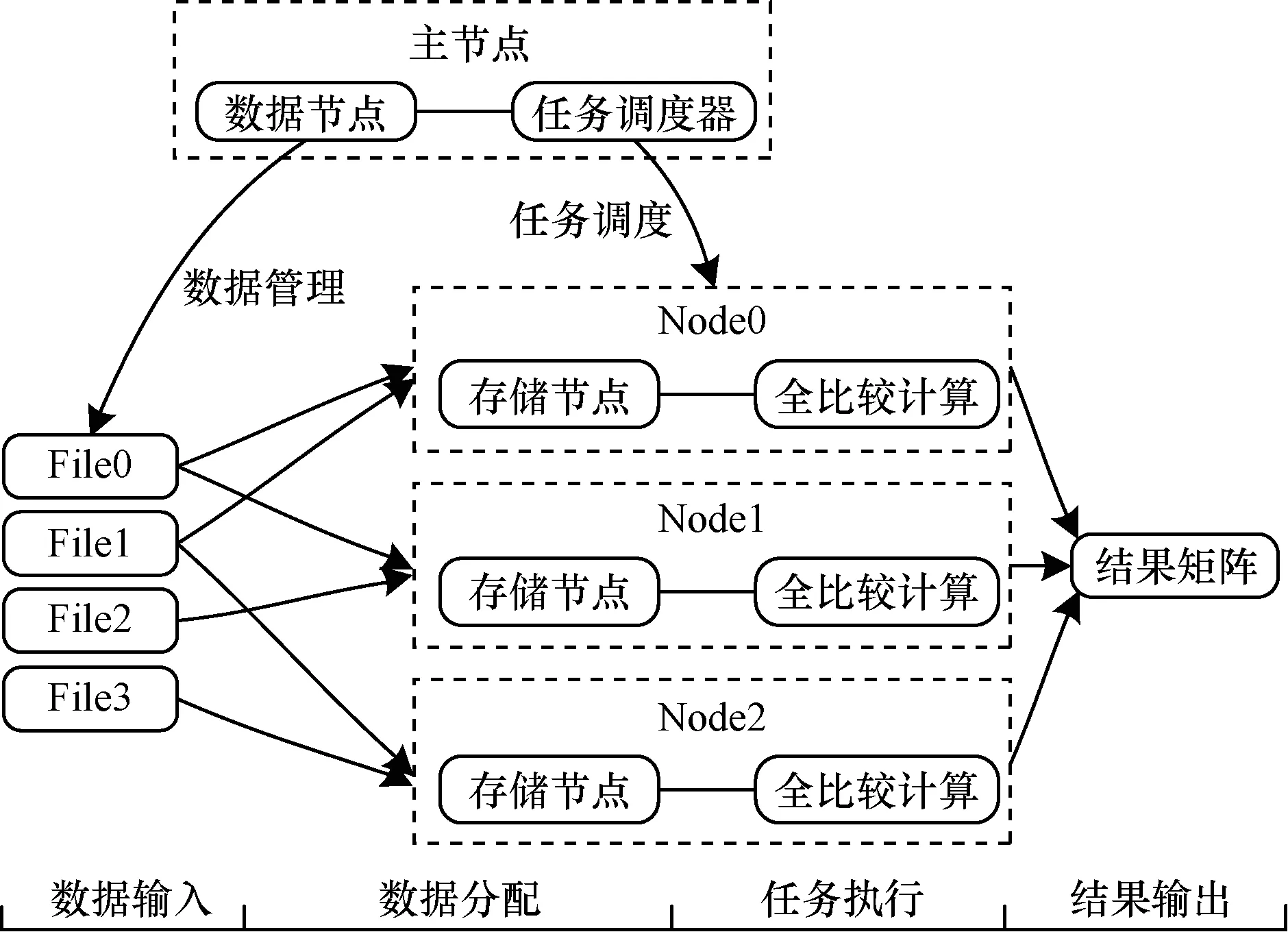
图1 大数据全比较计算各阶段示意图
为更高效地解决大数据全比较问题,首先提出2个假设:1)数据文件的大小相同或近似相同;2)比较任务的执行时间相同或近似相同。在真实的场景中,很多应用满足这2个特性,如协方差矩阵的计算、聚类分析中相似矩阵的计算等。本文研究的正是这类应用。其次,本文将从存储的使用和计算性能2个方面对该问题进行深入剖析。
1)减少存储使用
对于存储的使用,需要考虑2个问题:(1)每个节点的存储使用必须在其范围之内;(2)分配数据到各个节点上所花费的时间应该在可接受的程度之内。令|Di|为节点i上存储的文件数,则在考虑到上述2个条件的情况下,数据分配算法需要满足:
Minimize max{|D1|,|D2|,…,|Dk|}
(1)
最小化节点中最大的文件数可以使每个节点存储相似数量的文件并包含相似数量的可执行比较任务,原因是可执行任务的数量和节点上的文件数是成比例增长的。
2)提高计算性能
在全比较问题的分布式计算中,任务执行的总时间是由最后一个完成任务的节点决定的。为了完成每个比较任务,对应的节点必须访问和处理所需的数据。令K、tcom(k)和tacc(k)分别代表分配给最后一个完成任务的节点的任务数、任务k的计算时间和访问任务k所需数据的时间。那么,执行任务的总时间可以表示为:
(2)
为了减少式(2)中总的执行时间,数据分配算法需要满足2个条件:(1)任务分配均衡;(2)所有的比较任务都具有好的数据本地性。
令Ti为节点i执行的比较任务数,则对于N个节点、M个文件的全比较问题,共有M(M-1)/2个比较任务需要分配,那么任务分配均衡可以表示为:

(3)
好的数据本地性也可以公式化。如果一个比较任务所需的数据都存储在本地,那么该任务不需要通过网络来远程访问数据,因此,好的数据本地性意味着tacc(k)的最小值可以为0。令(x,y)、T、Ti、Di分别代表数据x和y之间的比较任务、所有比较任务的集合、由节点i执行的任务集合以及节点i上存储的数据集合,则好的数据本地性可以表示为:
∀(x,y)∈T,∃i∈{1,2,…,N}
x∈Di∧y∈Di∧(x,y)∈Ti
(4)
经上述讨论,将式(1)、式(3)、式(4)作为本文数据分配算法的优化目标。
1.2 图覆盖问题
1.2.1 图覆盖的基本概念
定义1完全图是每对顶点之间都恰好连有一条边的简单图,n个顶点的完全图有n(n-1)/2条边,记为Gn。
定义2假设G(V,E)代表一个图,其中,V表示顶点集合,E表示边集合。从集合V取若干个顶点组成集合V′,构成一个诱导子图,用G[V′]表示。
定义32个图G1(V1,E1)和G2(V2,E2)的联合为分别对顶点和边求并集,即G=(V1∪V2,E1∪E2)。如果存在n个诱导子图G(V1),G(V2),…,G(Vn)的联合G覆盖图G′,当且仅当G′的任何一条边存在于某个子图G(Vi)。
定义4给定一个图G=(V,E)和一个正整数k,把G划分为k个诱导子图G(V1),G(V2),…,G(Vk),如果满足2个条件:1)该k个子图的联合覆盖G;2)各子图中最大的顶点数最小,即minmax{|V1|,|V2|,…,|Vk|},其中|Vi|代表第i个子图中的顶点数,则称其为图覆盖问题。
定义5若某一个Gn的一些子图Gp、Gp之间无公共边,且Gn中的任意一边必定在某个Gp中,则称这些图Gp的联合为Gn的最优图覆盖,若不满足则称这些Gp不是Gn的最优图覆盖。
1.2.2 全比较问题到图覆盖问题的转化
把全比较计算映射为一个完全图,图中的顶点代表数据文件,边代表比较任务,如图2所示,其中,8个顶点代表8个数据文件,28条边代表28个比较任务,如C(3,8)、C(4,8)、C(4,7)分别表示3个不同的比较任务。因此,M个文件、N个节点全比较数据分配问题可以类比为把一个完全图GM划分为N个子图,且该N个子图的联合能够覆盖图GM。考虑到1.1节提出的优化目标,式(1)数据均衡意味着每个子图有相似数量的顶点,式(2)任务均衡意味着每个子图有相似数量的边,而式(3)数据本地性,按照最优图覆盖的子图划分方式,任意2个子图之间没有公共边,每个子图都自成一个完全图,所有的边都连着2个顶点,因此,可以确保比较任务具有100%的数据本地性。由此可以得出,全比较问题可以转化为最优图覆盖的求解问题。文献[18]证明最优图覆盖问题是NP完全问题。NP完全问题是非确定性问题,无法直接通过计算得到解,解决NP完全问题的一般方法是采用启发式算法。然而,随着M和N的增大,解的空间呈指数级增长。
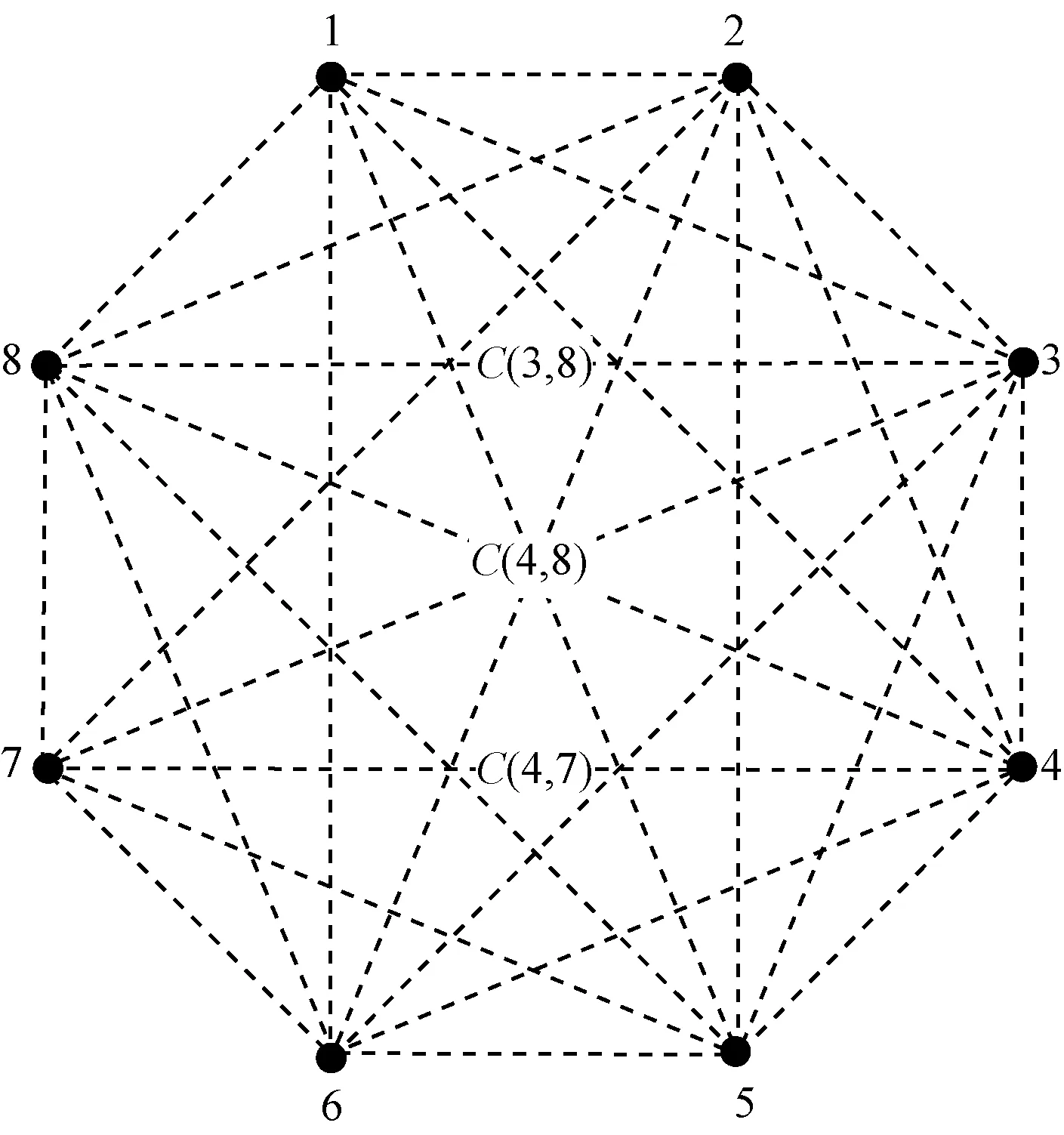
图2 8个文件的全比较计算示意图
通过研究可以发现,相同顶点数的子图Gp覆盖Gn的必要条件是n-1≥p(p-1)。
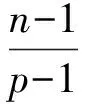
2 图覆盖最优解的构造方法
M=N=p(p-1)+1,p>2,其中M为文件数,N为节点数,当p=2,3时,问题相对简单,通过枚举法构造出最优解,如表1、表2所示,最优解可以表示为集合S={Ni(Vi1,Vi2,…,Vip)|i=1,2,…,n},其中n为节点数,Ni为节点i的编号,Vip为顶点p(即数据文件p)的编号。
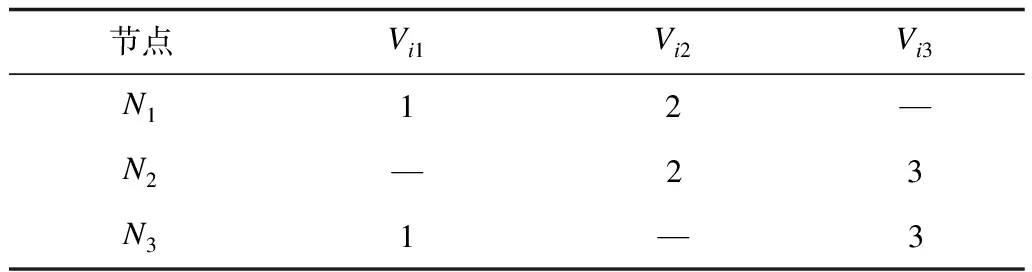
表1 p=2时图覆盖最优解
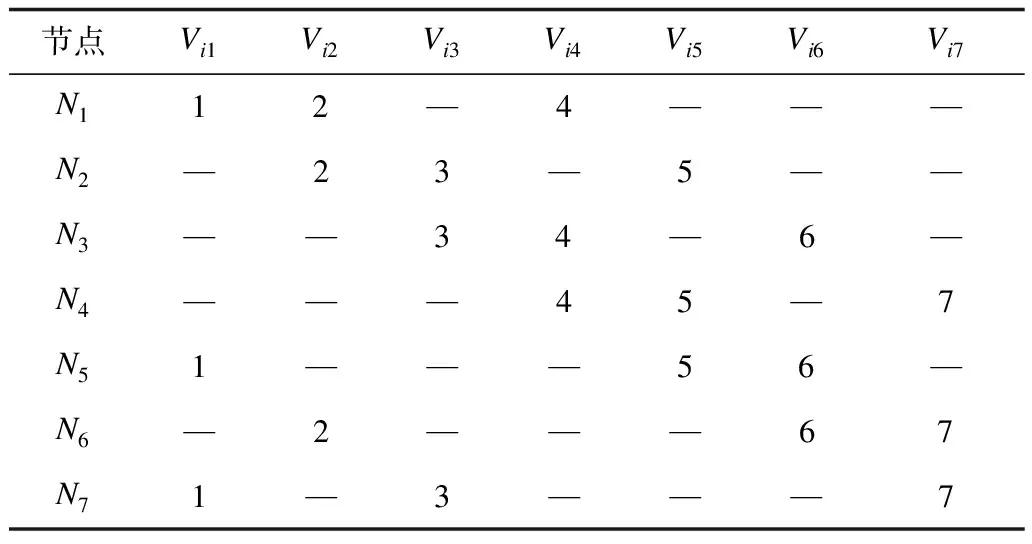
表2 p=3时图覆盖最优解
由表1、表2可以归纳出以下规律:
1)如果存在最优解,则每个节点上的文件个数为p。
2)相邻节点之间的解组合差1,如表2的N1(1,2,4),然后对组合中的各元素递增1,即为下一个节点上的顶点组合。当Vip递增为N+1时,将Vip置为1,然后对这p个点从小到大重新排列,继续递增,结果发现是一个循环。
3)在这p个点中,1和2是可以首先确定的2个点,在确定1和2的情况下,3是可以排除的,例如(1,2,3)递增1,则为(2,3,4),显然(2,3)为公共边,不满足最优图覆盖的条件。因此,第3个点从4开始。
4)由于这p个点是循环递增的,因此任意2个点之间的差值不能相同。如p=4,M=N=13,取4个点为(1,2,4,7),当递增到(4,5,7,10)时,将出现一条公共边,直到第4个数递增到13都会有公共边存在。
5)在满足规律1)和规律2)之后,在(Vi1,Vi2,…,Vip)的第p个点Vip递增到N+1之前都不会有公共边存在。当Vip=N+1时,将其置为1,此时,节点i上的解为(1,Vi2,Vi3,…,Vip),重新计算1和其他各点之间的差,且不能和之前的差相同。
3 数据分配算法
从第2节的分析中可以得到以下结论:
1)假设M=N=p(p-1)+1,p>2时存在图覆盖的最优解,则可以通过上文5条规律来构造该解。
2)在构造出最优解之后,数据和任务的分配可以根据最优解来进行。
3)由于之前所讨论的构造特殊解的前提是M=N,因此本文讨论M>N的情况。当M>N时,可以将文件均匀分成N个Block,每个Block中的文件个数差别不大于1,然后按照M=N的情况来构造解,并进行相应的数据分配和任务调度。如表3所示,N=7,M=9时可以构造7个Block。
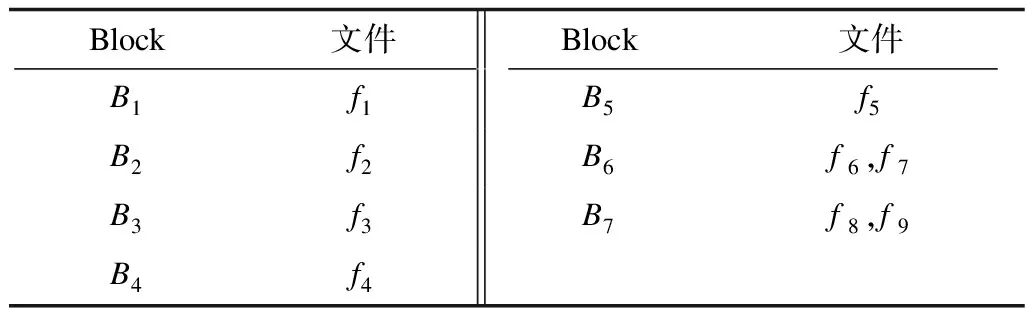
表3 N=7,M=9时Block的构造
根据上述内容,本文提出基于图覆盖的数据分配算法(DAABGC)。该算法分为2个步骤:
步骤1构造最优解。首先定义5个集合变量:L1用于存放已经找到的特解元素;L2存放特解中任意两点之间的差;L3存放L1和L2中元素的和;L4存放新找到的顶点和已有顶点的差;L5存放当Vi递增到N+1时,Vj,j=1,2,…,i-1和1的差,其中Vi表示第i个顶点,然后进行特解的构造。
步骤2分配数据和调度任务。当M=N时,根据步骤1得到特解进行数据分配;当M>N时,将数据文件均匀打包为N个Block,然后根据特解进行数据分配。
通过DAABGC算法,构造出当M=N=13,21,31时的最优解,加上手动构造p=2,3时的解,M=N=3,7,13,21,31时的特解如表4所示。

表4 M=N=3,7,13,21,31时的特解
DAABGC算法描述如下:
//构造最优解
定义变量:L1、L2、L3、L4、L5为5个集合变量
构造最优解S中组合N1(V1,V2,…,Vp)
V1=1,V2=2,V3从4开始
把V1、V2、V3存到L1,把V1、V2、V3之间任意2个元素之间的差无重复地存到L2
while V3 for i=4 to p do for x in L1do for y in L2do 把x+y无重复地放入L3 end for end for 对L3进行升序排序,在L3中搜索第一个在Vi-1和L3[last]之间没有的自然数,如果存在将其赋给Vi,否则把L3[last]++赋给Vi while Vi for z in L1do L4.add(Vi-z); end for 计算当Vi递增到N+1时,Vj,j=1,2…,i-1和1的差,并放入L5 if L2或L4包含的L5任意一个元素then Vi++; if Vi是Vi-1和L3[last]之间某个元素then L3[last]赋给Vi Continue end if else 把Vi放入L1,把L4,L5的元素拷贝到L2,清空L4、L5 break; end if end while if最优解的所有元素Vi全部找到then 保存最优解,并退出循环 else V3++; end for end while //根据最优解分配数据和任务调度 当M=N时,按特解来分配数据;当M>N时,将文件均匀地打包为N个Block,然后按照特解分配数据,最后根据数据分配的结果来调度任务 本节将通过实验来验证算法的有效性。首先介绍评价指标,然后根据每个指标依次对算法进行评估。 本文提出了4个评价指标来评估算法,分别为存储节约率、数据本地性、计算性能和可扩展性。 1)存储节约率。存储节约率是数据分配算法的目标之一,反映了算法对硬盘的节约情况,可有效度量存储效率。 2)数据本地性。数据本地性能够反映数据分配算法和计算性能的好坏。因为在本文的算法中,任务的分配是基于数据分配的结果,所以具有数据本地性的任务在数据分配完成之后可以统计出来。 3)计算性能。相对于存储节约率和数据本地性,计算性能能够更加直观地反映算法的性能。 4)可扩展性。可扩展性对于大数据全比较问题的大规模分布式计算是非常重要的。本文将对分布式系统中节点上不同数量的处理进行测试。 存储节约率的计算以每个节点上存储所有数据文件作为基准,以节点上的最大文件数Vmax为衡量标准,即max{|V1|,|V2|,…,|VN|}。存储节约率的计算式如下: (5) 在最理想的数据分配和任务调度情况下,Vmax存在理论下界。令M为文件数,N为节点数,则共有M(M-1)/2个比较任务,每个节点分配的比较任务不超过下式: (6) 为了完成比较任务所需的最少的文件,由于每个任务对应2个不同的数据文件,因此可以得到式(7)。 (7) 对式(7)进行计算得到: (8) 令M=256,对DAABGC算法和Hadoop进行对比。如表5所示,与在每个节点上存储所有的数据文件相比,DAABGC算法和Hadoop都具有很高的存储节约率,其中,Hadoop更高一些。当节点数为31时,DAABGC算法的存储节约率达到了80%,而Hadoop则为90%。虽然DAABGC的存储节约率相对较低,但是对于所有的比较任务,数据本地性都为100%,而Hadoop的高存储节约率是以牺牲数据本地性为代价的。例如,当节点数为31时,Hadoop的数据本地性只有14%。数据本地性对于大规模的全比较计算问题十分重要,好的数据本地性能够极大地减少任务执行时节点间的数据移动,因此,DAABGC算法在高存储节约率的情况下,数据本地性更好。 表5 不同数据分配策略的对比 计算性能由全比较问题总的执行时间来表征。下文对Hadoop和DAABGC算法进行比较。实验的设计如下: 1)实验的软硬件环境。如表6所示,为了测试算法在真实的集群环境下的性能,笔者搭建了Hadoop集群,操作系统采用Centos7,将其中一个管理节点作为主节点,另外一个管理节点作为主节点的备用节点,其他节点作为数据节点。主节点和备用节点,以及数据节点之间通过2个交换机冗余连接。 表6 集群的硬件配置 2)实验应用。作为生物信息学中典型的全比较问题,CVTree被选为测试计算性能的应用。CVTree在单机平台的计算已经实现[19],本文将在分布式的环境下来测试CVTree。 3)实验数据。本文选择国家技术生物中心的一组dsDNA文件作为实验数据,其中,每个文件的大小约为150 MB,总的数据量为20 GB。 本文对节点数为7时不同的数据文件做了测试。如图3所示,当M分别为93、109、124时,DAABGC的总运行时间都低于Hadoop,说明DAABGC算法对于解决CVTree来说具有更好的性能。 图3 2种算法的计算效率对比 为了更好地验证DAABGC算法的性能,对不同数量的文件,在节点数为7的情况下计算总的运行时间。如图4所示,对于相同的文件个数M,每个节点的运行时间是非常相似的,很好地满足了式(3)所表达的负载均衡。每个节点上的比较任务在执行时都访问了本地数据,因为节点之间不存在数据移动。 图4 7个节点的任务均衡性 可扩展性对于大数据集全比较问题的处理很重要。可扩展性的评估指标为加速比。 如图5所示,实验对处理器个数从1~7的情况进行测试。从中可知DAABGC算法获得了约6.335/7=90.5%的理想性能,由此可得,和Hadoop相比,DAABGC算法虽然占用了更多的存储空间,但是也获得了更好的性能,随着处理器数量的增加,获得了较好的加速比,因此,DAABGC算法具有良好的可扩展性,能够适应大数据全比较问题的大规模分布式计算的要求。 图5 本文算法获得的加速比 本文从存储使用和计算性能2个方面探讨如何高效解决大数据全比较问题,并基于图覆盖理论提出DAABGC算法。实验结果表明,该算法可构造出最优解,得到比Hadoop更好的性能。下一步将深入研究图覆盖问题最优解产生的理论依据,并针对更多领域的大数据全比较问题对DAABGC算法进行实验验证。 [1] ZHANG Y F,TIAN Y C,KELLY W,et al.Application of simulated annealing to data distribution for all-to-all comparison problems in homogeneous systems[C]//Proceedings of ICONIP’15.Berlin,Germany:Springer,2015:683-691. [2] HAO B,QI J,WANG B.Prokaryotic phylogeny based on complete genomes without sequence alignment[J].Modern Physics Letters B,2011,17(3):91-94. [3] PHILLIPS P J,FLYNN P J,SCRUGGS T,et al.Overview of the face recognition grand challenge[C]//Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Washington D.C.,USA:IEEE Computer Society,2005:947-954. [4] SKABAR A,ABDALGADER K.Clustering sentence-level text using a novel fuzzy relational clustering algorithm[J].IEEE Transactions on Knowledge and Data Engineering,2013,25(1):62-75. [5] 丁三军,薛 宇,王朝霞,等.基于模糊数据挖掘的虚拟环境主机故障预测[J].计算机工程,2015,41(11):202-206. [6] WONG A K,LEE E S.Aligning and clustering patterns to reveal the protein functionality of sequences[J].IEEE/ACM Transactions on Computational Biology and Bioinformatics,2014,11(3):548-560. [7] FAISAL F E,ZHAO H,MILENKOVIC T,et al.Global network alignment in the context of aging[J].IEEE/ACM Transations on Computational Biology and Bioinformatics,2015,12(1):40-52. [8] KRISHNAJITH A P D,KELLY W,HAYWARD R,et al.Managing memory and reducing I/O cost for correlation matrix calculation in bioinformatics[C]//Proceedings of IEEE Symposium on Computational Intelligence in Bioinfor-matics and Computational Biology.Washington D.C.,USA:IEEE Press,2013:36-43. [9] ANATHTHA P D K,KELLY W,TIAN Y C.Optimizing I/O cost and managing memory for composition vector method based on correlation matrix calculation in bioinformatics[J].Current Bioinformatics,2014,9(3):234-245. [10] ZHANG Y F,TIAN Y C,KELLY W,et al.A distributed com-puting framework for all-to-all comparison problems[C]//Proceedings of IECON’14.Washington D.C.,USA:IEEE Press,2014:2499-2505. [11] ALTSCHUL S F,GISH W,MILLER W,et al.Basic local alignment search tool[J].Journal of Molecular Biology,1990,215(3):403-410. [12] THOMPSON J D,GIBSON T J,HIGGINS D G.Multiple sequence alignment using ClustalW and ClustalX[EB/J].Current Protocols in Bioinformatics,2002,2(3). [13] 栾亚建,黄翀民,龚高晟,等.Hadoop平台的性能优化研究[J].计算机工程,2010,36(14):262-263. [14] CHEN Q,WANG L,SHANG Z.MRGIS:a MapReduce-enabled high performance workflow system for GIS[C]//Proceedings of the 4th IEEE International Conference on e-science.Washington D.C.,USA:IEEE Computer Society,2008:646-651. [15] 程 苗,陈华平.基于Hadoop的Web日志挖掘[J].计算机工程,2011,37(11):37-39. [16] GILLETT B E,MILLER L R.A heuristic algorithm for the vehicle-dispatch problem[J].Operations Research,1974,22(2):340-349. [17] LIN S,KERNIGHAN B W.An effective heuristic algorithm for the TSP[J].Operations Research,1973,21(2):498-516. [18] THITE S.On covering a graph optimally with induced subgraphs[J].Computing,2006,44(1):1-6. [19] KRISHNAJITH A P D,KELLY W,HAYWARD R,et al.Managing memory and reducing I/O cost for correlation matrix calculation in bioinformatics[C]//Proceedings of IEEE Symposium on Computational Intelligence in Bioinformatics and Computational Biology.Washington D.C.,USA:IEEE Press,2013:36-43.4 实验
4.1 评价指标
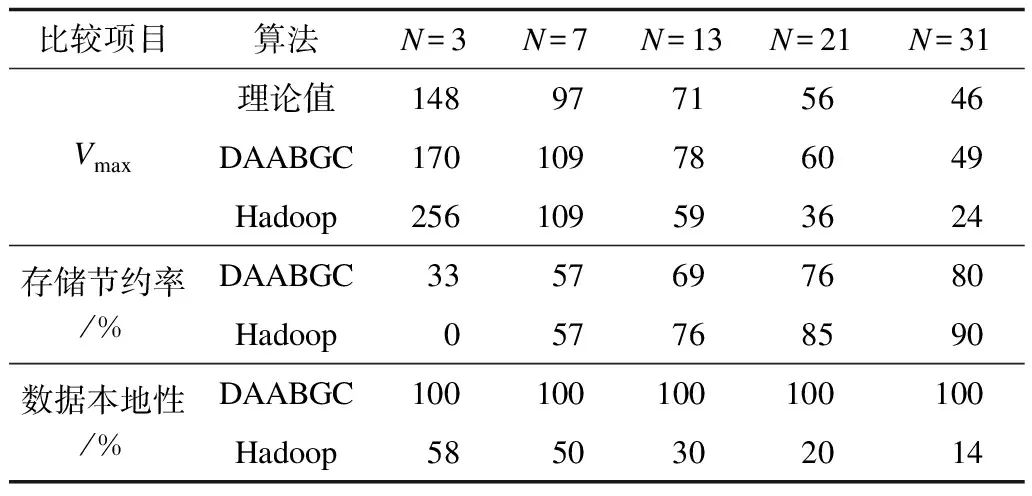
4.2 存储节约率和数据本地性

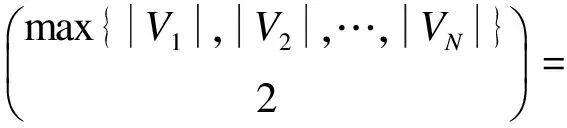
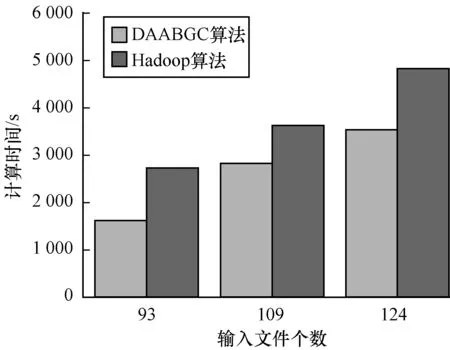
4.3 计算性能


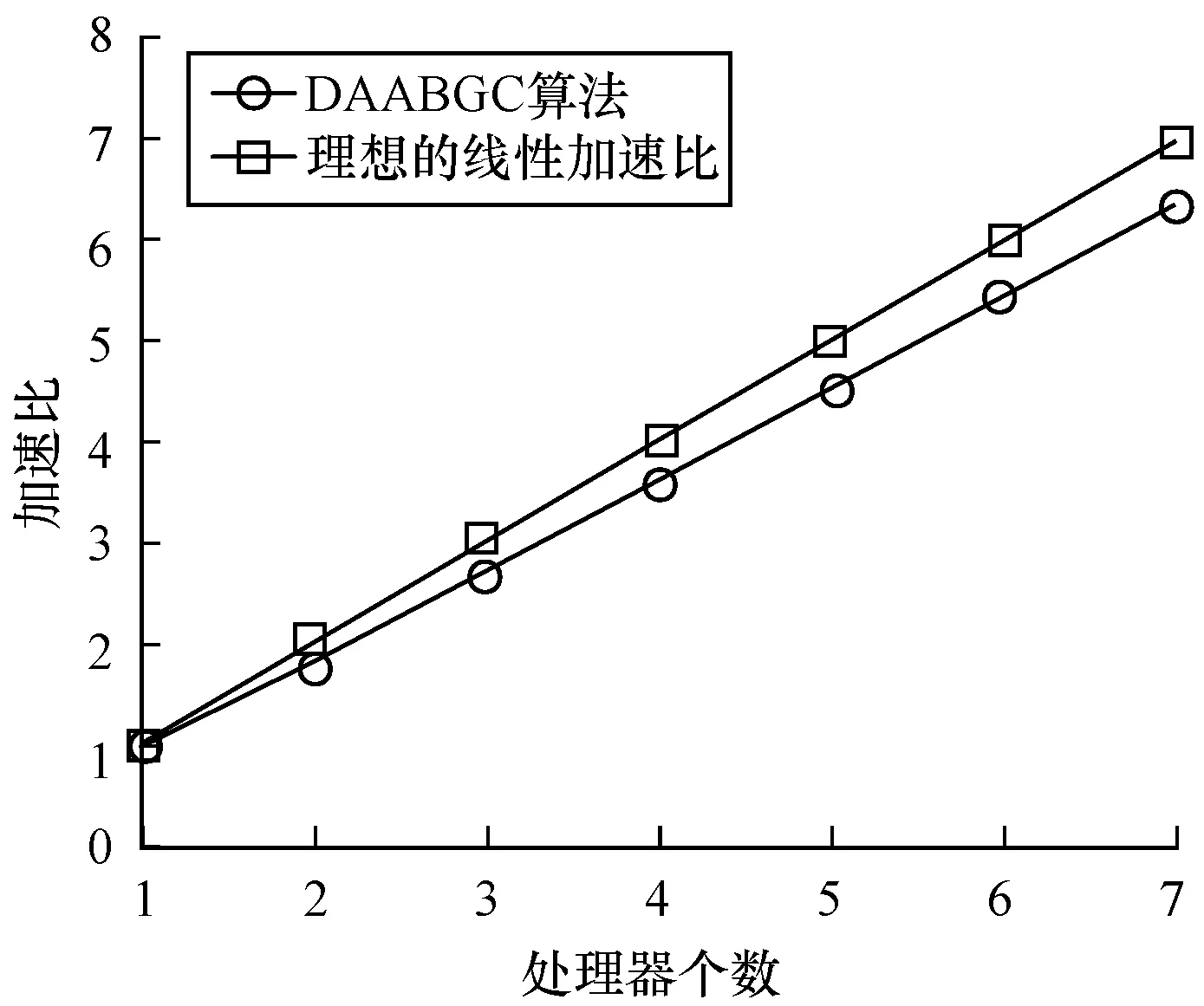
4.4 可扩展性
5 结束语

