余弦度量的多流形最大间距鉴别保持嵌入

林克正,王海燕,林璇玑,李 骜

(哈尔滨理工大学 计算机科学与技术学院,哈尔滨 150080) E-mail:wanghaiyan45@yeah.net

1 引 言

目前,基于统计学习的算法是人脸识别中被广泛应用的方法,比较有代表性的算法如主成分分析[1](Principal Component Analysis,PCA)和线性鉴别分析[2](Linear Discriminant Analysis,LDA),这两种方法都是线性方法,后来衍生出了对应的非线性方法,通过融入核方法,提出了对应的核主成分分析[3]( Kernel Principal Component Analysis,KPCA)算法和核鉴别分析[4](Kernel Discriminant Analysis,KDA)算法.随着“流形”概念的提出,基于流形学习的人脸特征提取方法得到越来越多的青睐,随之而来也出现了很多流形学习算法.其中,等距映射算法[5](Isometric Mapping,ISOMAP)和局部线性嵌入算法[6](Locally Linear Embedding,LLE)和拉普拉斯特征映射[7](Laplacian Eigenmap,LE),是比较经典的流形学习算法.基于流形学习的人脸识别方法都是以最大程度保持样本降维后的本质特征和原始空间拓扑结构为目标.上面的流形学习方法对新样本数据没有定义,泛化能力不强.针对这个问题,有人提出了局部保持投影算法[8]( Locality Preserving Projections,LPP),该方法和LE原理相似,通过对样本构建邻接图,来描述样本的邻域关系和相似度情况,虽然在一定程度上反映了样本的局部结构和样本总体布局,但是对正确分类并没有起到最直接的促进结果.通过加入样本类别信息进行构图,有人提出了边界费舍尔分析[9](Margin Fisher Analysis,MFA).MFA通过构造内蕴图和惩罚图有效地区分了不同类样本的边界,然而MFA也存在小样本的奇异值问题等.为了进一步保持样本的邻域结构,同时对同一邻域范围内的不同类样本进行区分,Huang等人提出了LMMDE(Local Maximal Margin Discriminant Embedding,LMMDE)算法[10],LMMDE算法既利用了样本类间邻域结构也利用了类内邻域结构信息,同时保持了样本的局部结构特征,相比于MFA算法,识别率有所提升.然而上述提出的几种流形学习方法面临以下的问题:

1) MFA和LMMDE算法均需要构造邻接图(MFA需要构造两类图,需要两个近邻参数k1和k2;LMMDE需要一个近邻参数k),近邻参数k的选取不当会对识别率造成影响;

2) 在实际的人脸识别工作中,可供选择的样本数量较少,在少样本情况下的各算法的识别率还有待于提高.鉴于以上问题,在LMMDE算法原理基础上,引入余弦距离和多流形[11]的思想,提出了余弦度量的多流形最大间距鉴别保持嵌入(Multi-manifold Maximal Margin Discriminant Preserving Embedding based on Cosine Measure).该算法中,首先对样本分块,为单个样本构造流形,整个训练样本集就构成多流形;然后在确定多流形中各个样本的邻域时,采用余弦距离的度量方式替换传统的欧式距离;最后重新定义计算测试样本和训练样本的流形间距离来对样本进行分类.由于CMMMMDPE方法采用余弦距离的度量方式,不仅避免了近邻参数k的选择困难问题,同时使得算法对离群数据更为鲁棒.多流形思想的融入,不仅解决了小样本问题,还能充分利用样本内部结构信息,进而提高识别率.

2 局部最大边界鉴别嵌入

LMMDE算法的中心思想:保持降维后的样本在原始高维空间中的邻域结构关系,同时最大化同一邻域内的不同类别样本的间隔,最小化同类样本的间隔,以达到对同一流形内的不同类样本进行分离的目的.设高维空间中样本集合为:X={x1,x2…,xN}∈RD,LMMDE的目标就是找到最优投影矩阵A,实现样本数据从高维空间到低维空间的映射:X→Y∈Rd.首先对每个样本点构造k近邻图,得到若干个邻接图.任意样本xi的邻域Nk(xi)表示由xi的前k个欧式距离最近的点构成的集合.

样本的局部散布矩阵,描述了样本的局部邻域关系,可按以下公式进行计算:

(1)

样本的类间邻域散布矩阵和类内邻域散布矩阵分别按照以下公式计算:

(2)

(3)

(4)

(5)

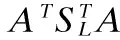
(6)

其中,A是投影矩阵,I是一个单位矩阵.

3 CMMMMDPE算法

3.1 余弦距离

图嵌入的算法在进行权值矩阵的定义时,反映了样本之间相似程度的权值通常采用热核函数法,由热核函数法的原理可知,两个样本之间的欧式距离大小决定了样本之间的相似度,即:欧氏距离越小,样本相似度越大;反之,样本相似度越小.在对一些离群孤立样本点确定近邻时,欧氏距离并不能准确地描述这个孤立样本点与其他样本点的关系,尤其在分类时极有可能做出错误判定.一些文献表明,余弦距离在面对离群孤立点则表现出了更加鲁棒的性能[12].首先引入样本间的余弦距离.令cos(xi,xj)表示样本xi与xj间的余弦距离,则cos(xi,xj)的计算公式为:

(7)

3.2 多流形思想的构图方式

多流形思想的原理是:考虑对样本集构造一个多流形空间,即对每个样本进行分割,最后形成若干个局部小块样本,由于它们来自同一个样本,属于相同的类别,因此将这若干个局部小块样本看成一个流形空间.这样,一个样本就构成了一个流形空间,整个样本集就构成多流形空间.CMMMMDPE算法就是基于这样的原理,首先对样本空间进行重新构造,构造一个多流形的样本空间,之后进行相应的构图、权值的赋值、目标函数的定义等步骤.

3.2.1 构造多流形空间

首先对原始样本数据构造多流形空间.对于一个含有N个样本图片数据集:I={I1,I2…,IN},它的向量形式表示成:X={x1,x2…,xN}xi∈RD.任意一个图像样本Ii(尺寸为p×q,这里p表示样本图片的高度,q表示样本图片的宽度).首先,对于一个样本点xi,将其分成l个块(l=1…t),这样形成多幅小块图片xil(尺寸为a×b,这里a表示样本图片的高度,b表示样本图片的宽度).l个小块图片样本构成一个流形空间.对于一个N个样本的数据集来说,可以构造多个流形空间,即M={M1,M2,…,MN},其中Mi=[xi1,xi2,…,xil].

3.2.2 邻域的确定

对于样本xil,在整个多流形空间中搜索满足余弦度量规则的小样本成为其近邻.样本xil的多流形类间邻域和多流形类内邻域通过以下两个公式来计算:

(8)

(9)

上面两个式子中这种采用余弦距离的度量方式确定近邻的方法,对于受到局部噪声干扰而离群的小样本来说,依然能找到正确的近邻.xil的多流形类间近邻反映了小块样本xil与多流形空间中不同类别的若干个小样本的邻接关系;xil的多流形类内近邻则体现了xil与多流形空间中同类的小样本的近邻情况.

3.2.3 权值的赋值

在确定了各个小块样本xil的类间邻域和类内邻域后,还需要构造权值矩阵来描述样本的相似度情况.多流形中每个小样本xil与多流形类间邻域内各样本的相似度权值定义如下:

(10)

多流形中每个小样本xil与多流形类内邻域的各样本的相似度权值定义如下:

(11)

3.3 多流形类间邻域离散度、类内离散度和总体样本局部散度

(12)

(13)

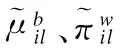
整个多流形样本空间中,对任意样本xil的局部邻域内的样本之间的相似度度量定义如下:

(14)

因此,局部离散度定义如下:

(15)

3.4 目标函数及最优投影矢量

基于余弦距离的多流形最大间距鉴别保持嵌入的思想就是:

1) 在低维嵌入空间中,保持多流形空间中小样本在原始高维多流形空间中的局部特征和空间散布关系;

2) 充分利用多流形空间中每个小样本的几何结构信息,最大化不同类别样本的多流形类间离散度与同类样本的多流形类内离散度的差值,使流形间的类别可分性最大,多流形的同类样本结构更加紧凑、多流形的不同类样本更加分离.算法的目标函数可表述为:

(16)

其中,Jb(A1,A2,…,AN)、Jw(A1,A2,…,AN)、JL(A1,A2,…,AN)的计算公式如下:

(17)

(18)

(19)

其中β是平衡因子,用来平衡目标函数中各项的重要程度,将(17)、(18)、(19)带代入目标函数(16)改写为:

(20)

对变换矩阵A=[A1,A2,…,AN]进行求解,需要求解出每个流形的降维矩阵Ai,Ai可通过最大化下面的公式进行求解:

max{(1-β)(Jb(Ai)-Jw(Ai))-βJL(Ai)}=max{(1-β)

(21)

Jb(Ai)、Jw(Ai)、JL(Ai)公式可按照以下过程进行化简:

(22)

(23)

(24)

其中,

(25)

(26)

(27)

Ai可通过以下公式的特征值分解问题得到:

[(1-β)(Hb-Hw)-βHL]Ai=λAi

(28)

3.5 模式识别与分类

按照CMMMMDPE算法进行降维后,每个样本流形都得到对应的投影矩阵Ai,i=1,2,…,N,利用最近邻分类器进行分类,分类过程如下:

Step1.对于给定的测试样本xT和训练样本集中的所有样本均按照本文算法进行特征提取,得到其在低维空间的表示MyT={yT1,yT2,…,yTt}和Myi={yi1,yi2,…,yit}.

Step2.计算多流形下测试样本MyT与训练样本Myi的距离.对流形MyT中的每个局部小块样本yTl,用余弦距离来度量Myi中哪些局部小块样本可以成为yTl的近邻点,得到的近邻点集表示为Ni(yTl),计算公式如(29)所示.

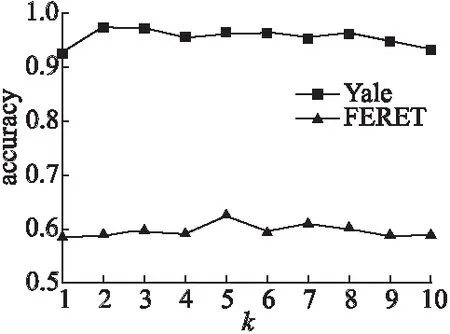
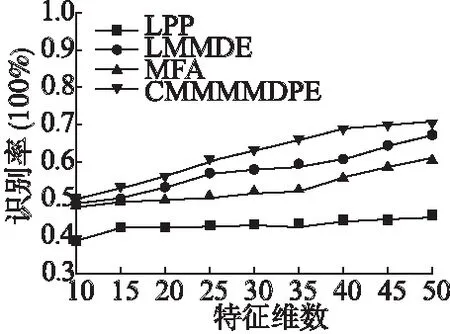
Ni(yTl)={yir,cos(yTl,yir)

(29)

yTl到低维流形yi的距离计算公式为:

(30)

则yT到流形yi的距离可按照如下公式计算:

(31)

Step3.识别分类.按照上面步骤求出测试样本到N个样本流形的距离.根据最近邻分类器原则,将测试样本yT的类别判定为d(yT,yi)值最小的对应yi的类别属性,判定公式如下:

(32)

4 实验结果与分析

在本节的实验主要是在ORL、Yale和FERET人脸库上进行,通过加入对比算法LPP、MFA、LMMDE,验证CMMMMDPE算法的有效性.实验的目的主要有以下几点:

1) 各种参数对算法的识别率影响;

2) 考查不同特征维数下的各算法识别率情况;

3) 测试样本数量对CMMMMDPE及其对比算法的识别率的关系.

ORL人脸库由400幅图像组成.采集了40名受试者每人10幅图像,这些图像分别采集于不同时间并包含了各方面变化如:不同视角、不同光照、不同表情、不同面部装饰物等情况.Yale人脸库共包含了165张图片,来自于15名受试者,每人有11张图片.每个受试者的人脸图片的主要差异在表情的变化及有无眼镜装饰光照情况的差别等.FERET人脸图片库的规模很大,包含了1199个人将近14000多幅图像,均是在不同拍摄角度、姿态和不同面部表情下采集的.在本节实验中,选取ORL和Yale人脸库中的所有图片;对于FERET人脸数据库,则选用它的一个子集共包含了200×7幅图像(由200人组成,每人有7幅图片).图1、图2和图3分别展示了Yale和FERET人脸图片库上某个人的人脸图像.

图1 ORL人脸数据库某个人的几幅人脸照片Fig.1 Several images of certain person on ORL face database

图2 Yale人脸图片库某个人的人脸图像Fig.2 Face images of certain person on Yale face database

图3 FERET人脸库上某个人的人脸图像Fig.3 Face images of certain person on FERET face database

实验中将图片进行裁切,只保留脸部区域,将图片统一处理成分辨率大小为32×32以保证实验结果的准确性.本节实验中涉及的Train(m)/Test(n)表示:实验数据集中,每个人脸的图片集中选取的训练样本数为m,测试样本数为n.

4.1 参数变化对识别率的影响

本实验中,因为CMMMMDPE算法是在LMMDE算法的基础上进行的改进,LMMDE算法在构图过程中需要确定近邻参数k,CMMMMDPE算法不需要指定近邻参数k,因此考察近邻参数k的不同取值对LMMDE算法的识别率影响.其次,考察权重参数β的不同取值对CMMMMDPE算法识别率的影响.两种实验均采用以下的实验数据:Yale人脸库中每人的人脸图片数量分配为:Train(5)/Test(6);FERFT人脸库中实验组中每个受试者的人脸图片分配情况:Train(4)/Test(3).图4展示了LMMDE方法的识别准确率对近邻参数k的敏感程度.此实验中先将β设为0.1,k的取值范围为k={1,2,…,10}.

图4 LMMDE算法在不同k取值下的识别率

从图4的实验结果可以看出,当近邻参数k从1变化到10时,LMMDE在Yale人脸库和FERET人脸库上的识别率具有较大的变化.其中,在Yale人脸库上LMMDE的识别正确率变化的最大幅度为5%左右,而在FERET人脸库上的识别率变化幅度约为3%.两个实验人脸库上的结果均表明LMMDE算法对于近邻参数的变化比较敏感,可见LMMDE算法对近邻参数k的依赖性较强.CMMMMDPE在确定样本近邻的过程中,通过比较两个样本之间的余弦角距离,来确定哪些样本可以成为近邻,不需要设置近邻参数k,较好地解决了近邻参数k选择不好所带来的识别率问题,从而验证了CMMMMDPE的有效性.

图5 CMMMMDPE算法在β取不同数值时的识别率

在进行参数β对算法识别率关系的实验中,β的取值范围为:β={0.1,0.2,…,0.9}.图5展示了CMMMMDPE算法识别率在不同人脸库上随权重参数β的变化情况.实验结果表明CMMMMDPE的识别率高低与权重参数β成反比的趋势,即:β越小,样本的鉴别信息对识别率更要重要,反之,样本局部结构特性对算法识别率的作用更大,β取值为0.1时,CMMMMDPE的识别率最佳.

4.2 识别率与特征维数实验

在Yale人脸库的实验组为:Train(5)/Test(6).在FERET人脸库的实验组为:Train(4)/Test(3).实验中涉及的参数设置如下:LPP和LMMDE算法的近邻参数k的范围是k={1,2,…,10};令l表示训练样本数,则MFA中的类内近邻参数kw=l-1;而类间近邻参数kb=C·kw,C表示样本的类别数.实验中涉及的权重参数β预先设为0.1;识别分类阶段均采用最近邻分类器,其中CMMMMDPE算法在模式分类时则采用本文的流形距离计算公式来进行分类.每个实验重复进行20次,取平均值.图6和图7展示了Yale和FERET人脸库实验上不同特征维数下各算法的识别率.

图6 Yale人脸库上的各算法在余弦距离分类器下的识别率Fig.6 Recognition rate of each algorithm by using cosine distance based classifier on Yale face database

图6和图7的实验结果表明,随着特征维数的增加,各算法的识别率是逐步增加的.利用样本类别信息的算法的识别率均高于LPP算法,LMMDE算法在保持样本的局部结构的同时还尽量区分开邻域内类别不同的样本,因此LMMDE的识别率均高于MFA.CMMMMDPE的识别率最高.然而在Yale人脸数据库上的实验结果表明,CMMMMDPE算法在特征维数达到一定数值以后,识别率甚至有所下降,这是因为当样本维数太高时,CMMMMDPE方法容易提取出非关键特征从而造成对识别分类的干扰,阻碍了正确分类过程.总的来说,本文算法CMMMMDPE由于加入多流形思想,使得每个流形空间中的小块样本充分发挥了样本内部结构信息的作用,同时引入的余弦距离度量方式对分类识别也起到较好的作用.

图7 FERET人脸库上的各算法在欧式距离分类器下的识别率Fig.7 Recognition rates of each algorithms by using euclidian distance based classifier on FERET face database

4.3 样本数对识别率的影响

本文算法由于加入了多流形思想,目的是为了解决样本数量较少时的识别分类问题,验证小样本下的识别率情况,因此本节实验主要在图片数量较少的ORL和Yale人脸库上进行.在ORL和Yale人脸库上的实验样本选择数据集上的所有图片.在ORL人脸库的实验组为:Train(5)/Test(5)、Train(4)/Test(6)、Train(3)/Test(7)、Train(2)/Test(8);在Yale人脸库上的实验组为:Train(5)/Test(6)、Train(4)/Test(7)、Train(3)/Test(8)、Train(2)/Test(9).表1和表2展示了不同人脸库中各算法在训练样本数量和测试样本数量取不同取值时的识别率情况.表中数据表明:随着训练集图片个数的增加,CMMMMDPE的识别率有小幅度提升并且一直高于其它算法,并且在样本数量较少的情况下CMMMMDPE的识别率效果显著优于其他对比算法,最佳识别率达到93.9%左右.对于CMMMMDPE算法来说,在小样本情况下(样本数为2或者3),相比于样本数量较多的情况下识别率只是略有下降,说明CMMMMDPE对小样本情况下能得到较多有用的分类信息.而与此形成对比的是其他算法则对训练样本的数量有显著的依赖.

表1 Yale人脸库不同训练样本数下的算法识别率
Table 1 Recognition rates of each algorithm with different number of train samples on Yale face database

训练样本数5/64/73/82/9LPP93.9±1.192.6±1.490.8±1.785.4±1.8MFA95.6±1.194.1±1.392.9±1.289.4±1.0LMMDE96.4±0.895.8±0.793.8±0.391.0±1.0CMMMMDPE98.2±0.697.4±0.696.5±0.695.2±0.6

表2 ORL人脸库不同训练样本数下的算法识别率
Table 2 Recognition rates of each algorithm with different number of train samples on ORL face database

训练样本数5/54/63/72/8LPP87.2±1.186.7±1.480.4±1.775.1±1.8MFA89.1±1.188.9±1.385.8±1.281.2±1.0LMMDE92.4±0.892.1±0.790.8±0.385.0±1.0CMMMMDPE93.9±0.693.4±0.692.5±0.690.2±0.6

5 结 语

本文提出一种基于余弦距离和多流形思想的CMMMMDPE算法,通过融入多流形思想和余弦距离度量方式解决了LMMDE算法中近邻参数k的选择困难问题和小样本识别率低问题.一方面,在确定样本的多流形类间近邻和多流形类内近邻,用余弦距离的度量方式避免了构图过程中对近邻参数k的选取,消除了近邻参数k对算法识别效果的影响;另一方面,通过多流形的理论为每个样本构造流形空间,充分保持了每个流形之间的内部局部结构信息,也从全局上保持了流形局部邻域关系,从而提高了小样本情况下的识别率.

[1] Turk M,Pentland A.Eigenfaces for recognition[J].Journal of Cognitive Neuroscience,1991,3(1):72-86.

[2] Belhumeur P N,Hespanha J P,Kriegman D J.Eigenfaces vs.Fisherfaces:recognition using class specific linear projection[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,1997,19(7):711-720.

[3] Scholkopf B,Smola A,Muller K R.Nonlinear component analysis as a kernel eigenvalue problem[J].Neural Computation,1998,10(6):1299-1319.

[4] Mika S,Rätsch G,Müller K R.A mathematical programming ap-

proach to the kernel fisher algorithm[C].Advances in Neural Information Processing Systems,2001,13:591-597.

[5] Tenenbaum J B,De Silva V,Langford J C.A global geometric framework for nonlinear dimensionality reduction [J].Science,2000,290(5500):2319-2323.

[6] Roweis S T,Saul L K.Nonlinear dimensionality reduction by locally linear embedding [J].Science,2000,290(5500):2323-2326.

[7] Belkin M,Niyogi P.Laplacian eigenmaps and spectral techniques for embedding and clustering[J].Advances in Neural Information Processing Systems,2002,14(6):585-591.

[8] He Xiao-fei,Yan Shui-cheng,Hu Yu-xiao,et al.Face recognition using laplacianfaces[J].IEEE Trans on Pattern Analysis and Machine Intelligence,2005,27(3):328-340.

[9] Yan S,Xu D,Zhang B,et al．Graph embedding and extensions:a general framework for dimensionality reduction[J]． IEEE Trans Pattern Anal and Mach Intelligence,2007,29(1):40-51.

[10] Huang P,Tang Z,Chen C,et al.Local maximal margin discriminant embedding for face recognition[J].Journal of Visual Communication & Image Representation,2013,25(2):296-305.

[11] Yang Zhang-jing,Wan Ming-hua,Wang Qiao-li,et al.Multi-manifold unsupervised linear differential projection algorithm[J].Journal of Frontiers of Computer Science and Technology,2016,10(11):1576-1586.

[12] Huang Pu,Tang Zhen-min.Parameter-free locality preserving projections and face recognition[J].Pattern Recognition and Artificial Intelligence,2013,26(9):865-871.

附中文参考文献:

[11] 杨章静,万鸣华,王巧丽,等．多流形的非监督线性差分投影算法[J]．计算机科学与探索,2016,10(11):1577-1586．

[12] 黄 璞,唐振民.无参数局部保持投影及人脸识别[J].模式识别与人工智能,2013,26(9):865-871.