改进的并网逆变器模型预测控制方法

张子成，陈阿莲，邢相洋

（山东大学控制科学与工程学院，济南 250061）

随着环境污染和能源短缺的不断加重，太阳能、风能等可再生能源得到快速发展，并网逆变器作为可再生能源发电系统和电网之间的接口，其性能将直接影响到电网的电能质量，因此并网逆变器的研究工作极具实际意义[1-2]。电流内环控制是三相并网逆变器的主要控制方法，国内外相关文献对此研究深入。文献[3]采用滞环控制的方法实现电流的控制，虽然具有很好的动态性能，但是谐波含量太大；文献[4]采用PI控制器，但是存在动态响应慢以及稳态误差的不足；文献[5]采用静止坐标系下的比例谐振控制器，该方法虽然能够消除稳态误差，但是比例谐振的参数难以调节。

预测控制是近年来发展起来的一类控制算法，它采用多步测试、滚动优化以及反馈校正等控制策略，具有鲁棒性高、动态性能好等优点[6]。近年来，预测控制被广泛应用于同步电机、有源滤波器APF（active power filter）、并网逆变器等电力电子领域[7-10]。

在预测控制方法中，有限集模型预测控制FCS-MPC（finite control set model predictive control）最为典型，其原理是根据采样值及开关状态推出下一时刻的电流输出值，并和给定值比较选出下一周期内最优的开关状态[11]。然而传统的FSC-MPC存在一定的缺点。首先，电流控制的精度偏低，开关状态的整周期作用使得电压矢量跟踪不准确；其次，开关状态选择不规律，电压矢量只是根据代价函数来选择，开关状态不均匀，经常出现多个桥臂同时动作的情况，这将使得系统脉动和电磁噪声增大[12]。

基于此，本文提出一种基于开关状态选择和矢量作用时间两个维度的预测控制方法，该方法在保证算法简单易行的基础上既能改善逆变器输出电流波形，又能保证桥臂动作规律，仿真和实验证明该方法控制性能优于传统的模型预测控制。

1 并网逆变器的数学模型

1.1 拓扑结构及模型分析

图1所示是典型的三相并网逆变器电路，图中，Udc为直流侧电压，idc为直流侧电流，C为直流侧稳压电容，L 为滤波电感，R 为回路电阻，ea、eb、ec分别为电网三相电网电压，ia、ib、ic分别为电网三相并网电流，其方向如图1所示。

图1 三相并网逆变器拓扑结构Fig.1 Topology of three-phase grid-connected inverter

根据基尔霍夫电压定律，逆变器的数学模型[13]为

式中，uNn为直流电压负端和电网公共端之间的电压，称为共模电压；uaN、ubN、ucN为逆变器输出电压，可以由开关状态和直流电压的函数表示。定义开关函数为

式中，x=a，b，c。则逆变器输出电压可表示为

通常采用电压矢量的方式来描述逆变器的输出电压。电压矢量定义为

式中，r定义为算子，r=ej2π/3。

在图1中， 开关函数 SaSbSc存在 000、001、010、011、100、101、110、111 共 8 种状态， 由式（3）可以在复平面中画出每一个开关状态所对应的电压空间矢量，8种不同的开关状态对应的矢量如图2所示。图2 中，8 个电压矢量分别用 u0，u1，···，u7表示，其中 u0、u7为零矢量,u1，u2，···，u6为有效矢量，幅值为2Udc/3。

图2 电压矢量Fig.2 Diagram of voltage vectors

表1 空间电压矢量对应关系Tab.1 Voltage space vectors and the corresponding components

定义 s为电压矢量的索引号， 则 s、u、Sa、Sb、Sc、α轴分量以及β轴分量的对应关系如表1所示。

1.2 逆变器模型的离散化

式（1）中共模电压uNn不易测量，为此利用恒幅值坐标变换将abc坐标系下的模型方程转换到αβ坐标系下，由于uNn经坐标变换后不存在对应α或β轴的分量，变换公式和变换结果如下

为了便于数字化实现，需要将模型进行离散化处理。在考虑环路电阻R的影响时，后向差分法比前向差分法离散精度更高，系统模型更准确。因此本文采用后向差分法进行离散化。后向差分离散公式和离散模型分别为

式中：Ts为采样时间；uα（k）、uβ（k）为电压矢量在 α轴和β轴上的分量，可由图2中的几何关系求得。

为了预测将来电流值，将式（7）等价转化为

由于采样频率远大于工作频率，下一k+1时刻的值通常用k时刻值来代替进行模型计算，但这样难免会带来一定误差，降低系统控制精度，为对其进行补偿，采用外推法来预测k+1时刻的值[15]。

式中，i*（k+1）为 k+1 时刻的给定值。

为了验证外推法的近似精度，通过仿真加以验证。以幅值150 V、频率50 Hz的电压为例，观察以k时刻代替的方法和外推法的不同效果，采样频率为10 kHz，外推法估计效果如图3所示。可以看出，前者的误差最高可达5 V，但后者的误差几乎为0，因此采用外推法进行模型计算更为精确。

图3 外推法估计效果Fig.3 Estimation effect of extrapolation method

2 模型预测控制原理

2.1 传统模型预测控制原理

模型预测控制 MPC（model predictive control）是一种基于系统模型的控制方法，其基本原理是利用系统模型来预测某一变量在预定的时间段内的行为，并根据该变量设计价值函数，通过比较求取使价值函数达到最小值的控制动作。MPC的主要思路[16]如下：①使用系统模型来预测变量的变化；②用价值函数表示系统的期望；③通过最小化代价函数确定控制动作。

MPC的控制原理如图4所示，通过比较选择使价值函数达到最小的开关状态投入使用。

图4 MPC原理Fig.4 Principle of MPC

并网逆变器控制的目的是实现电流跟踪给定值。为此，价值函数选为

2.2 改进模型预测控制原理

传统有限集模型预测控制存在控制精度偏低和开关状态不规律的缺点。为此，本文提出了一种简单易行的改进方案，该方案可以选出最佳的有效矢量并使有效矢量的作用时间也参与控制，这样既能提高控制精度，又能使开关状态的动作更加规律，每次仅有一个桥臂动作，减少系统脉动和电磁噪声。

根据等式变换，将式（8）变换形式[18]为

式（12）通过电网电压和给定电流在k+1时刻的估计值以及k时刻的电流采样值，根据逆变器模型计算出逆变器输出电压的估计值，uα、uβ为使电流跟踪到给定值的最佳矢量。如图5所示，传统算法选出u1作为最优矢量，并将其整周期投入使用，根据伏秒平衡原理可以看出，u1的整周期作用会造成矢量的跟踪效果达不到最佳，由几何原理知，电压矢量作用的最优时间为Teff，本文提出的改进控制算法是由该原理演绎得到。

图5 有效矢量最优作用时间Fig.5 Optimal effective time of effective vector

图6 区域分配Fig.6 Allocation of regions

在改进的预测控制算法中，首先进行有效矢量的挑选和有效矢量作用时间的计算，然后进行零矢量的选取以及开关序列的确定。前者可以保证较好的电流跟踪精度，后者则可以保证开关的规律切换以及较低的开关频率。其中，有效矢量的选择不再通过价值函数来选择，而是通过矢量区域来选择，如图6所示。

图6中两条虚线和αβ轴将平面分为6个区域，当电压矢量进入某一区域时，则选用相应的电压矢量，如当电压矢量进入第Ⅱ区域时，由于矢量作用端点距矢量u2所在方向的射线最短，因此选用u2作为下一周期投入使用的有效矢量。在其他区域时也依此规律选择。

与传统模型预测控制相比，本文提出算法的另一个不同是不再将选出的矢量整周期作用，而是计算出其最优作用时间，周期内剩余时间选用零矢量进行作用，这样既能保证电流控制准确，又能保证开关状态变化规律，每次切换仅有一个桥臂动作，从而可以降低开关损耗。

如图7所示，假设需要的矢量落在第Ⅱ区域，则选择u2作为有效矢量，为计算出有效时间Teff，由作用端点向u2做垂线，可得

6个有效矢量的模均为直流电压的2/3,由此可以求得最优作用时间Teff。当计算出的矢量落在其他区域时，可以依此类推，各区域矢量选择及最优作用时间如表2所示。

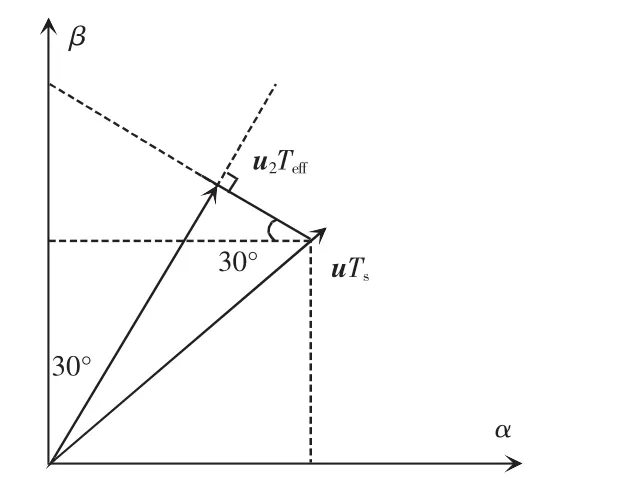
图7 最优作用时间计算Fig.7 Calculation of optimal effective time

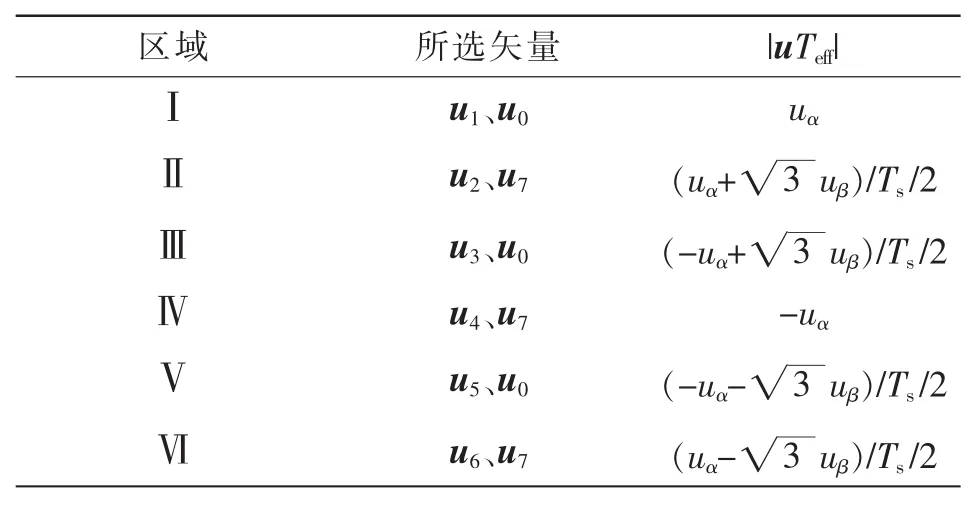
表2 矢量选择及最优作用时间计算Tab.2 Selection of voltage vectors and calculation of optimal effective time

表2中还列出了不同区域中所选择的零矢量的种类，即在Ⅰ、Ⅲ、Ⅴ区域中选择000，而在Ⅱ、Ⅳ、Ⅵ区域中选择111。零矢量的选择以降低开关频率和减小电磁脉动为原则，因此当有效矢量为100，010，001 时，选择的零矢量为 000，当有效矢量为110，101，011，选择的零矢量为111。如图8所示，以区域Ⅰ和Ⅱ为例，说明有效矢量和零矢量的作用顺序，可以看出，每次切换仅有一个桥臂动作。

图8描述了区域I和区域II的开关序列，首先是零矢量的选取，当有效矢量为 u1、u3、u5时，选择000作为相应的零矢量，当有效矢量为u2、u4、u6时，选择111作为相应的零矢量。其次是开关序列的确定，可以看出，零矢量嵌入在有效矢量中，每次仅有一个桥臂动作，保证了开关切换的规律性。

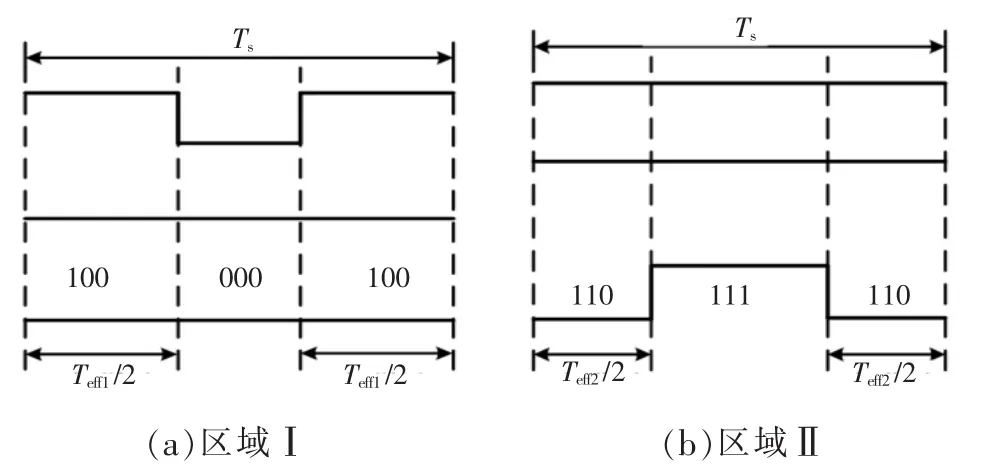
图8 矢量作用顺序Fig.8 Acting sequences of vectors

3 仿真与实验验证

3.1 仿真验证

为验证上述理论分析的合理性与可行性，用Matlab/Simulink分别对传统模型预测算法和改进算法进行仿真验证。两者的仿真参数一致，仅模型预测的算法不同，仿真参数如表3所示。

表3 仿真参数Tab.3 Simulation parameters

电流跟踪结果分别如图9、图10所示。图9（a）为传统模型预测控制方法下电流波形，可以看出该电流波形毛刺较多，精度偏低；图9（b）为加入有效矢量作用时间后的预测控制算法，可以看出三相电流波形变得平滑，跟踪精度明显改善。图10为旋转坐标系下d轴电流跟踪仿真结果，可以看出，在采用了改进算法后，电流的跟踪精度得到了显著提高。

使用Simulink的FFT分析功能对图9的电流进行傅里叶分析，结果如图11所示，传统预测控制算法下的电流畸变率为2.71%，而采用改进的算法后，电流畸变率降低到了1.51%。因此改进算法能够提高电流跟踪精度。

图9 电流跟踪精度Fig.9 Current tracking accuracy

图10 旋转坐标系下电流跟踪仿真波形Fig.10 Simulation waveforms of current tracking in rotating coordinate

图12是在一个周期内两种方法的开关状态选择，图（a）是传统模型预测算法的开关状态选择，图（b）是改进模型预测算法的有效矢量的选择。可以看出传统算法开关状态选择不规律，经常出现多个桥臂同时动作的情况，给系统带来较大的脉动和电磁干扰。采用改进的算法后，由于零矢量的作用内嵌在有效矢量作用的中间，因此可以保证每次切换仅有一个桥臂动作，从而改善了系统的性能。

图11 并网电流FFT分析Fig.11 FFT analysis of grid-connected current

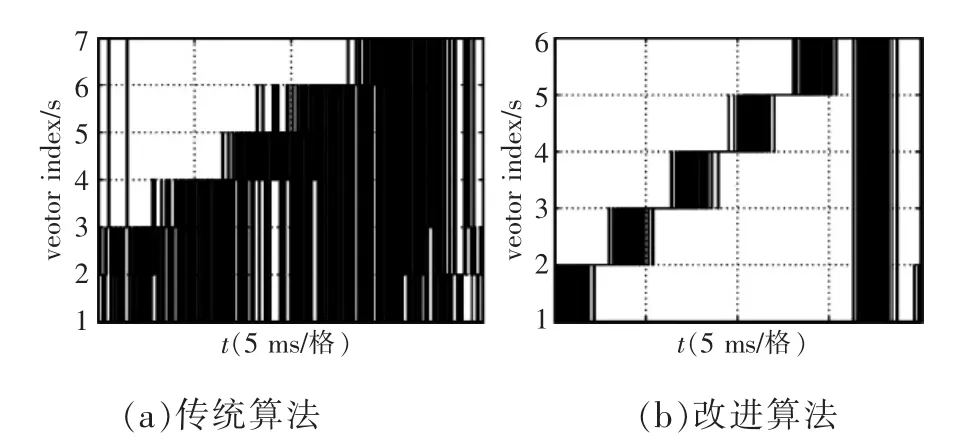
图12 开关状态选择Fig.12 Selection of switching states

3.2 实验验证

为了进一步验证算法的可行性，设计了基于一台10 kW的并网逆变器实验样机，实验参数与仿真参数一致，如表3所示。

实验结果如图13所示，可以看出，传统模型预测控制方法下的三相电流波形质量较差，精度偏低，将会给电网带来谐波污染；而采用改进的算法后，电流跟踪效果明显改善，谐波含量较少，能够实现稳定并网。

图13 三相并网电流波形Fig.13 Waveforms of three-phase grid-connected currents

4 结语

模型预测控制具有鲁棒性强、动态响应快等优点，在逆变器控制中应用广泛。针对传统预测控制开关状态切换不规律的缺点，本文提出了一种基于开关状态选择和矢量作用时间的预测控制方法，该方法既能保证算法简单易行，又能改善逆变器输出电流波形，保证开关管动作规律。通过仿真及实验验证，证明改进算法能够改善电流跟踪精度，同时使开关状态的切换更加规律，从而减少脉动和电磁噪声，使系统更加稳定。

参考文献：

[1]曾正,杨欢,赵荣祥,等．多功能并网逆变器研究综述[J].电力自动化设备,2012,32（8）:5-15.Zeng Zheng,Yang Huan,Zhao Rongxiang,et al.Overview of multi-functional grid-connected inverters[J].Electric Power Automation Equipment,2012,32（8）:5-15（in Chinese）.

[2]曾正,赵荣祥,汤胜清,等.可再生能源分散接入用先进并网逆变器研究综述[J].中国电机工程学报,2013,33（24）:1-12,21.Zeng Zheng,Zhao Rongxiang,Tang Shengqing,et al.An overview on advanced grid-connected inverters used for decentralized renewable energy resources[J].Proceedings of the CSEE,2013,33（24）:1-12,21（in Chinese）.

[3]顾和荣,杨子龙,邬伟扬.并网逆变器输出电流滞环跟踪控制技术研究[J].中国电机工程学报,2006,26（9）:108-112.Gu Herong,Yang Zilong,Wu Weiyang.Research on hysteresis-band current tracking control of grid-connected inverter[J].Proceedings of the CSEE,2006,26（9）:108-112（in Chinese）.

[4]朱炜锋,窦伟,徐正国,等.基于PI控制的三相光伏并网逆变器电流控制器设计[J].可再生能源,2009,27（2）:55-58.Zhu Weifeng,Dou Wei,Xu Zhengguo,et al.Design of the Pi current controller of three phase photovoltaic grid-connected inverter[J].Renewable Energy Resources,2009,27（2）:55-58（in Chinese）.

[5]胡巨,赵兵,王俊,等.三相光伏并网逆变器准比例谐振控制器设计[J].可再生能源,2014,32（2）:152-157.Hu Ju,Zhao Bing,Wang Jun,et al.Design for quasi proportional resonat controller of three-phase photovoltaic grid connected inverter[J].Renewable Energy Resources,2014,32（2）:152-157（in Chinese）.

[6]席裕庚.预测控制[M].北京:国防工业出版社,1993.

[7]Le-Huy H,Slimani K,Viarouge P.Analysis and implementation of a real-time predictive current controller for permanent-magnet synchronous servo drives[J].Industrial Electronics,IEEE Transactions on,1994,41（1）:110-117.

[8]吴勇,徐金榜,王庆义,等.并联有源电力滤波器电流预测控制[J].华中科技大学学报:自然科学版,2008,36（4）:99-102.Wu Yong,Xu Jinbang,Wang Qingyi,et al.Current predictive control of shunt active power filter[J].Journal of Huazhong University of Science and Technology:Natural Science Edition,2008,36（4）:99-102（in Chinese）.

[9]Vargas R,Cortés P,Ammann U,et al.Predictive control of a three-phase neutral-point-clamped inverter[J].IEEE Transactions on Industrial Electronics,2007,54（5）:2697-2705.

[10]杨勇,赵方平,阮毅,等.三相并网逆变器模型电流预测控制技术[J].电工技术学报,2011,26（6）:153-159.Yang Yong,Zhao Fangping,Ruan Yi,et al.Model current predictive control for three-phase grid-connected inverters[J].Transactions of China Electrotechnical Society,2011,26（6）:153-159（in Chinese）.

[11]Kouro S,Cortés P,Vargas R,et al.Model predictive control—A simple and powerful method to control power converters[J].Industrial Electronics,IEEE Transactions on,2009,56（6）:1826-1838.

[12]李永东.交流电机数字控制系统[M].北京:机械工业出版社,2002.

[13]徐德鸿.电力电子系统建模及控制[M].北京:机械工业出版社,2005.

[14]Cortes P,Rodriguez J,Antoniewicz P,et al.Direct power control of an AFE using predictive control[J].IEEE Transactions on Power Electronics,2008,23（5）:2516-2523.

[15]Kukrer O.Discrete-time current control of voltage-fed threephase PWM inverters[J].IEEE Transactions on Power Electronics,1996,11（2）:260-269.

[16]Rodriguez J,Cortes P.Predictive control of power converters and electrical drives[M].New Jersey:John Wiley&Sons,2012.

[17]Rodriguez J,Pontt J,Silva C,et al.Predictive current control of a voltage source inverter[J].IEEE Transactions on Industrial Electronics,2007,54（1）:495-503.

[18]Barros J D,Silva J F A,Jesus E G.Fast-predictive optimal control of NPC multilevel converters[J].IEEE Transactions on Industrial Electro-nics,2013,60（2）:619-627.