基于参数扰动的混沌控制方案在Buck-Boost变换器中的应用研究
杨昌烨,陈艳峰,张 波,丘东元,陈 曦
(华南理工大学电力学院,广州 510640)
在面向光伏发电的直流微电网系统设计中,常常设计光伏阵列的开路电压高于直流侧母线电压;而光伏阵列受温度降低、日照不足等环境因素影响时又会低于直流侧母线电压,所以连接大电网的接口变换器须具有升、降压功能[1],其中以基本的Buck-Boost变换器最为常用。峰值电流控制型的Buck-Boost变换器是一个典型的强非线性系统,运行状态很容易受到参考电流、输入电压等电路参数的影响,并出现倍周期分岔、边界碰撞分岔、混沌等非线性动力学现象,使系统无法稳定运行[2-4]。因此,需要通过有效的控制方案使进入混沌态的变换器重新回到周期态稳定运行。
自20世纪90年代美国学者提出OGY法[5]以来,混沌控制逐渐成为研究热点。根据是否有待控目标轨道,这些混沌控制方法可归纳为两大类:一类是基于混沌态的周期遍历特性,在混沌吸引子中找到一条周期轨道并将系统稳定在这条轨道上,从而使得系统回到稳定运行状态,如OGY法[5]、外加参数扰动法和开关切换法[6-7]、状态反馈精确线性化的解耦控制[8]等;另一类控制没有特定的控制目标轨道,控制的关键在于使系统的李雅普诺夫指数下降为负值,从而使系统稳定到一条新的周期轨道,如参数共振微扰法[9]、自适应斜坡补偿法[10]。
2015年陈关荣等提出了基于参数扰动的混沌控制方法,文献[12]将该方法应用于开关电感Boost变换器的混沌控制当中,使变换器的性能得以改善。本文进一步将该方法用于Buck-Boost变换器,设计了适用于峰值电流控制型Buck-Boost变换器的混沌控制方案,分析了该方案在改善变换器的动态性能、输出纹波等性能的影响,并通过仿真和实验验证了该方案的有效性。
1 峰值电流控制的Buck-Boost变换器的建模与非线性动力学行为
峰值电流控制模式Buck-Boost变换器的电路原理如图1(a)所示。在变换器工作于电感电流连续模式 CCM(continuous-conduction mode)的情况下,根据开关管ST和二极管D导通情况,变换器在1个周期内存在2个不同的工作状态,当时钟信号来临时,开关管ST导通,二极管 D截止,电感 L充电;当电感电流iL上升至Iref时,开关管ST关断,二极管D导通,电感 L和电容对负载提供电能,此时电感电流iL下降。直到下一周期时钟到来,开关管ST再次导通。电感电流iL与时钟周期信号Clock工作波形如图1(b)所示。
取电感电流iL和电容电压uC为状态变量,在CCM下,对应两个电路的状态方程分别为

图1 变换器原理与电感电流iL波形Fig.1 Schematic of converter and waveform of iL

式中:x=[iL,uC]Tr;E 为输入电压;T 为开关周期;τ1为模态切换的时间,τ1=dnT;dn为第n个开关周期的占空比,Ai(i=1,2)和 Bi(i=1,2)为系数矩阵分别表示为
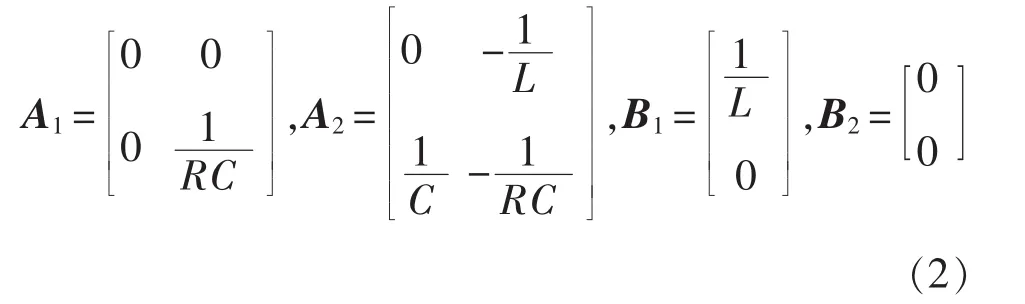
求解式(1)中分段线性方程组,可得到第n+1个开关周期开始时刻的状态变量xn+1和第n个开关周期开始时刻的状态变量xn的频闪映射,即

选取电路参数:T=40 μs(f=25 kHz),L=0.325 mH,R=20 Ω,C=10.6 μF,E=8 V,Iref=0~2.5 A。根据频闪映射模型式(3),可得到电感电流iL和电容电压uC随参考电流Iref变化的分岔图,进而得到电路进入周期态、混沌态的参数区域,如图2所示。
在参考电流Iref由0 A增加到2.5 A的过程中,变换器首先在Iref=0.95 A时出现倍周期分岔,由稳定的周期-1态变为周期-2态,此时占空比为0.48,电压增益G=0.923。此后,随着参考电流的增大,系统经过多次倍周期分岔后最终进入了混沌状态。从图中可以看到,系统处于混沌状态时,单一的Iref值往往对应多个周期轨道。本文的目标即是在这些轨道中,选取所需UPO-1并使之固定下来,使处于混沌状态的变换器重新回归周期-1态工作,并使变换器输出电压纹波等性能指标得以改善。

图2 以Iref为分岔参数时的分岔图Fig.2 Bifurcation diagrams of state variables with Irefas bifurcation parameter
2 基于参数扰动法的混沌控制方案及其应用
2.1 基于参数扰动的混沌控制方法简介
基于参数扰动的混沌控制方法[12]是由Alexander、陈关荣等学者于2015年提出的一种新型混沌控制方法,对于处在混沌状态的多维系统,通过对系统中所选取的一个参数添加扰动,可以使系统固定于混沌吸引子中的一个不稳定周期轨道(UPO)。对于二维系统,仅需要对控制变量进行两步扰动便可实现混沌控制,即

式中:xn∈R2;F(·)是光滑矢量函数;pn是每个周期的控制变量。定义不动点,则在目标轨道的邻域内,系统可线性近似表示为

由式(5)可得
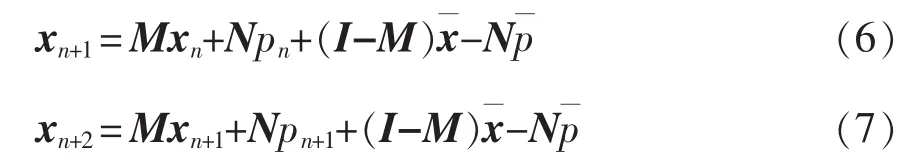
将式(7)代入式(6)可得到

当系统满足周期-1稳态时,有xn+2=x,从而可得到二维系统的两步扰动值为

即每个周期控制参数需要调整为
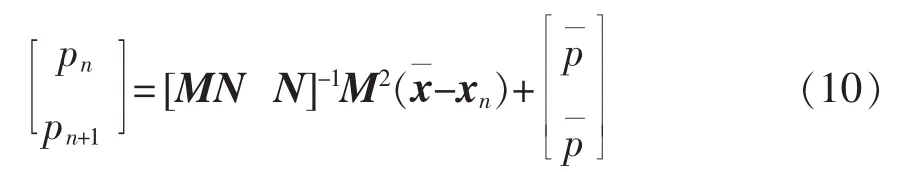
2.2 控制参数计算
令式(3)中xn=xn+1,可以求出混沌状态下的不动点为

由式(3)、式(5)计算得参数矩阵和系数矩阵为

由式(10)可求得,加入参数扰动混沌控制方法后,第n和第(n+1)周期参考电流值为

2.3 仿真验证
根据前文介绍的混沌控制方法原理和相关参数计算,设计了适用于开关变换器的混沌控制新方案,并利用PSIM电路仿真软件,搭建电路仿真模型。其中,控制电路是在传统峰值电流控制模式基础上增加了一个扰动量计算单元。其工作原理是在每周期开始时采集状态变量,根据式(13)计算得到本周期的参考电流,最后可以得到如图3所示状态变量iL和uC的时域波形。
由图3(a)可见,0~0.03 s时,参考电流为 2.1 A时,电路工作在混沌状态;0.03 s时,本混沌控制方案开始工作,扰动量计算单元计算参考电流在每个开关周期的修正值,系统从混沌状态被控制到周期-1态稳定工作。结合图3(b)的相轨图分析,可以看出,被控UPO-1轨道存在于原混沌吸引子中,在控制过程中并没有产生新的周期轨道。
电感电流功率谱如图4所示。可以看出通过参数扰动法,功率谱由连续的混沌态变为离散的周期态,即处于混沌状态的Buck-Boost变换器可以通过本混沌控制方法重新工作在UPO-1轨道中。
由图3(a)可以得到被控周期-1态的占空比d=0.67,输出电压平均值为15 V,增益G=2.03。相较于图2的电感的电流iL第1次分岔时的d=0.48和G=0.923有了较明显的提升。电流纹波峰峰值从混沌状态下的1.5 A控制到周期-1轨道的0.5 A,电压纹波峰峰值从混沌状态下的3.5 V控制到周期-1轨道的1.2 V,纹波明显下降。可见,通过参数扰动混沌控制,Buck-Boost变换器电感电流及输出电压纹波特性得到了显著改善。

图4 控制前后电感电流功率谱Fig.4 Power spectrum of iLwith and without control
3 实验验证
为验证上述理论分析与仿真结果的正确性,搭建了实验平台,实验电路的主要参数与Psim仿真中参数相同,选择功率开关管型号为IRF640B,二极管型号为MUR1560G,采用CSM005LX霍尔传感器采样电感电流,以LM324N搭建差分电路采样输出电压。
实验波形如图5所示,图中的电流、电压通过霍尔元件转换为电压,再通过示波器测得,电流、电压转换比为1:1。调节参考电流Iref,可以看到Buck-Boost变换器的电流波形从图5(a)中的周期1态,到分岔后的图5(b)中的周期 2态,再到图5(c)中的混沌态。
由图2可见,峰值电流控制的Buck-Boost变换器在参考电流Iref<0.95 A时处于周期1态,Iref>0.95 A时发生倍周期分岔,在Iref=2 A时已经处于混沌态,可以明显看出图5中的实验结果与理论、仿真结果相符。
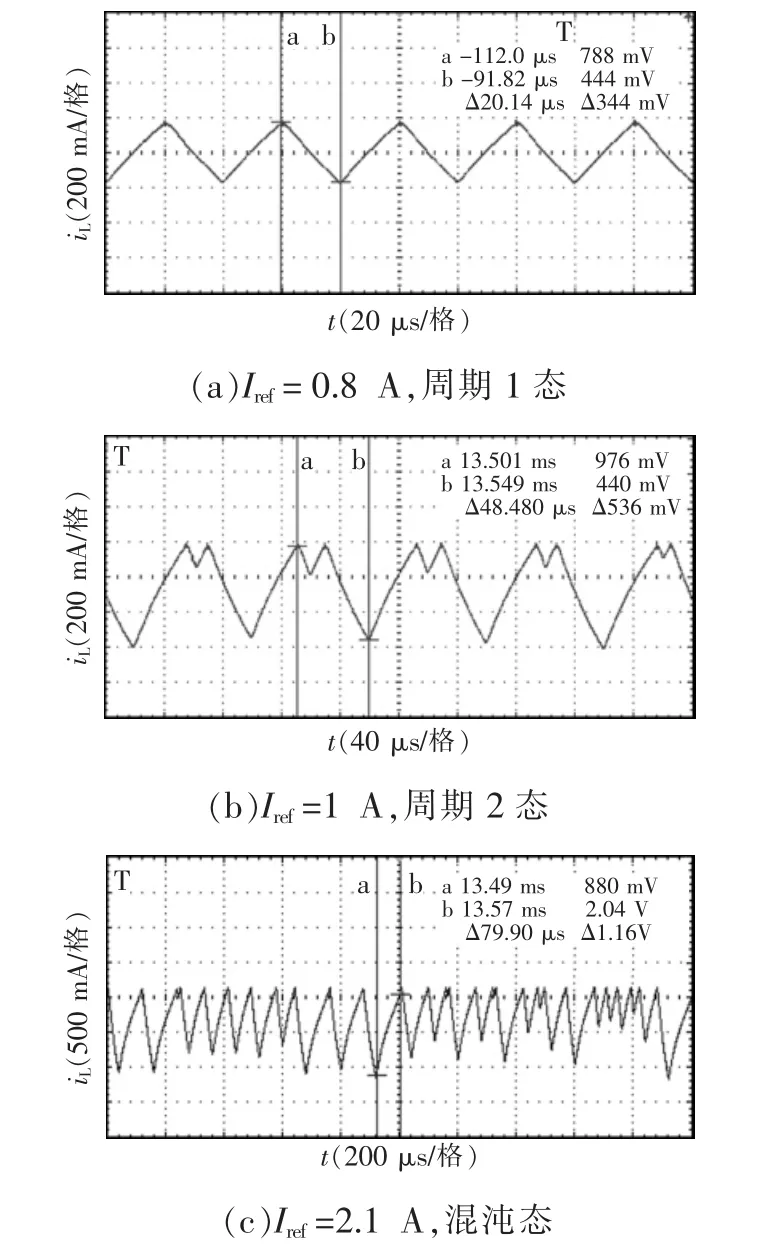
图5 Buck-Boost变换器电感电流iL波形Fig.5 Waveforms of iLof Buck-Boost converter
选定Iref=2.1 A,通过DSP F28335对变换器进行采样计算并添加扰动控制,通过DSP控制器,在每个周期对电感电流和输出电压采样并进行扰动量计算,与参考电流Iref叠加得到新的控制参数,通过RS触发器后获得新的调制脉冲,实现对变换器的混沌控制。实验波形结果如图6所示。从图6中可以看到,原本处于混沌状态的Buck-Boost变换器被控制到了稳定的周期-1态。电感电流和输出电压纹波如表1所示。由表1可知,实验输出电压与电感电流的纹波与Psim仿真结果基本一致。

图6 混沌控制下Buck-Boost变换器输出实验波形Fig.6 Experimental waveform of output for Buck-Boost converter under chaotic control

表1 电感电流和输出电压纹波Tab.1 Ripples of inductor current and output voltage
4 结语
本文首先对Buck-Boost变换器中的非线性动力现象及混沌现象进行分析,并将参数扰动混沌控制方法应用于Buck-Boost变换器,设计了适用于Buck-Boost变换器的混沌控制方案。通过理论分析、数值仿真与实验验证,其结果表明峰值电流控制的Buck-Boost变换器在参考电流增大之后由稳态进入到了混沌态,加入参数扰动的混沌控制之后,重新回到周期1态(UPO-1),并且没有产生新的周期轨道,证实了该控制方案可以有效提高变换器电压增益,减小电感电流和输出电压纹波,使得变换器工作特性得到显著改善。
参考文献:
[1]杨晨,谢少军,毛玲,等.基于双管Buck-Boost变换器的直流微电网光伏接口控制分析[J].电力系统自动化,2012,36(13):45-50.Yang Chen,Xie Shaojun,Mao Ling,et al.Analysis on control strategy of two-switch buck-boost converter for photovotaic interface in DC microgrid[J].Automation of Electric Power Systems,2012,36(13):45-50(in Chinese).
[2]Tse C K.Complex behavior of switching power converters[M].Boca Raton,USA:CRC Press LLC,2004:1-26.
[3]Cheng K W E,Liu M,Wu J.Chaos study and parame-terspace analysis of the DC-DC buck-boost converter[J].IEEE Proceedings of Electronics Power Application,2003,150(2):126-138.
[4]张波,李萍,齐群.DC-DC变换器分叉和混沌现象的建模和分析方法[J].中国电机工程学报,2002,22(11):81-86.Zhang Bo,Li Ping,Qi Qun.Methods for analyzing and modeling bifurcations and chaos in DC-DC converter[J].Proceedings of the CSEE,2002,22(11):81-86(in Chinese).
[5]Ott E,Grebogi C,Yorke J A.Controlling chaos[J].Physical Review Letters,1990,64(11):1196-1199.
[6]Podder G,Chakrabarty K,Banerjee S.Experimental control of chaoticbehavior of buck converter[J].IEEE Transactions on Circuits and Systems-I,1995,42(8):502-504.
[7]Podder G,Chakrabarty K,Banerjee S.Control of chaos in the boost converter[J].Electronics Letters,1995,31(11):841-842.
[8]邓卫华,张波,胡宗波,等.CCM Buck变换器的状态反馈精确线性化的非线性解耦控制研究[J].中国电机工程学报,2004,24(5):120-125.Deng Weihua,Zhang Bo,Hu Zongbo,et al.Research of nonlinear decoupled control law using state variable feedback linearization method based on the CCM buck converter[J].Proceedings of the CSEE,2004,24(5):120-125(in Chinese).
[9]周宇飞,陈军宁,谢智刚,等.参数共振微扰法在 Boost变换器混沌控制中的实现及其优化[J].物理学报,2004,53(11):3676-3683.Zhou Yufei,Chen Junning,Tse C K,et al.Application of resonant parametric perturbation to the chaos control in Boost converter and its optimization[J].Acta Physica Sinica,2004,53(11):3676-3683(in Chinese).
[10]来新泉,李祖贺,袁冰,等.基于自适应斜坡补偿的双环电流模DC/DC混沌控制[J].物理学报,2010,59(4):2256-2264.Lai Xinquan,Li Zuhe,Yuan Bing,et al.Control of chaos in double-loop current-mode DC/DC based on adaptive slope compensation[J].Acta Physica Sinica,2010,59(4):2256-2264 (in Chinese).
[11]Jimenez-Trianna A,Chen Guanrong,Gauthier A.A parameter-perturbation method for chaos control to stabilizing UPOs[J].IEEE Transactions on Circuits and Systems-II,2015,62(4):.407-411.
[12]李姿,陈艳峰,张波,等.开关电感Boost变换器的失效机理及基于参数扰动的混沌控制方案研究 [J].电源学报,2017,15(3):148-155.Li Zi,Chen Yanfeng,Zhang Bo,et al.Study on failure mechanism of switched-inductor boost converter and chaos control scheme based on parameter-perturbation[J].Journal of Power Supply,2017,15(3):148-155(in Chinese).

