三电平直流变换器的交错式PWM方法
刘 威,吕征宇
(浙江大学电气工程学院,杭州 310027)
由于功率开关管的电压应力仅是输入电压的一半,三电平结构被广泛应用于高压场合,如三相功率因数校正电路的后级等。在常用的几种三电平半桥结构中,桥臂串联型三电平结构使用的元件最少,不需要任何箝位二极管与飞跨电容,调制方法也最为灵活[1-6]。
输入分压电容和隔直电容的均压是三电平变换器正常工作的前提[7-8]。在实际电路中,驱动电路延时、开关管和输入分压电容等参数的不一致,均可能导致偏压,从而导致主功率管电压应力增加、整流二极管电流应力不一致、变压器偏磁等问题。因此,必须对输入分压电容电压等进行均压控制。目前主要有两类方法:一是添加辅助电路[7]或者构造相应拓扑[9-11]实现自动均压;二是使用反馈控制的方法,在控制电路中添加一个均压环[13-15]。
自动均压似乎是一个很好的解决方案。通过引入一个飞跨电容,并在不同的电路阶段交替将两个输入分压电容与该飞跨电容并联,从而保证三者的电压相等[9-11]。然而,这些拓扑只能使用频率调制,无法使用对称脉冲宽度调制PWM(pulse width mo-dulation)方法,因为引入的飞跨电容不允许其使用(S1,S4)和(S2,S3)等开关组合,其中(Sx,Sy)表示 Sx和Sy同时导通。此外,当分压电容与飞跨电容之间存在电压差时,直接并联会引起较大的电流尖峰[12]。
除了在主电路中增加元件,也可以使用反馈控制的方法实现电容均压。在均压环中,存在2个被控量——输入分压电容电压和隔直电容电压。因此,需要两个控制量,通常选择驱动信号的占空比和相位差,即图1(b)中的 Dp、Dn和 PS。在文献[13,14]中,针对非隔离型三电平变换器,由于不含隔直电容,将相位差固定为180°,仅调节占空比来实现输入分压电容的均压。对于桥臂串联型三电平半桥拓扑,文献[15]通过调节占空比来平衡隔直电容电压,同时调节正、负半周之间的相位差来均衡输入分压电容的电压。然而,其需要隔离采样输入电压、输入分压电容电压和隔直电容电压等3个电压,同时,由于控制量与被控量之间的相互耦合关系,控制电路的参数设计比较复杂。
本文提出了一种新颖的PWM方法。与传统PWM方法相比,该方法可以将隔离电容的电压始终保持在输入电压的一半左右,大大简化了采样电路和均压控制方案。
1 传统PWM调制
图1为三电平半桥LLC谐振变换器的原理图及传统PWM调制时的主要波形。Cd1、Cd2为输入分压电容,S1~S4是开关管,C1~C4为其等效输出电容,谐振电感Lr、励磁电感Lm和谐振电容Cr构成LLC的谐振腔,Cr同时还具有隔直的作用。Dp、Dn分别为正、负半周占空比,Tpc和Tnc是Cd1和Cd2的充放电时间。PS是正半周期和负半周期之间的相位差。vAB为A、B两点间的电压差,VAB是其平均值。Vin为输入电压,Cd1和Cd2上的电压纹波非常小,后续分析中将使用其直流分量Vcd1和Vcd2代替。Vcr是Cr的平均电压。ir和im分别为谐振电流和励磁电流,id为输入分压电容的净充放电电流。

图1 桥臂串联型三电平半桥LLC谐振变换器Fig.1 Leg-series three-level half-bridge LLC resonant converter
理想情况下,变换器的各参数和开关管的驱动信号都是对称的,即Dp=Dn,Tpc=Tnc。因此各电容电压均等于其理想值,Vcd1=Vcd2=Vcr=Vin/2。然而,在实际电路中,由于驱动电路延时、开关管和输入分压电容参数等不一致,会导致上述电压偏离理想值。
文献[15]声明隔直电容电压Vcr只受占空比影响,即

而Vcd1和Vcd2与占空比和相位差均有关。但严格来说,式(1)并不准确,Vcr不仅与占空比相关,还与Vcd1或 Vcd2有关。由于 Vcr和 Vcdx(x=1,2)都受到占空比和相位差的影响,所以必须仔细设计均压控制环的参数,否则该耦合关系很容易导致电容电压的低频振荡。
2 交错式PWM方法
对于图1中的拓扑,为保证输入分压电容的电荷平衡,存在两种PWM方法,如图2所示。对后级电路来说,二者的区别在于Tpc和Tnc期间vAB的幅度不同,PWM1时等于 Vcd1,而 PWM2时等于Vcd2。该拓扑不允许使用移相调制,否则Tpc和Tnc期间会对某一分压电容一直充电或放电。

图2 传统PWM方法Fig.2 Traditional PWM methods
稳态时,电感两端的平均电压为0,因此隔直电容电压平均值等于谐振腔输入电压平均值,即
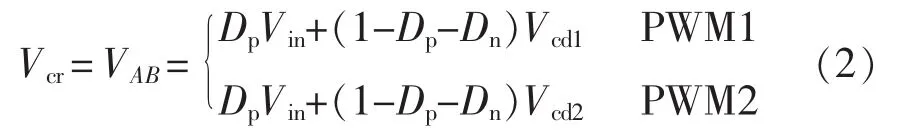
将式(2)中的2个表达式相加再除以2,可得

上述过程可以通过在相邻2个开关周期中交替使用PWM1和PWM2实现,如图3所示,因此称为交错式PWM调制。式(3)表明Vcr仅与占空比的差值有关,不再受Vcdx影响。在实际电路中,虽然占空比的差异不可避免,但该差值通常非常小,不会导致Vcr的显著偏差。例如,当|Dp-Dn|=1%时,Vcr的偏离程度也仅有1%,甚至低于隔离采样的误差。因此使用交错式PWM调制时,不再需要采样Vcr。
交错式PWM调制方法可以使用数字控制器轻松实现。以TI公司的C2000系列DSP为例,一个DSP芯片具有多个EPWM模块,每个EPWM模块包括一个计数器CTR(counter)和一个比较寄存器CMPR(compare register), 可以产生2路PWM信号,用来驱动2个开关管。如图3所示,CTR1和CMPR1分别是S1和S2的载波信号和调制信号,CTR2和CMPR2是S3和S4的载波信号和调制信号。PRD为开关周期,Duty是用于调节占空比的参数。由图可见,PWM1 的 CMPR1 等于 (PRD-Duty),PWM2 的CMPR2等于Duty。因此,在交错式PWM调制中,CMPR1和CMPR2在相邻的两个开关周期内需在PRD-Duty与Duty之间切换,而这可以通过在CTR等于0时更新CMPR来实现。使用传统PWM调制时,由于输出电压或输出电流闭环,CMPR也需要每个开关周期进行更新。因此,交错式PWM调制并没有带来软件计算量的增加。

图3 交错式PWM调制方法Fig.3 Interleaved PWM method
2.1 偏压原理
在实际电路中,不同的延时和占空比损失等问题会导致不对称的驱动信号,进而导致电容电压失衡。交错式PWM调制的驱动信号不一致可以归纳为2种情况:①载波信号的相位差不等于0;②正、负半周的占空比不相等。其主要波形如图4所示。
2.1.1 相位差不等于0
若S3和S4驱动电路中的延时比S1和S2的更长,则可等效为载波信号CTR2滞后于CTR1,此时电路的主要波形如图4(a)所示。由于正、负半周的占空比仍相等,即Dp1+Dp2=Dn1+Dn2,根据式 (3)有Vcr=Vin/2。此时 Tpc1=Tnc2<Tnc1=Tpc2, Tpc1和 Tnc2期间 id<0,说明 Cd1处于放电状态;Tnc1和 Tpc2期间 id> 0,Cd1充电。与驱动对称时相比,Cd1的放电时间减少、充电时间增加,因此 Vcd1>Vcd2。
2.1.2 正、负半周占空比不相等
若相邻2个周期的CMPR值之和不等于PRD,则正、负半周占空比不相等。当其和大于PRD时,Dp>Dn;反之,则 Dp<Dn。
Dp>Dn时的关键波形如图4(b)所示,其中相邻2个周期的CMPR1之和与CMPR2之和均等于PRD+delta,大于 PRD。根据式(3)可知,此时 Vcr>Vin/2。

图4 驱动不对称时的运行情况Fig.4 Operation under asymmetrical driving signals
此时相邻2个周期中各对应的时间量是相等的, 即 Dp1=Dp2、Dn1=Dn2、Tpc1=Tpc2、Tnc1=Tnc2。Tpc1时 Cd1放电,Tpc2时 Cd1充电。假设 Vcd1>Vcd2,则 Tpc1期间 vAB较大,导致ir的下降速度变慢,因此Cd1的放电量将增加;同时,Tpc2期间vAB较小,ir的下降速度变快,使Cd1的充电量减小。此消彼长之下,Vcd1将减小而Vcd2将增加,并最终相等,即Vcd1=Vcd2。
因此,可以得出结论:当CTR1和CTR2之间的相位差不为0时,如果CTR2滞后于CTR1,则Vcd1将大于Vcd2,同时Vcr不受影响。当Dp不等于Dn时,如果 Dp> Dn,Vcr将大于 Vin/2 且与 Dp和 Dn之间的差成比例,同时Vcd1和Vcd2不受影响。
2.2 均压策略
经过对偏压原理的分析可知,使用交错式PWM调制方法时,Vcdx与Vcr、相位差与占空比之间是两两解耦的,即Vcdx仅与载波间的相位差有关,而Vcr仅与Dp和Dn的差有关。同时,相位差与占空比差值的调节也是相互独立的。这种解耦的关系大大简化了均压控制方案的复杂度。
图5为采样及控制电路框图,其中包含2个完全独立的控制环路:输出电压环及输入分压电容电压环。在PWM调制中,输出电压和功率的调整通过改变占空比实现,即Dp=Dn=Duty/PRD。实际驱动电路中普遍存在的问题,如延时和占空比损失不一致等,会导致轻微的占空比差异。但是,当使用交错式PWM方法时,该差异对Vcr的影响很微弱,其值仍可以维持在理想值附近。因此,可以不再采样和控制Vcr,只需要平衡输入分压电容电压即可,而这可以通过调节CTR1与CTR2之间的相位差实现。
Vcd2与Vin共地,因此只需要一个光耦,而使用传统PWM方法时,则需要3个光耦[15]。此外,数字控制器的采样引脚无法识别负电压,所以在采样电路中加入了偏置电压Vbias。因此,运放的输出电压ΔVcd的计算公式为

式中:Rp1=[(R4∥R6)+R5]∥R7;Rp2=[(R3∥R7)+R5]∥R6;K的取值由Vin和采样引脚的输入电压范围决定;Vref为参考电压,可使用TL431获得,取为2.5 V。Vbias可通过电阻分压调节,为提高采样精度,可取为1.6 V,因为数字控制器的采样引脚的输入电压范围通常为0~3.3 V。
偏差信号ΔVcd经光耦隔离后,再经过一个PI控制器,便可调节载波信号CTR2的相位。若Vcd2小于 Vin/2,则 ΔVcd>Vbias,将提前 CTR2 的相位,使其超前于CTR1;反之,则延迟CTR2。
此外,当占空比等于0.5时,交错式PWM与两种传统PWM再无区别,均变成频率调制。但是该均压控制方法仍有效,即仅调节CTR2的相位来均衡输入分压电容电压。隔直电容电压始终在其理想值附近,无需控制。
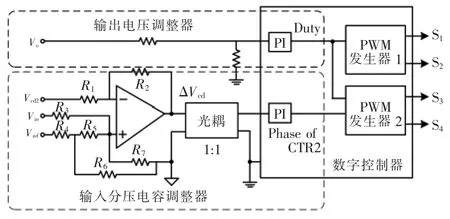
图5 均压控制电路框图Fig.5 Block diagram of voltage-galancing control circuit
3 实验验证
实验原理图如图1(a)所示,样机的主要参数如下:Cd1=Cd2=40 μF,Lr=63 μH,Cr=33 nF,Lm=370 μH,变压器匝比 34:1,S1~S4为 IPP65R190CFD,Co=2.64 mF,D5~D6为 BSC010NE2LS,Vin=400 V, 开关频率fs=100 kHz,输出电压 Vo=5.5 V,输出电阻 Ro=1 Ω。数字控制器为TMS320F28035,PWM发生器的时钟频率为 60 MHz, 因此 PRD=60 MHz/(2×100 kHz)=300。
图6为不对称驱动下的实验波形。为了使实验条件与理论分析尽可能一致,对4路驱动电路的延迟时间和占空比损失进行了校正,使其尽量一致,而不对称的驱动信号由数字控制器直接产生。
相位不对称时的实验波形如图6(a)所示,其中CTR2滞后CTR1的时间为333 ns,等于开关周期的3.33%。同时,CMPR1和CMPR2以图4(b)的方式在105~195之间切换,使Dp=Dn=0.35。由实验波形可知:Vcd1>Vcd2, 与理论分析结果一致;Vcr=201.7 V,非常接近计算值200 V。
不对称占空比下的实验波形如图6(b)所示,其中 Dp=0.35,Dn=0.25,CTR1 与 CTR2 同相。CMPR1和CMPR2在105~225之间切换。可知,Vcr=220.2 V,与计算值220 V吻合很好。同时,两输入分压电容电压相等,Vcd1=200.6 V、Vcd2=200.7 V。需要说明的是,为了清晰地体现电压不均衡,选择了很大的驱动信号不对称度。通常情况下,实际电路中的占空比差异远小于0.1,因此Vcr可以始终维持在Vin/2附近。
图6不仅证明不对称的驱动信号会导致电容电压失衡,而且还表明可以通过调整CTR2的相位来校正Vcdx,而Vcr仅与Dp与Dn的差值成正比。

图6 驱动不对称时的实验波形Fig.6 Experimental waveforms with asymmetrical driving signals
图7给出了带与不带均压控制时的实验波形。在图7(b)中,均压控制被禁用,尽管数字控制器产生的驱动信号是对称的,但由于驱动电路和主电路的不对称性,2个输入分压电容并不均压,Vcd1≠Vcd2。但是由于交错式PWM的使用,VAB=201.0 V,即Vcr=201.0 V,隔直电容电压基本平衡。图7(a)描绘了均压控制由禁止到使能时的转换过程,并提供了CTR2的相位轨迹。CTR2的相位本是数字控制器中的一个寄存器,通过线性的数模转换显示在实验波形中。幅度等于1.65 V表示CTR2与CTR1同相;若幅度大于1.65 V,则表明CTR2超前CTR1,反之,CTR2滞后CTR1。因此,如图7所示,当均压控制被禁用时,CTR2与CTR1同相;使能后,由于反馈控制,CTR2的相位被提前,以平衡输入分压电容电压Vcdx。最终,如图7(c),实现了 Vcdx的均压,Vcd1=Vcd2,且Vcr=VAB=200.9 V。以上过程验证了所提均压控制的有效性。

图7 带和不带均压控制时实验波形Fig.7 Experimental waveforms with and without the voltage-balancing control
4 结论
本文提出了一种用于半桥三电平直流变换器的交错式PWM方法,并在对其偏压原理进行分析的基础上,提出了相应的均压控制方案。实验结果验证了理论分析的正确性和所提方法的有效性。相比于传统PWM方法,该方法的主要优点有:
(1)将输入分压电容电压与占空比、隔直电容电压与相位差的关系解耦。正、负半周的占空比差值仅影响隔直电容电压,载波间的相位差只影响输入分压电容电压。因此,控制电路的设计更简单,结果更易于稳定。
(2)只需要1路隔离采样,降低了成本。
此外,该交错式PWM调制也适用于飞跨电容型半桥三电平变换器。均压控制策略在使用频率调制的场合仍然适用。
参考文献:
[1]Gu Yilei,Lu Zhengyu,Hang Lijun,et al.Three-level LLC series resonant DC/DC converter[J].IEEE Transactions on Power Electronics,2005,20(4):781-789.
[2]Chen Wu,Ruan Xinbo,Zhang Rongrong.Zero-voltageswitching PWM three-level converter with interleaved complementary modulation[C].IEEE Applied Power Electronics Conference and Exposition,2007:949-954.
[3]Canales F,Barbosa P M,Burdio J M,et al.A zero-voltage switching three-level dc/dc converter[C].International Telecommunications Energy Conference,2000:512-517.
[4]Barbi I,Gules R,Redl R,et al.DC-DC converter:four switches Vpk=Vin/2,capacitive turn-off snubbing,ZV turnon[J].IEEE Transactions on Power Electronics,2004,19(4):918-927.
[5]Ren Ren,Liu Bo,Jones E A,et al.Dual-output,three-level GaN-based dc-dc converter for battery charger applications[C].IEEE Applied Power Electronics Conference and Exposition,2016:2441-2448.
[6]刘威,姚文熙,吕征宇.半桥三电平LLC谐振变换器的调制方法[J].浙江大学学报:工学版,2017,51(8):1653-1661.Liu Wei,Yao Wenxi,Lu Zhengyu.Modulation methods of half-bridge three-level LLC resonant converters[J].Journal of Zhejiang University:Engineering Science,2017,51(8):1653-1661(in Chinese).
[7]Guo Xingkuan,Deng Xiaojun,Zeng Jianhong,et al.Analysis and solution to voltage unbalance of the flying capacitor in ZVS three-level DC/DC converter[C].International Telecommunications Energy Conference,2004:684-688.
[8]Sheng Honggang,Wang Fei,Tipton C W.A fault detection and protection scheme for three-level DC-DC converters based on monitoring flying capacitor voltage[J].IEEE Transactions on Power Electronics,2012,27(3):685-697.
[9]Lee I O,Moon G W.Analysis and design of a three-level LLC series resonant converter for high-and wide-inputvoltage applications[J].IEEE Transactions on Power Electronics,2012,27(6):2966-2979.
[10]Li Wuhua,Luo Qingjing,Mei Ye,et al.Flying-capacitor based hybrid LLC converters with input voltage auto-balance ability for high voltage applications[J].IEEE Transactions on Power Electronics,2016,31(3):1908-1920.
[11]Lin Borren,Zhang Shengzhi.Analysis and implementation of a three-level hybrid dc-dc converter with the balanced capacitor voltages[J].IET Power Electronics,2016,9(3):457-465.
[12]周玮阳,虞晓阳,金科,等.半桥三电平直流变换器的电容电压控制策略[J].电工技术学报,2015,30(16):56-62.Zhou Weiyang,Yu Xiaoyang,Jin Ke,et al.Capacitor voltage control strategy for half-bridge three-level converter[J].Transactions of China Eletrotechnical Society,2015,30(16):56-62(in Chinese).
[13]Ruan Xinbo,Wei Jian,Xue Yali,et al.Voltage-sharing of the divided capacitors in non-isolated three-level converters[C].IEEE Applied Power Electronics Conference and Exposition,2004:1725-1729.
[14]Todorovic M H,Palma L,Enjeti P N.Design of a wide input range DC-DC converter with a robust power control scheme suitable for fuel cell power conversion[J].IEEE TransactionsonIndustrialElectronics,2008,55(3):1247-1255.
[15]Yu Xiaoyang,Jin Ke,Liu Zhijun.Capacitor voltage control strategy for half-bridge three-level DC/DC converter[J].IEEE Transactions on Power Electronics,2014,29 (4):1557-1561.

