微电网系统中Tan-Sun坐标变换体系的应用研究
谭广军,孙孝峰
(燕山大学电气工程学院,秦皇岛 066004)
三相电力电子变换器具有能量可双向流动、可实现功率因数控制和对公用电网谐波的抑制等优点,因此已广泛地应用于新能源并网发电[1,2]、交直流混合微电网[3,4]和高压直流输电等系统[5,6]中。然而在实际工况中,由于电网故障、三相负载的不对称性和大功率单相负载的接入等原因,电网电压的不平衡现象是普遍存在的[7-9]。此时,若仍采用传统的控制方法,则将会导致三相电力电子变换器的直流侧电压中叠加偶次电压谐波,无法保证其直流稳压功能,并会使得三相交流电流中产生奇次电流谐波,导致交流电流波形发生畸变,从而降低三相电网的供电质量,甚至会导致变换器运行不稳定,以致停机。
对于三相三线制变换器来说,当电网电压平衡时,通过Clarke变换和Park变换方法可将其三相电流变换为2个不含有二次谐波分量的直流电流,其稳态误差可通过比例积分PI(proportional-integral)控制方法进行补偿。然而当电网电压不平衡时,由于三相电流已不再平衡,因此通过上述坐标变换所得到的直流电流中会出现二次谐波分量,因此PI控制方法就无法实现对电流稳态误差的完全补偿。为此,学者们针对不平衡条件下三相三线制变换器的控制问题开展了研究。
由于三相三线制变换器在两相静止正交坐标系(αβ)下只有2个独立的交流电流,因此一些学者采用Clarke变换将三相电流变换为αβ坐标系下的2个交流电流,并采用比例谐振PR(proportional resonant)控制方法对这2个αβ交流电流进行控制[9-11]。然而,PR控制器的带宽极窄,其对电网频率的细微变化具有极强的敏感性,且只在电网频率处才具有无穷大的增益,因此这将会对电流闭环系统带来稳定性问题。
针对于不含有零序分量的三相不平衡电流,Rioual等提出了正负序同步旋转坐标系(dqp和dqn),其坐标系可将不含有零序分量的三相不平衡电流分解为4个不含有二次谐波的直流电流分量,从而可采用PI控制器对各直流电流分量进行控制[12]。然而,三相电流的正负序dq分量并不能通过坐标变换直接得到,因此通常还需采用陷波器方法对其正负序dq分量进行提取[8,13-14]。
由于正负序dq分量提取方法会带来一定的时间滞后问题,文献[15,16]直接对dqp和dqn坐标系下含有二次谐波分量的4个直流电流信号进行控制,并采用谐振控制方法用来补偿电流的稳态误差。作为谐振控制的替代方法,文献[17,18]采用降阶矢量积分器 ROVI(reduced-order vector integrator)对dqp和dqn坐标系下含有二次谐波分量的4个直流电流信号进行控制。然而,与PR控制方法类似,谐振控制方法和ROVI方法同样也都存在稳定性和可实现性等问题。
为了解决上述坐标变换方法和控制方法中所存在的诸多问题,本文提出了一种新型的Tan-Sun坐标变换体系[19,20],其主要目的是为了将不含有零序分量的三相不平衡交流量直接变换为2个正交等幅的交流量,并通过Park变换可将其进一步变换为2个不含有二次谐波分量的直流量。本文介绍了Tan-Sun坐标变换体系的基本思想,并将其坐标变换体系应用于微电网系统中的三相PWM变换器中,将其数学模型变换到同步旋转dq坐标系下,从而能够采用经典的双闭环PI控制方法对其控制系统进行设计,进而简化其控制系统结构,最后Matlab/Simulink对基于Tan-Sun坐标变换体系的电网电压不平衡条件下的三相PWM变换器分别进行了仿真和实验验证,从而证明了Tan-Sun坐标变换体系在微电网系统中应用的有效性,以及相对于传统的正负序同步旋转坐标变换方法的优越性。
1 Tan-Sun坐标变换体系简介
不含有零序分量的三相不平衡交流量xabc可表示为

式中:φabc为 xabc的初相位;Xm为 xabc的平均幅值,Xm>0,与 xabc的幅值Xabcm具有的关系是

基于式(1)所构建的Tan-Sun坐标变换矩阵为
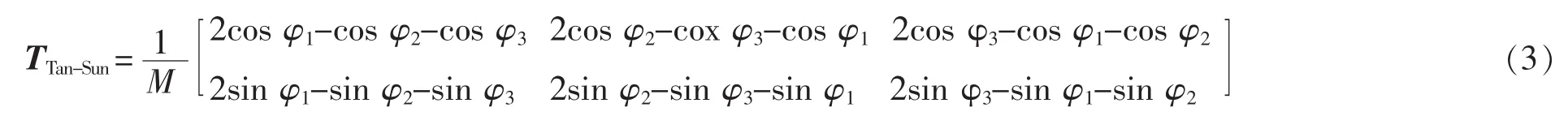

式(3)所示矩阵TTan-Sun可实现从三相不平衡abc静止坐标系到αβ正交静止坐标系的坐标变换过程,即式(1)所示xabc经Tan-Sun变换后可变换为2个具有相同幅值的正交交流量xαβ,再经Park变换后可变换为2个不含有二次谐波分量的直流量xdq。若xabc不含有零序分量,矩阵TTan-Sun可进一步简化为

基于式(1)可得TTan-Sun反坐标变换矩阵为
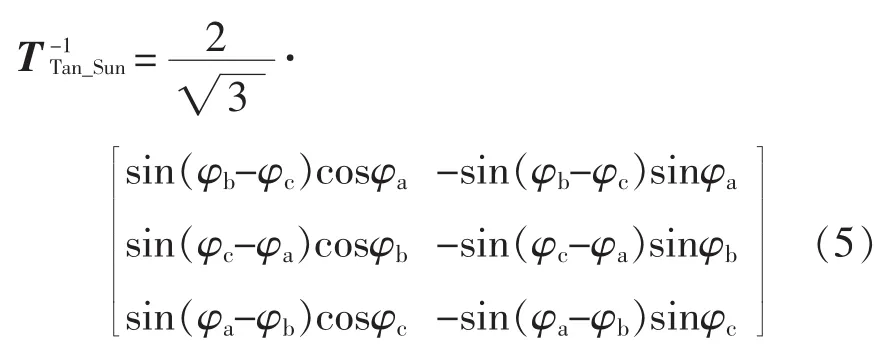
2 基于Tan-Sun坐标变换体系的三相PWM变换器控制系统设计
2.1 三相PWM变换器的数学模型
三相PWM变换器的电路结构如图1所示。

图1 三相PWM变换器电路结构Fig.1 Circuit structure of three-phase PWM converter
图1 中,ea、eb和 ec为三相不平衡电网电压,ia、ib和ic为网侧三相电流,L为三相交流滤波电感,L的寄生电阻记为R,RL为直流负载电阻,C为直流滤波电容,uo为直流输出电压。
若定义某相桥的开关控制信号pk(k∈{a,b,c}),当上桥臂始终导通,下桥臂始终关断时,pk=1,当上桥臂始终关断,下桥臂始终导通时,pk=-1,则pk与占空比sk之间的关系[21]为pk=2sk-1。根据基尔霍夫电压和电流定律可推得三相PWM变换器的数学模型为

三相不平衡交流量xabc的正负序分量之和可表示为xabc与其零序分量之差的形式,即

由于电网电压源采用三线制的连接形式,网侧三相电流iabc的零序分量,因此有

将式(7)代入到式(6)中可得三相PWM变换器的相序分量模型为

从式(9)中可看出,即使电网电压和开关控制信号中均含有零序分量,但并未出现在式(9)中,其零序分量的存在对三相PWM变换器起不到任何作用。因此,三相PWM变换器是一个与零序分量无关的电力电子系统。
2.2 基于Tan-Sun坐标变换体系的数学模型变换
由于三相PWM变换器的被控变量为三相电流,因此Tan-Sun坐标变换体系的建立应基于三相电流定向。针对三相PWM变换器的相序分量模型(9),采用Tan-Sun坐标变换方法可将其数学模型变换到αβ坐标系下,即

采用Park变换方法可将式(10)所示的αβ模型进一步变换到dq坐标系下,即

由于三相电流的自由度个数为2,且式(11)为关于id和iq这2个直流电流的微分方程组,因此Tan-Sun和Park坐标变换方法在dq坐标系下能够实现对三相不平衡电流的直流解耦。
2.3 三相PWM变换器的控制系统设计
三相PWM变换器采用电压外环和电流内环的经典双闭环PI控制系统结构。若要实现单位功率因数控制,电压控制器的输出应作为d轴电流控制器的参考输入,q轴电流控制器的参考输入应设为0。从式(11)中可看出,d轴和q轴模型间存在耦合项-jωLidq,通过电流前馈解耦方法可实现dq轴模型之间的解耦。
需要注意的是,由于Tan-Sun坐标变换方法是基于三相电流定向的,edq中通常会含有二次谐波分量,因此必须要在电流内环增加edq的前馈环节以消除其谐波影响。通过上述分析可得pdq的控制律为
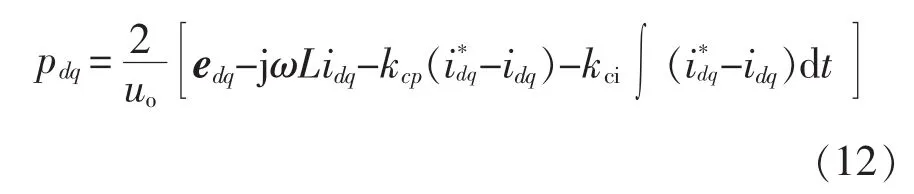
式中:kcp为电流控制器的比例系数,V·A-1;kci为电流控制器的积分系数,V·(A·s)-1。
在电网电压不平衡条件下,基于Tan-Sun坐标变换体系的三相PWM变换器的总体控制系统结构如图2所示。
图2中,φiabc的取值应维持直流输出电压稳定以及单位功率因数控制,由文献[13]可知,为了实现上述这两个控制目标,关于正负序dq坐标系下4个参考电流的控制律应设为

图2 基于Tan-Sun坐标变换体系的三相PWM变换器总体控制结构Fig.2 Overall control structure of three-phase PWM converter based on Tan-Sun coordinate transformation system


pa1、pb1和 pc1为 pα和pβ经 Tan-Sun 反变换直接得到的调制信号,再经SVPWM模块后可变换为三相开关控制信号 pa、pb和 pc。
3 仿真结果分析
本节将采用Matlab/Simulink软件,对电网电压不平衡条件下基于Tan-Sun坐标变换体系的三相PWM变换器进行仿真验证,其仿真参数如表1所示。

表1 系统仿真参数Tab.1 Parameters in system simulation
三相电网电压eabc分别设为

根据国家标准GB/T 15543-2008《电能质量 三相电压不平衡》,由式(15)可计算得出负序电压不平衡度为16.37%。
若基于三相电流定向建立Tan-Sun坐标变换体系,其三相电流稳态仿真波形如图3所示。
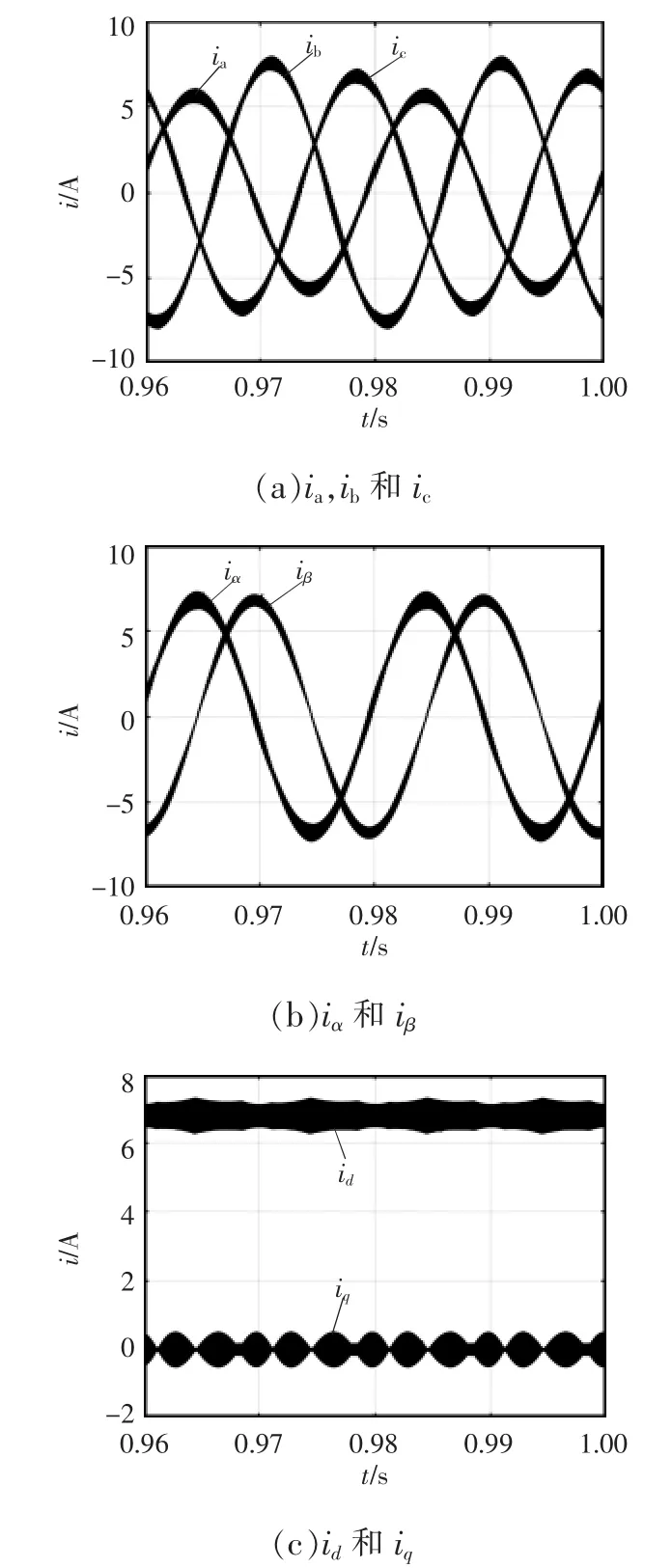
图3 三相电流稳态仿真波形Fig.3 Simulation waveforms of three-phase currents in steady state
图3(a)中的三相不平衡电流 ia、ib和 ic经 Tan-Sun变换后得到图3(b)中的2个正交等幅的交流电流 iα和 iβ,再经 Park 变换得到图3(c)中的 2 个不含有二次谐波分量的直流电流id和iq,因此验证了Tan-Sun坐标变换体系的正确性和有效性。
为了验证Tan-Sun坐标变换体系在三相PWM变换器中的动态响应性能,在如下3种不同的情况下进行了测试:①ec的电压有效值从90 V跌落到45 V;②电网频率从50 Hz跌落到45 Hz;③负载电阻从100 Ω突增到200 Ω。上述3种暂态情况的仿真波形分别如图4~图6所示。
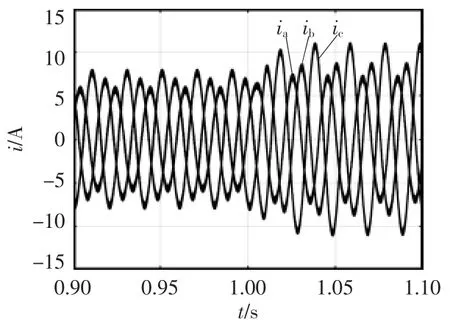
图4 ec有效值变化时的三相电流仿真波形Fig.4 Simulation waveforms of three-phase currents when RMS value of ecchanges

图5 电网频率变化时的三相电流仿真波形Fig.5 Simulation waveforms of three-phase currents when grid frequency changes

图6 负载电阻变化时的三相电流和直流电压仿真波形Fig.6 Simulation waveforms of three-phase currents and DC voltage when load resistance changes
图6中的直流输出电压出现一个10 V的动态上升,并于50 ms内回复稳定状态。从图4~图6可看出,当三相PWM变换器中出现扰动时,Tan-Sun坐标变换体系仍能实现对三相PWM变换器的有效控制,三相电流的动态响应速度很快,因此Tan-Sun坐标变换体系具有良好的动态响应特性。
为了证明Tan-Sun坐标变换体系相对于正负序同步旋转坐标系的优越性,基于三相PWM变换器对这2种坐标变换体系进行了仿真对比。由于这2种坐标变换体系对电压控制环起不到任何作用,因此仿真过程只采用电流控制环。为了验证这2种坐标变换体系的响应特性,Tan-Sun坐标变换体系的d轴参考电流分别设置为从3 A变化到6 A和从6 A变化到3 A,q轴参考电流设置为0,所对应的正负序同步旋转坐标系的正负序dq参考电流可根据d轴参考电流进行设置,以保证这2个坐标变换体系的参考电流是相同的。这2种坐标变换体系的dq轴电流仿真波形分别如图7和图8所示。

图7 d轴参考电流变化时采用Tan-Sun坐标变换体系的dq轴电流仿真波形Fig.7 Simulation waveforms of idqusing Tan-Sun coordinate transformation system whenhas step changes

图8 d轴参考电流变化时采用正负序同步旋转坐标系的dq轴电流仿真波形Fig.8 Simulation waveforms of idqby using PNS synchronous rotating coordinate systems when has step changes
图8中,采用正负序同步旋转坐标系的dq轴电流波形是通过基于正负序dq参考电流定向的Tan-Sun坐标变换体系得到的。从图7和图8中可看出,采用Tan-Sun坐标变换体系的dq轴电流的响应速度要远快于采用正负序同步旋转坐标系的dq轴电流,因此相对于正负序同步旋转坐标系,Tan-Sun坐标变换体系能够提高电流环的带宽,并能够进一步提高三相不平衡PWM变换器的控制性能。
4 实验验证
实验室搭建了三相PWM变换器实验平台,由三相桥式主电路、三相可编程交流电源、主控板及负载构成。三相可编程交流电源为Chroma model 61704,主要用来模拟三相不平衡电压;主控板为以TI公司的数字信号控制器TMS320F28335为主控芯片的数字控制器,包含有辅助电源、采样电路、调理电路、驱动电路及保护电路等;负载由2个200 Ω/5 kW的电阻并联构成,实验平台如图9所示。

图9 实验平台Fig.9 Experimental platform
三相可编程交流电源设置为式(15)所示的三相不平衡电压。软件采用C语言编程,主要包含以下两个部分:主程序和中断子程序。主程序主要包含系统初始化、外设资源配置等设置,中断子程序是系统控制的核心,包括AD采样值读取及数据处理程序,坐标变换、电压电流控制以及SVPWM调制,DA输出变量观测程序等。采用PWM定时中断的形式,中断频率10 kHz,也就是PWM变换器的开关频率。
为了验证Tan-Sun坐标变换体系在三相PWM变换器应用中的有效性,在三相PWM变换器平台上进行了实物实验,其稳态电流波形如图10所示。
图10(a)中的 ia、ib和 ic是不平衡的,图10(b)中的 iα和iβ是正交等幅的,图10 (c)中的 id和iq均是不含有二次谐波分量的直流量,因此验证了Tan-Sun坐标变换体系的正确性。

图10 三相电流的稳态实验波形Fig.10 Experimental waveforms of three-phase currents in steady-state
为了验证Tan-Sun坐标变换体系在三相PWM变换器中的动态响应性能,实物实验分别在ec有效值、电网频率和负载电阻发生变化时进行了验证,所对应的实验波形分别如图11~图13所示。
图11中,由于ec有效值发生了跌落,ic的幅值增加的最多。图13中的直流输出电压有一个很小的动态上升,且在30 ms内恢复到稳定状态。从图11~图13中可看出,在系统出现扰动时,Tan-Sun坐标变换体系仍然能够正常工作,且电流环具有很高的控制带宽。

图11 ec有效值变化时的三相电流实验波形Fig.11 Experimental waveforms of three-phase currents when the RMS value of ecchanges

图12 电网频率变化时的三相电流实验波形Fig.12 Experimental waveforms of three-phase currents when grid frequency changes

图13 负载电阻变化时的三相电流和直流电压实验波形Fig.13 Experimental waveforms of three-phase currents and DC voltage when load resistance changes
最后给出Tan-Sun坐标变换体系和正负序同步旋转坐标系在三相PWM变换器中应用的对比实验波形,采用这2种坐标变换体系的dq轴电流波形分别如图14和图15所示。

图14 d轴参考电流变化时采用Tan-Sun坐标变换体系的dq轴电流实验波形Fig.14 Experimental waveforms of idqby using Tan-Sun coordinate transformation system when has step changes

图15 d轴参考电流变化时采用正负序同步旋转坐标系的dq轴电流实验波形Fig.15 Experimentalwaveformsofidqusing positiveand negative-sequence synchronous rotating coordinate systems when has step changes
从图14和图15中可清晰看出,采用Tan-Sun坐标变换体系的dq轴电流响应速度要远高于采用正负序同步旋转坐标系的dq轴电流响应速度,因此相对于正负序同步旋转坐标系,Tan-Sun坐标变换体系能够提高三相不平衡PWM变换器的控制性能,且更适用于控制三相不平衡电力电子系统。
5 结语
本文介绍了一种新型的Tan-Sun坐标变换体系,其能够将不含有零序分量的三相不平衡交流量直接变换为2个正交等幅的交流量,再经Park变换可将其进一步变换为2个不含有二次谐波分量的直流量,从而简化了对三相不平衡交流量的分析和设计过程。基于Tan-Sun坐标变换体系所具有的上述优点,本文将其体系理论应用于电网电压不平衡条件下的微电网变换器模型变换过程中,并将其数学模型变换到同步旋转dq坐标系下,从而可采用经典双闭环PI控制方法对其实现有效控制,并通过仿真和实物实验验证了Tan-Sun坐标变换体系的有效性,以及对于系统扰动的鲁棒性。通过仿真和实验结果还可得出,相对于传统的正负序同步旋转坐标变换体系,Tan-Sun坐标变换体系能够提高电流环的带宽,从而有利于提高三相不平衡PWM变换器的控制性能。
参考文献:
[1]Camacho A,Castilla M,Miret J,et al.Active and reactive power strategies with peak current limitation for distributed generation inverters during unbalanced grid faults[J].IEEE Transactions on Industrial Electronics,2015,62(3):1515-1525.
[2]Kabiri R,Holmes D G,Mcgrath B P.Control of active and reactive power ripple to mitigate unbalanced grid voltages[J].IEEE Transactions on Industry Applications,2016,52(2):1660-1668.
[3]Zhu Minglin,Hang Lijun,Li Guojie,et al.Protected control method for power conversion interface under unbalanced operating conditions in AC/DC hybrid distributed grid[J].IEEE Transactions on Energy Conversion,2016,31(1):57-68.
[4]王晓声,孙凯,李运帷.交直流混合微网中双向接口变换器控制综述[J].电源学报,2016,14(2):70-79.Wang Xiaosheng,Sun Kai,Li Yunwei.Review of control strategies for bidirectional interfacing converters in hybrid AC/DC microgrid[J].Journal of Power Supply,2016,14(2):70-79(in Chinese).
[5]Moon J W,Park J W,Kang D W,et al.A control method of HVDC-modular multilevel converter based on arm current under the unbalanced voltage condition[J].IEEE Transactions on Power Delivery,2015,30(2):529-536.
[6]Li Shaohua,Wang Xiuli,Yao Zhiqing,et al.Circulating current suppressing strategy for MMC-HVDC based on nonideal proportional resonant controllers under unbalanced grid conditions[J].IEEE Transactions on Power Electronics,2015,30(1):387-397.
[7]Stankovic A V,Chen K.A new control method for inputoutput harmonic elimination of the PWM boost-type rectifier under extreme unbalanced operating conditions[J].IEEE Transactions on Industrial Electronics,2009,56(7):2420-2430.
[8]Yin Bo,Oruganti R,Panda S K,et al.An output-powercontrol strategy for a three-phase PWM rectifier under unbalanced supply conditions[J].IEEE Transactions on Industrial Electronics,2008,55(5):2140-2151.
[9]Roiu D,Bojoi R I,Limongi L R,et al.New stationary frame control scheme for three-phase PWM rectifiers under unbalanced voltage dips conditions[J].IEEE Transactions on Industry Applications,2010,46(1):268-277.
[10]Li Zixin,Li Yaohua,Wang Ping,et al.Control of threephase boost-type PWM rectifier in stationary frame under unbalanced input voltage[J].IEEE Transactions on Power Electronics,2010,25(10):2521-2530.
[11]Mirhosseini M,Pou J,Karanayil B,et al.Resonant versus conventional controllers in grid-connected photovoltaic power plants under unbalanced grid voltages[J].IEEE Transactions on Sustainable Energy,2016,7(3):1124-1132.
[12]Rioual P,Pouliquen H,Louis J P.Regulation of a PWM rectifier in the unbalanced network state using a generalized model[J].IEEE Transactions on Power Electronics,1996,11(3):495-502.
[13]Song H S,Nam K.Dual current control scheme for PWM converter under unbalanced input voltage conditions[J].IEEE transactions on Industrial Electronics,1999,46(5):953-959.
[14]Yazdani A,Iravani R.A unified dynamic model and control for the voltage-sourced converter under unbalanced grid conditions[J].IEEE Transactions on Power delivery,2006,21(3):1620-1629.
[15]Suh Y,Lipo T A.Control scheme in hybrid synchronous stationary frame for PWM AC/DC converter under generalized unbalanced operating conditions[J].IEEE Transactions on Industry Applications,2006,42(3):825-835.
[16]Suh Y,Lipo T A.Modeling and analysis of instantaneous active and reactive power for PWM AC/DC converter under generalized unbalanced network[J].IEEE Transactions on Power Delivery,2006,21(3):1530-1540.
[17]Nian Heng,Cheng Peng,Zhu Z Q.Coordinated direct power control of DFIG system without phase-locked loop under unbalanced grid voltage conditions[J].IEEE Transactions on Power Electronics,2016,31(4):2905-2918.
[18]Cheng Peng,Nian Heng.Direct power control of voltage source inverter in a virtual synchronous reference frame during frequency variation and network unbalance[J].IET Power Electronics,2016,9(3):502-511.
[19]Tan Guangjun,Cheng Jie,Sun Xiaofeng.Tan-Sun coordinate transformation system theory and applications for three-phase unbalanced power systems[J].IEEE Transactions on Power Electronics,2017,32(9):7352-7380.
[20]Tan Guangjun,Sun Xiaofeng.Analysis of Tan-Sun coordinate transformation system for three-phase unbalanced power system[J].IEEE Transactions on Power Electronics,2018,33(6):5386-5400.
[21]Lee T S.Lagrangian modeling and passivity-based control of three-phase AC/DC voltage-source converters[J].IEEE Transactions on Industrial Electronics,2004,51(4):892-902.

