基于三阶广义积分器的谐波检测算法

武 健，张彩红，王 蕊，漆 岳，尤燕飞，徐殿国

（哈尔滨工业大学电气工程及自动化学院，哈尔滨150006）

近年来，作为集中式发电的有效补充，分布式发电技术及并网系统已日趋成熟。随着单位千瓦电能生产价格的不断下降，分布式发电正得到越来越广泛的应用。同时，分布式电源并网带来的复杂的谐波谐振问题受到越来越多的关注[1]。分布式能源发电采用的并网逆变器属于电力电子设备，越来越多电力电子设备的应用，会对配电网注入大量谐波，造成了日益严重的谐波污染。相比于传统电网，微网和主动配电网系统的谐波现象呈现出新的特点。

为解决逆变器并网带来的谐波问题，需要在并网逆变器与电网之间加设滤波装置。传统的LCL滤波器对于高频谐波电流表现出很大阻抗，但对于某些特定频次的谐波表现出的阻抗很小，这些特定频次的谐波电流不但不会被抑制，反而会被LCL滤波器放大[2-4]。传统无源阻尼方法，如在LCL滤波器电容支路串联阻尼电阻，增加了滤波器在谐振频率处的阻尼，在一定程度上抑制了谐振的发生。但引入的无源阻尼电阻引起变换器发热，带来了额外损耗。近年来，相关学者提出有源阻尼的方法，在电网公共点连接有源阻尼器，通过控制算法来增加系统的等效阻尼，实现谐振抑制。由于该方法不增加耗能元件，因此不存在阻尼损耗问题。有源阻尼器值只工作在谐振频率处，因此对当前电网中谐波的检测变得尤其重要，检测精度直接影响有源阻尼器的作用效果。

目前对广义谐波电流的检测方法都是以瞬时无功理论为基础，但多个滤波器的引入，会引起相位滞后的问题。文献［5］提出一种运用双向解耦法消除复数分量中的谐波电流，虽没有采用低通滤波器，但是算法过于复杂，而且多个双向解耦装置的加入减慢了系统动态响应速度；文献［6］提出基于平均值理论的自适应锁相环法，用积分均值代替低通滤波器，自适应锁频环实时检测电网频率，提高了检测的实时性，但是没有考虑到频率波动和电压三相不平衡对检测算法的影响。文献[7]运用二阶广义积分器 SOGI（second order generalized integrator），实现了基波正序分量的提取，但无法消除谐波对检测精度的影响；文献[8]提出了由多个二阶广义积分器与锁相环MSOGI-FLL（multi second-order generalized integrator-phase locked loop）组成的谐波检测算法，该方法基于锁相环FLL和二阶广义积分器，将多个二阶广义积分器并联，实现检测电网电压基波正负序分量，以及谐波的正负序分量，由于FLL的存在，系统可以实现频率自适应。但该系统不能再次谐波和简谐波干扰下，不能保证检测精度；文献[9]提出了级联型二阶广义积分器的结构，克服了次谐波和间谐波影响，但多畸变电网下的直流偏置问题仍无法解决。

因此，本文提出一种基于三阶广义积分控制器TOGI（third-order generalized integrator）的谐波检测算法，该方案通过采用多个基于三阶广义积分的正交信号发生器构成的反馈网络，消除直流偏移对检测结果的影响，提高检测精度。通过消除特定次谐波，同步提取精度更高的电压和电流的正负序基波分量，同时能够自适应跟踪电网角频率。在输入信号畸变严重且含有直流偏置情况下，仍然可以实现高精度检测结果。仿真结果说明在畸变电网下应用该算法效果显著。

1 基于二阶广义积分器的谐波检测实现及存在的问题

1.1 谐波检测原理

SOGI具有陷波特性，只允许频率为ω0的交流分量通过。图1所示为SOGI的结构，其中ξ是系统阻尼系数。FLL输入信号是SOGI提供的正交信号vq与偏差信号e，根据两路输入信号的频率特性，进而通过带有负增益的积分器，实现对角频率的跟踪，输出的预估频率ω0提供给SOGI，通过不断调整SOGI输入的频率ω0，直至误差角频率为0，这样就实现了二阶广义积分器的自适应锁定角频率的功能。

SOGI输出信号vd与输入信号vin同相位，vq与vin相位差为90°，vd与vq互为一组正交信号。从输入输出特性分析，SOGI对vd表现带通特性，而对vq表现为低通特性。其闭环传递函数为

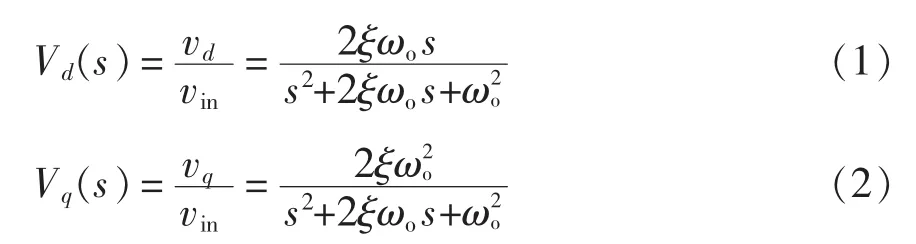
式中，ωo为SOGI的输入频率。

MSOGI-FLL结构如图2所示。多个SOGI并联，通过交叉反馈消除谐波对基波电压的影响，可以从畸变电网中提取出基波正负序分量以及谐波分量。该结构不仅可以提取基波及谐波的幅值和频率，同时可以实现给定信号的正负序分离。

图1 SOGI-FLL结构Fig.1 Structure of SOGI-FLL

1.2 直流偏置对谐波检测系统的影响

直流偏置现象对MSOGI-FLL的检测精度存在很大影响。在Simulink中搭建MSOGI-FLL模型，模型设计为检测3次、5次和7次谐波。取ξ=0.707，γ=50，输入电压为 vin=50 V，fo=50 Hz，在 t=0.5 s时刻，电网电压出现畸变，直流偏置电压V0=10 V。

图2 MSOGI-FLL结构Fig.2 Structure of MSOGI-FLL

图3所示为0.5 s处发生10 V直流偏置，FLL输出预估频率 ω0。由图可以看出，当 0＜t＜0.5 s时，锁频环FLL输出角频率稳定在ω0=314 rad/s，t＞0.5 s后，FLL输出波形振荡。当直流偏置电压V0=10 V时，输出角频率振荡幅值约为15 rad/s。角频率输出不稳定，严重影响SOGI输出特性。

图3 MSOGI-FLL系统输出角频率响应Fig.3 Angular frequency response of MSOGI-FLL output with a 10 V DC-offset at 0.5 s

2 三阶广义积分器谐波检测算法

2.1 三阶广义积分器原理

本文提出一种基于三阶广义积分器的谐波检测算法来解决直流偏置电压对谐波检测精度的影响。三阶广义积分器结构如图4所示。

图4中，输入信号为给定信号vin（t）和频率值ω0，输出信号分别为 v1（t）、v2（t）、v3（t），则输出信号与输入信号的关系分别用闭环传递函数表示为

图4 三阶广义积分器结构Fig.4 Structure of TOGI

式中，vin（s）、v1（s）、v2（s）、v3（s）分别为信号 vin（t）、v1（t）、v2（t）、v3（t）的拉普拉斯变换。

假设输入信号是含有直流偏移分量的正弦信号，即

式中，vin（t）为输入电压信号；v0为直流分量；vc、ωc和φc分别为交流分量的幅值、频率和相位。

由文献[10]可知，TOGI的输出信号分别为

式中，k为常数。

由此可以看出，输出信号v1（t）不含有直流分量，主要归因于其传递函数分子中的一阶微分项，其交流项与输入信号交流分量同幅同相；v2（t）含有直流分量，其交流分量与输入信号同幅，相位滞后90°；v3（t）仅含直流分量。

2.2 MTOGI-FLL工作原理

由上述分析可知，频率锁定环节输出在电网电压发生直流偏置时发生畸变，主要原因是其输入信号v2（t）中含有直流分量；同时因为系统中没有直流反馈，电网发生直流偏置畸变时，给定信号与实际输出的偏差信号e（t）受直流偏置影响不能稳定到 0，即偏差信号 e（t）中也含有直流分量；v2（t）-v3（t）与 v1（t）项同幅，相位滞后其 90°，为了消除频率锁定环节输入信号中直流分量影响，将 v2（t）-v3（t）项作为频率锁定环节FLL的输入；将TOGI输出信号 e（t）与 v3（t）作差，抵消直流偏置对锁频转置的影响，即将 e（t）-v3（t）作为 FLL 的另一输入信号，从而使频率锁定环节输入信号完全不受直流偏置的影响，实现角频率自适应稳定输出。基于TOGI的滤波结构TOGI-FLL结构如图5所示。

图5 TOGI-FLL结构Fig.5 Structure of TOGI-FLL

可见，TOGI能够抑制输入信号中的直流分量对系统的影响，产生与系统输入基波分量同频同幅的两相正交信号。

由三阶广义积分器构成谐波检测反馈网络，则第i次谐波输出为

式中：i、j为谐波次数；vi为各次谐波输出；Vi（t）为第 i次谐波的传递函数。

进一步整理可得

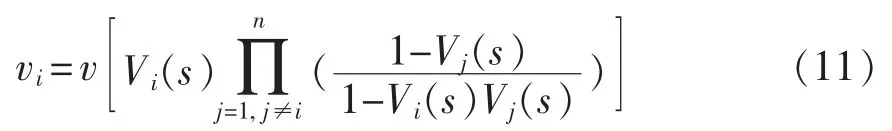
图6给出了取i=1，j=3、5、7时，系统基波传递函数bode图。由频率响应可以看出，系统在f=50 Hz处增益为1，可保证基波无障碍通过；在f=150、250、350 Hz处均有幅值很大的负增益，使3次、5次、7次谐波得到很大削减，保证基波准确输出。

在Matlab/Simulink搭建单相检测模型，参数设置为 ξ=0.707， γ=50， 输入电压为 vin=50 V，fo=50 Hz。设置在t=0.5 s时刻，电网电压出现畸变，直流偏置电压v0=10 V。MTOGI-FLL系统设置为检测基波电压与3次、5次、7次谐波电压。角频率输出响应如图7所示。

对比图3与图7可以看出，基于二阶广义积分的谐波检测系统，在t=0.5 s电网发生畸变后，FLL输出角频率振荡，幅值约为15 rad/s；而改进后的谐波检测系统，FLL输出可以在0.1 s内恢复到交流给定频率，并维持稳定输出，频率锁定环节性能得到显著改善。

图6 MTOGI-FLL基波频率响应Fig.6 Fundamental wave frequency response of MTOGI-FLL

图7 MTOGI-FLL系统输出角频率响应Fig.7 Angular frequency response of MTOGI-FLL output

3 实验仿真

3.1 单相谐波检测环节仿真

在Matlab中搭建单相谐波检测模型，参数设置为 ξ=0.707，γ=50，输入电压为 vin=50 V，fo=50 Hz。在t=0.5 s电网电压发生畸变，出现3次、5次、7次谐波，谐波电压幅值均为10 V，直流偏置电压v0=10 V。电网电压波形如图8所示。MTOGI-FLL谐波检测系统设置为检测基波电压与3次、5次、7次谐波电压，基波与谐波电压检测结果如图9所示。

图8 单相系统电网电压仿真波形Fig.8 Grid voltage waveform of single-phase simulation system

3.2 三相谐波检测环节仿真

搭建三相谐波检测模型，参数设置为ξ=0.707，γ=50，输入电压为 vin=50 V，fo=50 Hz。在 t=0.5 s时电网发生畸变，出现5次正序分量和7次谐波负序分量，直流偏置电压v0=10 V。电网电压波形如图10所示。MTOGI-FLL谐波检测系统设置为检测基波正、负序电压与3次、5次、7次谐波正、负序电压，基波与谐波电压检测结果如图11所示。

由仿真结果可以看出，基波正序分量、5次谐波正序分量和7次谐波负序分量检测结果准确；基波负序分量、5次谐波负序分量和7次谐波正序分量经过暂态后恢复到0。

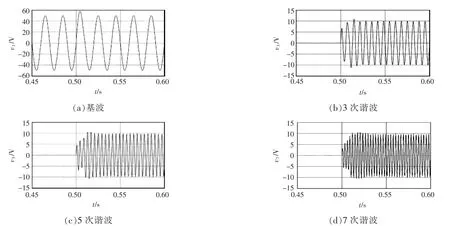
图9 单相系统谐波检测仿真结果Fig.9 Harmonic detection results of single-phase simulation system

图10 三相系统电网电压Fig.10 Grid voltage of three-phase simulation system

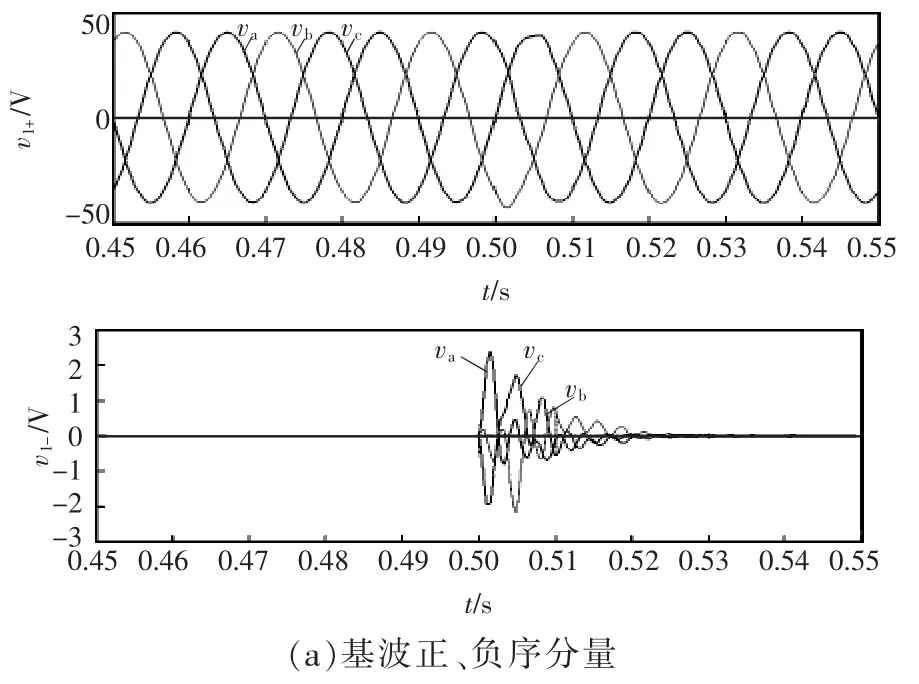
图11 三相系统谐波检测仿真结果Fig.11 Harmonic detection results of three-phase simulation system

4 结论

（1）在谐波检测系统中引入三阶广义积分，利用其输出特性，可以消除直流偏置对频率锁定环节FLL的影响，解决畸变电网下FLL不能稳定输出的问题，保证频率锁定环节的稳定输出。

（2）由多个三阶广义积分器与频率锁定环节交叉反馈构成的MTOGI-FLL系统，可以实现基波与特定次谐波的检测，通过交叉反馈网络提高检测精度，消除直流偏置对谐波检测结果的影响。

（3）由单相和三相仿真结果证明了提出的基于三阶广义积分器的MTOGI-FLL系统在直流偏置畸变电网下的优良性能。

参考文献：

1]王成山,李鹏.分布式发电、微网与智能配电网的发展与挑战[J].电力系统自动化,2010,34（2）:10-14.Wang Chengshan,Li Peng.Development and challenges of distributed generation,the micro-grid and smart distribution system[J].Automation of Electric Power System,2010,34（2）:10-14（in Chinese）.

[2]刘计龙,马伟明,肖飞.一种LCL滤波器有源阻尼策略与设计方法[J].电机与控制学报,2013,17（5）:22-27.Liu Jilong,Ma Weiming,Xiao Fei.An active damping control strategy and design method for LCL filter[J].Electric Machines and Control,2013,17（5）:22-27（in Chinese）.

[3]刘飞,查晓明,段善旭.三相并网逆变器LCL滤波器的参数设计与研究[J].电工技术学报,2010,25（3）:110-116.Liu Fei,Zha Xiaoming,Duan Shanxu．Design and research on parameter of LCL filter in three-phase grid-connected inverter[J].Transactions of China Electrotechnical Society,2010,25（3）:110-116（in Chinese）.

[4]阚加荣,谢少军,刘爱忠.逆变器单元用LCL滤波器的并联系统性能分析 [J].电机与控制学报,2010,14（2）:90-98.Kan Jiarong,Xie Shaojun,Liu Aizhong.Performance analysis of parallel system using LCL filter inverter unit[J].Electric Machines and Control,2010,14（2）:90-98（in Chinese）.

[5]Abulanwar S,Chen Zhe,Iov F.Improved FRT control scheme for DFIG wind turbine connected to a weak grid［C］//5th IEEE PES Asia-Pacific Power and Energy Engineering Conference.Kowloon,China,2013:1-6.

[6]Wang Liang,Jiang Qirong,Hong Lucheng,et al.A novel phase-locked loop based on frequency detector and initial phase angle detector[J].IEEE Transactions on Power Electronics,2013,28（10）:4538-4549

[7]Vazquez S,Sanchez J A,Reyes M R,et al.Adaptive vectorial filter for grid synchronization of power converters under unbalanced and/or distorted grid conditions[J].IEEE Transactions on Industrial Electronics,2014,61（3）:1355-1367.

[8]Wang Xiongfei,Blaabjerg F,Liserre M.An active damper to suppress multiple resonances with unknown frequencies[C].2014 IEEE Applied Power Electronics Conference and Exposition.Fort Worth,USA,2014:2184-2191.

[9]Matas J,Castilla M,Miret J,et al.An adaptive prefiltering method to improve the speed/accuracy tradeoff of voltage sequence detection methods under adverse grid conditions[J].IEEE Transactions on Industrial Electronics,2014,61（5）:2139-2151.

[10]Fedele G,Ferrise A,Muraca P.An adaptive quasi-notch filter for a biased sinusoidal signal estimation[C]//9th IEEE International Conference on Control and Automation （ICCA）.Santiago,Chile,2011:1060-1065.