注入式有源谐波电阻谐振抑制方法
聂 程 ,王 跃 ,雷万钧 ,李 甜 ,许嘉沄
(1.西安交通大学电气工程学院,西安 710049;2.上海船舶设备研究所,上海200031)
配电网是连接输电网和终端电力用户的重要网络,在电力系统中承担着电能传输和分配的任务。对功率因数偏低的配网进行合理的无功补偿,可以给电网的安全性和经济性都能带来极大的好处[1]。对于10 kV等级的配电网,补偿无功的方式一般有两种:无源补偿和有源补偿。有源补偿方式,如链式STATCOM[1,2],动态性能优越,但成本高,控制复杂;无源补偿方式,如并联电力电容,补偿容量大且安装方便,维护简单,成本低。目前并联电力电容器的补偿方式是中压配网应用最为广泛的补偿方式,但是无源补偿方式使用的电容可能和电网线路之间产生谐振[3]。
确定配电网谐振频率是选择阻尼方案的基础。目前电力系统中计算谐振频率的方法主要有解析法、频谱分析法、模态分析法[4-7]等。前两种方法计算比较复杂,需要分析计算各节点的阻抗得到相应的频域信息,进而确定系统的谐振信息。而模态分析法具有高效方便的优点,只通过对节点导纳矩阵的处理即可得到全部的谐振频率[4,5]。更重要的是,模态分析法可以得到比解析法和频谱法更多的信息[6,7],可以为谐振抑制提供参考。
配电网谐振抑制的方法主要分为无源方式和有源方式[8,9]。无源方式多指通过在无功补偿电容上串联无源器件如电感器或电阻器来实现抑制谐振放大的目的。有源方式利用电力电子变流器实现阻尼,具有更好的动态性能,且避免了能量损耗,是近年来配电网阻尼抑制研究的热点。R-APF方式可以有效地抑制谐波谐振,但是由于变流器需要直接和电网并联,变流器需要承受全部的基波电压,因此不适合用于中压配电网,且大容量与高动态特性之间的矛盾给变流器设计带来困难[10,11]。混合滤波有效地降低了变流器所需承受的端口电压,且不需要额外的电源[12-14],但是增加了无功补偿电容中的谐波电流,引起发热等问题。文献[15]利用PWM变流器在谐波频率上模拟电阻特性,利用有源谐波电阻AHR(active harmonic resistance)实现阻尼谐振的目的。有源谐波电阻不需要承担基波电压或电流,进一步降低了阻尼对变流器容量的需求,更加适合用于中压配电网,但是对于谐波电阻取值,阻抗特性等方面缺乏深入的研究分析。
本文利用谐振模态分析法确定中压配电网系统的谐振频率,基于注入式的结构建立电压控制电流型有源谐波电阻的阻抗模型,进而根据谐振频率确定最优的等效谐波电阻阻值。仿真和实验结果证实本文提出的有源谐波电阻对于抑制谐振放大的有效性。
1 中压配网系统谐振分析
1.1 谐振模态分析法
谐振模态分析法是研究电力系统谐振问题的一种有效工具,它通过解耦的方式把复杂的谐振现象分解成若干简单的关键模型,并且可以在得到系统潜在谐振频率的同时,分析各节点受到谐振电压的影响程度。在配电网中,各支路一般都是并联在交流母线上。无源支路一般由补偿电容和串联电感构成,通过分析串联电感受到谐振电压的影响,即可得到无功补偿支路的电流谐振情况。根据文献[16],系统的节点导纳矩阵可以分解为

式中:Λ为对角矩阵,表示导纳矩阵的特征根;L和T分别为左、右特征向量矩阵,且满足L=T-1。特征根的倒数具有电阻的单位,所以定义为系统的模态阻抗。T矩阵的行元素是各节点电流作为激励源时对谐振的激励作用强弱,而L矩阵的列元素是各节点受到谐振电压的大小。
1.2 中压配电网算例模型
工业大型负载诸如电弧炉,运行产生大量的无功和谐波。使其并联的无功补偿电容和电网发生谐振。以10 kV配网为例,图1为含有感性非线性负载的中压配电网单相示意。

图1 10 kV中压配电网单相示意Fig.1 Schematic of single-phase circuit of 10 kV middle-voltage distribution network
图1的配电网中,包含有线路阻抗LS、LS1,末端连接感性非线性负载,电容器C及串联电感L采用就近补偿方式。节点①处引出,可能连接有其他负载,用于考察非线性负载谐波对10 kV母线上其他并联负载的影响。其电路参数见表1所示。

表1 中压配网电路参数Tab.1 Parameters of the system in middle-voltage distribute network
考虑到电网中所有负载的端电压均由电网电压确定,所以可以近似将负载等效为电流源。利用模态分析法得到系统的模态阻抗,如图2所示。

图2 10 kV中压配电网模态阻抗Fig.2 Modal impedance of the 10 kV middle-voltage distribution network

参考L矩阵第3列的元素,节点③处会承受很大的谐振电压,且节点①处的谐振电压高于节点②处的谐振电压。同理,由T矩阵第3行元素可以看出,节点②处注入较小的谐波电流即可以引起严重的谐振。
为了验证模态分析的结果,根据算例参数得到系统中各节点电压和支路电流仿真波形,分别如图3和图4所示。
仿真结果中,节点③电压和无功补偿支路电流中7次谐波成分含量很大。

图3 节点电压波形Fig.3 Waveforms of nodal voltages

图4 支路电流波形Fig.4 Waveforms of branch currents
2 基于注入式有源谐波电阻思想的谐振抑制方法
基于有源谐波电阻[11]的思想,本文提出一种受控电流源型的有源谐波电阻控制方式,如图5所示。图5(a)中AHR以注入式的结构接入10 kV配电网,由于无功补偿电容C的分压和串联电感L的分流,AHR变流器仅承受很小的基波电压和基波电流。
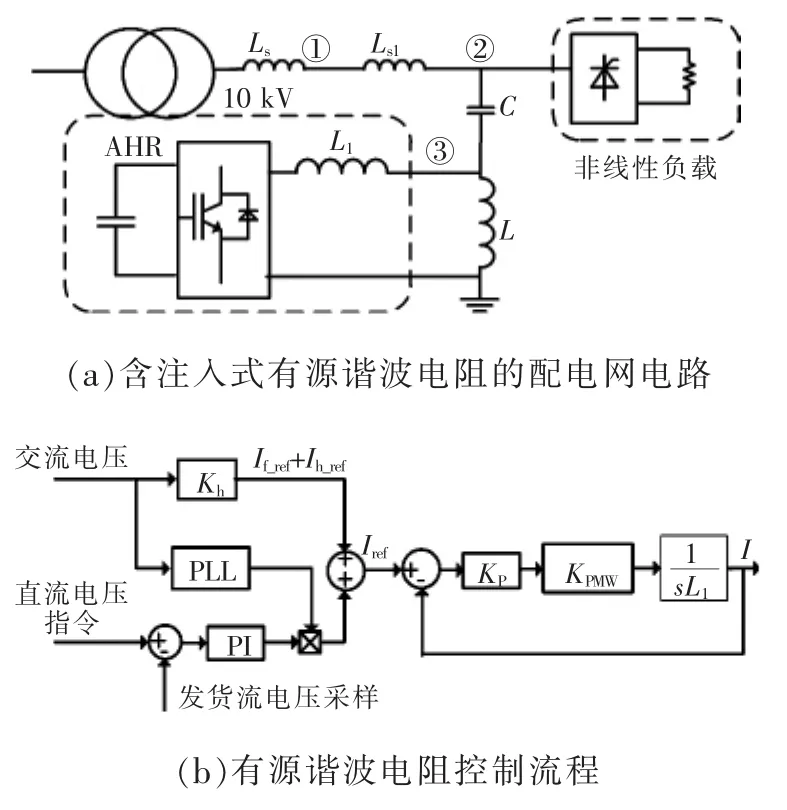
图5 电压控制电流型有源谐波电阻Fig.5 Active harmonic resistance in voltage-controlledcurrent mode
从图5(b)的控制流程可见,变流器的输出电流指令的上半部分用于控制变流器模拟电阻的特性,下半部分用于稳定变流器的直流侧电压。其中谐波电流指令由变流器交流电压直接生成,这种方式避免了谐波所导致的延时,使得有源谐波电阻具有更好的动态性能。合成效果使得变流器呈现谐波电阻特性,即

式中:Kh为等效的谐波电阻;uh和ih分别为变流器端口谐波电压和谐波电流。
忽略变流器损耗,在谐波段吸收有功能量,在基波频率上向电网回馈有功能量。谐波电流输出I到谐波电流给定Iref的闭环传递函数为

式中,Tc(s)为电流开环传递函数,表示为

式中:Kp(s)和 KPWM(s)分别为电流环比例系数和变流器的放大倍数;Gd(s)为开关延时。

联立式(2)和式(3),得到等效阻抗为变流器的等效阻抗如图6所示。接入有源谐波电阻后,此时系统的模型阻抗曲线如图7。

图6 变流器等效阻抗Fig.6 Equivalent resistance of inverter

图7 接入有源谐波电阻后系统模态阻抗Fig.7 Modal impedance of the system with AHR
图6可以看出,在1 kHz以内,变流器输出特性近似等效于电阻特性,随着频率的增加,误差有所增大,表现为电阻和电感的串联特性。接入有源电阻后,模态阻抗λ-13在431 Hz处减小到原来的1%以内,谐振得到有效抑制。
3 电压控制电流源型有源谐波电阻特性研究
3.1 最优阻值及变流器容量评估
为了抑制关键谐振频率处谐波的放大,变流器和串联电感并联支路的阻抗应该在此频率处取得最大值,其并联阻抗表达式为

式中,ωn为关键谐振频率,根据上文分析,该系统关键谐振频率为431 Hz。当有源谐波电阻的等效阻值满足Reql=ωnL时,该频率处变流器和串联电感支路的阻抗|Zn|取得最大值。根据第1节给出的中压系统模型的算例,得出等效电阻约为11 Ω。
当等效谐波电阻的阻值确定后,进一步可以得到变流器的最大功率。在谐波频率上,电容和电感的阻抗比满足

式中:KL为基波电感率,即基频下串联电感和补偿电容电抗之比;h为谐波次数,h=5,7,…。节点②为补偿支路和非线性负载的PCC点,接入有源谐波电阻时,无功补偿支路串联电感电压为


根据式(8),串联电感承受的谐波电压小于PCC处的谐波电压,所以根据PCC处系统电压THD值可以计算出变流器端口所需要的谐波电压的最大值及变流器的最大谐波功率,即

在10 kV的配网系统中,要求THDu最大值为4%[17]。当等效电阻取11 Ω时,变流器单相的最大功率约为4.8 kW。
3.2 输出电流基波相位控制
无功补偿支路中含有大量的谐波,加上系统谐振时被放大的谐波,对变流器端口基波锁相有一定的困难。为了避开在强干扰环境下的锁相问题,利用交流母线上节点②处的PT装置做锁相,当仅含有LC无源支路时,节点③基波电压相位和节点②基波电压相位相差180°,其等效电路如图8所示。
图中,K为基波电流调节系数。当IF≠0时,变流器端口的实际基波电压相位和给定相位会发生改变。变流器端口实际的基波电压为

又因为变流器的基波有功能量用于平衡吸收的谐波有功能量,忽略变流器的损耗时,根据能量平衡关系,有


图8 基波频率下单相等效电路Fig.8 Single-phase equivalent circuit at fundamental frequency
根据变流器谐波功率的最大值,联立式(10)~式(12),可求解到K最大值约为0.01。
UPF和ULF分别是变流器母线基波电压和变流器端口基波电压,当K等于0时相位差180°,当K不等于0时其相位差和K值的关系如图9所示。

图9 交流母线和变流器交流侧基波电压相位差和K的关系Fig.9 Relationship between K and the phase difference of voltage at fundamental frequency between AC bus and AC-side inverter
当K为负值时,变流器输出基波有功能量;当K为正值时变流器吸收基波有功能量。较小的K值对锁相环节影响不大,通过交流母线基波电压近似得到变流器端口基波电压相位是有效的方式。
4 仿真及实验
引入本文提出的有源谐波电阻抑制谐振后,节点电压和支路电流仿真波形分别如图10和图11所示。由图可以看到,节点③上7次谐波电压成分明显地减小,其峰值减小到谐振前的1/5;其他特征频率的谐波成分均有一定的抑制。

图10 接入有源谐波电阻后节点电压波形Fig.10 Waveform of nodal voltage with AHR

图11 接入有源谐波电阻后支路电流波形Fig.11 Waveform of branch current with AHR
负载电流、无功补偿支路电流和电网电流波形如图11所示。由图可以看到,各支路中7次谐波电流放大现象有明显的抑制,无功补偿电容的电流峰值降为谐振抑制前的1/2,电容电流中的尖刺是由于不控整流器的换相导致,谐波成分含量很小。注入式有源谐波电阻也具有很好的动态特性,负载突变时的仿真结果如图12所示。在2.00 s时,负载突然增加,但是无功补偿直流电流基本保持不变,没有出现振荡问题。
实验验证基于实验室380 VAC的系统。非线性负载用二极管不控整流负载带48 Ω电阻模拟,无功补偿电容串联电感3.5 mH,其余实验参数同仿真。等效电阻取值约为9.5 Ω,实验波形分别如图13~图15所示。

图12 有源谐波电阻动态性能仿真结果Fig.12 Simulation results of the dynamic performance of AHR

图13 接入有源谐波电阻前无功支路电流和节点③电压实验波形Fig.13 Experimental waveforms of reactive branch current and voltage at node 3 without AHR

图14 接入有源谐波电阻后无功支路电流和节点③电压实验波形Fig.14 Experimental waveforms of active branch current and voltage at node 3 with out AHR

图15 变流器端口电压电流、波形Fig.15 Experimental result of voltage and current at the terminal of inverter
由图13、图14可以看到,引入有源谐波电阻后,谐振得到了抑制,此时变流器端口的电压和电流波形如图15所示。
接入有源谐波电阻阻尼前后实验结果的FFT数据对比如图16所示。根据图16可以看到,加入有源虚拟电阻后,电感电压和电容电流中的各次谐波成分均得到了有效的抑制。阻尼前和阻尼后电感电压的TDH分别为104%和42%;阻尼前和阻尼后电容电流的THD分别为25%和13%。并且,对系统关键谐振频率处的谐波抑制效果最明显,阻尼后电感电压和电容电流的7次谐波成分仅为阻尼前的22%和50%。

图16 实验波形的FFT结果Fig.16 FFT result of experimental waveforms
5 结语
模态谐振分析法在分析电力系统多端复杂网络中的谐振问题上具有很高的准确性,且计算简单。利用模态谐振分析法,除了能够得到谐振频率及各节点受到谐振电压影响的信息外,还可以判断出支路上受到谐振电流的影响情况。
利用电力电子变流器可以在比较宽的频带上模拟电阻的特性,用于阻尼系统的谐振具有很好的效果。利用注入式的结构,可以减小变流器交流侧承受的基波电压和电流,使其在中压配网电能质量治理中具有广阔应用空间。
参考文献:
[1]张海鹏,林舜江,刘明波,等.低压配电网无功补偿及效益评估系统的开发和应用[J].电力系统保护与控制,2016,44(4):129-136.Zhang Haipeng,Lin Shunjiang,Liu Mingbo,et al.Development of low voltage distribution networks reactive power compensation and benefit assessment system and its application[J].Power System Protection and Control,2016,44(4):129-136(in Chinese).
[2]谭树龙,杨耕,耿华.不平衡工况下链式STATCOM的运行极限分析[J].电力自动化设备,2015,35(1):44-49,78.Tan Shulong,Yang geng,Geng Hua.Analysis of operating limit for cascaded STATCOM in unbalanced condition[J].Electric Power Automation Equipment,2015,35 (1):44-49,78(in Chinese).
[3]刘艳阳.配电网无功补偿配置原则优化研究[J].陕西电力,2015,43(9):57-61.Liu Yanyang.Research on reactive compensation principle of configuration optimization in distribution grid[J].Shaanxi Electric Power,2015,43(9):57-61(in Chinese).
[4]唐振东,杨洪耕.基于模态分析的风电场并网谐波谐振研究[J].电力自动化设备,2017,37(3):87-92,99.Tang Zhendong,Yang Honggeng.Harmonic resonance research based on modal analysis for grid-connected wind farms[J].Electric Power Automation Equipment,2017,37(3):87-92,99(in Chinese).
[5]刘洋,帅智康,李杨,等.多逆变器并网系统谐波谐振模态分析[J].中国电机工程学报,2017,37(14):4156-4164,4295.Liu Yang,Shuai Zhikang,Li Yang,et al.Harmonic resonance modal analysis of multi-inverter grid-connected systems[J].Proceedings of the CSEE,2017,37(14):4156-4164,4295(in Chinese).
[6]Xu W,Huang Zhengyu,Cui Yu,et al.Harmonic resonance mode analysis[J].IEEE Transactions on Power Delivery,2005,20(2):1182-1190.
[7]彭莉萍,魏辉,刘桂平,等.通过改进Prony算法辨识交流串补引起的次同步谐振模态参数[J].电力系统及其自动化学报,2015,27(S1):63-67.Peng Liping,Wei Hui,Liu Guiping,et al.Detection of subsynchronous resonance caused by series capacitive compensation based on improved Prony[J].Proceedings of the CSU-EPSA,2015,27(S1):63-67(in Chinese).
[8]余光正,林涛,陈汝斯,等.考虑智能配电网谐波谐振模式不确定性的抑制措施[J].电力自动化设备,2016,36(7):60-66.Yu Guangzheng,Lin Tao,Chen Rusi,et al.Harmonic reso-nance suppression considering harmonic resonance mode uncertainty of smart distribution grid[J].Electric Power Automation Equipment,2016,36(7):60-66(in Chinese).
[9]张笠君,汪飞,郭慧,等.微电网谐振建模与抑制方法的研究现状[J].电源学报,2016,14(2):52-62.Zhang Lijun,Wang Fei,Guo Hui,et al.Research status of resonance modeling and suppressionin in microgrid[J].Journal of Power Supply,2016,14(2):52-62(in Chinese).
[10]He jinwei,Li Yunwei,Munir S.A flexible harmonic control approach through voltage controlled DG-Grid interfacing converters[J].IEEE Transactions on Industrial Electronics,2012,59(1):444-455.
[11]He Jinwei,Li Yunwei,Blaabjerg F.Active harmonic filtering using current-controlled,grid-connected DG units with closed-loop power control[J].IEEE Transactions on Power Electronics,2013,29(2):642-653.
[12]王小伟,赵伟,涂春鸣,等.双谐振注入式混合有源电力滤波器及控制方法[J].电力系统自动化,2010,34(2):59-63.Wang Xiaowei,Zhao Wei,Tu Chunming,et al.Novel active power filter with double-resonance injection circuit and its control strategy[J].Automation of Electric Power Systems,2010,34(02):59-63.(in Chinese).
[13]汤赐,姚舜,帅智康,等.新型注入式混合有源滤波器的稳定性研究[J].电网技术,2006,30(20):56-60.Tang Ci,Yao Shun,Shuai Zhikang,et al.Research on stability of new injection type hybrid active power filter[J].Power System Technology,2006,30(20):56-60(in Chinese).
[14]Luo An,Shuai Zhikang,Zhu Jiwen,et al.Combined system for harmonic suppression and reactive power compensation[J].IEEE Transactions on Industrial Electronics,2009,56(2):418-428.
[15]Zhang Xiang,Lei Wanjun,Sheng Ruyang,et al.Research on protection of power capacitor using active harmonic resistance[C].Applied Power Electronics Conference and Exposition(APEC),2012 Twenty-Seventh Annual IEEE.2012:2229-2233.
[16]Bellman R.Introduction to Matrix Analysis[M].2nd ed.New York:McGraw-Hill,1970.
[17]中国国家标准GB/T 14549-93:电能质量 公用电网谐波[S].北京:中国标准出版社,1994.China National Standard GB/T 14549-93:Power grid harmonic[S].Beijing:China Standard Press,1994(in Chinese).

