基于稀疏编码局部时空描述子的动作识别方法

赵晓丽，田丽华，李　晨

ZHAO Xiaoli,TIAN Lihua,LI Chen

西安交通大学 软件学院，西安 710049

School of Software Engineering,Xi’an Jiaotong University,Xi’an 710049,China

1　引言

人体动作行为识别是近年来计算机视觉领域的一个研究热点，其广泛应用于人机智能交互、虚拟现实和视频监控等领域[1]。在以往的研究中，往往通过从可穿戴传感器或视频中采集的动作图来进行人体动作识别，过程过于繁琐，且受环境和噪音影响较大。但随着低成本、易操作的Kinect设备的出现，基于深度数据的动作识别受到了研究人员的欢迎。利用Kinect设备采集的人体动作信息不仅对环境中的颜色、光照和纹理不敏感，而且可以实时获取人体深度图像。利用文献[2]中的方法可以快速准确的从深度图像中评估人体骨骼关节点的空间位置，相对于传统的视频具有视角无关系。基于深度图像的行为识别对噪声和遮挡更具有鲁棒性[3]，动作识别主要可分为数据采集与预处理、特征提取、特征处理、分类识别等几个步骤，其中特征提取和处理最为重要。Yang等[3]通过聚集深度序列中的曲面法线构建特征向量，然后在时空网格上分别进行稀疏编码和池化来构建可区分性强的特征描述子（SNV）。文献[4]提出了HON4D描述子，首先用投影向量量化4D空间，然后将动作序列分割成时空方块，分块统计法线方向分布直方图作为最终特征向量。文献[5]通过提取点云数据中的主成分向量，然后投影到以正二十面体的顶点向量所确定的方向上，来构建方向主成分直方图（HOPC），对速度和角度的变化具有很好的鲁棒性。

分类识别目前有基于模板匹配、基于统计、基于语义的方法，以及一些其他分类方法。基于模板匹配的方法主要有动态时间规整法[6]、动态规划法[7]和模板匹配法等。动态时间规整和动态规划法可以消除动作运动速度不一致对识别的影响；模板匹配法适合于简单的动作识别，由于个体对动作理解的差异，很难对动作定义一个标准的模板。基于统计的方法主要有隐马尔科夫模型（HMM）[8]和动态贝叶斯模型（DBN）[9]，识别效果较好，但往往有很多特征参数需要选取，参数选取的好坏直接影响识别结果。基于语义识别的方法更目前仅能对简单语义进行识别，无法应用于复杂场景。除此之外，近年来支持向量机（SVM）[10]、卷积神经网络（CNN）[11]在动作分类中应用广泛。

支持向量机（SVM）分类可拓展到多分类，是目前最普遍使用的分类方法。Chang等[12]提出的LIBSVM分类工具可简单有效的进行模式识别与回归，但训练速度较慢。Fan等[13]提出的LIBLINEAR分类器主要为大规模数据而设计的线性模型，采用线性核，计算速度更快。由于粒子群算法原理简单且易于求值，逐渐被用来优化SVM分类器。文献[14]提出的基于检测策略的骨干粒子群算法，适应度函数使用弹性网络估计方法，能使算法更加稳定且加速收敛。文献[15]提出的借鉴复杂适应度系统（CAS）理论，将混沌和自适应引入到基本PSO中，形成一种双重自适应PSO算法，解决算法易陷入局部最优等问题。

通过对文献[3-4]所提出的方法进行分析，针对其特征冗余、训练速度慢，以及识别率不高等问题提出了基于稀疏编码局部时空描述子的动作识别方法。首先对Kinect设备采集的深度图像进行法线提取，同时利用基于能量的自适应时空金字塔对动作序列进行时空分块。然后局部时空法线，减少冗余信息，得到显著特征向量，即局部时空描述子。随后将法线特征进行稀疏编码[16]得到一组字典向量来重构样本数据。对于每一块时空的特征向量应用已求得的字典来稀疏编码和池化，降低特征维度；最后利用sPSO优化的SVM分类器，可以得到更符合样本数据的模型。

2　理论基础

2.1　法线

法线是始终垂直于某平面的虚线，用来描述几何体表面的方向。图像法线特征能够捕获丰富的信息，具有很好的辨别性，能更好地完成动作识别任务。

在深度序列中，3D空间可以拓展成一个混合4D空间。R3→R1:z=f(x,y,t)，其中(x,y,t)是第t帧点云的空间坐标。每个点云(x,y,t)满足S(x,y,t,z)=f(x,y,t)-z=0；4D空间表面S的法线特征可以由公式（1）求得，每个像素点应有一条法线，如图1为法线示意图。

图1　法线示意图

4D法线相对于传统梯度方向更有能力获取丰富且可区分性强的信息[4]。

2.2　时空金字塔

考虑到每帧特征之间具有一定的时空关系，因此通过时空金字塔进行特征聚集。时空金字塔不仅能够捕获动作序列的空间结构也能获得动作序列的时间信息。

为获取空间维度上的信息，将每一帧分为nH×nW块；为获取时间维度的信息，将整个动作分为T级；最终每个动作序列将分成nH×nW×(2T-1)块。本文在时间维度上使用3级金字塔：{t0t4},{t0t2,t2t4},{t0t1,t2t3,t3t4}，因此时空金字塔共划分成了nH×nW×7块。图2为3级时空金字塔在时间维度上的示意图。

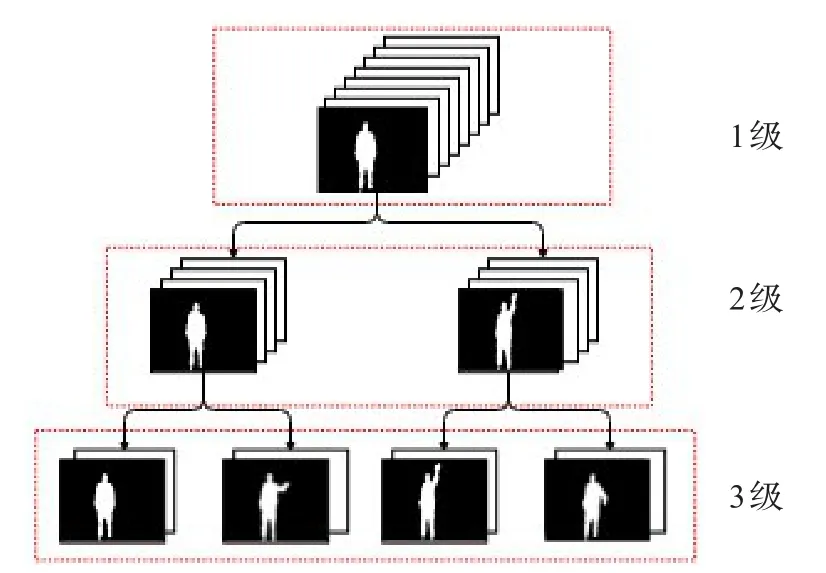
图2　时空金字塔示意图（3级共分为7块）

时空金字塔的第1级表示动作的整体特征，第2级和第3级分别代表了动作不同部分的局部特征。时空金字塔加入了动作的空间结构，可以显著提升不同类型动作之间的区分度，从而提升分类的准确性和鲁棒性。

2.3　稀疏编码

稀疏编码是一种无监督学习方法，用来寻找一组字典向量来重构样本数据。白化后的样本数据P=(p1,p2,…,pN)∈RM×N，其中 Pi代表每帧动作的特征值。用公式（2）来获得字典D和相关系数：

其中，字典 D∈RM×K，是字典D中的虚拟单词；αi∈RM×N是稀疏分解系数；λ是正则系数。

2.4　简化粒子群算法

由Elberhart和Kennedy最早提出的粒子群优化算法（bPSO）[17]，系统初始化为一组随机解，通过迭代搜寻最优值[18]，算法公式如下：

为了提高粒子群跳出局部极值的能力，Shi等[19]对公式（3）添加了惯性因子ω：

文献[20]证明了粒子群的进化与速度无关。假设种群中除第i个粒子外其余粒子保持不动，可以省略下标i；假设粒子群的维数为一维，则可以省略下标d，再为便于理解，将式中的变量符号移到变量符后的括号中，则式（4）和（5）可以变为：

式（8）是不含速度项的经典二阶微分方程（假设粒子的位置移动为连续过程）[20]。综上所述，不含速度项的粒子群公式为：

sPSO算法可以没有粒子速度的概念，避免了设定参数[-vmax,vmax]而影响粒子的收敛速度和收敛精度[18]，适用于算法优化、参数寻优等情况。

本文利用sPSO来寻求SVM中惩罚系数C的最优值。简化粒子群算法sPSO的实现步骤为：

（1）初始化粒子群相关参数。种群大小为M，每个粒子初始位置x，惯性因子ω，加速常数c1、c2，局部最优 pid和全局最优 pgd。

（2）计算每个粒子的适应度值。

（3）每个粒子的适应度值分别与个体最优 pid比较，取最优的一个。

（4）用每个粒子的适应度值分别与全局最优 pgd比较，取最优的一个。

（5）根据公式（9）更新粒子的位置。

（6）满足结束条件（达到最大迭代次数N或在误差范围内），则退出；否则返回（2）。

3　基于局部时空描述子的人体动作识别算法

本文在法线的基础上，局部聚集法线得到时空局部描述子。为提取时间和空间上动作序列的相关信息，使用基于能量的自适应时空金字塔对动作进行分块。为了减少冗余的法线信息，对提取到的特征先稀疏编码后池化。最终送入sPSO优化的SVM分类器进行分类。总体的算法流程图3所示。

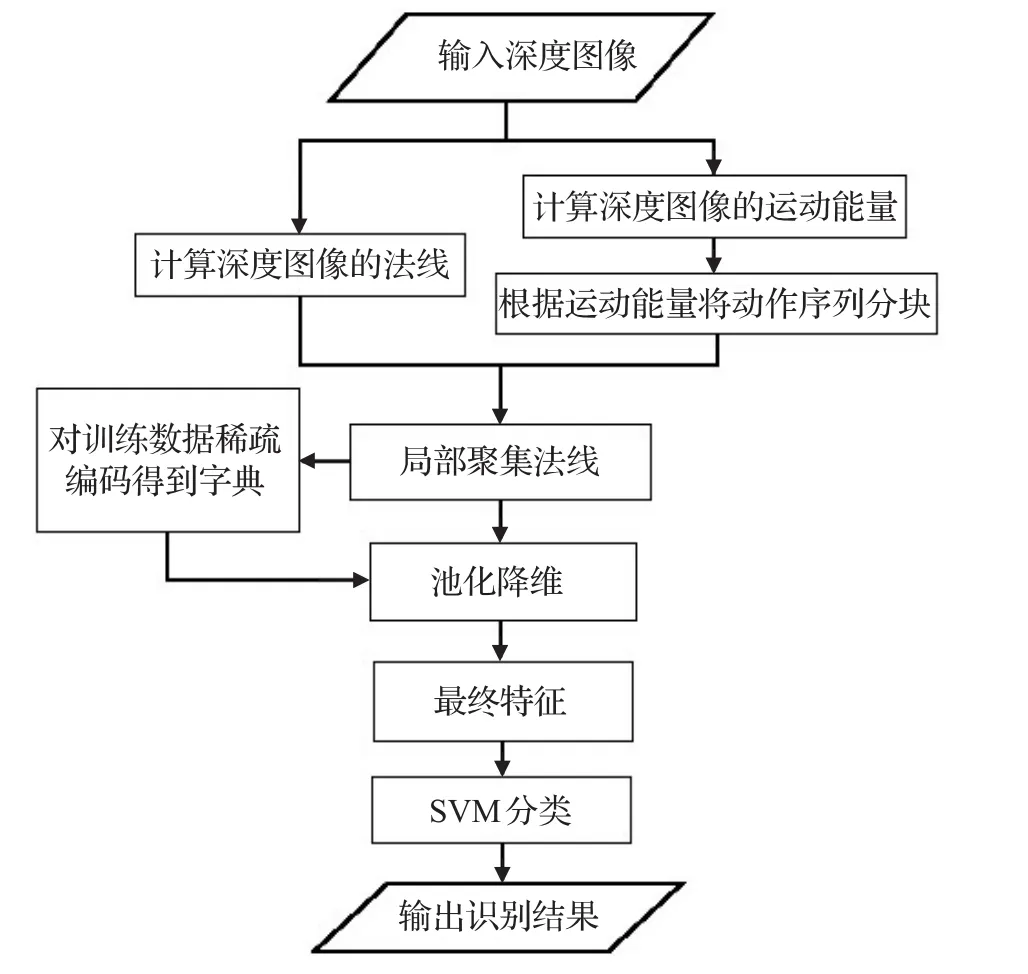
图3　算法流程图

3.1　局部时空描述子

文献[3]中使用基于时空的描述子，将点云lr×lc×lt邻域串联起来组成lr×lc×lt×3维邻域法线，但却包含大量重复信息。文献[4]提取的HON4D描述子在时空中统计法线方向直方图，虽然提取出了一定的显著特征，但却部分丢失了曲面方向的信息。

为了减少邻域法线重复信息又不至于丢失显著性特征，提高算法的鲁棒性，若先将每个动作序列分成nH×nW×(2T-1)块，再将每块均分为若干块求每块法线均值后串联起来作为最终特征，虽有效降低了特征维度，但无法足够准确地表达运动特征。若将每个点云邻域lr×lc×lt中的法线平均起来表征中心点云，虽去除了部分噪声对动作序列的影响，但仍无法提取出显著性特征。

因人体动作是在时间轴上连续运动的空间序列，故考虑聚集行、列、帧平面的法线表达运动特征，行、列为提取空间维度上的运动特征，帧即为时间维度上的运动表征，最终应用局部时空描述子来进行特征提取。

对于每个点云，在邻域lr×lc×lt中分别聚集过中心点的行、列、帧平面的法线，得到9维法线特征。在4D表面中，只有法线的方向是与图像表面形状息息相关的。对于lr×lc×lt组成的局部邻域R，行聚集法线由公式（10）可得：

公式中的[]表示向上取整。混合局部邻域法线P由行、列、帧平均法线串联而来，即

nly、nlt的特征同nlx。所有点云平均法线的串联即每一帧的特征描述子P，即

图4为3×3×3局部时空描述子示意图，分别聚集蓝、紫、黄3个平面内的法线后串联起来，即为块中心点的局部时空描述子。

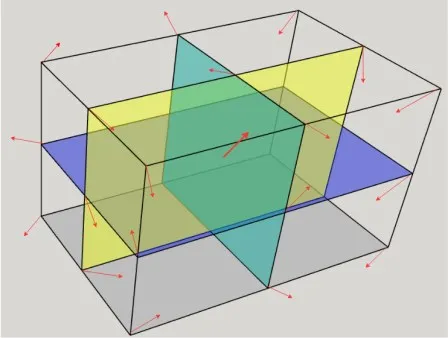
图4　局部时空描述子提取示意图

3.2　基于运动能量的自适应时空金字塔

在对动作进行分类前，为了提高分类的准确性和鲁棒性，本文提出自适应时空金字塔即将动作序列在时间和空间维度上分块，对块内法线进行进一步的处理，以达到更好的识别结果。

在空间维度上，首先对每帧姿态提取出包含人体动作的最小区域，消除无动作背景的影响，然后将每帧动作分为nH×nW块。在时间维度上划分金字塔时，由于不同的动作被记录的速度和运动速度都会直接导致动作帧序列的不同，若时间轴上直接平均分块会导致一定的差异。为了消除这些差异，用累加的运动能量来构建能量曲线，能量曲线在一定程度上反映了人体动作姿态的变化以及速度的快慢。

为了获取运动能量，本文用了一个简单有效的方法来移除静态帧。假设Fi-1和Fi是相邻的两帧，则运动能量的公式由公式（13）获取：

其中，ε表示去除噪音的阈值；sum()·返回帧差值的非零元素总数；第i帧的运动能量即为第1帧到第i帧的能量叠加。

获取到的运动能量一般为105级别的数值，用式（14）归一化到[0，1]区间，归一化后最接近1/n的即为n分的帧节点。

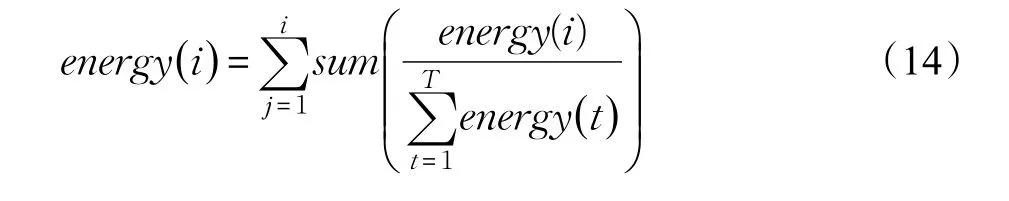
其中，T为动作序列的长度减1。如图5为使用能量分块与普通分块对比图。

图5　使用能量分块与普通分块对比

图5上图为直接均分示意图，分块区间为[1，11，23，34，45]；下图为使用运动能量分块示意图，分块区间为[1，27 34，39，45]。由图可以看出，前10帧几乎处于静止状态，而35～40帧运动变化较大，使用运动能量能够根据动作变化情况更加均匀的分块，不受运动速度或记录速度等的影响。

3.3　降维

池化操作不仅能提取出特征中可区分性强的特征，同时也可降低图像特征的维数。池化操作分为平均池化和最大化池化两种。对于每一个时空网格，在空间上应用平均池化：

其中，uk(t)代表第k个虚拟单词在第t帧的差分向量。

在时间上应用最大化池化：

其中，uk,i代表第k个虚拟单词向量中相对应第i个值。向量就是一个时空网格的特征。最后，将时空网格的特征向量串联起来即为最终特征向量。

3.4　sPSO优化SVM分类

SVM中惩罚系数C代表的是在线性不可分的情况下，对分类错误的惩罚程度，C值过大容易造成过拟合，C值过小容易造成欠拟合。为了获得SVM中的最优惩罚系数C，利用简化粒子群算法（sPSO）进行迭代求取。传统PSO算法易陷入局部极值且收敛速度慢，sPSO算法消除了粒子速度的影响，避免了速度参数对粒子的收敛速度和收敛精度的影响。在利用sPSO求解最优惩罚系数C时，初始设置c1=1.5，c2=1.7，种群规模M=20，惯性因子w=1，由于训练样本数量庞大，为了减少时间成本，设置最大迭代次数为N=200或误差范围在10－3内。因训练数据维数较高，故求解过程中的模型训练使用LIBLINEAR工具箱。使用粒子群优化惩罚系数增加的时间复杂度为O(MN)，由表2和表6可看出，虽然求取最优惩罚系数的过程虽然提升了运算量，但却提升了大于1%的识别率。经过实验对分分析求得，对于MSRAction3D和MSRGesture3D数据集的最优惩罚系数为0.3～0.7。

4　实验结果及分析

4.1　数据集

为了验证本文提出的基于稀疏编码局部时空描述子的识别算法的鲁棒性，分别在公共数据集MSRAction3D和MSRGesture3D上进行了测试。两个深度序列数据集部分动作如图6和图7所示。

图6　MSRAction3D中high arm wave深度图像

图7　MSRGesture3D中画Z深度图像

MSRAction3D数据集[21]是用Kinect设备获取到的动作帧的深度序列，包含20个动作：“high arm wave”“horizontal arm wave”“hammer”“hand catch”“forward punch”“high throw”“draw x”“draw tick”“draw circle”“hand clap”“two hand wave”“side boxing”“bend”“forwardkick”“sidekick”“jogging”“tennisswing”“tennis serve”“golf swing”“pick up&throw”，每个动作分别由10个人做2～3次。该数据集的识别难度在于其中的很多动作很相似。

MSRGesture3D数据集[22]是由Kinect设备获取手势的深度图像，它包含了被ASL定义的12个手语动作：“bathroom”“blue”“finish”“green”“hungry”“milk”“past”“pig”“store”“where”“j”“z”，每个动作分别由 10 个人做2～3次。该数据集的挑战主要是自遮挡的问题。

4.2　实验结果及分析

在MSRAction3D数据集上，第1、3、5、7、9个人的动作作为训练数据，第2、4、6、8、10个人的动作作为测试数据，混淆矩阵如图8所示。在两个数据集的实验中式（2）的正则系数λ取0.15，式（13）的能量阈值ε取100。

从图8可以看出，20个动作里有15个动作的识别率可达100%，而误识别则出现在了比较相似的动作上，例如high throw和hand catch。

如图9为在MSRAction3D数据集上字典数量与识别率的关系。图9上图为字典数量在10～100以10为梯度的字典数量与识别率的关系；下图则为100～400以100为梯度的字典数量与识别率的关系。由图可以看出，当字典数量设为100的时候识别精度最高。

表1为字典大小设置为100时MSRAction3D数据集中时空网格大小和识别率的关系，可以看出时空网格并设置为5×5×5最为合适。

表1　MSRAction3D中时空网格大小和识别率的关系

表2为仅使用sPSO优化、仅使用能量分块优化和sPSO+能量分块优化后与优化前的识别率对比。可以看出，单独使用sPSO算法寻求最优惩罚系数后，算法精度提高了1.09%。单独使用运动能量分块能够更加精准地分割动作序列，算法精度提高了1.46%。sPSO和能量分块优化后，算法精度提高了2.19%

表2　MSRAction3D中优化前后对比

将本文提出的识别方法与其他人体行为识别方法相对比，平均识别率的对比如表3所示。

表3　在MSRAction3D上的识别率比较结果

在MSRGesture3D数据集上，第1、3、5、7、9个人的动作作为训练数据，第2、4、6、8、10个人的动作作为测试数据，混淆矩阵如图10所示。

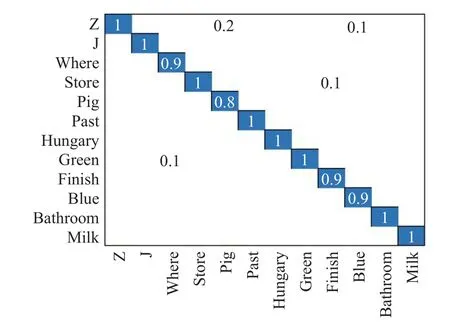
图10　MSRGesture3D混淆矩阵

从图10可以看出，在12个动作中有8个动作的识别率达到了100%，同样的，Z和Pig动作在手语中十分相似，出现了误识别的情况。

如图11为MSRGesture3D数据集字典数量与识别率的关系，由图可以看出，当字典数量设为20的时候识别精度最高。

表4为字典大小设置为20时，MSRGesture3D数据集中时空网格大小和识别率的关系，可以看出时空网格并设置为3×3×3最为合适。

图11　MSRGesture3D字典数量与识别率

表4　MSRGesture3D中时空网格大小和识别率的关系

将本文提出的识别方法与其他手势动作识别方法，平均识别率的对比如表5所示。

表5　MSRGesture3D上的识别率比较结果

实验所用平台为Intel®E5-2609处理器，CPU@2.5 GHz，128 GB内存的Win7 64位操作系统，开发工具为MATLAB R 2017b。平均每帧运行时间，如表6所示。

表6　平均每帧运行时间s

本文提出的方法从特征维度上相对于SNV降了9倍，在MSRAction3D数据集上平均每帧的处理速度约提高了5倍，而在MSRGesture3D数据集上约提速了2倍。

5　结束语

为解决已有算法特征维数过高导致训练速度较慢以及识别率不高等问题，本文提出基于稀疏编码局部时空描述子的动作识别方法，在时空维度上聚集提取到的法线，利用稀疏编码求取字典来重构数据。为了能提取更加显著的特征，提出基于运动能量的自适应时空金字塔，对动作分块；然后对分块后的动作分别池化降维，得到最终特征送入sPSO优化后的SVM分类器分类。通过在MSRAction3D和MSRGesture3D数据集上实验，结果验证了本文提出的识别方法具有很好的识别率和鲁棒性。

参考文献：

[1]李瑞峰，王亮亮，王珂.人体动作行为识别研究综述[J].模式识别与人工智能，2014，27（1）：35-48.

[2]Shotton J，Kipman A，Kipman A，et al.Real-time human pose recognition in parts from single depth images[J].Communications of the ACM，2013，56（1）：116-124.

[3]Yang X，Tian Y L.Super normal vector for activity recognition using depth sequences[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition，2014：804-811.

[4]Oreifej O，Liu Z.HON4D：Histogram of oriented 4D normals for activity recognition from depth sequences[J].Computer Vision and Pattern Recognition，2013，9（4）：716-723.

[5]Rahmani H，Mahmood A，Du Q H，et al.HOPC：Histogram of oriented principal components of 3D pointclouds for action recognition[C]//Proceedings of European Conference on Computer Vision，2014：742-757.

[6]李正欣，张凤鸣，李克武，等.一种支持DTW距离的多元时间序列索引结构[J].软件学报，2014，25（3）：560-575.

[7]Bobick A F，Wilson A D.Using configuration states for the representation and recognition and gesture[R].Cambridge，Massachusetts：MIT Media Lab Perceptual Comuting Section Technical Report，1995.

[8]Ji X，Liu H，Li Y.Human actions recognition using fuzzy PCAanddiscriminativehiddenmodel[C]//Proceedings of IEEE International Conference on Fuzzy Systems，2010：1-6.

[9]Murphy K P.Dynamic bayesian networks[C]//Proceedings of Probabilistic Graphical Models.2002：27-56.

[10]Bartlett M S，Littlewort G，Frank M，et al.Recognizing facial expression：Machine learning and application to spontaneous behavior[C]//Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition，2005：568-573.

[11]张顺，龚怡宏，王进军.深度卷积神经网络的发展及其在计算机视觉领域的应用[J].计算机学报，2017（S）：1-29.

[12]Chang Chihchung，Lin Chihjen.LIBSVM：A library for support vector machines[J].ACM Transactions on Intelligent Systems and Technology，2011，2（3）：1-27.

[13]Fan R E，Chang K W，Hsieh C J，et al.LIBLINEAR：A library for large linear classification[J].Journal of Machine Learning Research，2008，9：1871-1874.

[14]李光早，王士同.基于骨干粒子群的弹性稀疏人脸识别[J].计算机工程与应用，2017，53（17）：143-148.

[15]刘举胜，何建佳，李鹏飞.基于CAS理论的改进PSO算法[J].计算机工程与应用，2017，53（5）：57-63.

[16]Yu C N，Mirowski P，Ho T K.A sparse coding approach to household electricity demand forecasting in smart grids[J].IEEE Transactions on Smart Grid，2017，8（2）：738-748.

[17]Kennedy J，Eberhart R.Particle swarm optimization[C]//Proceedings of IEEE International Conference on Neural Networks，2002：1942-1948.

[18]任江涛，赵少东，许盛灿，等.基于二进制PSO算法的特征选择及SVM参数同步优化[J].计算机科学，2007，34（6）：179-182.

[19]Shi Y，Eberhart R.A modified particle swarm optimizer[M]//Advances in Natural Computation.Berlin Heidelberg：Springer，1998.

[20]胡旺，李志蜀.一种更简化而高效的粒子群优化算法[J].软件学报，2007，18（4）：861-868.

[21]Li W，Zhang Z，Liu Z.Action recognition based on a bag of 3D points[C]//Proceedings of Computer Vision and Pattern Recognition Workshops，2010：9-14.

[22]Wang J，Liu Z，Chorowski J，et al.Robust 3D action recognition with random occupancy patterns[C]//Proceedings of European Conference on Computer Vision，2012：872-885.

[23]Xia L，Chen C C，Aggarwal J K.View invariant human action recognition using histograms of 3D joints[C]//Proceedings of European Conference on Computer Vision，2012：20-27.