结合K近邻的改进密度峰值聚类算法

薛小娜，高淑萍，彭弘铭，吴会会

XUE Xiaona1,GAO Shuping1,PENG Hongming2,WU Huihui1

1.西安电子科技大学 数学与统计学院，西安 710126

2.西安电子科技大学 通信工程学院，西安 710071

1.School of Mathematics and Statistics,Xidian University,Xi’an 710126,China

2.School of Telecommunications Engineering,Xidian University,Xi’an 710071,China

1　引言

聚类是数据挖掘领域中的一种无监督分类方法，其目的是将混乱的数据进行分组，使得同一簇中的样本尽可能相似，而不同簇中的样本尽量不同[1-3]，现已被广泛应用于信息检索、模式分类及数据挖掘等领域[4]。基于不同学习策略，传统聚类算法可被划分为分割聚类（如K-means[5]）、密度聚类（如DBSCAN[6]），以及基于传播的方法（如AP[7]）等。

文献[8]提出了一种新颖的密度峰值聚类算法DPC，其不仅能检测出样本集中存在的聚类数目，而且能够有效处理具有不规则形状的簇以及异常样本。尽管DPC算法优势明显，但其仍存在一些局限：（1）对于大小不同的数据集，采用的局部密度计算方式不同，这无形中降低了算法的灵活性；（2）对剩余点的分配策略易造成误差传播。近两年来，许多学者都在对DPC算法进行改进，虽取得了许多研究成果，但也发现了一些新问题。例如，文献[9]基于信息熵理论提出了一种从原始数据集中自动获取截断距离参数的新方法，但其所需的时间成本大大增加；文献[10]将DPC算法和Chameleon算法的优点相结合提出了E_CFSFDP算法，虽避免了将包含多个密度峰值的一个类聚成多类，但其计算开销高达O(N2+NlbN+NM)且不利于处理高维数据。由于 K 近邻（K-Nearest-Neighbors，KNN）具有简单、高效等特点，它不但可以处理文本分类以及流数据分类问题，其在聚类中也展现出很强的技巧性[11-13]，故该方法不断被引入DPC算法。例如，文献[14]提出了DPC-KNN算法，其利用KNN思想来估计每点的密度，并使用主成分分析方法对数据降维，提高了对高维数据的处理能力且能获得良好的聚类效果。然而，由于DPC-KNN算法的聚类过程与DPC相同，故DPC算法的缺陷在该算法中仍存在。文献[15]将模糊加权KNN引入DPC算法提出了FKNN-DPC算法，也使用KNN来计算每点的密度，并利用新提出的分配策略对剩余点进行分配，虽提高了聚类质量，但其模型较为复杂[16]。

针对上述问题，本文根据各样本的相似程度给出一种可适用于任意数据集的局部密度计算方法，以增强算法灵活度；受KNN以及队列思想的启发，设计了两种不同的策略来分配剩余点，以提升聚类质量和聚类效率。在21个常用数据集上的实验结果表明，本文算法IDPCA不仅减少了运行时间，而且提升了聚类质量。

2　DPC算法

DPC算法基于以下两点假设进行设计：（1）聚类中心点总是被低密度点包围；（2）聚类中心与其他高密度点间的距离相对较远。将待聚类数据集记为X，其大小和维度分别为N和D。对于X中的任意数据点xi，其分布情况由两个属性刻画，即局部密度ρi及该点与其他具有较高密度点之间的最小距离δi。ρi的计算方式为：

其中，φ(x)是分段函数，当 dij＜dc时，φ(x)=1；否则φ(x)=0；dc为截断距离参数；dij为点 xi和xj间的距离；ρi可解释为点xi的dc邻域内点的个数。对于较小的数据集，由式（1）估计的密度可能会受统计误差的影响，此时采用式（2）来估计其局部密度[8]。

xi的距离δi定义为：

对于局部密度最大的点xi，其距离为δi=majx (dij)。

DPC算法通过引入一种启发式方法（决策图）来帮助用户获取聚类中心（或称密度峰值）。图1（a）显示了由4个类组成的数据分布情况。为了获取该数据的聚类中心，DPC算法首先将每点的ρ值和δ值于坐标平面内绘出，然后将ρ和δ值都较大的点作为聚类中心，即图1（b）中右上角的4个数据点。然而，对于分布稀疏的数据，通过ρ-δ决策图难以确定其聚类中心，此时DPC算法使用γ=ρ×δ来获取，其中γi值越大，xi越可能是聚类中心。将所有点的γ值降序排列，并于坐标平面上绘出，如图1（c）所示。由于聚类中心的γ值较大，而其他点的γ值较小且呈平滑趋势，故可使用一条平行于横轴的直线将其分开，使得直线上方的γ值所对应的点即为聚类中心。当聚类中心找出后，将剩余点分配到其高密度最近邻所属的类中。

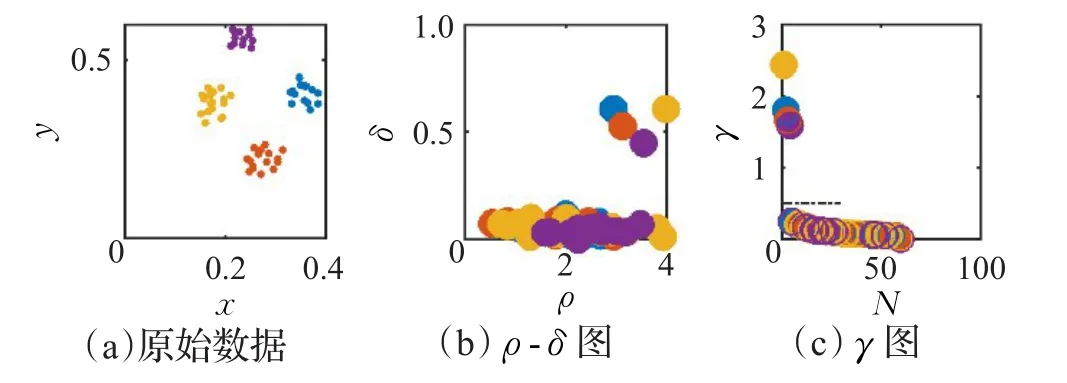
图1　DPC算法

3　IDPCA算法

3.1　算法思想

对于密度聚类算法来说，各样本密度的估计准确与否不仅影响聚类中心的选取，其对聚类质量也有直接影响。

由距离δ定义可知，δ值的大小与密度ρ也密切相关，故ρ对于聚类中心的选取至关重要。由于DPC算法的密度计算方法不一致且深受截断距离dc影响，其不能够保证与当前点距离小于dc的点的数目[15]，故有不少成果对该算法中的密度公式进行了改进。例如，DPC-KNN[14]和FKNN-DPC[15]算法为了消除dc的影响，均从数据局部分布情况出发，利用KNN来估计密度，其计算方式分别为：

尽管改进方法中的参数K比dc容易确定，但面对类间样本数不均衡以及疏密度不一的数据，使用γ=ρ×δ方式选取聚类中心时，类中心点与其他点的区分度并不高。为了以较高区分度识别出任意数据集中的聚类中心，本文从数据的整体分布出发，通过引入相似性系数来调节各点对当前点的密度贡献权重，给出一种带有相似性系数的高斯核函数来计算其局部密度。

对于每个数据点xi，其局部密度ρi定义为：

其中，σ取数据量的2%[8]，r为相似性系数，表示密度函数与数据点间相似度的关系程度，该值越大，距离点xi越近的点对其密度ρi的贡献权重越大。聚类中心的择取方式类似于DPC算法，即先利用式（3）和式（6）计算各点的δ和ρ值，然后通过γ值决策图辅助获得M个局部类的聚类中心，即选取较大的前M个γ值对应的点。

因本文算法IDPCA、DPC、DPC-KNN及FKNN-DPC计算距离δ的方式相同，仅密度计算方法不同，故可通过γ=ρ×δ值来比较各密度公式。图2（a）显示了由3个类组成的合成数据集；图2（b）～（f）显示了采用不同密度方法得到的γ值决策图，各参数为K=4，dc=1，r=2。图2中，所采用的计算方式依次为式（2）、式（1）、式（4）～（6）。

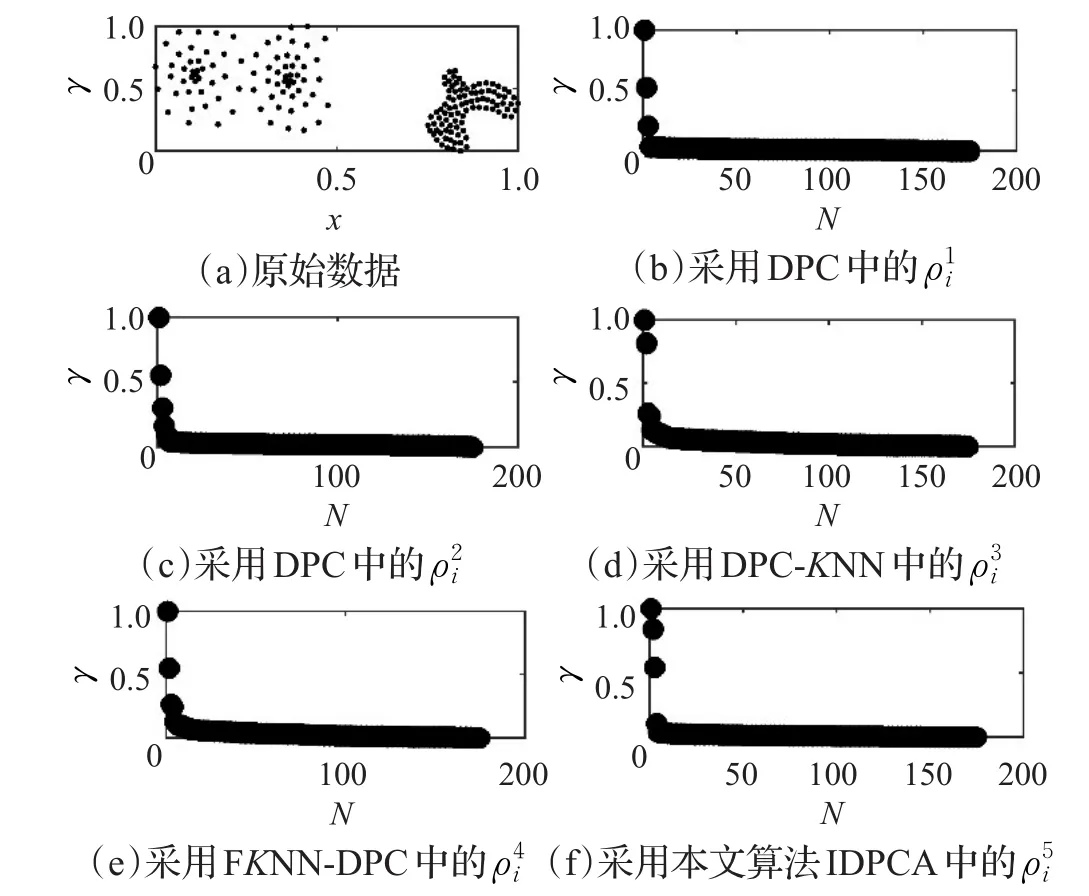
图2　采用5种不同密度方法计算的γ值

观察图2可以发现，与DPC算法相比，本文算法IDPCA能够以较高区分度识别出图2（a）数据中的3个聚类中心，而DPC-KNN算法和FKNN-DPC算法仅区分出两个，故本文提出的密度度量方式在聚类中心选取方面具有一定的优势。

由于聚类中心往往出现在高密度区域，故将各聚类中心某邻域内的点看作核心点，而将其他点看作非核心点。核心点的获取方法为：先将剩余点均分配到距其最近的聚类中心所在的类中，然后计算各局部类Cm中所有点与其类中心cenm间的平均距离um，若xi∈Cm在cenm的εum邻域内（即满足式（8）），则 xi为核心点。

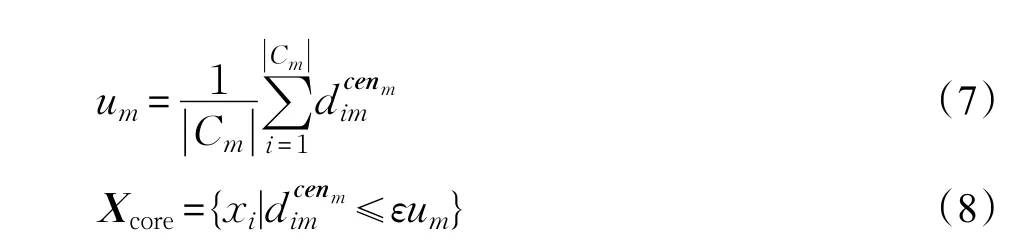
其中，|Cm|为第m个局部类Cm中的所有数据点的数目，(i=1,2,|Cm|,m=1,2,…,M)为点 xi∈Cm与cenm间的距离；分离阈值ε与数据集大小N有关，为N‰；Xcore为核心点集合。

为了将剩余点（非核心点）正确归类，本文设计了两种分配策略：全局搜索分配策略和统计学习分配策略。前者是以Xcore中的每点为中心，不断地搜索其未分配的KNN并将之分配到该点所在的局部类中。后者则是通过学习每个剩余点被分配至各局部类的概率来将其归类，其学习过程如下：首先依式（9）计算xi与xj的相似度sij，若两点距离越近，则其相似度越高。每点的归属由其KNN分布信息决定，若xi的KNN（KNNi）中属于Cm的点越多且与xi的距离越近，则sij值越大，此时xi被分配到Cm的概率Pmi也越大。Pmi的计算方式如式（10）所示。

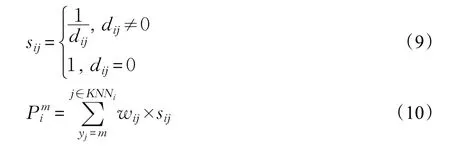
3.2　算法步骤

输入：数据集X，相似性系数r，最近邻个数K。

输出：类标签labels。

步骤1使用式（3）和（6）计算每点的δ与ρ值。

步骤2通过决策图获取聚类中心。

步骤3使用式（7）和（8）提取核心点，并采用全局搜索分配策略将待分类点归类：

（1）将核心点集合Xcore置入队列Q。

（2）取队列头xa，并将之从Q中删除，然后查找其K个最近邻KNNa。

（3）若 x′∈KNNa未被分配，则将 x′分配到 xa所在的类中，并将x′添加至Q尾部；否则转（2）。

步骤4采用统计学习策略分配剩余k个点：

（2）若MP中有非零值，则将Pmo值最大的点xo归入MI(o)所表示的类中，转（3）；否则终止该策略。

（3）更新P、MP、MI，令MP(o)=0。对于未分配点xp∈KNNo，更新 P[p][m]、MP(p)及 MI(p)。

（4）若MP中所有元素均为0，则终止；否则转（3）。

步骤5仍未被处理的点可看作噪声点，并将之归入到其最近邻所在的类中。

3.3　算法时间复杂度

设||U0为待分类点的总数目，N′为全局搜索分配

策略分配的点数。IDPCA算法的时间耗费主要表现在四方面：（1）计算各数据点间的距离所需时间为O(N2)。（2）计算 ρ、δ及 γ值所需时间均为O(N)。（3）将待分类点都分配到距其最近的类中心，并获取核心点所需时间为O(NM+N+|U0|)。（4）利用全局搜索策略分配N′个点所需时间为O((N-|U0|+N′)2)，使用统计学习策略分配剩余的N″=N-N″个点所需时间为O(N″2)。因此，IDPCA算法的时间复杂度近似于O(N2)。

4　实验结果与分析

聚类算法的性能通常是采用多种不同测试数据集来验证说明的，本文选取21个不同数据集进行实验。通过与经典聚类算法DBSCAN、K-means、AP及近期提出的DPC算法各项指标的比较，以验证本文算法IDPCA的性能。关于合成和真实数据集的基本属性将于4.2节及4.3节中给出。

文中将聚类算法研究中广为采用的聚类精度（Clustering Accuracyn，Acc）、调整互信息系数（Adjusted Mutual Information，AMI）、调整 Rand系数（Adjusted Rand Index，ARI）这3个指标[17-18]作为聚类算法性能度量标准。其中，Acc与AMI的取值范围均为[]0,1，ARI取值范围为[]

-1,1，各指标值越大，表明聚类质量越高。

实验环境：硬件平台为Intel®Core™i5-6500 CPU@3.2 GHz 3.19 GHz处理器，16.0 GB RAM；编程环境为Win7-Matlab 2015b。

4.1　实验参数分析

本文所提算法包含两个参数：最近邻个数K和相似性系数r。为了分析这两个参数对IDPCA算法聚类质量的影响，本文选取了较为典型的数据集Circle和S2进行实验，其真实分布如图3所示。

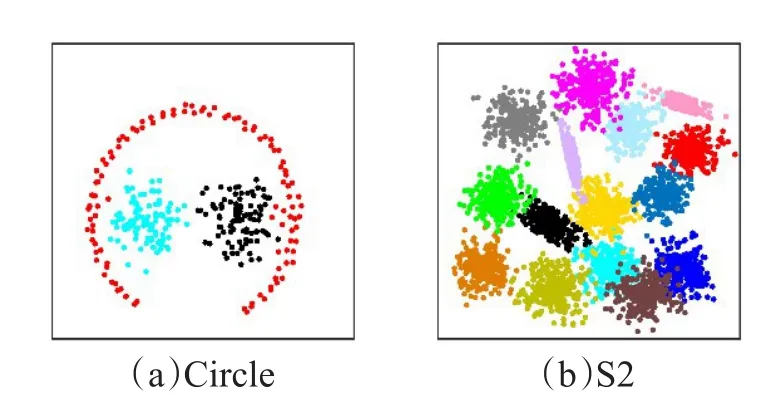
图3　样本数据分布

图4（a）、（b）显示了在Circle数据集上参数 K 和 r对IDPCA聚类质量的影响。当K从3变到4时，对应的聚类精度Acc从76.33%变到99.0%，AMI从53.68%变到95.21%，ARI从48.70%变到96.96%；当K继续增大时，对应的Acc、AMI和ARI呈现下降趋势。当r从0.25变到1时，Acc、AMI和ARI急剧增大，Acc从78.67%变到了99%，AMI从61.45%变到95.21%，ARI从54.27%变到96.96%；而当r继续增大时，对应的Acc、AMI和ARI亦呈缓慢下降趋势。因此，IDPCA算法在Circle数据集上的参数选择为 K=4和r=1。图4（c）、（d）显示了在S2数据集上参数K和r对IDPCA算法聚类质量的影响。当K逐渐增大时，对应的Acc、AMI和ARI也逐渐增大，然后趋于稳定。当r逐渐增加时，各指标值变化相对稳定。由此可知S2数据集对参数K和r不敏感，故IDPCA算法在该数据集上的参数选择可同Circle数据集。

图4　参数对IDPCA算法聚类质量的影响

通过对4.2节和4.3节中其他数据集的数值实验发现：当最近邻数目K=4，相似性系数r在(0,2]区间取值时，均能获得较好的聚类效果。为了便于获取较好的r值，本文依文献[19]的寻优策略，通过网格搜索法进行寻找。该方法将参数区域划分成等距网格，通过遍历所有网格点来寻找使算法性能达到最优的参数。由于网格搜索法在步距足够小的情况下可以在给定区域内找出全局最优解[20-21]，故适用于本文算法IDPCA。文中将参数r所在区间(0,2]划分为步长为0.2的10个网格点，然后遍历每个网格点，选取使聚类结果达到最优的r值。

4.2　合成数据集实验

本节选取12个合成数据集进行实验，各数据集的基本属性如表1所示。

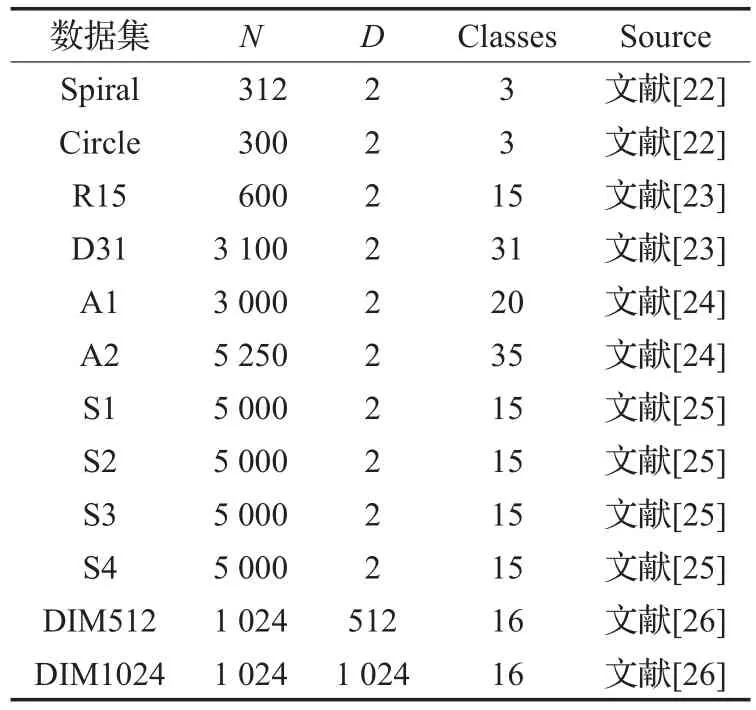
表1　合成数据集

图5和图6分别显示了IDPCA算法与DPC算法对表1中的二维数据集进行聚类所得到的实验结果图，图中不同颜色标识的点对应着不同的类，由黑色“.”标记的点为各算法识别出的聚类中心。

从图5可看出，IDPCA算法不仅能够给出符合直观判断和真实聚类情况的结果，而且能有效处理这10个数据集中所包含的类间重叠、结构复杂以及含有噪声干扰等情况。而在DPC算法的聚类结果中，则明显存在着一些类别误判。例如，对于结构复杂Circle数据集，IDPCA算法仅将外环样本中的两个点错分到内环的类中，而DPC算法却将外环样本中大部分点错分到内环中的类中，主要原因是该算法对剩余点的分配策略会导致误差传播，即一旦有一点错分，那么比该点密度小的点也会被误分。

为了更全面客观地评价IDPCA算法的性能，本文不仅将IDPCA算法与DPC算法作了比较，而且与另外3种经典的聚类算法（DBSCAN、K-means、AP）也进行对比。使用这5种聚类算法对表1中数据集进行聚类所得的Acc、AMI、ARI指标结果见表2，其中粗体数据为最优结果。

对比表2中各聚类算法所获得Acc、AMI和ARI值可发现，这5种算法在DIM512和DIM1024数据集上表现相同，均达到了最优，而对于其他数据集，无论是结构较为复杂的Spiral和Circle，还是数据量较大、含噪声程度不同以及类之间高度重叠的S1～S4，IDPCA均获得良好的聚类效果。

4.3　真实数据集实验

4.3.1UCI数据集实验

为了进一步测试IDPCA算法的性能，从UCI数据库[27]中选取8个真实数据集（如表3）进行实验，以期获得具有指导意义的结果。

图5　IDPCA算法的聚类结果

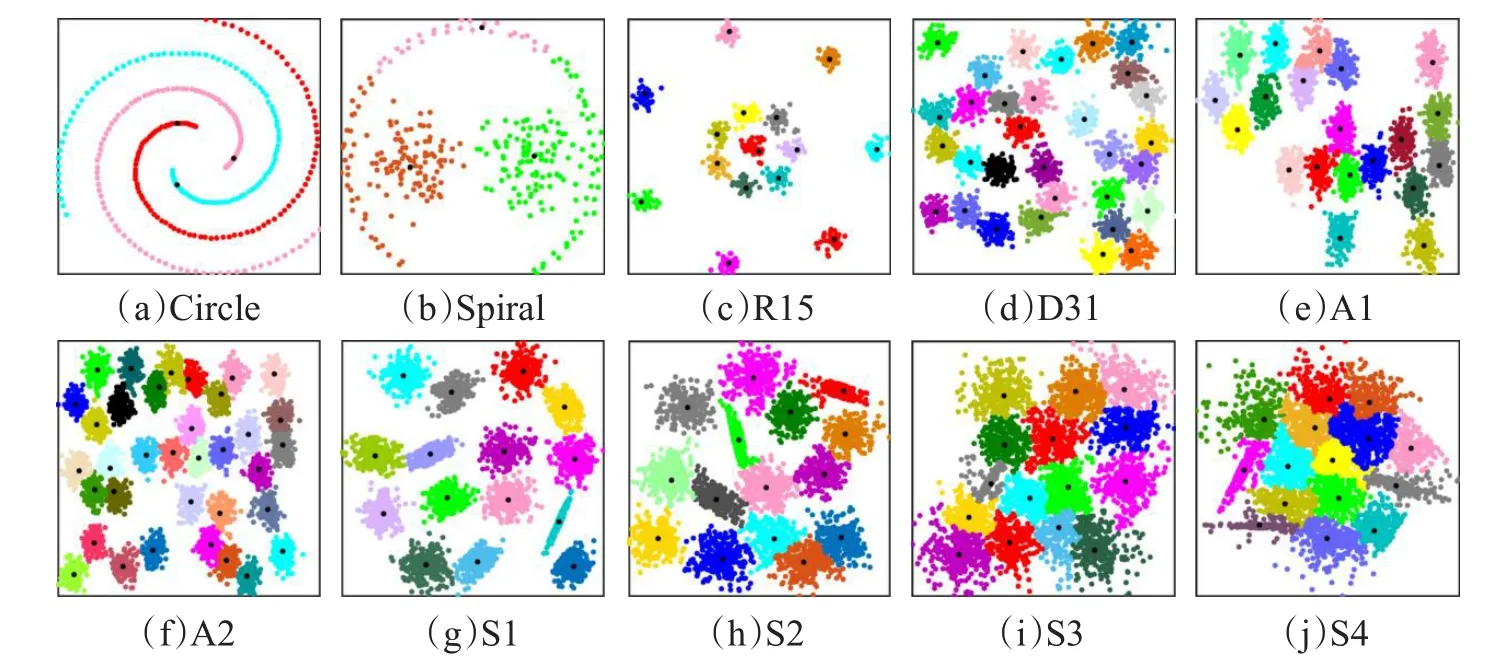
图6　DPC算法的聚类结果

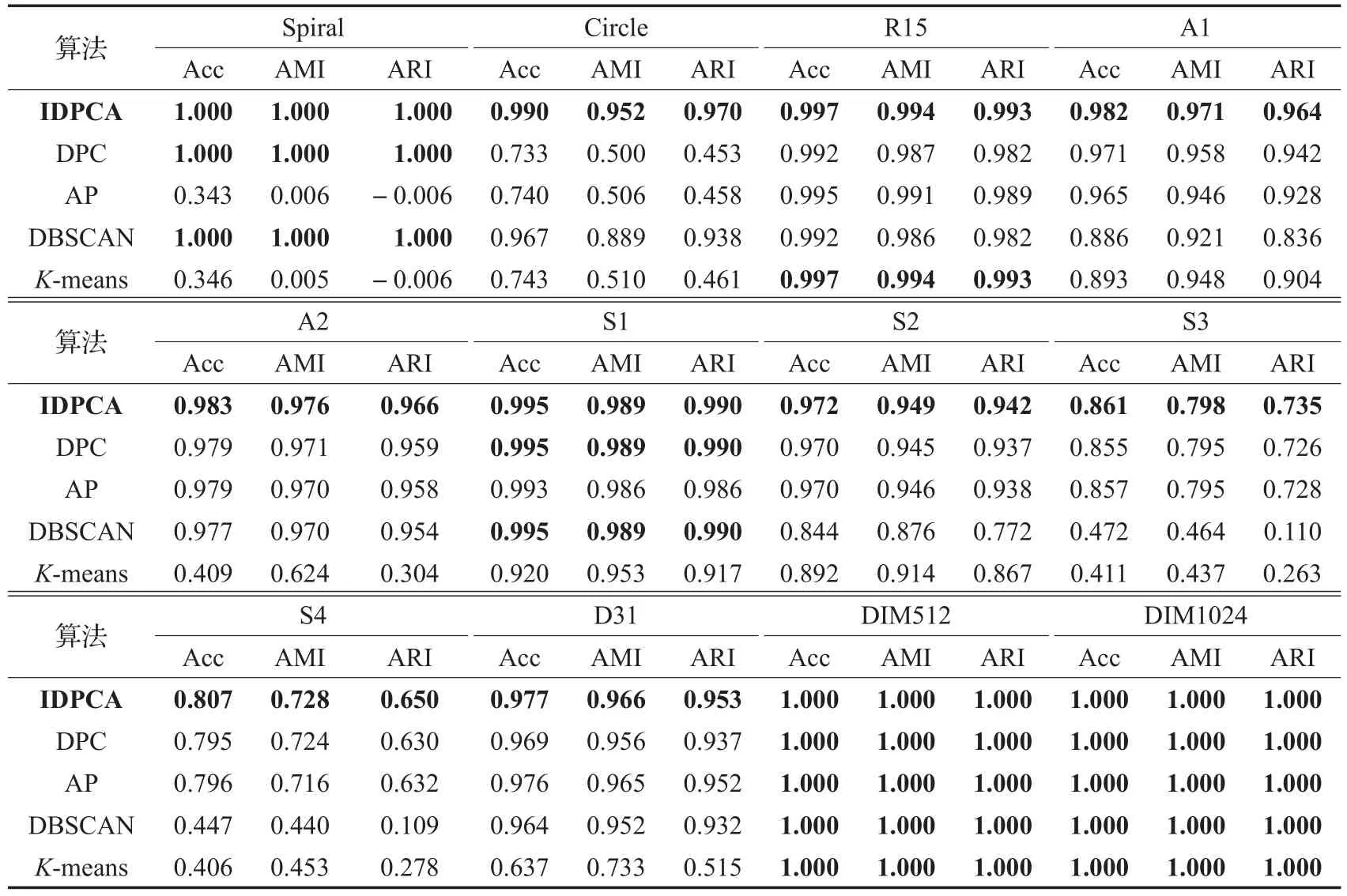
表2　5种聚类算法在合成数据集上的实验结果对比

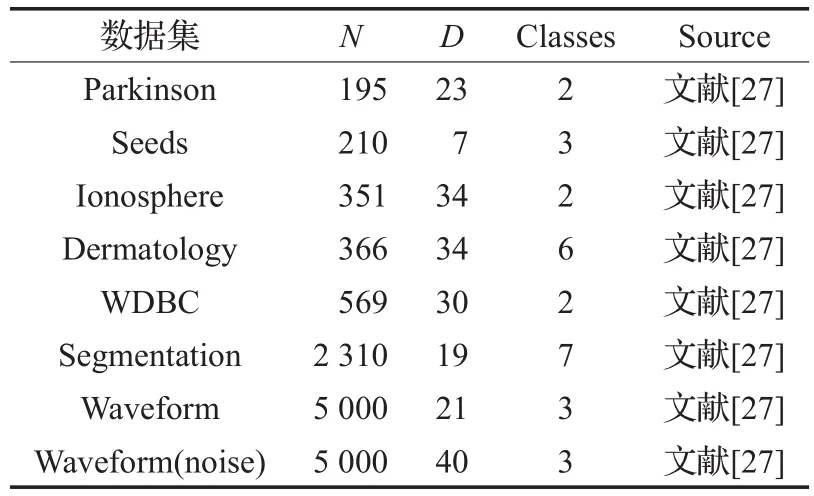
表3　UCI真实数据集

表4显示了IDPCA及其他4种聚类算法对这8个UCI数据集进行聚类所得的Acc、AMI、ARI指标值，其中符号“—”表示无相应值，加粗数据为最优聚类结果。

观察表4可以发现，从AMI和ARI指标看，DPC仅在Ionosphere数据集上获得了最优的聚类结果，K-means算法在Parkinson数据集上获得了最优的AMI结果，而在其余真实数据集上的最优值均由IDPCA算法获得。

4.3.2人脸数据集实验

Olivetti人脸数据集[8]（Olivetti Face Dataset）由40个类组成，每类又包含10幅维数为92×112的人脸图，现已成为测试机器学习算法性能的基准。由于不同类中各图像维数及其相似度都很高，一般算法难以获得理想的聚类效果且计算开销较高，故本节选取该数据集的前10个类（100幅图）进行实验。

使用IDPCA及DPC、DBSCAN、AP、K-means算法对人脸数据集聚类的各指标结果见表5。由于DPC在对该数据集聚类时，选取10个聚类中心会导致包含多个密度峰值的类被分裂成多类，故DPC对该数据集的聚类结果是在选取9个聚类中心时获得的。图7直观显示了IDPCA与DPC在该数据集上的聚类性能，图中不同颜色对应着不同的类，由红色框标识的为错分图，右下角用白色方块标记的图为算法识别出的聚类中心。

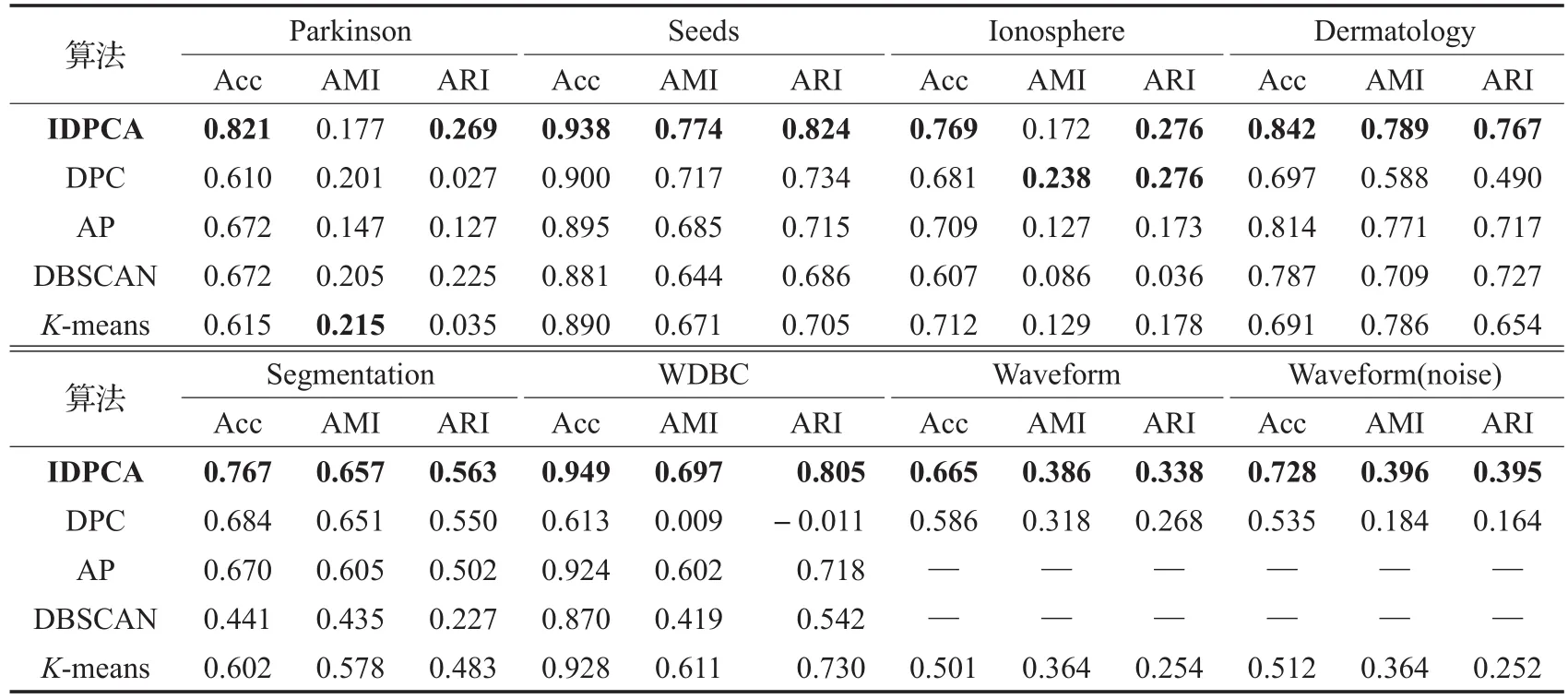
表4　五种聚类算法在UCI数据集上的实验结果对比

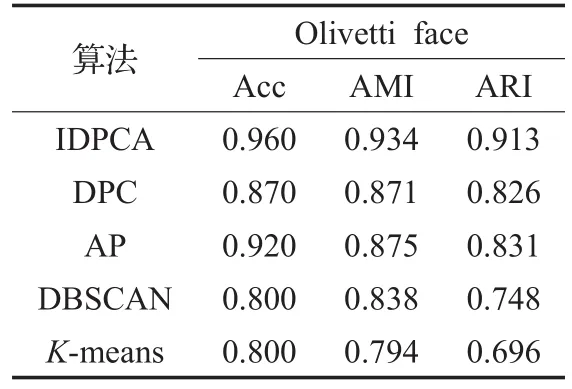
表5　人脸数据集对比实验

图7　人脸数据集聚类对比

对比图7（a）和（b）可以发现，IDPCA有效地识别出了该数据集中的10类，仅分配错4幅图，其主要原因是这些图距其真实类中的图较远，以致它们被分配到真实类的概率值较低，故被归入到其他类，而DPC表现略差。

对比表5中各聚类算法对Olivetti人脸数据集的聚类指标值可知，IDPCA的结果均优于其他对比算法，精度高达96%，AP表现也很好，精度达到了92%，其次是DPC算法。

4.4　算法效率

算法的执行效率通常也是评估其性能的重要指标，本节从时间复杂度方面将IDPCA与DPC、DBSCAN、AP、K-means算法进行比较，并将这5种算法对真实数据集进行聚类所消耗的时间进行对比，以验证其优劣性。

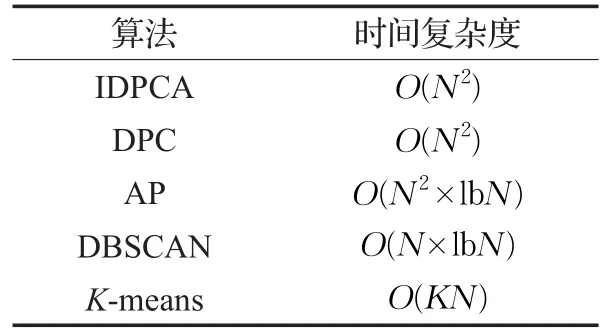
表6　5种聚类算法时间复杂度对比

表6显示了IDPCA及另外4种对比算法的时间复杂度，由该表可知IDPCA与DPC算法的时间复杂度相同，均优于AP，而劣于DBSCAN和K-means算法。表7为5种聚类算法对真实数据集进行聚类所耗时间（均不包括计算距离矩阵或相似度矩阵的时间）。

表7　各聚类算法对真实数据集聚类所需时间s

由表7可知，K-means与DBSCAN算法的运行时间最短，验证了这两种算法具有快速有效的优势。尽管IDPCA与DPC算法的时间复杂度相同，但前者的执行速率略优于后者，而AP的计算开销均高于其他对比算法。

通过不同数据集的聚类实验及算法效率对比实验可知，本文算法IDPCA不仅在聚类精度方面表现较好，其在执行效率方面也略显优势。

5　结束语

面对结构复杂、维数较高及含噪声的数据集，DPC算法仍难以给出符合直观判断并与真实聚类情况相吻合的结果，本文将K近邻与DPC算法思想相结合，提出了一种改进的密度峰值聚类算法。本文算法优点是给出了适用于任意数据集的局部密度计算方法，以及两种不同的剩余点分配策略，不仅减少了误差传播，而且有效提高了聚类效率。通过合成数据集实验表明IDPCA算法能够获得良好的聚类结果，尤其在处理结构复杂的Circle、Spiral数据集以及含噪声程度不同的S1～S4数据集时，其聚类性能在Acc、AMI及ARI方面明显优于DPC、AP、DBSCAN和K-means算法。IDPCA算法在真实数据集上的突出表现及较快的运行速率，进一步验证了其可行性和有效性。

参考文献:

[1]Berkhin P.A survey of clustering data mining techniques[J].Grouping Multidimensional Data，2006，43（1）：25-71.

[2]Xu R，Wunsch D.Survey of clustering algorithm[J].IEEE Transactions on Neural Networks，2005，16（3）：645-678.

[3]Xu D，Tian Y.A comprehensive survey of clustering algorithm[J].Annals of Data Science，2015，2（2）：165-193.

[4]Jain A K，Murty M N，Flynn P J.Data clustering：A review[J].ACM Computing Surveys，1999，31（3）：264-323.

[5]Anil K.Data clustering：50 years beyondK-means[J].Pattern Recognition Letters，2010，31（8）：651-666.

[6]Frey B J，Dueck D.Clustering by passing messages between data points[J].Science，2007，315：972-976.

[7]Ester M，Kriegel H，Sander J，et al.A density-based algorithm for discovering clusters in large spatial databases with noise[C]//Proc of the 2nd International Conference on Knowledge Discovery and Data Mining.Menlo Park：AAAI Press，1996：226-231.

[8]Rodriguez A，Laio A.Clustering by fast search and find of density peaks[J].Science，2014，344：1492-1496.

[9]Wang S，Wang D，Li C，et al.Comment on“Clustering by fast search and find of density peaks”[J].Computer Science，arXiv：1501.04267v2.

[10]Zhang W，Li J.Extended fast search clustering algorithm：widely density clusters，no density peaks[J].Computer Science，2015（5）：1-17.

[11]毋雪雁，王水花，张煜东.K最近邻算法理论与应用综述[J].计算机工程与应用，2017，53（21）：1-7.

[12]周志阳，冯百明，杨朋霖，等.基于Storm的流数据KNN分类算法的研究与实现[J].计算机工程与应用，2017，53（19）：71-75.

[13]Qin C，Song S，Huang G，et al.Unsupervised neighborhood component analysis for clustering[J].Neurocomputing，2015，168：609-617.

[14]Du M，Ding S，Jia H.Study on density peaks clustering based onK-Nearest Neighbors and principal component analysis[J].Knowledge-Based Systems，2016，99：135-145.

[15]Xie J Y，Gao H C，Xie W X，et al.Robust clustering by detecting density peaks and assigning points based on fuzzy weightedK-Nearest Neighbors[J].Information Science，2016，354：19-40.

[16]Liu Y，Ma Z，Yu F.Adaptive density peak clustering based onK-Nearest Neighbors with aggregating strategy[J].Knowledge-Based Systems，2017，133：208-220.

[17]Vinh N，Epps J，Bailey J.Information theoretic measures for clusterings comparison：Is a correction for chance necessary[C]//Proc of the 26th Annual InternationalConferenceonMachineLearning.NewYork：ACM Press，2009：1073-1080.

[18]Vinh N X，Epps J，Bailey J.Information theoretic measures for clusterings comparison：Variants，properties，normalization and correction for chance[J].Journal of Machine Learning Research，2010，11：2837-2854.

[19]Jiang Y Z，Deng Z H，Wang J，et al.Transfer generalized Fuzzy C-Means clustering algorithm with improved fuzzy partitions by leveraging knowledge[J].PR&AI，2013，26（10）：975-983.

[20]王健峰，张磊，陈国兴，等.基于改进的网格搜索法的SVM参数优化[J].应用科技，2012（3）：28-31.

[21]董婷，赵俭辉，胡勇.基于时空优化深度神经网络的AQI等级预测[J].计算机工程与应用，2017，53（21）：17-23.

[22]Chang H，Yeung D Y.Robust path-based spectral clustering[J].Pattern Recognition，2008，41（1）：191-203.

[23]Veenman C，Reinders M，Backer E.A maximum variance cluster algorithm[J].IEEE Transactions on Pattern Analysis&Machine Intelligence，2002，24（9）：1273-1280.

[24]Frant P，Virmajoki O，Hautamaki V.Fast agglomerative clustering using aK-Nearest Neighbor graph[J].IEEE Transactions on Pattern Analysis&Machine Intelligence，2006，28（11）：1875-1881.

[25]Fränti P，Virmajoki O.Iterative shrinking method for clustering problems[J].Pattern Recognition，2006，39（5）：761-765.

[26]Fränti P，Virmajoki O，Hautamäki V.Fast agglomerative clustering using aK-Nearest Neighbor graph[J].IEEE Trans on Pattern Analysis and Machine Intelligence，2006，28（11）：1875-1881.

[27]Bache K，Lichman M.UCI machine learning repository[EB/OL].[2017-11-30].http：//archive.ics.uci.edu/ml.