谐波重构先验信噪比估计算法
王 杰,杨程程,莫嘉永,王敦泽,王谢谢
WANG Jie1,YANG Chengcheng1,MO Jiayong2,WANG Dunze1,WANG Xiexie1
1.广州大学 机械与电气工程学院,广州 510006
2.广州市信息安全测评中心,广州 510635
1.College of Mechanical and Electric Engineering,Guangzhou University,Guangzhou 510006,China
2.Guangzhou Information Technology Security Evaluation Center,Guangzhou 510635,China
1 引言
目前,随着业界对人工智能的日益关注,作为人机接口技术之一的语音信号处理技术得以快速发展。语音增强作为语音信号处理的关键技术的目的是从带噪语音中恢复出纯净语音[1-7]。在单通道语音增强算法中,先验信噪比估计算法已经得到广泛的应用[8-11],较为经典的有Ephraim和Malah提出的极大似然(Maximum Likelihood,ML)估计算法[9]和直接判决(Decision-Directed,DD)算法[2],以及Plapous提出的改进算法(Two Step Noise Reduction,TSNR)[11]。这些算法在一定程度上都取得了较好的消噪效果,但在低信噪比的环境下,增强后的语音信号的高次谐波分量丢失十分严重,从而造成严重的语音失真。为了恢复丢失的高次谐波分量,Plapous等人以先验信噪比估计的维纳滤波法为基础,提出了谐波重构的方法[12],Shen也对此提出了相应的改进算法[13]。
先验信噪比估计算法在较低的信噪比环境下无法准确估计出基音周期是谐波重构的一个难点。已有实验研究表明,对语音信号进行二次谱处理,在时域上可以增大声门激励产生的语音峰值的幅值,即增强语音的浊音信号;在频域上可以使功率谱各谐波峰值更为清晰明显,从而增强了语音信号的周期性[14]。基于此,本文提出了一种基于谐波重构的先验信噪比估计算法。在多种噪声环境下的仿真实验表明,经过谐波重构的先验信噪比估计算法能够有效地恢复谐波分量,提高信噪比,从而改善增强后的语音质量。
2 基于谐波重构的先验信噪比估计算法
2.1 DD算法和Plapous改进算法
假设语音信号模型为y(n)=x(n)+d(n),其中带噪语音y(n)是由纯净语音x(n)和加性噪声信号d(n)相加而获得的。在频域,语音信号模型可以表示为Y(k,l)=X(k,l)+D(k,l),其中 X(k,l),D(k,l)和Y(k,l)分别是x(n),d(n)和y(n)的傅里叶变换,k代表帧数,l代表频率。DD算法的先验信噪比(k,l)可以如下表示[11]:

其中,αDD是常数,典型值为0.92≤αDD≤0.98;GDD(k,l-1)是前一帧的增益函数,(k,l-1)是前一帧的后验信噪比估计值,(k,l)是当前帧的后验信噪比估计值。

其中,βTSNR(k,l)是由DD算法的先验信噪比估计值决定的,如下所示:
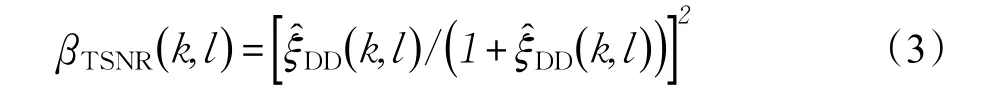
在先验信噪比确定的情况下,Plapous算法和DD算法后续算法步骤是一致的,下面仅考虑DD算法的情况。
带噪语音信号经过DD算法处理后获得增强后的频域语音信号为(k,l):


2.2 二次谱处理
由语音信号的激励模型可知语音信号的浊音部分具有明显的周期性,针对语音信号这一特性,可利用二次谱处理的非线性处理方法来增强语音的谐波分量和周期性。二次谱处理定义如下[14]:
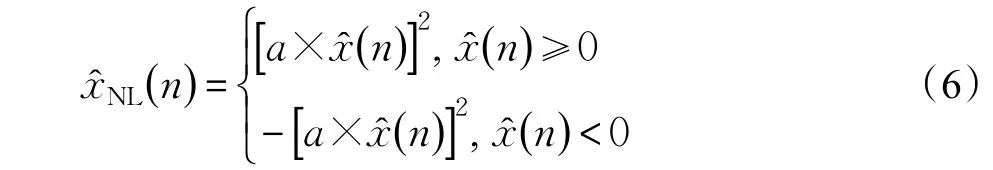
根据文献[15],对式(6)取傅里叶逆变换并取模,得到浊音语音信号的功率谱二次处理如下所示:

从式(7)中可以看出,输入的浊音信号经过二次谱处理后,是一列相关的函数串,且在基音周期处取得最大谱峰[15],即等效于二次谱处理后的浊音信号在基音周期处进行了加权处理,从而增强了语音信号的周期性。
为进一步验证上述结论的有效性,对二次谱处理后的语音信号进行求倒谱运算,结果如图1所示。
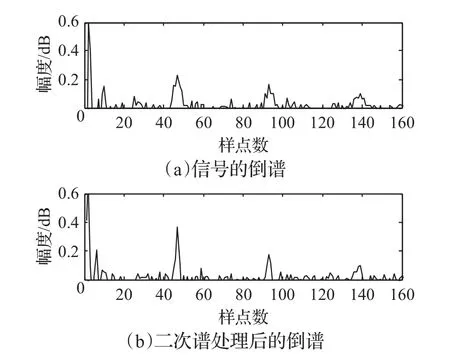
图1 语音信号倒谱和二次谱处理后的倒谱
图1是增强后的语音信号的倒谱和再经过二次谱处理后的倒谱的对比图。根据图1(a)和图1(b)对比可以发现,经过二次谱处理后的语音信号周期处的峰值明显增强,语音信号的谐波峰值更加清晰明显,所以经过二次谱处理增强了语音信号的周期性。接下来将基于此进行谐波重构。
2.3 谐波重构
经过二次谱处理后的语音信号,在增强周期处峰值的同时,也抑制了部分幅值较小的共振峰处的信号;但可以根据浊音信号的谐波结构特性来对丢失的谐波分量进行重构。Plapous提出了一种简单有效的谐波重构算法[12],在这种方法中,对语音信号进行非线性处理,非线性处理函数定义如式(8)所示:

2.4 基于谐波重构的先验信噪比估计算法
通过上述的分析可以知道,改进的谐波重构算法能够有效地增强语音信号的谐波分量,故本节将基于此以DD算法和Plapous改进算法为基础来提升先验信噪比算法的性能,从而提出经过谐波重构的DD-HR算法(DD combining with Harmonic Regeneration,DD-HR)和Plapous-HR算法(Plapous combining with harmonic regeneration,Plapous-HR),以DD-HR算法为例,算法可以分三步来实现。具体步骤如下所示:
(1)通过DD算法对带噪语音信号进行处理,获得增强后的语音信号()k,l。


图2 谐波重构先验信噪比估计流程图
3 实验结果和分析
作为测试样本的纯净语音信号选自Timit Database库;噪声样本选取Noisex-92噪声库的白噪声、Babble噪声和工厂噪声。
语音和噪声的采样频率均为8 kHz,帧长为160,步长为80,其余参数取值:α=0.93,a=5,β=0.84。
如图3是时域波形图的仿真结果,其中(a)为原始语音信号;(b)为信噪比SNR=0的带噪语音信号,几乎将原始语音信号淹没;(c)为DD算法处理后的语音信号,仍然含有一些背景噪声;(d)为经过本文算法处理后的语音信号,可以看出噪声得到进一步的消除,信号成分得到提升。
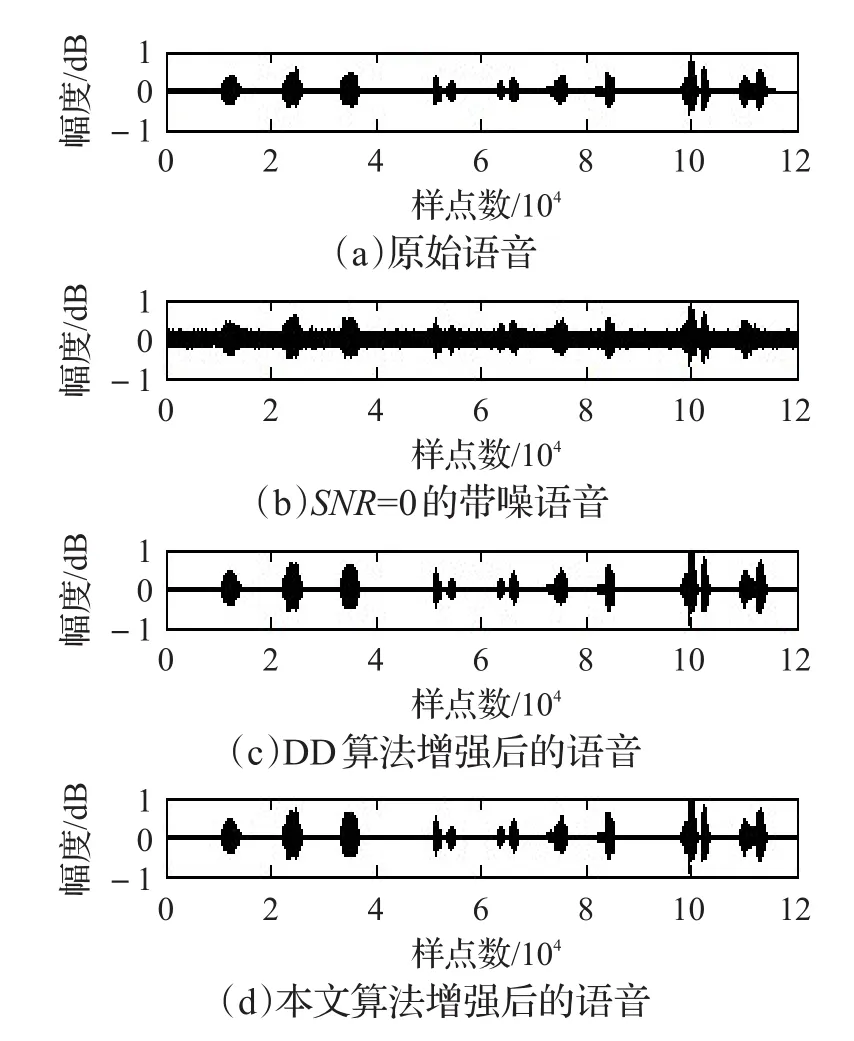
图3 语音信号时域波形图
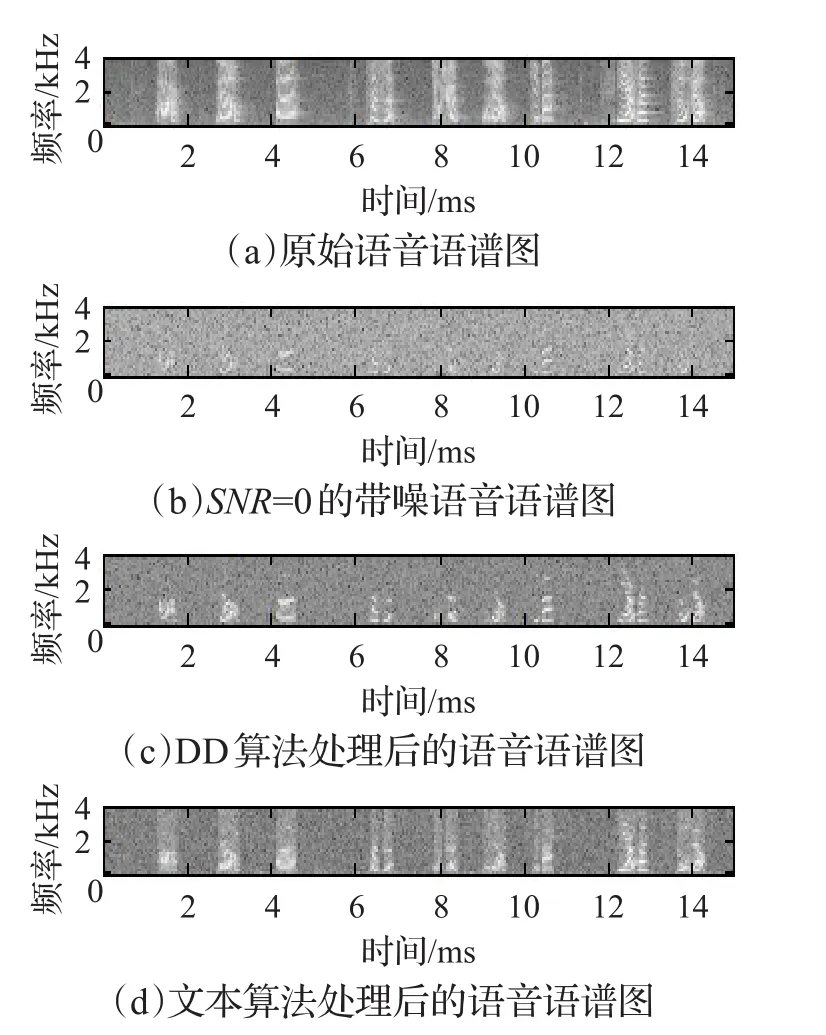
图4 语音信号语谱图
如图4是图3时域波形图对应的语谱图。对比图4中的(c)和(d),可以看出经过谐波重构的DD算法语谱图的条纹更为清晰完善,并且相对于DD算法处理后的语音,高次谐波得到了明显的增强,有效降低了语音失真。
为了进一步验证算法的性能,对算法进行了主客观测试,采用AB测试作为主观测试方法;采用平均段输出信噪比提高量SegSNRI[16]和噪声段的平均噪声抑制量NR[17]作为客观评价指标。
平均段输出信噪比提高量SegSNRI表达式如下式所示:

其中,SegSNRinput是输入语音信号的平均段输出信噪比,L表示语音段的帧数,s为纯净语音信号,ŝ为算法增强后输出的语音信号,且在SegSNRI中,其提高量越高,主观语音质量就会越好。
平均噪声抑制量NR表达式为:

其中,N为语音段的帧数,且在NR中,其抑制量越大,残留的噪声就会少,语音质量就会越好;y为带噪语音信号。
将纯净语音信号加入不同类型的噪声,得到输入信噪比为0 dB、5 dB和10 dB的含噪语音信号,并采用Martin的MS算法估计噪声功率谱[10]。
在主观测试实验中,随机选取Timit Database库中的10段纯净语音,加入白噪声,得到信噪比为0 dB的10段带噪语音,分别利用DD算法、Plapous算法及其相应的改进算法对带噪语音进行处理,从而生成增强后的语音各10组。在AB测试中,定义原算法及其改进算法处理后的语音,测听较优的得“1”分,较差的得“0”分;实验选取听力正常,年龄在22~25岁之间7男3女共10人随机听取原算法及其改进算法处理的共20组语音,并统计测听得分,如表1所示。

表1 改进前后的算法AB测试得分
由表1可以看出,在大多数情况下,经谐波重构改进的算法处理的语音平均得分较高,故在较强的白噪声环境下,本文提出的算法能够提升原算法的性能。
表2给出了四种算法在不同噪声环境下的平均噪声抑制量和平均段信噪比提高量的对比结果。
从表2中可以发现,无论是对于平均输出段信噪比提高量还是对于噪声抑制量,在大多数情况下,经过谐波重构的先验信噪比估计算法(DD-HR和Plapous-HR算法)的性能要优于对应的DD算法和Plapous算法。故本文提出的算法对各类噪声具有较强的鲁棒性,在同等的噪声环境下能够使语音失真较小。
4 结束语
本文以谐波重构算法和先验信噪比估计算法为基础,提出了基于谐波重构的先验信噪比估计算法。该方法在进行语音谐波信号重构之前对语音信号进行二次谱处理,从而增强了语音信号的浊音部分,并突出了语音信号的周期性;然后将谐波增强后的语音信号带入DD算法和Plapous改进算法中以更新先验信噪比并获得相应的增益函数。这样不仅有效地抑制了DD算法和Plapous改进算法中残留的背景噪声,并且增强了语音信号的谐波分量,可以较好地恢复语音信号,减少语音失真。

表2 四种算法的SegSNRI和NR对比
参考文献:
[1]Honesty J,Makino S,Chen J.Speechen hancement[M].Berlin:Springer,2005.
[2]Ephraim Y,Malah D.Speech enhancement using a minimum-meansquare error short-time spectral amplitude estimator[J].IEEE Transactions on Acoustics Speech and Signal Processing,2003,32(6):1109-1121.
[3]Scalart P,Filho J.Speech enhancement based on a priori signal to noise estimation[C]//Proceedings of IEEE International Conference on Acoustics,Speech and Signal Processing,1996:629-632.
[4]熊民权,曾以成,侯丽霞,等.运用MMSE先验信噪比估计进行语音增强[J].计算机工程与应用,2011,47(27):152-154.
[5]姜占才,孙燕,王得芳.基于谱减和LMS的自适应语音增强[J].计算机工程与应用,2012,48(7):142-145.
[6]郑成诗,周崟,李晓东.基于联合语音出现概率的先验信噪比估计算法[J].电子与信息学报,2008,30(7):1680-1683.
[7]郑成诗,胡笑浒,周翊,等.基于噪声谱结构特性的谱减法[J].声学学报,2010,35(2):215-222.
[8]Cohen I.Relaxed statistical model for speech enhancement and a priori SNR estimation[J].IEEE Transactions on Speech and Audio Processing,2005,13(5):870-881.
[9]Cappe O.Elimination of the musicaln oise phenomenon with the Ephraim and Malah noise suppressor[J].IEEE Transactions on Speech and Audio Processing,1997,2(3):345-349.
[10]Martin R.Spectral subtraction based on minimum statistics[C]//Proceedings of European Signal Processing Conference,1994:1182-1185.
[11]Plapous C,Marro C,Scalart P.Improved signal-to-noise ratio estimation for speech enhancement[J].IEEE Transactions on Speech and Audio Processing,2006,14(6):2098-2108.
[12]Plapous C,Marro C,Scalart P.Speech enhancement using harmonic regeneration[C]//Proceedings of IEEE International Conference on Acoustics,2005:157-160.
[13]Shen T W,Lun D P,Hsung T C.Speech enhancement using harmonic regeneration with improved wavelet based a-priori signal to noise ratio estimator[C]//Proceedings of International Symposium on Intelligent Signal Processing and communication systems,2010:1-4.
[14]朱建伟,孙水发,但志平,等.改进的功率谱二次处理基音检测法[J].计算机工程与科学,2010,32(5):140-146.
[15]张天骐,张战,权进国,等.语音信号基音检测的二次谱方法[J].计算机应用,2005,25(4):934-936.
[16]Rix A W,Beerends J G,Hollier M P,et al.Perceptual Evaluation of Speech Quality(PESQ)[C]//Proceedings of IEEE International Conference on Acoustics,Speech and Signal Processing,2001:749-752.
[17]Cohen I.Analysis of two-channel Generalized Sidelobe Canceller(GSC) with post-filtering[J].IEEE Transactions on Speech and Audio Processing,2003,11(6):684-699.

