等级制度下带有时变时滞的群集运动
吴 晨,金英花,石 琳,王世丽
WU Chen,JIN Yinghua,SHI Lin,WANG Shili
江南大学 理学院,江苏 无锡 214122
School of Science,Jiangnan University,Wuxi,Jiangsu 214122,China
1 引言
生活中常常会看到结队成群的鱼群在水中游动时,为了避免相互碰撞,似乎只要感知周围个体的运动情况,而不需要整体的运动状态,即使有些个体有时会偏离鱼群,但能在短时间调整为协调运动的整体,朝着整体运动的方向游动。另外,可以观察到群居的蚂蚁能够在不断变化的环境中,自发组织为一个有效运作的整体,完成所需的工作,这两种自组织的协调运动行为称为群集运动。常见的例子还有编队迁徙的鸟群、聚集的菌落、同步运动的机器人等等[1-6]。群集运动要求所有的多智能体的速度随时间达到一致,且位移差要控制在一定的范围内。由此,群集运动可以看作二阶多智能体系统中一种特殊的一致性问题。生物学、物理学和计算机科学的学者对此做了很多的研究[7-18]。1986年,Reynolds[19]提出了群集运动的三条规则。这三条规则分别是:(1)速度匹配;(2)聚合规则;(3)分离规则。1995年,Vicsek等人[20]在Reynolds研究成果的基础上,在平面上建立了一个经典的离散模型,即Vicsek模型。2007年,Cucker和Smale[21-22]在Vicsek模型的基础上,提出了一个更为一般的群集模型,即C-S模型。在该模型中,每个智能体通过其与其他智能体之间的速度差的加权平均来改变自己的速度。并且他们证明了在参数β<时,无论是连续还是离散的情形,群体会无条件达到群集运动。
可是这个最初的C-S模型并不能模拟等级制度存在的情形,Shen[23]为了解决这个问题,他设计了两个新颖巧妙的方法来分别处理连续和离散的模型。遗憾的是,他仅证明了β<时,连续的模型可以无条件达到群集运动,离散的模型并不可以。
2009年,Cucker和董久刚[24]成功解决了Shen的遗憾,他们证明了在β<时,离散的模型也可以无条件达到群集运动,然而他们都没有考虑通信时滞存在的情形。在实际系统中,由于通信带宽有限,网络会出现通信信道堵塞、信息传递不对称以及信息传递有限等问题,从而产生各类时滞。因此,考虑通信时滞,尤其是时变时滞,是很有实际意义的。所以本文在之前文章的基础上,考虑了通信时滞存在的情形,证明了在等级制度下,当 β<时,离散的C-S模型中即使带有时变时滞,系统仍然能无条件达到群集运动。
2 模型描述
定义2.1一个群体{1,2,…,k}具有等级制度,如果对于所有的x∈Rn,邻接矩阵Ax=(aij(x))满足:
(1)aij≠0暗含 j<i;
(2)对于所有i>1,集合L(i)={j|aij>0}是非空的。
称L(i)为个体i的领导集,称这样的群体为等级群体。
考虑包含k个智能体的二阶系统,第i个智能体的动态方程为:

这里aij(x)表示个体之间的连接强度,满足定义2.1,具体表达形式为:
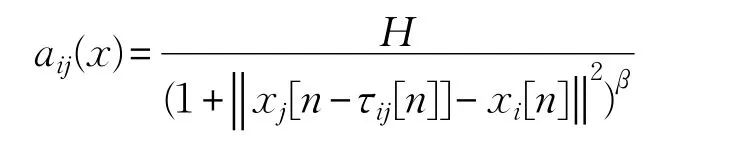
其中,n≥0,xi[n],vi[n]∈R3分别表示为第i个个体在n时刻的位置和速度,τij[n]>0表示在n时刻,智能体i和智能体 j之间的通信时滞,并且规定当n<minτij[n]时,智能体i不受领导集影响,以初始时刻的速度匀速运动,H为耦合系数。
定义2.2对于1≤i,j≤k,若系统(1)中的状态xi[n],vi[n]满足:

则称系统(1)在n→∞时达到群集运动。
3 带有时变时滞的群集运动


则存在P,Q>0,不依赖于n,满足对所有n≥0,成立‖v[n]‖ ≤Qe-Pn。
由等级制度的定义可知,子群体{1,2,…,i-1}的行为是不依赖于个体i的。所以,当子群体{1,2,…,i-1}差不多收敛到一个速度时,等级群体{1,2,…,i}相近于一个由两个个体组成的简单群体,它实际上可以看作是由两个个体的一个扰动。
证明 对子群体{1,2,…,l}来研究,其中l=2,3,…,k,用数学归纳法来证明。
首先,证明结论对子群体{1,2}成立。由等级群体的定义,有L(2)=1,因此a21>0。由于个体1是整个群体的领导者,并且是匀速运动,即v1[n]=v1[n-τij[n]]=v1[0]。




4 数值仿真
本章先考虑智能体之间的没有通信时滞时的收敛情况,与有通信时滞时的情形做比较,之后再通过几个不同的耦合系数,运用数值模拟验证本文结论的正确性。由于在有限时间内,不能达到一致,所以在仿真中如果满足以下条件,就看作达到一致:当t≥t0时,
下面讨论由6个个体组成的多智能体系统式(1),取一组初值,即当 n<minτij[n]时,有:(x[0],v[0])=((105,6),(79,5),(51,8),(61,7),(43,4),(83,11))(其中每个个体都用不同的颜色注明)。
当没有时滞,耦合系数H=4时,观察图1知系统(1)可以实现群集运动,即最终6个智能体速度相等,任意两个智能体的位移差恒定。利用MATLAB仿真求得收敛时刻n0=80。
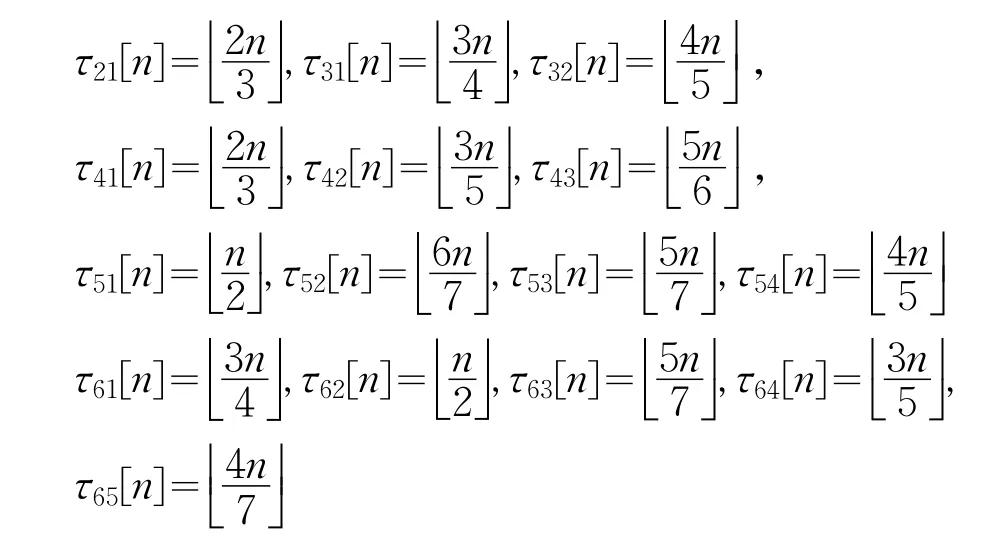
观察图2知系统(1)可以达到群集运动,仿真求得收敛时刻n0=87。
与例1对比可知,当有通信时滞,其他条件不变时,系统实现群集运动所需要的时间变长。由此可以推测,当系统中通信时滞τij[n]满足定理3.1的条件,耦合系数和初值不变时,智能体之间具有通信时滞,系统的收敛特性不变,但收敛速度变长。
例3通信时滞取例2中的函数,耦合系数H=5,时间步长h=0.2,β=(见图3)。
当耦合系数H=5时,观察图3知系统(1)可以实现群集运动,仿真求得收敛时刻n0=73。
与例2对比可知,耦合系数H越大,系统实现一致所需要的时间越短。由此可以推测,当系统中通信时滞和初值相同时,只有耦合系数变化时,耦合系数越大,实现一致的时间越短。


图1 没有通信时滞时,耦合系数H=4,系统达到群集运动的情形

图2 有通信时滞,耦合系数H=4,系统可以达到群集运动

图3 有通信时滞,耦合系数H=5,系统可以达到群集运动
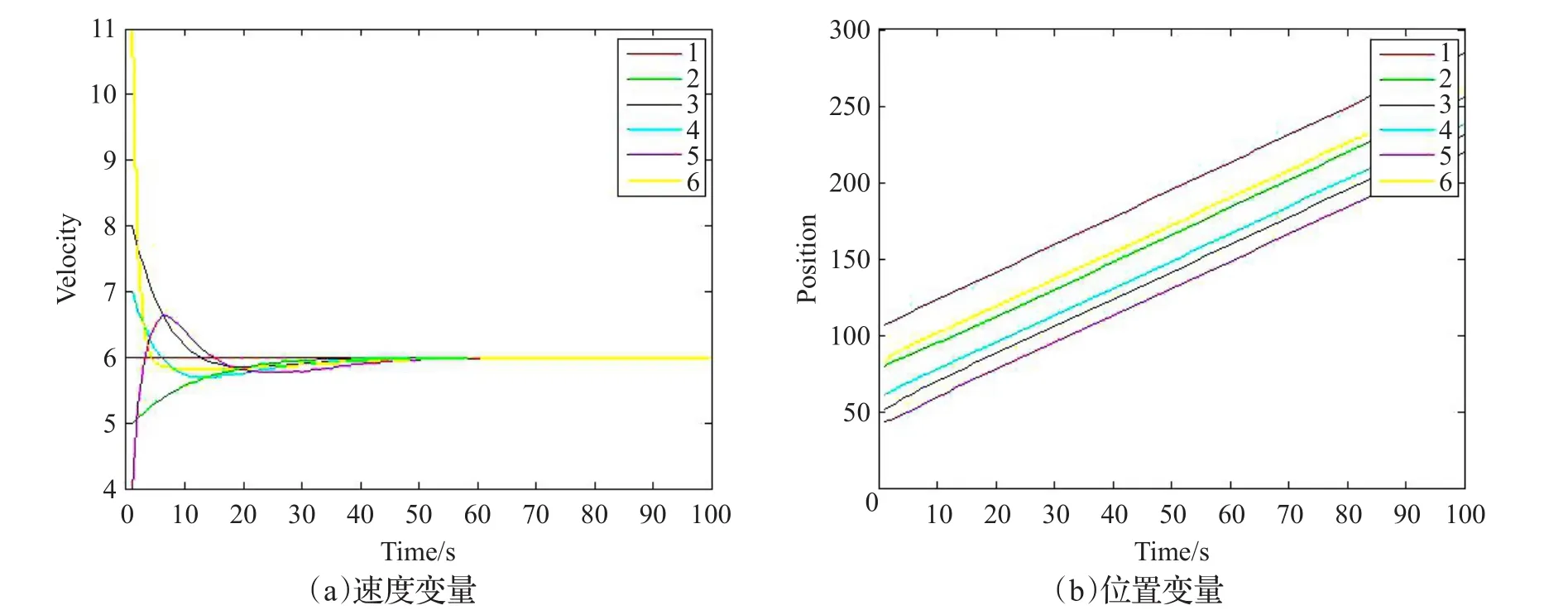
图4 有通信时滞(与例2不同),耦合系数H=4,系统可以达到群集运动
耦合系数H=4,系统可以达到群集运动。
观察图4知系统(1)可以达到群集运动,仿真求得收敛时刻n0=95。
与例2对比可知,例4每一项的时滞函数系数都大于例2。当其他条件不变,通信时滞函数系数变大,系统实现群集运动所需要的时间变长。根据例1、例2和例4可以推测,当系统中通信时滞τij[n]满足定理3.1的条件,耦合系数和初值不变时,智能体之间通信时滞函数系数越大,系统的收敛特性不变,但收敛时间越长。
5 总结
本文对等级制度下离散的C-S模型具有时变时滞的情况进行了分析,给出了系统达到群集运动的充分条件,证明了在β<时,可以无条件收敛,并且利用数值仿真验证了理论结果的正确性。同时通过仿真结果可知,当系统中耦合系数和通信时滞满足定理3.1的条件时,耦合系数越大,系统达到一致的时间越短,通信时滞的变化不影响系统的收敛特性,但会影响收敛速度。本文对β≥的情况未作分析,而且要求全局领导者的速度恒定。然而,在一些实际情况下,领导者的速度可能是变化的,因而对β>的情况,全局领导者速度变化时,还有噪音干扰情况下的分析,将是今后研究的方向。
参考文献:
[1]Fax J A,Murray R M.Information flow and cooperative control of vehicle formations[J].IEEE Transactions on Automatic Control,2004,49(9):1465-1476.
[2]Reif J,Wang H.Social potential fields:A distributed behavioral control for autonoomous robots[J].Robotics and Autonomous Systems,1999,27:171-194.
[3]Feder T.Statistical physics is for the birds[J].Physics Today,2007,60(10):28-30.
[4]Ben-Jacob E,Cohen I,Czirk A,et al.Chemomodulation of cellular movement,collective formation of vortices byswarmingbacteria,andcolonialdevelopment[J].Physica A:Statistical and Theoretical Physics,1997,238(1/4):181-197.
[5]Vicsek T,Czirk A,Farkas I J,et al.Application of statistical mechanics to collective motion in biology[J].Physica A:Statistical Mechanics and its Applications,1999,274(1/2):182-189.
[6]Vollmer J,Vegh A G,Lange C,et al.Vortex formation by active agents as a model for daphnia swarming[J].Physical Review E:Statistical,Nonlinear,and Soft Matter Physics,2006,73(6).
[7]Ru Lining,Li Zhuchun,Xue Xiaoping.Cucker-Smale flocking with randomly failed interactions[J].Journal of the Franklin Insitute,2015,352(3):1099-1118.
[8]Cucker F,Dong Jiugang.A general collision-avoiding flocking framework[J].IEEE Transactions on Automatic Control,2011,56(5):1124-1128.
[9]Dong Jiugang.Flocking under hierarchical leadership with a free-will leader[J].International Journal Robust Non-linear Control,2013,23:1891-1898.
[10]Erban R,Haskovec J,Sun Yongzheng.On Cucker-Smale model with noise and delay[J].SIAM J Appl Math,2015,76(4):1535-1557.
[11]Liu Yicheng,Wu Jianhong.Flocking and asymptotic velocity of the Cucker-Smale model with processing delay[J].Journal of Mathematical Analysis and Applications,2014,415(1):53-61.
[12]Breder C M.Equations descriptive of fish schools and other animal aggregations[J].Ecology,1954,35:361-370.
[13]Grunbaum D,Okubo A.Modeling social animal aggregations[J].Biomathematics,1994,100:296-325.
[14]Okubo A.Dynamical aspects of animal grouping:Swarms,schools,flocks,and herds[J].Adv Biophys,1986,22:1.
[15]Cho J,Ha S Y,Huang F,et al.Emergence of bi-cluster flocking for the Cucker-Smale model[J].Math Mod Meth Appl Sci,2016,26(6):1191-1218.
[16]Cho J,Ha S Y,Huang F,et al.Emergence of bi-cluster flocking for agent-based models with unit speed constraint[J].Analysis and Applications,2016,14:39-73.
[17]Li Z,Ha S Y.On the Cucker-Smale flocking with alternating leaders[J].Quart Appl Math,2015,73:693-709.
[18]Li Z,Ha S Y,Xue X.Emergent phenomena in an ensemble of Cucker-Smale particles under joint rooted leadership[J].Math Mod Meth Appl Sc,2014,24:1389-1419.
[19]Reynolds C W.Flocks,herds,and schools:A distributed behavioral model[J].Computer Graphics,1987,21:25-34.
[20]Vicsek T,Czirok A,Ben-Jacob E,et al.Novel type of phase transition in a system of self-driven particles[J].Physical Review Letters,1995,75:1226-1229.
[21]Cucker F,Smale S.Emergent behavior in flocks[J].IEEE Transactions on Automatic Control,2007,52(5):852-862.
[22]Cucker F,Smale S.On the mathematics of emergence[J].Japanese Journal of Mathematics,2007,2(1):197-227.
[23]Shen J.Cucker-Smale flocking under hierarchical leadership[J].SIAM J Appl Math,2007,68:694-719.
[24]Cucker F,Dong J G.On the critical exponent for flocks under hierarchical leadership[J].Math Mod Meth Appl Sci,2009,19:1391-1404.

