在整合中合理拓展,让思维走向多维
——人教版二下“推理”拓展教学实践与思考
□ 李国娟
《义务教育数学课程标准(2011年版)》中指出:“推理是数学的基本思维方式,也是人们学习和生活中经常使用的思维方式。”推理能力也是学生所应具备的核心素养之一。人教版教材二年级下册“数学广角”专门安排了以“推理”为主题的学习内容,教材设计了例1与例2两个例题、两次“做一做”与一次练习,篇幅虽不多,却承载着培养与提升学生推理能力的重任。但一线教师在执教过程中总会有扑朔迷离的感觉,那么在教学中会遇到哪些问题?如何通过教学培养学生的推理能力?我们从整合与拓展的角度作了拓展尝试,让学生的思维从一维走向多维。
一、“推理”一课教学现状剖析
(一)两例割裂教学,弱化思维提升
在现实教学中,90%的低段教师没有将例1和例2两个例题联系在一起教学,他们认为是孤立分开的,没有将两者打通,就题依题进行教学,所以学生的思维是支离破碎的,无法举一反三。更值得注意的是低段数学教师多是语数包班,他们本身就存在思维的单一以及在教学中多维思维的缺失等问题。如教学“例1有语文、数学和品德与生活三本书,下面三人各拿一本。小刚拿的是什么书?小丽呢?”绝大部分教师喜欢用语言描述推理过程;也有教师考虑到二年级学生年龄较小,光用语言表达不够直观,会借助连线表示;只有小部分教师鼓励学生利用表格行和列的分析帮助学生推理,认识到这种方法不仅直观,还能使每位学生的推理过程更加清晰。但即便使用了“列表法”,教师并不知道将例1(选言推理)和例2(数独)打通的最好方法是“列表法”,从而让学生的思维从一维上升到二维。
(二)思维方式僵化,无法举一反三
在一次数学拓展课程实践专题研讨会上,出示:在下面的方格中,每行、每列都有1~3这三个数,并且每个数在每行、每列中都只出现一次。A应该是几?怎样填?用什么方法?指名某老师(低段数学老师)答:第一行第二个空格数是2,因为第一行应该是1、2、3三个数,现在已经有1、3两个数了;也可以抓住第三列第二个空格数是1……抓住一行一列中都有两个不同的数;也就是在“3×3”的填数中,思考经验为:每行每列上出现两个不同的数,就能填出第三个数。用找准突破口的经验进行解决问题时,尽管同行、同列中数字的特点注意起来了,但是思维还是停留在一维,没有从行与列交叉处进行思考,如第一列与第三行交叉的格子可以填3(第一列与第三行交叉处这个思考突破口一下子找不出来),我们教师的思维也没跳出来……所以必须抓住第一节课例1的列表法分析,让教师有这方面的意识,因为思维力的提升是最重要的。
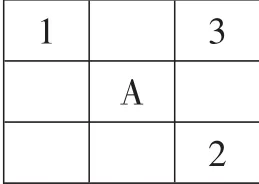
更有许多教师不知道“列表法”与“数独”在“方格、行、列”等组成元素上是相通的;它们在解题方法上都采用“排除法”,可谓是形似神更似,有些教师愈加不领会。
二、拓展教学的理念与尝试
(一)教学理念:注重思维积累,立足从一维走向多维
一维思维,是一种直线的、单向的、单维的、缺乏变化的思维方式,即把认识停留在对事物的抽象而不是本质的抽象,并以这样的抽象为认识出发点的、直线直观的思维方式。尽管线性思维点状化、碎片化,但小学生学习数学的起始阶段这个基础还是要打扎实的。因为把思维过程用线性来进行描述,目的就是为了使原本抽象的思维过程变得更为形象可感,从而使思路更加清晰,使思维更加开阔、更加灵活,再经过长时间的锻炼,进而培养出更为良好的思维习惯,增强思维能力。
而块状思维则是抓住问题的框架结构,形成可以整体迁移的立体的块状思维,以过程思维块、结构思维块、整体思维块呈现的。
基于教材的相通性、解题方法的一致性以及师生的思维现状,有必要增加思维训练,让师生共同成长、发展。于是,我们对教材例1、例2进行了改编,并增设了例3的教学素材。
(二)教学尝试
1.拓展“例1”,渗透列表法推理,初悟思考维度拓展。
(1)教材拓展

上图是原“例1”改编之后的拓展教材,它对原教材中选言、连线的方法进行拓展,在编写时添上了“小精灵推荐的一种列表法”,并在小红这一行、语文这一列交叉的地方打了一个“√”,目的是为让一部分学生能拓宽思维维度。
这样的教材,学生马上能体验到:肯定一项能否定多项,那么,小红这一行、数学这一列交叉的地方只能打“×”;同理:小红不拿品德与生活书以及小丽、小刚不能拿语文书……
(2)教学尝试

?一、游戏教 教 教教教 导学 学 学学学 入内 目 重难环 ,容 标 点点节揭示主题“12学 对1学老师老2..唯..初通小出习 表 不师两师一步结过 用 格上示上门各”学:对推 表 行什语游学上 什教习表断 格 与么文戏科一 么师用格 法 列课课:“,门 叫行表“李行 进 的 。有 学为”格推与 行描 老猜语 科法理列 推述 师一文 ,进”的 理 , 和李猜进 、行,描数方老方进 行推二 述 行有理思达 同验下 , 有序帮思什考桌列序 推助考么表互并思 理学过叫法说用“考“生程推,推推通有因理学理理( 条过为生”自 理分…行编 地享…为拓 进思所展 行考以课 推过…程 理程…教 叙”,材表体述) ,激过使培学用活养生语学学理言生生教解表有线学“述序意性 推推思图理思理考”维过,。进程行通,

续表
将所有已知信息与推理结果呈现在一张表上时,再让学生看看表中信息,进行交流时,就很方便了,如李老师不上语文课,就上数学课;也可以知道方老师上语文课,无形之中将行与列“二维”思维渗透在这里面了,并且感受到了信息与结论的清楚、明白又简洁。让所有学生眼前一亮,立马喜欢上了“表格法”推理。表格呈现信息形象、直观,为培养学生捕捉信息的能力以及语言表达的能力都带来便捷。

李老师方老师语文× √数学√ ×
2.改编“例2”,引入数独法推理,经历多维度思维。
(1)教材改编


本例是基于“列表法推理”的基础上进行创编,通过几个小朋友想象、创造将表格改变成数独的雏形,经历解决“表格中的A是几”这一游戏,使学生的思维有所提升。
为了能够让学生更清楚地表达表格中的某一个格,采用微课的形式,向学生介绍如何去表达以及介绍数独的起源,而本节课的重点在于让学生的思维得到提升,所以,在教学时不要忙于让学生去解决表格中的A是几,而是让学生能够找到突破口,即第一次能填出哪几个数。
(2)教学尝试
这节课以承接例1的表格展开,呈现例1课尾的表格。在这张表格中是带有表头的,即“姓名”与“书本名”。接着教师借“优秀学生”的作品呈现出简化后的表格供学生欣赏,引导学生发现其特殊之处,构建“数独”雏形,为打通“例1”与“例2”教学奠基。将“例1”的表格去除表头、改“√”“×”为数字,即成“数独”,水到渠成。
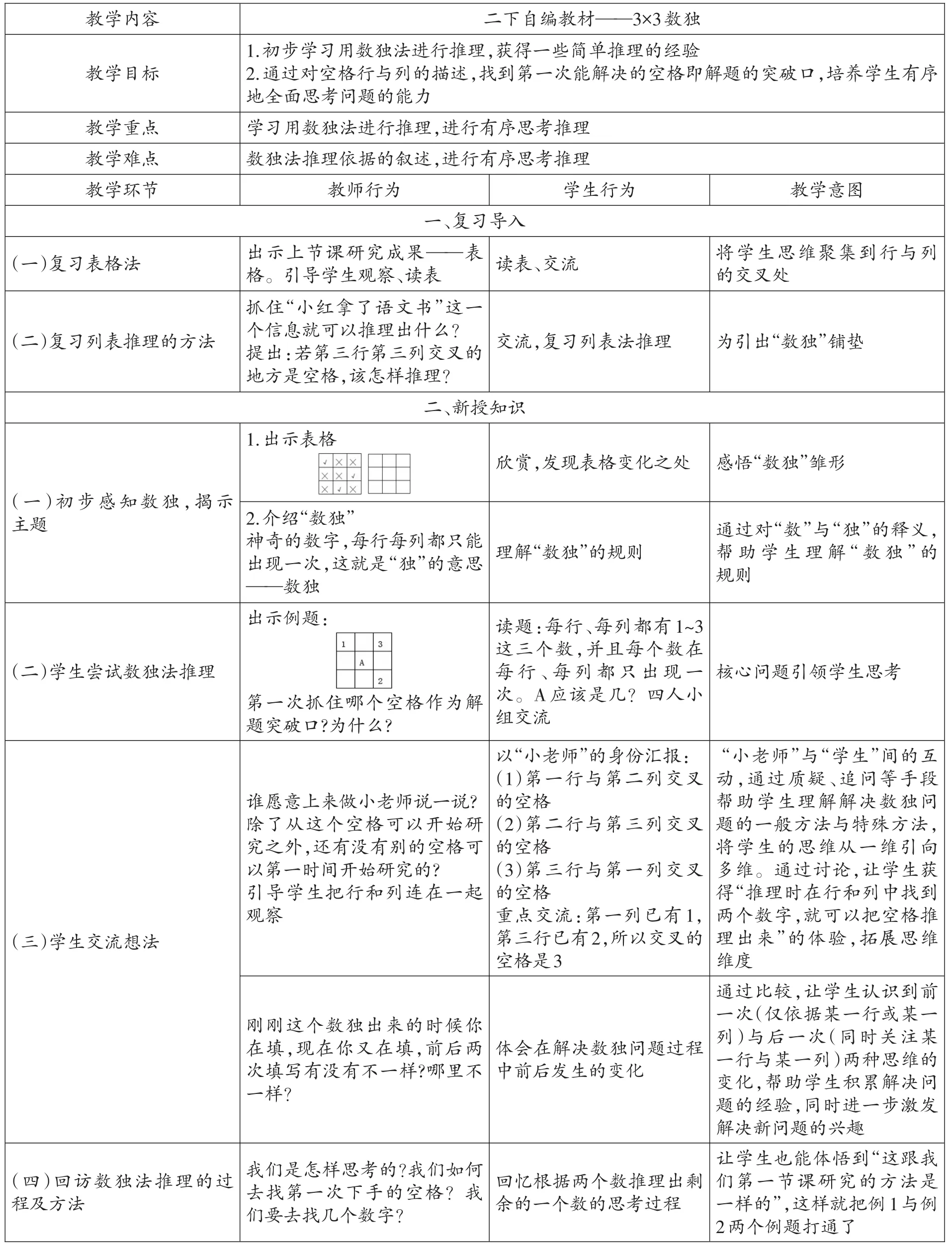
?教学内容 二下自编教材——3×3数独1.初步学习用数独法进行推理,获得一些简单推理的经验教学目标2.通过对空格行与列的描述,找到第一次能解决的空格即解题的突破口,培养学生有序地全面思考问题的能力教学重点 学习用数独法进行推理,进行有序思考推理教学难点 数独法推理依据的叙述,进行有序思考推理教学环节 教师行为 学生行为 教学意图一、复习导入(一)复习表格法 出示上节课研究成果——表 读表、交流 将学生思维聚集到行与列格。引导学生观察、读表 的交叉处抓住“小红拿了语文书”这一(二)复习列表推理的方法 个信息就可以推理出什么? 交流,复习列表法推理 为引出“数独”铺垫提出:若第三行第三列交叉的地方是空格,该怎样推理?二、新授知识1.出示表格(一)初步感知数独,揭示欣赏,发现表格变化之处 感悟“数独”雏形主题2.介绍“数独” 通过对“数”与“独”的释义,神奇的数字,每行每列都只能 理解“数独”的规则 帮助学生理解“数独”的出现一次,这就是“独”的意思 规则——数独出示例题: 读题:每行、每列都有1~3(二)学生尝试数独法推理这每次。三行A个、应每数该列,并是都且几只每 ?出个 四现数 人在一小核心问题引领学生思考第一次抓住哪个空格作为解 组交流题突破口?为什么?以“小老师”的身份汇报: “小老师”与“学生”间的互(1)第一行与第二列交叉 动,通过质疑、追问等手段谁愿意上来做小老师说一说?的空格 帮助学生理解解决数独问除了从这个空格可以开始研(2)第二行与第三列交叉 题的一般方法与特殊方法,究之外,还有没有别的空格可 的空格 将学生的思维从一维引向以第一时间开始研究的?(3)第三行与第一列交叉 多维。通过讨论,让学生获引导学生把行和列连在一起 的空格 得“推理时在行和列中找到观察 重点交流:第一列已有1,两个数字,就可以把空格推(三)学生交流想法 第三行已有2,所以交叉的 理出来”的体验,拓展思维空格是3维度通过比较,让学生认识到前刚刚这个数独出来的时候你 一次(仅依据某一行或某一在填,现在你又在填,前后两 体会在解决数独问题过程 列)与后一次(同时关注某次填写有没有不一样?哪里不 中前后发生的变化 一行与某一列)两种思维的一样? 变化,帮助学生积累解决问题的经验,同时进一步激发解决新问题的兴趣我们是怎样思考的?我们如何 让学生也能体悟到“这跟我(四)回访数独法推理的过 去找第一次下手的空格?我 回忆根据两个数推理出剩 们第一节课研究的方法是程及方法 们要去找几个数字? 余的一个数的思考过程 一样的”,这样就把例1与例2两个例题打通了
“第一次抓住哪个空格?为什么以此作为解题突破口?”教师循循善诱,以这二问为核心问题统领后续教学,扎实有效地开展数独教学,“小老师”汇报时抓住“第三行与第一列交叉的空格”这一思考核心,不断将学生的思维从“一维”引向“多维”。
3.创编“例3”,引入“宫”的教学,提升思维品质。
(1)创编新例题“宫”

宫:由一组被粗线划分的2×2格子围成的区域,用中文数字区分它们的位置,如一宫;
用1~4这4个数字填入以上的方格中,使每一行、每一列、每一宫都有1~4这4个数字,且不重复,B是几?并把四宫数独填完整。

本例是让学生在了解了数独游戏的规则和常用名词(行、列、格)后,在学生原有经验的基础上,全面观察线索,寻找突破口,引导学生重视“宫”,形成块状思维,即只要行、列和宫出现三个不同的数,就能找到“突破口“,从而展开高效的推理过程。这样就使学生的思维更多维,解决数独游戏更简单,激起学生进一步解决数学问题的欲望。
(2)教学尝试

教学内容教学目标二下自编教材——四宫数独1.借助四宫数独,让学生认识和了解数独行、列、宫的基本情况2.通过练习,让学生了解数独宫的游戏规则,会用规则来进行推理

续表
如果说“例2”的教学,学生在思考数独问题时大多是依据“行”与“列”数字的特点,仍有停留在“线性思维”之嫌的话,创编“宫”这一例题并实施教学,则推陈出新,可谓引导学生迈向“多维思维”的利器。
教学之初,学生依旧紧紧抓住“行”与“列”来思考解决问题的突破口。为让学生感悟“宫”的块状思维,教师先让学生通过“摸一摸”“看一看”“选一选”,初步认识“宫”,并将学生的视线慢慢引向盯住“宫”内数字特点不放松,从而使学生的思维聚焦于“宫”,实现“线性思维”迈向“多维思维”的跨越,达成共识后又紧锣密鼓地引导学生依据“宫”内数字的特点尝试“数独”问题的新解法,积累学生解决“数独问题”的经验,提升与拓展思维的深度与广度。
三、“推理”一课拓展教学的价值与反思
(一)用“打通”的眼光妥善处理例1与例2的教学
看似迥异的两个例题实则“貌离神合”。“例1”的选言推理与“例2”的数独法推理看上去是两个独立的例题,一个侧重解决生活问题,另一个是纯粹的数学问题,但“列表法”与“数独法”在“方格、行、列”等组成元素上是相通的;它们在解题方法上都采用“排除法”,而引入“数独”,则顺利搭建了打通例题间教学的桥梁,促思维教学润物无声,进一步突显了“数学广角”的教学价值。
为了打通例1与例2,拓展教学分三步走。

(1)开课就出示例1研究后形成的表格,并要求学生仔细观察表格,找到哪些信息?表格中的小红拿语文书,小丽拿品德书,小刚拿数学书,三人各拿一本书,与题意吻合;为等会儿的“每行每列1~3只能出现一次”打下伏笔。
(2)将第三行第三列交叉处隐去,可以根据表格中的经验推理出来吗?为什么?为引出“行和列已有两个数字,推理空格是(?)”做好认知上的准备。
(3)将表格“演变”成格子以及将标记符号再继续“演变”成行和列9个空格;如果在空格中填上一些有趣的数字就可以进行思维训练了……在这里完成了“表格”与“数独”组成元素的相通性,都有格、行与列;当然随着课堂的深入,让学生感悟到解题方法的一致性,即均用“排除法”。
(二)从“整合”的角度实现学生思维“维度”的拓展
思维按其广度与深度来说具有多个维度,思维的多维性是指能灵活地运用不同的形式和方法,从不同角度去思考问题。多维是敏捷、准确、创造的保证,培养思维的多维性对培养学生优良的思维品质具有核心意义。
此次拓展教学,通过改编与创编例题,借数独穿针引线,将培养学生的推理能力与提升学生的思维维度整合在一起。
如何让学生的思维由“线性思维”上升到“块状思维”,是整合教学中需要关注的重点之一;讲究方式方法达到自觉过渡,就能增强学生的思维体验,从而实现学生思维的多维性。

如右图,教师要求学生独立思考,第一次找到解题突破口的空格是哪一个?理由是什么?先独立思考后与同桌交流再全班指名小老师上台与大家分享,在分享的过程中,让学生经历“宫”的块状思维,并感受到块状思维带来的优势,从而积累如下思考经验:①找到数字最多的“宫”;②兼顾行与列的数字特点;③利用排除法,B填2或3;④一下子就确定“宫”内数字,B为2。

通过此次对“推理”一单元的拓展教学,不仅提升了学生的思维品质,使学生思维更敏捷、更灵活、更高效;同时也转变了教师的教学观念:多揣摩编者的意图,不断地用“打通”“整合”的眼光审视教材,让学生越来越聪明,这必定是每位教师努力追求的目标。

