基于代价的复杂网络边攻击策略有效性分析

王尔申, 王玉伟, 曲萍萍, 蓝晓宇, 陈佳美

(1. 沈阳航空航天大学电子信息工程学院, 辽宁 沈阳 110136; 2. 北京航空航天大学电子信息工程学院, 北京 100191)

0　引　言

现实生活中存在各种各样的复杂网络,这些网络由大量节点和边组成且具有很高的复杂性。其中,节点代表组成该网络中的个体,边代表节点之间的相互联系[1-3]。许多真实网络都可以用加权网络来描述[4-7],如道路交通网络中边的权重可以由两地之间道路的长度或车辆通行所花费的时间来表示。近年来,复杂网络已经得到了社会学[8]、数学[9]、生物学[10]、信息学[11]、军事学[12]与经济学[13]等领域科研人员的广泛关注。

网络的鲁棒性一直是复杂网络研究领域的重要研究方向[14-17]。在很多实际网络中,一个或少数几个节点(边)发生故障后,通过节点之间的耦合关系可能导致整个网络的崩溃,如2003年,美国俄亥俄州由于3条电线烧断引发的北美大规模停电事故[18]。文献[19]在复杂网络鲁棒性方面研究较早,该研究表明,具有无标度特性的网络在随机攻击下表现出较强的鲁棒性,而在蓄意攻击下非常脆弱。文献[20]考虑到网络初始状态和发生故障后可以看作动力学平衡,提出了一个新的级联失效模型,仿真结果表明,对于无标度网络来说,无论是高度节点还是部分低度节点吸收额外负载高于其自身能力,而小世界网络没有这种现象。文献[21]对于复杂网络边袭击策略进行了研究,认为袭击网络中负荷较小的边更易导致相继故障,但是,该研究并没有考虑攻击代价因素。文献[22]对航空公司航线网络的鲁棒性进行了研究,认为低成本航空公司(low cost carriers,LCC)航线网络比提供全方位服务的航空公司(full service carriers,FSC)航线网络更具鲁棒性。在文献[23]中,作者研究了加权复杂网络的动态鲁棒性,认为在异配网络中,低度节点成为关键节点的现象只会出现在弱加权网络和弱耦合网络中,但是该研究只是对节点进行了分析,并没有对复杂网络的边进行分析。文献[24]以自然连通度为网络抗毁性谱测度指标,通过混合择优模型构造不同度分布的复杂网络,研究了度分布对网络抗毁性的影响,研究表明在相同条件下,网络度分布越不均匀,抗毁性越强。

然而,以往的研究大都考虑攻击节点,未考虑攻击代价因素或直接假设攻击代价相同[25-31]。实际上,对许多真实的网络系统进行攻击所花的代价存在很大差异。文献[32]研究了代价下节点攻击策略的有效性,提出了介数紧致系数和接近度紧致系数两个新的度量指标,仿真结果表明,针对同一网络度攻击策略最差;相同平均度下,介数紧致系数或接近度紧致系数越小,则与此接近的介数或接近度攻击策略越有效,但是没有研究代价下边攻击策略。文献[33]研究了在复杂网络节点之间如何有效地分配有限的防御资源,以使得网络在面对各种攻击策略时所遭到的破坏程度降到最小,发现从基于代价的攻击角度看,存在一个最优的防御资源分配策略,可以使得网络得到最大限度的保护,最优防御的配置问题取决于网络参数,网络连接更稀疏可能更有益于网络防御优化。文献[34]对于复杂网络中的攻击策略提出了一种代价约束模型,认为节点度较低的节点在约束代价较高时会优先被攻击,而节点度较高的节点在约束代价较低时才会优先被攻击;除此之外,还发现存在代价敏感型参数阈值,如果攻击单个节点的代价小于这个阈值,那么节点度高的节点不会被优先攻击。文献[35]研究了复杂网络在考虑代价情况下,攻击节点时网络的鲁棒性,但并没有涉及到考虑代价时攻击边的情况。

受之前研究内容的启发,文中主要研究复杂网络边的攻击,并且考虑边的攻击代价因素。假设攻击代价与边的权重呈正相关的关系,提出基于代价的复杂网络边攻击模型,采用边的3种攻击策略对网络进行攻击。研究在考虑攻击代价时分别使用这3种策略攻击边对于普通无标度网络和指数可调无标度网络鲁棒性的影响。

1　基于代价的复杂网络边攻击模型

1.1　无标度网络

20世纪末,Barabasi-Albert(BA)无标度网络模型被提出,真实网络的无标度特性源于两种生成机制:①网络通过增加新节点而持续扩张;②新节点择优连接到具有大量连接的节点上。现实中众多网络具有无标度特性,该网络模型应用非常广泛。该模型的具体算法在文献[2]中有详细介绍。文献[1]中生成了基于配置模型的无标度网络,其指数可调。

文献[3]提出一种生成幂指数可调的无标度网络的算法。设初始网络中包含N个孤立节点,并将所有的节点从1到N依次编号,然后给节点i赋权值pi=i-α,其中,α是一个控制参数。将所有权值加权归一化,即

(1)

从而有

(2)

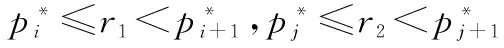
可以证明,根据此算法生成的网络,其度分布满足幂率特性,即P(k)∝k-γ,并且γ满足

(3)

通过调节控制参数α在区间[0,1)内变化,可以生成幂率指数γ在(2,+∞)内的无标度网络。

1.2　边权重的定义

现实中很多网络都是有权网络,一个具体的网络可以由点集V和边集E组成的图来表示,N=|V|为节点数,M=|E|为边数。一般使用权重邻接矩阵w=(wij)n×n表示加权网络边权重。wij表示节点i和节点j连接的边的权重,当网络中各条边的权值都相同时,加权网络即退化为无权网络。边的权重与两个节点的度相关,假设网络的某条边所连两个节点i和j的度值分别为ki和kj,那么这条边的权重可以定义为

(4)

式中,θ(θ>0)是一个可调的权重参数,用于描述所连两节点间联系的强度。

1.3　边攻击策略

以往对于复杂网络鲁棒性的研究大多是基于节点的攻击。边攻击策略的定义是基于边的重要性度量指标,如边的权重,即将边按照其权重的大小进行排序并移除。边攻击策略可以按照边的重要性度量指标攻击网络,采用3种攻击策略,即基于初始图面向边权重的重要性度量指标的攻击。这3种攻击策略定义分别如下:

(1) 边的权重随机攻击策略(random weight removal strategy,RW):将网络生成的边按照其权重大小随机选择进行移除。

(2) 边的权重由小到大攻击策略(low weight removal strategy, LW):将网络生成的边按照其权重由小到大的顺序进行排序,按照此排序结果对边进行移除。

(3) 边的权重由大到小攻击策略(high weight removal strategy, HW):将网络生成的边按照其权重由大到小的顺序进行排序,按照此排序结果对边进行移除。

1.4　网络鲁棒性测度

复杂网络的鲁棒性可以用最大连通子图[15]、平均路径长度[19]和自然连通度[26]等多种指标进行测度。

文中采用最大连通子图相对值S和平均路径长度L两种指标共同来衡量网络的崩溃程度。特别地,对于网络的毁损效应不考虑级联损失。

(1)S定义为被攻击后的网络最大连通子图的规模N′与原始网络规模N的比值,即

S=N′/N

(5)

式中,N′表示相继故障结束后网络的最大连通子图所含的节点个数;N表示初始网络节点数。S的值越大,表示网络的鲁棒性越强。比较网络遭到攻击前后的最大连通子图的相对大小S,可以直观地反映网络遭到攻击与破坏的程度。

(2) 网络的平均路径长度L定义为任意两个节点之间的距离的平均值,即

(6)

式中,N为网络节点数;dij为网络中任意两个节点i和j之间的最短距离。一般来说,平均路径长度越短,网络的连通性越好。

1.5　边攻击代价

关于复杂网络攻击性研究大多基于无代价条件或基于代价时节点的攻击。但是,不同网络节点和边的性质不同,攻击代价是不同的。文中采用边的权重近似衡量攻击代价,即costi=wi。总的攻击代价定义为

(7)

式中,we是边e的权重;M是生成的总边数;Z是移除边的数量总和。

1.6　基于代价的复杂网络边攻击模型算法

根据第1.1节～第1.5节的相关定义,该模型具体算法步骤设计如下:

步骤1按照第1.1节中的算法生成一定规模的BA无标度网络和指数可调的无标度网络。

步骤2按照边的权重式(4)分别求出两种网络中节点之间所连边的权重。

步骤3设定代价初始值,将边按照第1.3节中的3种策略分别进行攻击,将被攻击的边的权重按照式(7)计算ρ值,如果ρ的值比所给代价值小,那么这条边被移除,重复此步骤直到ρ的值达到所给的代价值。

步骤4按照式(5)和式(6)分别计算每种网络遭攻击后的最大连通子图的大小S与平均路径长度L。

步骤5输出结果。

2　实验仿真结果及分析

为了更好地研究考虑代价时边攻击策略的有效性,文中选取BA无标度网络和指数可调的无标度网络分别进行实验。由于模型中权重参数的影响,实验分别基于边权参数θ=1,2,3的不同情况。文中仿真均在复杂网络边攻击后的毁损效应不包含级联损失的情况下进行。每组实验均进行15次,取平均值作为最终仿真结果。

2.1　边攻击代价对BA无标度网络鲁棒性的影响

首先,以BA无标度网络为例,实验中网络参数设置为N=1 000,m=m0=2，其中，N为网络生成的节点总数；m0为初始网络节点数；m为新节点所连接的已存在的节点数。不同边权参数下BA无标度网络鲁棒性随边攻击策略的变化曲线如图1所示。同一攻击策略下边权参数对BA无标度网络鲁棒性的影响如图2所示。

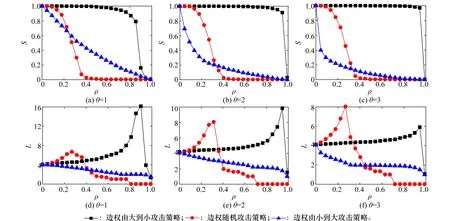
图1　不同边攻击策略对BA无标度网络鲁棒性的影响

图2　边权参数对BA无标度网络鲁棒性的影响

图1为BA无标度网络的鲁棒性随不同边攻击策略的变化曲线图。图1(a)和图1(d)中边权参数θ=1。由图1(a)可以看出,当0<ρ<0.25时,对于同一攻击代价,3种不同边攻击策略有效性由强到弱依次是:LW策略,RW策略,HW策略;当0.25<ρ<1时,对于同一攻击代价,3种不同边攻击策略有效性由强到弱依次是:RW策略,LW策略,HW策略。由图1(d)可以看出,LW策略下,L呈现下降的趋势;而RW策略和HW策略下,L都是先变大,若干次攻击后L才开始下降。当0<ρ<0.25时,LW策略下,网络开始产生孤立的节点,L值开始减小;而采用RW策略或HW策略时,L呈现上升态势,说明这时网络还没有产生孤立节点,但网络的连通性已下降,RW策略对应的网络连通性比HW策略的差,此时3种策略对网络的攻击效率由快到慢依次是:LW策略,RW策略,HW策略。当0.25<ρ<1时,RW策略对应的曲线比LW策略的下降趋势更快,而HW策略下,L值还是先增大后减小,此时3种策略对网络的攻击效率由快到慢依次是:RW策略,LW策略,HW策略。图1(b)和图1(e)中边权参数θ=2。由图1(b)看出,当0<ρ<0.35时,对于同一攻击代价,3种不同边攻击策略有效性由强到弱依次是:LW策略,RW策略,HW策略;当0.35<ρ<1时,对于同一攻击代价,3种不同边攻击策略有效性由强到弱依次是:RW策略,LW策略,HW策略。由图1(e)得知,LW策略下,L呈现下降的趋势;而RW策略和HW策略下,L都是先变大,若干次攻击后L才开始下降。当0<ρ<0.35时,LW策略下,网络开始产生孤立的节点,L值开始减小;而采用RW策略或HW策略时,L呈现上升态势,说明这时网络还没有产生孤立节点,但网络的连通性已下降,RW策略对应的网络连通性比HW策略的差,此时3种策略对网络的攻击效率由快到慢依次是:LW策略,RW策略,HW策略。当0.35<ρ<1时,RW策略对应的曲线比LW策略的下降趋势更快,而HW策略下,L值还是先增大后减小,此时3种策略对网络的攻击效率由快到慢依次是:RW策略,LW策略,HW策略。图1(c)和图1(f)中边权参数θ=3。由图1(c)可以看出,当0<ρ<0.33时,对于同一攻击代价,3种不同边攻击策略有效性由强到弱依次是:LW策略,RW策略,HW策略;当0.33<ρ<1时,对于同一攻击代价,3种不同边攻击策略有效性由强到弱依次是:RW策略,LW策略,HW策略。由图1(f)可以看出,LW策略下,L呈现下降的趋势;而RW策略和HW策略下,L都是先变大,若干次攻击后L才开始下降。当0<ρ<0.33时,LW策略下,网络开始产生孤立的节点,L值开始减小;而采用RW策略或HW策略时,L呈现上升态势,说明这时网络还没有产生孤立节点,但网络的连通性已下降,RW策略对应的网络连通性比HW策略的差,此时3种策略对网络的攻击效率由快到慢依次是:LW策略,RW策略,HW策略。当0.33<ρ<1时,RW策略对应的曲线比LW策略的下降趋势更快,而HW策略下,L值还是先增大后减小,此时3种策略对网络的攻击效率由快到慢依次是:RW策略,LW策略,HW策略。

图2为同一边攻击策略下,可调边权参数对BA无标度网络鲁棒性影响的曲线图。图2(a)和图2(d)中采用LW策略。由图2(a)得知,同一边攻击代价下,θ=3对应的网络曲线下降趋势最快,θ=2对应的曲线次之,θ=1对应的曲线下降趋势最慢。从而,权重参数θ不同取值情况下对网络的破坏顺序:θ=3时对网络攻击效果最好,θ=2次之,θ=1时攻击效果最差。由图2(d)得知,LW策略下,3种θ值对应的L值都呈现减小趋势,说明LW策略下网络较容易产生孤立节点。同一边攻击代价下,θ=3对应的网络L值减小趋势最快,θ=2对应的曲线次之,θ=1对应的L值减小趋势最慢。由此得出,权重参数θ不同取值情况下对网络的破坏顺序:θ=3时对网络攻击效果最好,θ=2次之,θ=1时攻击效果最差。图2(b)和图2(e)中采用RW策略。由图2(b)得知,边权参数不同取值下网络曲线几乎重合,表明设定不同边权参数值对网络破坏效果几乎相同。由图2(e)得知,L值在不同边权参数取值下都呈现先增大后减小的趋势,但趋势几乎一致,表明RW策略下设定不同边权参数对网络毁伤效果几乎相同。图2(c)和图2(f)采用HW策略。由图2(c)得知,同一边攻击代价下,θ=1对应的网络曲线下降趋势最快,θ=2对应的曲线次之,θ=3对应的曲线下降趋势最慢。从而,权重参数θ不同取值情况下对网络的破坏顺序:θ=1时对网络攻击效果最好,θ=2时次之,θ=3时攻击效果最差。由图2(f)得知,HW策略下,3种θ值对应的L值都呈现先增后减的趋势。当0<ρ<0.9时,3种θ值下的L都呈增大趋势,网络连通性由弱到强依次是:θ=1,θ=2,θ=3。当0.9<ρ<1时,θ=1对应的L值开始减小,θ=2与θ=3对应的L值先增后减,θ=2比θ=3的曲线变化明显。

对于BA无标度网络,综合图1和图2的仿真结果可以得知:

(1) 可调边权参数下,HW策略攻击效果都不是最好的;当攻击代价较小时,LW策略的攻击效果最好。

(2) 当采用LW策略时,设置边权参数θ=3时对网络攻击效果最好;当采用HW策略时,设置边权参数θ=1时对网络攻击效果最好。

2.2　边攻击代价对指数可调无标度网络鲁棒性的影响

BA无标度网络度分布的幂率指数γ恒定为3,而大多数具有无标度特性的真实复杂网络的幂率指数在2～3。γ越小,网络在度分布上的非均匀性越强;反之,度分布均匀性越强。选取指数可调的无标度网络进行实验,网络参数设置为N=1 000,m=2,γ=2.4。图3为不同边攻击策略对指数可调无标度网络鲁棒性的影响。 图4为边权参数对指数可调无标度网络鲁棒性的影响。

图3　不同边攻击策略对指数可调的无标度网络鲁棒性的影响

图4　边权参数对指数可调无标度网络鲁棒性的影响

图3为指数可调的无标度网络的鲁棒性随不同边攻击策略的变化曲线图。图3(a)和图3(d)中设置边权参数θ=1。由图3(a)可以看出,当0<ρ<0.3时,对于同一攻击代价,3种不同边攻击策略有效性由强到弱依次是:LW策略,RW策略,HW策略;当0.3<ρ<1时,对于同一攻击代价,3种不同边攻击策略有效性由强到弱依次是:RW策略,LW策略,HW策略。由图3(d)可以看出,LW策略下,L呈现下降的趋势;而RW策略和HW策略下,L都是先增大,若干次攻击后L才开始下降。当0<ρ<0.3时,LW策略下,L值开始减小,网络开始产生孤立的节点;而采用RW策略或HW策略时,L呈现上升态势,说明这时网络还没有产生孤立节点,但网络的连通性已下降,RW策略对应的网络连通性比HW策略的差,此时3种策略对网络的攻击效率由快到慢依次是:LW策略,RW策略,HW策略。当0.3<ρ<1时,RW策略对应的曲线比LW策略的下降趋势更快,而HW策略下,L值还是先增大后减小,此时3种策略对网络的攻击效率由快到慢依次是:RW策略,LW策略,HW策略。图3(b)和图3(e)中设置边权参数θ=2。由图3(b)看出,当0<ρ<0.35时,对于同一攻击代价,3种不同边攻击策略有效性由强到弱依次是:LW策略,RW策略,HW策略;当0.35<ρ<1时,对于同一攻击代价,3种不同边攻击策略有效性由强到弱依次是:RW策略,LW策略,HW策略。由图3(e)得知,LW策略下,L呈现减小趋势;而RW策略或HW策略下,L都是先变大,若干次攻击后L才开始下降。当0<ρ<0.35时,LW策略下,L值开始减小,网络开始产生孤立的节点;而采用RW策略或HW策略时,L呈现上升态势,说明这时网络还没有产生孤立节点,但网络的连通性已下降,RW策略对应的网络连通性比HW策略的差,此时3种策略对网络的攻击效率由快到慢依次是:LW策略,RW策略,HW策略。当0.35<ρ<1时,RW策略对应的曲线比LW策略的下降趋势更快,而HW策略下,L值还是先增大后减小,此时3种策略对网络的攻击效率由快到慢依次是:RW策略,LW策略,HW策略。图3(c)和图3(f)中边权参数θ=3。由图3(c)可以看出,当0<ρ<0.33时,对于同一攻击代价,3种不同边攻击策略有效性由强到弱依次是:LW策略,RW策略,HW策略;当0.33<ρ<1时,对于同一攻击代价,3种不同边攻击策略有效性由强到弱依次是:RW策略,LW策略,HW策略。由图3(f)可以看出,LW策略下,L呈现下降的趋势;而RW策略和HW策略下,L都是先变大,若干次攻击后L才开始下降。当0<ρ<0.33时,LW策略下,网络开始产生孤立的节点,L值开始减小;而采用RW策略或HW策略时,L呈现上升趋势,说明这时网络还没有产生孤立节点,但网络的连通性已下降,RW策略对应的网络连通性比HW策略的差,此时3种策略对网络的攻击效率由快到慢依次是:LW策略,RW策略,HW策略。当0.33<ρ<1时,RW策略对应的曲线比LW策略的下降趋势更快,而HW策略下,L值还是先增大后减小,此时3种策略对网络的攻击效率由快到慢依次是:RW策略,LW策略,HW策略。

图4为同一边攻击策略下,边权参数对指数可调无标度网络鲁棒性影响的变化曲线图。图4(a)和图4(d)中采用LW策略。由图4(a)得知,同一边攻击代价下,θ=3对应的网络曲线下降趋势最快,θ=2对应的曲线次之,θ=1对应的曲线下降趋势最慢。从而,权重参数θ不同取值情况下对网络的破坏顺序:θ=3时对网络攻击效果最好,θ=2次之,θ=1时攻击效果最差。由图4(d)得知,LW策略下,3种θ值对应的L值都呈现减小趋势,说明LW策略下网络较容易产生孤立节点。同一边攻击代价下,θ=3对应的网络L值减小趋势最快,θ=2对应的曲线次之,θ=1对应的L值减小趋势最慢。由此得出,权重参数θ不同取值情况下对网络的破坏顺序:θ=3时对网络攻击效果最好,θ=2次之,θ=1时攻击效果最差。图4(b)和图4(e)采用RW策略。由图4(b)得知,边权参数不同取值下网络曲线几乎重合,表明设定不同边权参数值对网络破坏效果几乎相同。由图4(e)得知,L值在不同边权参数取值下都呈现先增大后减小的趋势,但趋势几乎一致,表明RW策略下设定不同边权参数对网络毁伤效果几乎相同。图4(c)和图4(f)采用HW策略。由图4(c)得知,同一边攻击代价下,θ=1对应的网络曲线下降趋势最快,θ=2对应的曲线次之,θ=3对应的曲线下降趋势最慢。从而,权重参数θ不同取值情况下对网络的破坏顺序:θ=1时对网络攻击效果最好,θ=2时次之,θ=3时攻击效果最差。由图4(f)得知,采用HW策略时,不同θ值对应的L值都呈现先增后减的趋势。当0<ρ<0.9时,3种情况下的L值都呈增大趋势,网络连通性由弱到强依次是:θ=1,θ=2,θ=3。当0.9<ρ<1时,θ=1对应的L值开始减小,而θ=2与θ=3对应的L值先增后减,但θ=2比θ=3的曲线变化趋势明显。

对于指数可调的无标度网络,综合图3和图4的仿真结果可以得知:

(1) 不同边权参数下,HW策略攻击效果较差;当攻击代价较小时,LW策略是最好的攻击策略。

(2) 当采用LW策略时,取边权参数θ=3时对网络攻击效果最好;当采用HW策略时,取边权参数θ=1时对网络攻击效果最好。

3　结　论

文中提出一种基于代价的复杂网络边攻击模型,对考虑代价时BA无标度网络和指数可调的无标度网络的边攻击策略有效性进行了深入研究。研究结果表明:

(1) 边权参数θ取不同值时,采用HW策略攻击效果都不是最好的。现实中在攻击代价较小时,选择相对薄弱的边进行攻击达到的攻击效果较好。

(2) 通过调节权重参数θ,相应的复杂网络边攻击策略攻击效果可以得到优化。

复杂网络边攻击后的网络毁损效应可能包含级联损失,这将是下一步研究的重点。

参考文献：

[1] MOLLOY M R, REED B. A critical point for random graphs with a given degree sequence[J]. Random Structures and Algorithms, 1995, 6(2/3): 161-179.

[2] BARABASI A L, ALBERT R. Emergence of scaling in random networks[J]. Science, 1999, 286(5439):509-512.

[3] GOH K I, KAHNG B, KIM D. Universal behavior of load distribution in scale free networks[J]. Physical Review Letters, 2001, 87(27): 278701.

[4] FENG J, LI X M, MAO B H, et al. Weighted complex network analysis of the Beijing subway system: train and passenger flows[J]. Physica A: Statistical Mechanics and Its Applications, 2017, 474: 213-223.

[5] CHEN Y, WANG X L, XIANG X, et al. Overlapping community detection in weighted networks via a bayesian approach[J]. Physica A: Statistical Mechanics and Its Applications, 2017, 468: 790-801.

[6] WEI D J, CHEN X W, DENG Y. Multifractality of weighted complex networks[J].Chinese Journal of Physics,2016,54(3): 416-423.

[7] WU S Y, SHAO F J, ZHANG Q, et al. Topology association analysis in weighted protein interaction network for gene prioritization[J].Physica A:Statistical Mechanics and Its Applications, 2016, 461: 262-269.

[8] 孙睿,罗万伯.具有非一致传播率的无标度网络谣言传播模型[J].复杂系统与复杂性科学,2014,11(3):6-11.

SUN R, LUO W B. Scale free rumor propagation model with non-uniform transmission[J]. Complex Systems and Complex Science, 2014, 11(3):6-11.

[9] 张兰华. 复杂网络建模的仿真与应用研究[D]. 大连: 大连理工大学, 2013.

ZHANG L H. Simulation and application of complex network modeling[D]. Dalian: Dalian University of Technology, 2013.

[10] BA Q, LI J, HUANG C, et al. Topological, functional, and dynamic properties of the protein interaction networks rewired by benzo(a)pyrene[J]. Toxicology and Applied Pharmacology, 2015, 283(2): 83-91.

[11] ZHANG C M, HUANG H T. Optimal control strategy for a novel computer virus propagation model on scale-free networks[J]. Physica A: Statistical Mechanics and Its Applications, 2016, 451: 251-265.

[12] 徐雪飞, 李建华, 沈迪, 等. 地空多元复杂网络用频优选模型研究[J]. 系统工程与电子技术, 2016, 38(1): 77-83.

XU X F, LI J H, SHEN D, et al. Research of air-ground multi-element frequency optimization model in complex network[J]. Systems Engineering and Electronics, 2016, 38(1): 77-83.

[13] 王楠. 期货时间序列复杂网络特征与投资组合策略研究[D]. 北京: 中国地质大学, 2016.

WANG N. Research on complex network characteristics and portfolio strategy of futures time series[D]. Beijing: China University of Geosciences, 2016.

[14] 张超,张凤鸣,王瑛,等.基于复杂网络视角的航空通信网络鲁棒性分析[J].系统工程与电子技术,2015,31(1):180-184.

ZHANG C, ZHANG F M, WANG Y, et al. Robustness analysis of aeronautical communication networks based on complex network[J]. Systems Engineering and Electronics, 2015, 31(1):180-184.

[15] MOTTER A E, LAI Y C. Cascade-based attacks on complex networks[J]. Physical Review E: Statistical Nonlinear & Soft Matter Physics, 2002, 66(2): 065102.

[16] HONG C, HE N, LORDAN O, et al. Efficient calculation of the robustness measure R for complex networks[J]. Physica A:Statistical Mechanics and Its Applications, 2017,478:63-68.

[17] 陆余良, 杨斌. 域间路由系统级联失效分析与建模[J]. 系统工程与电子技术, 2016, 38(1): 172-178.

LU Y L, YANG B. Analysis and modeling of inter domain routing system cascading failure[J]. Systems Engineering and Electronics, 2016, 38(1):172-178.

[18] 郭东超. 复杂网络拓扑结构的鲁棒性与动力学过程研究[D]. 北京: 北京交通大学, 2014.

GUO D C. Research on robustness and dynamic process of complex network topology[D]. Beijing: Beijing Jiaotong University, 2014.

[19] ALBERT R, JEONG H, BARABASI A L. Error and attack tolerance of complex networks[J]. Nature, 2000, 406(6794): 378-382.

[20] LIU Y Y. Attack vulnerability of complex networks with different initial failure[C]∥Proc.of the 35th Chinese Control Conference, 2016: 1292-1295.

[21] 王建伟,荣莉莉.面向相继故障的复杂网络上边袭击策略研究[J].系统工程学报,2011,26(1): 1-8.

WANG J W, RONG L L. Research on the attack strategy of the complex network with cascading failures[J]. Journal of Systems Engineering, 2011, 26(1):1-8.

[22] LORDAN O, SALLAN J M, ESCORIHUELA N E, et al. Robustness of airline route networks[J]. Physica A: Statistical Mechanics and Its Applications, 2016, 445: 18-26.

[23] HE Z W, LIU S, ZHAN M. Dynamical robustness analysis of weighted complex networks[J]. Physica A: Statistical Mechanics and Its Applications, 2013, 392(18): 4181-4191.

[24] 吴俊, 谭索怡, 谭跃进, 等. 基于自然连通度的复杂网络抗毁性分析[J]. 复杂系统与复杂性科学, 2014, 11(1): 77-86.

WU J, TAN S Y, TAN Y J, et al. Analysis of invulnerability in complex networks based on natural connectivity[J]. Complex Systems and Complex Science, 2014, 11(1):77-86.

[25] WU J, BARAHONA M, TAN Y J, et al. Robustness of random graphs based on graph spectra[J]. Chaos, Solitons & Fractals, 2012, 22(4): 043101.

[26] ESTRADA E, HATANO N, BENZI M. The physics of communicability in complex networks[J]. Physics Reports, 2011, 514(3): 89-119.

[27] 崔文岩, 孟相如, 康巧燕, 等. 基于复合边权重的加权复杂网络级联抗毁性优化[J]. 系统工程与电子技术, 2017, 39(2):355-361.

CUI W Y, MENG X R, KANG Q Y, et al. Optimization of cascading invulnerability on weighted complex networks based on composite edge weight model[J]. Systems Engineering and Electronics, 2017, 39(2): 355-361.

[28] HAO Y H, HAN J H, LIN Y, et al. Vulnerability of complex networks under three-level-tree attacks[J]. Physica A: Statistical Mechanics and Its Applications, 2016, 462: 674-683.

[29] NIE T Y, GUO Z, ZHAO K, et al. New attack strategies for complex networks[J]. Physica A: Statistical Mechanics and Its Applications, 2015, 424: 248-253.

[30] HONG C, ZHANG J, CAO X B, et al. Structural properties of the Chinese air transportation multilayer network[J]. Chaos, Solitons & Fractals, 2016, 86: 28-34.

[31] WANG J W, JIANG C, QIAN J F. Robustness of internet under targeted attack: a cascading failure perspective[J]. Journal of Network and Computer Applications, 2014, 40(7): 97-104.

[32] 覃俊, 吴泓润, 易云飞, 等. 代价下复杂网络攻击策略有效性研究[J]. 北京理工大学学报, 2013, 33(1): 67-72.

QIN J, WU H R, YI Y F, et al. Effectiveness of attack strategies of complex networks with cost[J]. Transaction of Beijing Institute of Technology, 2013, 33(1): 67-72.

[33] WANG X G, GUAN S G, LAI C H. Protecting infrastructure networks from cost-based attacks[J]. New Journal of Physics, 2009, 11(3): 1-9.

[34] DENG Y, WU J. Optimal attack strategy based on limited cost model on complex network[C]∥Proc.of the IEEE International Conference on Systems,Man,and Cybernetics,2015:105-108.

[35] HONG C, CAO X B, DU W B, et al. The effect of attack cost on network robustness[J]. Physica Scripta,2013,87(5):458-465.