Nakagami信道基于16APSK的加权信噪比估计算法

薛　睿, 王　同, 呼德厅

(哈尔滨工程大学信息与通信工程学院, 黑龙江 哈尔滨 150001)

0　引　言

宽带互联网服务需求的快速增长给卫星产业带来了新的挑战。为了满足互联网带宽的需求,大型宽带卫星需要100 Gb的容量[1]。自适应编码调制(adaptive coding and modulation,ACM)技术能够缓解宽带卫星通信中的传播障碍[2],提高宽带卫星通信中无人机数据链的吞吐量[3],是应对这一挑战的重要解决方案。ACM通过检测通信环境的变化,动态地调整编码调制方案,以最优方案匹配此时的信道环境,提高无人机数据链的吞吐量性能。信噪比(signal-to-noise ratio, SNR)是一种衡量信道传输环境好坏的重要参数,SNR估计的准确性直接影响着编码调制方案的选择,因此SNR估计的准确性是决定ACM系统性能的关键因素之一。

SNR估计主要分为时域估计和频域估计两种方法,时域估计可分为数据辅助和非数据辅助两种类型[4]。国内外学者对宽带卫星通信中SNR估计算法进行了大量的研究。文献[5]研究了加性高斯白噪声(additive white Gaussian noise, AWGN)信道下连续相位调制(continuous phase modulation, CPM)信号下的数据辅助与非数据辅助SNR估计算法;文献[6]在此基础上研究了Ka频段卫星通信中基于CPM信号数据辅助和非数据辅助SNR估计算法;文献[7] 基于第二代卫星数字电视广播标准(digital video broadcasting satellite second generation, DVB-S2),提出了一种基于特征值分解的AWGN信道的SNR估计算法;文献[8]提出一种慢时变衰落信道下基于振幅移相键控(amplitude phase shift keying, APSK)的最大似然SNR估计算法,提高了低SNR下的估计精度。

在无人机应用过程中,两种衰落模型可以被考虑应用到其通信数据链中,分别是瑞利衰落信道和Nakagami-m衰落信道[9],m值表示衰落的严重程度,是衡量信道质量的一个重要指标[10]。其中,瑞利衰落主要应用于低空拥挤的区域,Nakagami-m衰落主要应用于高空区域。而大多数无人机都是应用于开放的区域,即高空区域[11]。因此,本文选择Nakagami-m衰落信道作为无人机通信数据链所使用的衰落模型。

目前,针对Nakagami-m衰落信道的SNR估计算法有很多。对Nakagami-m衰落信道进行SNR估计之前,需要对衰落因子m进行估计,文献[10]采用修正因子估计噪声环境下的m参数,提高了低SNR下的估计性能。文献[12]提出了使用接收信号的统计距的非数据辅助SNR估计算法,在低SNR时具有良好的估计性能。文献[13]针对相移键控(phase-shift keying, PSK)和正交振幅调制(quadrature amplitude modulation, QAM)信号,提出基于接收信号包络的概率密度函数的最大似然估计算法,在高SNR时取得了较好的性能。文献[14]在多进制数字相位调制(multiple phase shift keying, MPSK)信号下,提出一种基于阶矩的闭合形式的SNR估计算法,解决衰落因子未知时的SNR估计问题,但只适用于恒包络信号。Nakagami衰落信道下非恒包络信号的SNR估计算法相对较少。本文推导了在Nakagami衰落模型下信号各阶矩之间的关系,在现有算法的基础上进行了改进,提出了一种适用于非恒包络16APSK调制信号的加权SNR估计算法。

1　信道模型

本文以Nakagami衰落信道作为无人机数据链的通信信道模型,信号通过Nakagami衰落信道后[15]可以表示为

rn=αn·sn+ωn

(1)

(2)

式中,m表示形状因子或衰落参数且m≥0.5;Ω=E(α2)表示瞬时功率;Γ(·) 表示Gamma函数。

假设信号经过任意星座图调制后的信号幅度为Ai(i=1,2,…,Q),相应的概率为pi(i=1,2,…,Q)。因此,接收信号的平均SNR定义为

(3)

由文献[15]可知,在衰落因子为αn,发射信号为sn时,rn的包络概率密度函数的表达式为

(4)

式中,I0(x)为第一类修正的零阶贝塞尔函数。

在衰落参数为αn时,接收信号的包络概率密度函数和任意k阶矩的表达式可以分别写为

(5)

(6)

由于衰落因子αn服从Nakagami分布,因此接收信号rn的任意k阶矩可以表示为

(7)

式中,2F1(α,β,γ,x)称作超几何函数,定义[16]为

(8)

式中,(α)n,(β)n,(γ)n的计算方法可统一描述为

(9)

2　基于MPSK调制的SNR估计算法

当信号经过MPSK调制时，由式(3)可知，此时接收信号的平均SNR为

(10)

接收信号的任意k阶矩表达式为

(11)

由于超几何函数F(α)=2F1(α,β,γ,x)具有如下性质[17]:

[γ-2α+(α-β)x]F(α)+α(1-x)F(α+1)-

(γ-α)F(α-1)=0

(12)

利用式(12)可以分别求得F(α)、F(α+1)和F(α-1)的表达式,然后代入式(11),经过推导与化简可得

mMk+2(1+ρ)2+(0.5+1-m)MkM2(1+ρ)ρ-

(k+1)MkM2(1+ρ)(m+ρ)+

(13)

式(13)可以看作是一个一元二次方程,对其进行求解,则SNR估计的表达式[18]为

(14)

从式(14)中可以看出,对于同一接收序列,可以利用任意大于1的k阶矩进行SNR估计。当采用不同的k阶矩进行SNR估计时,所得到的估计值误差也不相同,且所采用的阶矩k越大,SNR的均方误差越大[14],因此本文只考虑k=1和k=2的情况。

当k=2时为二阶矩四阶矩(second and fourth moments, M2M4)SNR估计法,当m=3时SNR估计的解析表达式为

(15)

当k=1时为三阶矩(third-order moments, M3) SNR估计法,当m=3时SNR估计的解析表达式为

(16)

图1和图2分别是MPSK信号的SNR估计性能曲线图和归一化均方误差曲线图,其中,码长为1 152 bit,发送帧数为1 000帧,调制方式为QPSK,衰落参数m为3(若无特殊说明,本文的仿真皆是在m=3的情况下进行)。在蒙特卡罗仿真过程中分别采用 M3 SNR估计法和M2M4 SNR估计法对接收信号进行SNR估计。

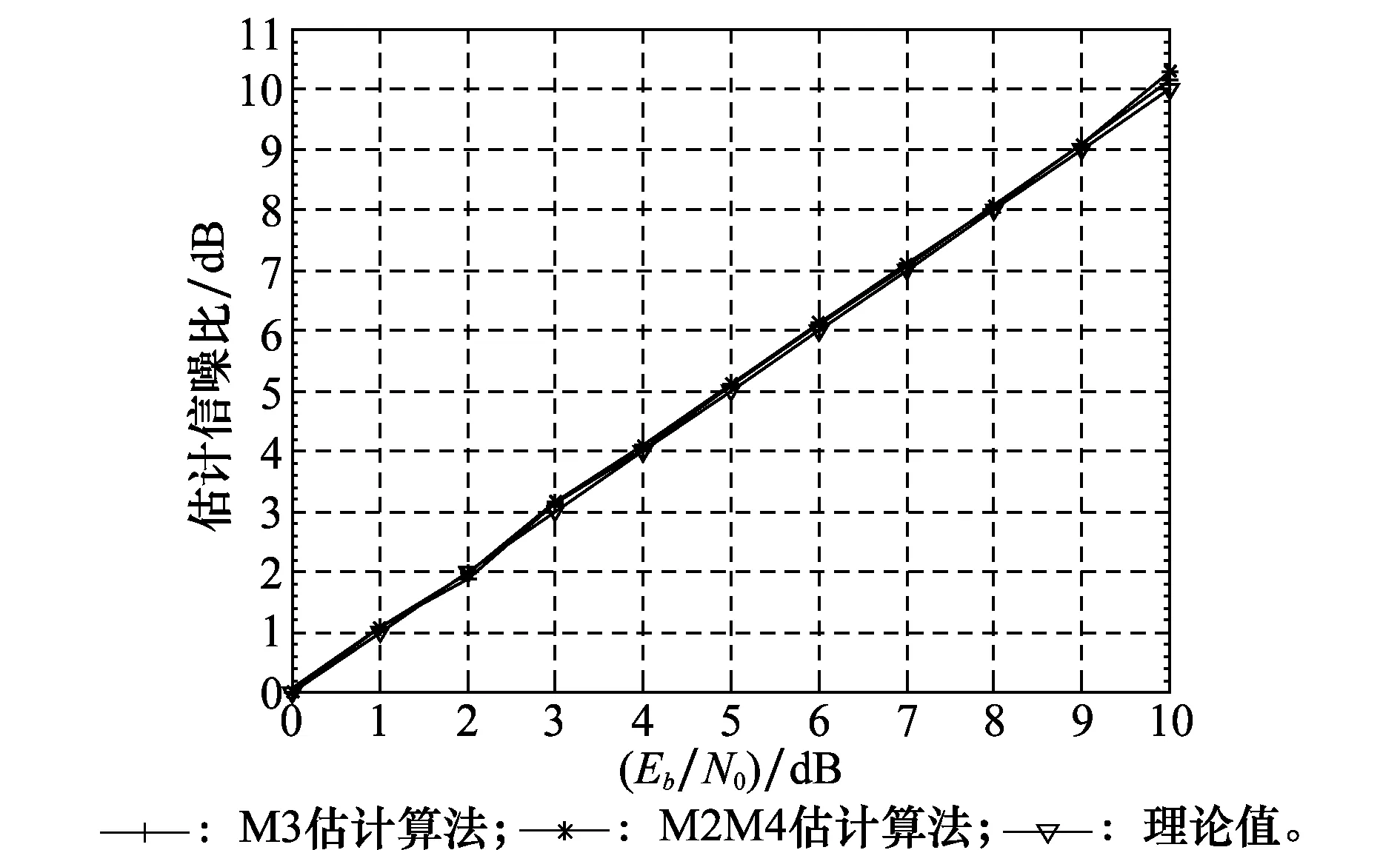
图1　MPSK信号SNR估计性能曲线

从图1和图2中可以看出，在其他条件相同时,M3 SNR估计法比传统的M2M4 SNR估计法具有更好的估计性能,采用M3 SNR估计法得到的估计值更接近理论值,且在SNR较小时,估计值与理论值基本重合。

3　加权SNR估计算法

由图1和图2可知，基于MPSK调制的SNR估计算法在对MPSK信号进行SNR估计时，所得到的估计值与理论值基本重合,取得了很好的估计性能,但是该算法只适用于恒包络调制,对于非恒包络调制信号并不适用。因此本文通过对式(12)进行改进,从而得到了一类适用于对16APSK信号进行SNR估计的加权SNR估计算法。

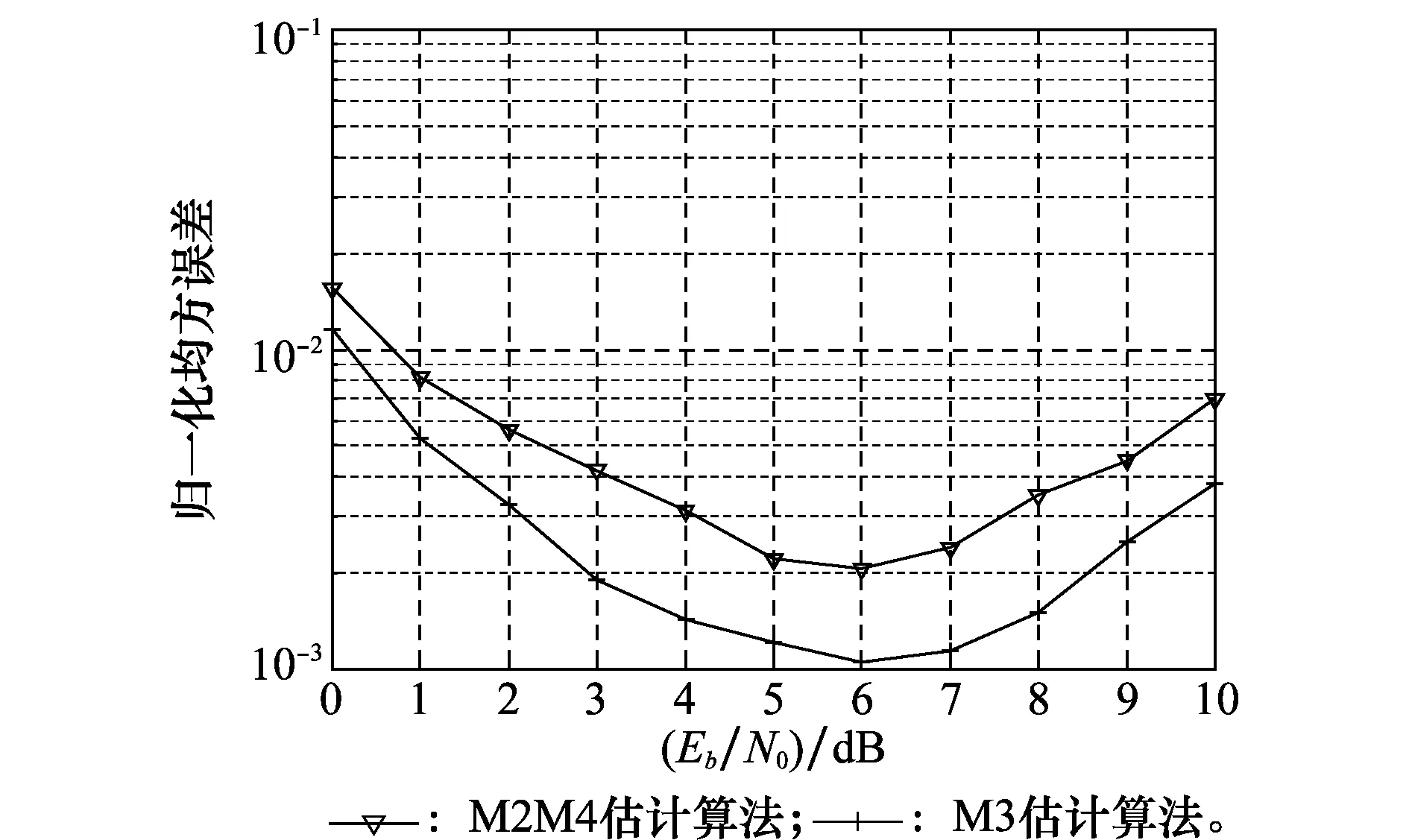
图2　MPSK信号的归一化均方误差

当信号经过16APSK调制时Q=2,16APSK具有不同的星座图,如4+12APSK、10+6APSK以及11+5APSK等,不同的星座图具有不同的映射性能,本文采用性能最优的4+12APSK星座映射方式[19],星座图如图3所示。由图3可知,16APSK信号可看作是由内环的4PSK信号和外环的12PSK信号组合而成,因此由式(3)可知此时估计SNR的表达式为

(17)

图3　16APSK调制信号星座图

由于16APSK调制的内环振幅为A1,外环振幅为A2,因此式(17)可化简为

SNR=p1ρ1+p2ρ2

(18)

(19)

式中,ρ1和ρ2分别是16APSK调制星座图中内环和外环SNR；pi表示信号振幅为Ai的概率。如果能够分别通过计算得到ρ1和ρ2的值以及其前面的加权系数pi,就可以确定16APSK信号的加权SNR。

开发流程为：采用Bootstrap布局对页面进行分割，在分割的不同Div中采用ID选择器对其封装的控件进行调用；在封装时，可对一个Div中要显示的控件进行整体封装；在调用控件时，可对其默认的属性进行设置。具体开发流程见图2。

联立式(8)和式(19)可得16APSK接收信号的任意k阶矩表达式为

(20)

式(20)可以写为

(21)

(22)

(23)

式(22)和式(23)可以分别看作是信号经过4PSK和12PSK调制星座图映射后的接收信号的任意k阶矩,因此,在采用训练序列的前提下,可以按照第2节中的MPSK信道估计方法联立式(19)、式(13)和式(14),从而求得内环SNRρ1,同理可求得外环SNRρ2,其SNR表达式如式(15)所示。由式(15)可知,该加权SNR估计算法是一类利用接收信号包络进行SNR估计的算法,且由第2节以及文献[4]可知,该算法所采用的阶矩k越大,SNR的估计均方误差越大,因此,本文只考虑k=1和k=2的情况。

3.1　加权参数的确定

当采用训练序列对16APSK信号进行SNR估计时,通过统计训练序列符号的振幅分布可以求得p1和p2的值,图4和图5分别是加权SNR算法中k=1时的M3加权SNR估计算法和k=2时的M2M4加权SNR估计算法在不同加权系数时的估计性能。在蒙特卡罗仿真过程中,码长为1 152 bit,发送帧数为1 000帧;在图4和图5的图例中的1/8、1/4、1/2、7/8表示此时加权系数p1的取值。

图4　不同加权系数下的M3加权估计算法的性能

图5　不同加权系数下M2M4加权估计算法的性能

从图4中可以看出,当SNR较高(>8 dB)时,随着加权系数p1的减小,M3加权估计算法的SNR估计值越接近理论值,即SNR估计的估计精度越高;当SNR较低(<4 dB)时,加权系数p1为1/4、1/2、7/8时,估计值与理论值基本重合,而加权系数p1为1/8时,估计误差较大;当SNR在区间[4,8]时,加权系数p1为1/8、1/4、1/2时,SNR估计值与理论值基本重合,而加权系数p1为7/8时,估计误差较大。因此综合考虑整个SNR区间的估计性能,本文选择p1=1/4,p2=1-p1=3/4作为M3加权SNR估计算法的加权系数,结合图3可知,当加权参数p1=1/4,p2=3/4时,加权参数和星座的振幅分布概率相同。

(24)

从图5中可以看出,当加权系数p1为1/2、7/8时,加权M2M4估计算法的SNR估计值与理论值误差较大,SNR估计算法的估计精度较差;当加权系数p1为1/8、1/4时,SNR估计算法的估计精度较高,且与p1=1/8时相比,p1=1/4时的SNR估计算法在SNR小于4 dB时估计精度更高,与理论值基本重合。

为避免仿真参数特殊性带来的影响,在图6和图7中,以码长为576 bit,发送帧数为500帧进行仿真,确定加权参数。

图6　不同仿真参数下M3加权估计算法的性能

图7　不同仿真参数下M2M4加权估计算法的性能

由图6可以看出,加权系数p1=1/4,p2=1-p1=3/4时,SNR估计在整个估计区间都具有很高的精度。p1=1/2,p2=1/2时,SNR估计在整个估计区间都具有很差的精度。p1=1/8与p1=7/8在中等SNR时具有较好的估计精度,而在高SNR或低SNR时具有很差的估计精度。图7中M2M4估计算法在不同加权系数下显示出的性质与图6中M3估计算法性质类似,不再进行具体介绍。由以上分析,综合考虑整个SNR区间的SNR估计性能,本文选择p1=1/4,p2=1-p1=3/4作为M2M4加权SNR估计算法的加权系数。结合图3可知,当加权参数p1=1/4,p2=3/4时,加权参数和星座的振幅分布概率相同。

(25)

3.2　性能分析

图8　16APSK信号SNR估计曲线

图9　16APSK信号的归一化均方误差

为了分析内外环估计SNR对该加权SNR估计算法的影响,图10和图11分别仿真出M3与M2M4加权估计算法的内外环SNR估计值与加权后得到的整体SNR。在仿真过程中,码长为1 152 bit,发送帧数为1 000帧,加权系数p1=1/4,p2=3/4。

图10　M3内外环估计对整体估计的影响

从图10和图11中可以看出,M3与M2M4加权估计算法的外环估计值均高于实际加权估计值,内环估计值均低于实际加权估计值。在低SNR(0～5 dB)时,外环估计值接近实际加权估计值,而内环估计值与实际加权估计值差距较大。内外环估计值均随着SNR的增加，与实际加权估计值差距增大。总体来说,两种估计算法的外环SNR估计值更接近实际加权SNR估计值。

图11　M2M4内外环估计对整体估计的影响

4　结　论

本文首先推导了在Nakagami衰落信道下信号各阶矩之间的关系,然后研究了适用于MPSK调制信号的M3和M2M4 SNR估计算法,在此基础上对该算法进行了改进,得到了一类适用于16APSK调制信号的加权SNR估计算法。该估计算法首先利用M3和M2M4 SNR估计算法求得内环(4PSK)SNR和外环(12PSK)SNR,然后利用加权算法求得接收信号的平均SNR,不同的加权系数具有不同的估计性能,当加权系数的取值与星座的振幅分布概率相同时,加权SNR估计算法具有最佳的估计性能。仿真结果表明,加权SNR估计算法可以有效地对16APSK调制信号进行SNR估计,且具有较高的估计精度。在相同参数条件下,M3加权估计算法的估计误差较小,可以取得比M2M4加权估计算法更优异的估计性能。

参考文献：

[1] HUDSON E. Broadband high-throughput satellites[M]. Berlin: Springer, 2016:1-35.

[2] ROSSI T, SANCTIS M D, RIZZO L, et al. Experimental assessment of optimal ACM parameters in Q/V-band satellite communication[C]∥Proc.of the IEEE Aerospace Conference, 2016: 1-10.

[3] DAI C Q, HUANG N N, CHEN Q B. Adaptive transmission scheme in Ka-band satellite communications[C]∥Proc.of the IEEE International Conference on Digital Signal Processing, 2016: 336-340.

[4] WIESEL A, GOLDBERG J, MESSER H. Non-data-aided signal-to-noise-ratio estimation[C]∥Proc.of the IEEE International Conference on Communications, 2002:197-201.

[5] RICE M. Data-aided and non-data-aided maximum likelihood SNR estimators for CPM[J]. IEEE Trans.on Communications, 2015, 63(11):4244-4253.

[6] XUE R, CAO Y, WANG T. Data-aided and non-data-aided SNR estimators for CPM signals in Ka-band satellite communications[J]. Information, 2017, 8(3): 75-86.

[7] WU H, SHA Z C, HUANG Z T, et al. Signal-to-noise ratio estimation for DVB-S2 based on eigenvalue decomposition[J]. IET Communications, 2016, 10(1):1-7.

[8] LI Z X, YANG D W, WANG H, et al. Maximum likelihood SNR estimator for coded MAPSK signals in slow fading channels[C]∥Proc.of the IEEE International Conference on Wireless Communications and Signal Processing, 2013:1-6.

[9] SIMON M K, ALOUINI M S. Digital communication over fading channels[M]. New York: Wiley, 2000:4-5.

[10] TEPEDELENLIOGLU C, GAO P. Estimators of the Nakagami-mparameter and performance analysis[J]. IEEE Trans.on Wireless Communications, 2015, 4(2):519-527.

[11] ABUALHAOL I Y, MATALGAH M M. Performance analysis of multi-carrier relay-based UAV network over fading channels[C]∥Proc.of the IEEE Globecom Workshops, 2010: 1811-1815.

[12] HAFEZ M, KHATTAB T, SHALABY H M H. Blind SNR estimation of Gaussian-distributed signals in Nakagami fading channels[J]. IEEE Trans.on Wireless Communications, 2015, 14(7): 3509-3518.

[13] NISHIJIMA S, OKA I, ATA S. Maximum likelihood estimation for SNR in Nakagami fading channels[C]∥Proc.of the IEEE International Symposium on Information Theory and Its Applications, 2016: 380-383.

[14] CHANG L, LI G Y, LI J C. Closed-form SNR estimator for MPSK signals in Nakagami fading channels[J]. IEEE Trans.on Vehicular Technology, 2016, 65(9):6878-6887.

[15] DIANAT S A. SNR estimation in Nakagami fading channels with arbitrary constellation[C]∥Proc.of the IEEE International Conference on Acoustics, Speech and Signal Processing, 2007: 325-328.

[16] ANDREWS G E, ASKEY R, ROY R. Special functions[J]. Nature, 2006, 221(226):99-103.

[17] VIOLA C. An introduction to special functions[M]. Berlin:Springer International Publishing, 2016:115-163.

[18] 唱亮, 汪芙平. 一种衰落信道下MPSK信号盲SNR估计的扩展方法[C]∥全国无线电应用与管理学术会议论文集, 2010:581-587.

CHANG L, WANG F P. Generalized blind SNR estimation algorithms for MPSK signals in Nakagami-m fading channels[C]∥Proc.of the National Conference on Radio Applications and Management, 2010:581-587.

[19] KAYHAN F. High order APSK constellation design for next generation satellite communication[C]∥Proc.of the AIAA International Communications Satellite Systems Conference,2016:5735-5743.