半监督稀疏近邻保持投影

吴振宇, 侯冰洋, 王辉兵, 刘胜蓝, 冯　林

(大连理工大学创新创业学院, 辽宁 大连 116024)

0　引　言

随着信息技术的发展,图片、音频等信息采集处理技术进一步提高,人们在日常生活中获得的数据信息维度越来越高,给算法带来难以解决的“维数灾难”问题。在过去的几年中,研究人员构建了很多高效的子空间学习算法,旨在维数约简的过程中,尽可能保持高维数据的某些分布特征,以提高后续分类、聚类以及检索等应用的精度。

传统的线性维数约简方法,如主成分分析(principal component analysis,PCA)[1]、线性鉴别分析(linear discriminant analysis,LDA)[2]易于应用在实际问题中,但这些算法仅仅考虑了样本的全局结构而忽略了不同样本间的局部特征。鉴于此,文献[3-4]提出了局部保持投影方法(locality preserving projections,LPP)和近邻保持嵌入(neighborhood preserving embedding,NPE)等算法,有效地保持了样本之间的局部近邻关系,然而这些无监督算法忽略了全局特征的获取和保持,且不能利用样本标签信息,导致低维子空间判别性能不足。

近年来,基于稀疏表示的稀疏子空间学习已经成为一个重要的研究热点。文献[5]提出了一种稀疏保持投影(sparsity preserving projection,SPP)的降维算法,提高了算法的鲁棒性且降低了算法复杂度。文献[6]提出了一种基于鉴别稀疏保持嵌入(discriminant sparsity preserving embedding,DSPE)的降维算法,通过引入标签鉴别信息,有效地对高维数据进行降维。文献[7]认为稀疏学习有很强的鲁棒性。然而,大多数基于传统稀疏子空间学习方法的问题在于,对高维样本进行稀疏重建时仅考虑了全局信息,没有利用样本的局部特征,不能利用样本的标签信息,容易造成误学习、出现构建样本间错误的相似度关系等问题,这对数据降维十分不利[8-9]。传统监督降维算法通过提取样本的标签信息,避免了无监督算法中的误学习等问题,在分类、识别等实际应用中可取得较好的效果,但标记不足或没有标记的情况下,算法的泛化能力会大大降低,导致分类率急剧下降。在真实世界中,获取有标签样本的代价很高,无标签的数据相对更容易获取,非常容易出现标签数据不足的情况,因此如何改善监督降维算法的泛化性能就变得十分重要。

对于监督学习和无监督学习各自存在的问题,半监督学习技术逐渐成为的研究热点[10-16],半监督学习能够充分地同时利用所有样本(标记样本和无标记样本),改善了监督学习的泛化能力以及提高无监督学习的高效性。基于半监督学习的思想,并针对传统稀疏子空间学习方法存在的问题,提出了一种半监督稀疏近邻保持投影(semi-supervised sparsity neighbouring preserving projections,SSNPP)算法。该算法在保持样本间全局和局部结构关系的同时,又充分利用部分样本的标签信息,大幅提高了子空间的判别能力,在Extended Yale_B、ORL人脸数据集(Olivetti research laboratory，ORL)、AR人脸库上的实验结果验证了该算法的有效性和鲁棒性。

1　SPP算法介绍

1.1　稀疏相关性重构

对于给定的训练集X=[x1,x2,…,xm],其中,xi∈Rn;m>n,每一列是一个样本,稀疏相关性重构希望用训练集中最少的样本来线性重构每一个样本xi,考虑到实际问题中样本存在噪声及数学求解困难等情况,通常在稀疏相关性构造的过程中使用l1约束[10,17],并引入重构误差ε,可通过凸优化进行求解,其目标函数为

s.t. ‖xi-Xsi‖<ε

1=1Tsi

(1)

式中,1=[1,1,…,1]T∈Rm×1;稀疏重构向量si是一列向量，si=[si,1,si,2,…,si,i-1,0,si,i+1,…,si,m]T,其第i个元素是0(表示xi被从X中移除)。

由于约束条件‖xi-Xsi‖<ε的限制,si具有旋转和缩放的不变性;由于1=1Tsi的约束,si具有平移的不变性[5]。另外,由于si中的非零元素大部分对应于同类别的样本,这说明在没有类别标签信息的情况下,si包含了自然的判别信息[6]。

计算每一个xi的稀疏重构向量si之后,可以定义稀疏重构权值矩阵为

(2)

1.2　SPP算法

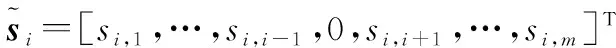
xi=si,1x1+…+si,i-1xi-1+si,i+1xi+1+…+si,mxm

(3)

(4)

(5)

式中,S由式(2)得到。

为了得到更加紧凑的表达式,且为了获得数值稳定性更高的解,式(5)最小化问题可以变换成等价的最大化问题,即

(6)

式中,Sβ=S+ST-STS。

通过拉格朗日乘子法,式(6)进一步转化为广义特征值求解问题，即

XSβXTw=λXXTw

(7)

求前d个特征值的特征向量[w1,w2,…,wd],则SPP的投影矩阵为W=[w1,w2,…,wd]。

2　SSNPP算法介绍

由于稀疏相关性重构的全局特性,导致重构反映出一些错误的样本间关系,为解决此问题,在其基础上利用样本间的局部关系和部分样本的标签信息,构造了稀疏近邻相关性重构,并基于此产生了稀疏近邻保持投影(sparsity neighboring preserving projections,SNPP)。但是SNPP本质上仍属于无监督学习,不能充分利用样本的标签信息,容易造成误学习等,为了进一步提高算法的性能,利用半监督学习的思想,对标签判别信息和稀疏近邻相关性重构信息进行融合,提出了SSNPP算法。

2.1　稀疏近邻相关性重构

由于稀疏表示的全局特性,无法充分利用样本间的局部结构信息,导致传统稀疏降维算法(如SPP等)的重构权值矩阵反映出一些样本间错误的关系。为了解决上述问题,在稀疏重构中的过程中,充分提取样本间的局部结构信息,并利用部分样本的标签信息,把训练集X=[x1,x2,…,xm]∈Rn×m用XDi来代替,其中,Di∈Rm×m是一个对角矩阵,对角元为0或1,Di的引入使得XDi中只包含样本xi的近邻样本和属于同类的样本,其他对于重构无关的样本和噪声样本将被忽略。

为了得到Di,首先计算xi与训练样本集X中的其他样本的欧氏距离,然后从中选出k个最近邻的样本,得到由xi的k个最近邻样本组成的集合为

G(xi)={xi1,xi2,…,xik}

(8)

由于距离近的样本更可能来自同一类,参与重构的相关性会较高,所以在矩阵Di中对应于这些样本的对角元置为1;而与原属于同一类的样本,参与重构的相关性也较高,在矩阵Di中相应的对角元也置为1;其余对角元均为0,表示为

Di=diag(di1,di2,…,dim)

(9)

其中

j∈(1,m)且j≠i

用XDi中的样本来重构xi,通过最小化问题寻找样本xi的最优稀疏近邻相关性重构向量si,表示为

s.t. ‖xi-XDisi‖<ε

1=1Tsi

(10)

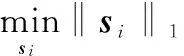
2.2　SNPP算法

类似于SPP利用稀疏相关性保持进行降维,SNPP基于稀疏近邻相关性保持进行降维,为了将高维空间中的稀疏近邻重构关系以最优的结果保持到低维嵌入子空间中,使得在低维空间中样本的稀疏重构误差最小,假设w是SNPP的投影向量,则wTXDisi表示样本xi经过稀疏近邻重构并降维后的低维表示,定义求解出能最优保持si的投影向量w的目标函数为

(11)

式中，X=[x1,x2,…,xm]∈Rn×m是训练集；Di由式(9)求得；si由式(10)求得。

为了便于计算和降低空间复杂度,将式(11)通过代数变换和分块矩阵的乘法处理,得到紧凑的表达形式为

(12)

其中

(D1s1,D2s2,…,Dmsm)∈Rm×m

同样为了防止解的退化,并获得唯一的最优解,引入约束条件wTXXTw=1,则式(12)可以改写为最优化问题，即

(13)

同样为了得到更加紧凑的表达式,且获得更为稳定的数值解,将式(13)最小化问题转化成等价最大化问题,即

(14)

式中,Pα=P+PT-PTP。

式(14)可转化为广义特征分解问题，即

XPαXTw=λXXTw

(15)

求前d个特征值的特征向量[w1,w2,…,wd],组成最优的投影矩阵W=[w1,w2,…,wd]。

2.3　SSNPP算法

在真实世界中,高维数据通常只有一少部分是标记样本,大部分是无标记的数据,无监督维数约简方法很难利用标签信息,导致算法性能低于监督或半监督算法,而SNPP本质上也是无监督降维算法,这就限制了SNPP算法的性能和适用范围。因此,为了充分利用样本的标签信息,本小节利用半监督技术把SNPP算法拓展到SSNPP算法。

对于训练集X=[x1,x2,…,xm]∈Rn×m中分别属于k类的n个有标签的样本组成的子集合XcX,Ai表示第i类样本构成的集合,Ni表示属于第i类样本的个数,mi表示第i类样本的均值,m表示所有样本的均值,计算类间离散度矩阵Sb和类内离散度矩阵Sw为

(16)

(17)

利用最大间距准则(maximum margin criterion,MMC)算法的最大边界思想,使得高维数据降维后,在低维流形中相同类别的样本尽可能靠近,不同类样本尽可能远,从而低维空间的样本为分类做了很好的预处理,使数据具有最大的可分性,目标函数为

max(tr(Sb)-tr(Sw))

(18)

SSNPP算法一方面保持全部样本间的稀疏近邻相关性(式(14)),另一方面提取部分样本的标签信息(式(18)),假设投影向量为w,可以构造出多目标优化函数为

s.t.wTXXTw=1

(19)

为了获得紧凑的形式,把多目标优化问题转换成正则化优化问题来求解,即

(20)

式(20)通过正则化参数λ来融合稀疏近邻重构信息和标签判别信息,使得算法在保持样本间稀疏相关性的同时,充分提取了部分样本的标签信息。

式(20)可以进一步转化为广义特征分解问题，即

(XPαXT+λ(Sb-Sw))w=λXXTw

(21)

通过求式(21)的广义特征分解,得到最大的d个特征值对应的特征向量[w1,w2,…,wd],组合后得最优的投影矩阵W=[w1,w2,…,wd]。

2.4　算法基本步骤

2.4.1SNPP算法步骤

对于兼有标签样本和无标签样本的训练集,基于稀疏近邻相关性重构,求出其最优投影矩阵的SNPP算法步骤归纳如下:

步骤1根据式(8)和式(9)构建出对应于训练集X的对角阵Di=diag(di1,di2,…,dim)。

步骤2利用式(10)计算出对应于各个样本xi的最优稀疏近邻相关性重构向量si。

步骤3矩阵P=(D1s1,D2s2,…,Dmsm)由式(12)计算得出,矩阵Pα=P+PT-PTP由式(14)计算得出。

步骤4求解式(15)的广义特征分解问题,选取最大的d个特征值对应的特征向量,构成最优的投影矩阵W=[w1,w2,…,wd]。

2.4.2SSNPP算法步骤

对于兼有标签样本和无标签样本的训练集,基于稀疏近邻相关性重构,并利用半监督学习技术融合标签样本的判别信息和无标签样本中判别信息,求出最优投影矩阵的SSNPP算法步骤归纳如下:

步骤1根据式(8)和式(9)构建出对应于训练集X的对角阵Di=diag(di1,di2,…,dim)。

步骤2利用式(10)计算出对应于各个样本xi的最优稀疏近邻相关性重构向量si。

步骤3矩阵P=(D1s1,D2s2,…,Dmsm)由式(12)计算得出,矩阵Pα=P+PT-PTP由式(14)计算得出。

步骤4对有标签的训练样本集Xc,由式(16)和式(17),计算出类间离散度矩阵Sb和类内离散度矩阵Sw。

步骤5求解式(21)的广义特征分解问题,选择前d个最大的特征值对应的特征向量,构成最优的投影矩阵W=[w1,w2,…,wd]。

3　实验结果及分析

为验证算法的有效性,在Extended、Yale_B、ORL和AR数据集上进行了实验,同时为客观的评价本文提出的SNPP和SSNPP算法的有效性,引入PCA、NPE、LPP、SPP作为对比算法,利用这6种降维算法分别对3个数据集进行降维,然后统一用最近邻分类器对降维后数据进行分类,以分类的准确率为指标来衡量降维算法的性能。

3.1　实验数据集

本文选择了3个高维人脸数据集,分别是:

(1) Extended Yale_B人脸数据集,含有38组正面的人脸图像,每组包括59副人脸图像,共2242副人脸图像,图像的像素是32×32,这些图像之间的区别是不同的光照条件和面部表情等。

(2) ORL含有40组正面的人脸图像,每组包括10副人脸图像,共400副人脸图像,图像的像素是32×32,这些图像之间的区别是不同的光照条件、面部表情(是否闭眼、是否微笑)和面部细节(是否戴眼镜)等。

(3) AR人脸数据集,含有120组人脸图像,每组包括14副人脸图像,共1680副人脸图,图像的像素是50×40,这些图像之间的区别是不同的光照条件和面部表情(是否微笑、是否大幅张口)等。

图1给出了Extended Yale_B,ORL和AR人脸数据集中的人脸样例。

图1　Extended Yale_B、ORL和AR人脸数据集的图像

3.2　实验设置

实验数据集是在上述标准人脸数据集中构造的,每个数据集被分成3部分:每一组人脸图像先抽取一部分样本(无标签)作为无监督训练数据,再抽取一部分样本(有标签)作为监督训练数据,剩下的样本作为测试数据。

对于基于稀疏重构的3种算法(SPP、SNPP、SSNPP),在进行降维之前先将训练样本的像素值归一化到[0,1]的范围,同时为避免样本数远小于特征维数而导致XXT出现奇异,也为了加快算法运行,将训练样本投影到PCA的子空间进行数据预处理,保留训练样本98%的主成分。

设置各算法的运行参数如表1所示。

表1　各算法的参数

实验按相同的步长递减保留特征的维数,经过降维后的数据,均通过最近邻分类算法计算出识别准确率,以分类的准确率来衡量降维算法的性能。

3.3　结果及分析

3.3.1Extended Yale_B数据集实验

实验中,从Extended Yale_B人脸库随机抽取每组人脸的前40幅图像作为半监督中无标签样本,再抽取10幅图像作为训练样本,剩下的9幅图像作为测试集。参数设置为:NPE算法的近邻样本个数k=3,SNPP算法的近邻样本个数k=20,SSNPP算法的近邻样本个数k=20,融合参数λ=3.5。表2为各算法的最大识别率和平均识别率的比较,图2为不同子空间学习算法的识别准确率与维数的关系曲线。

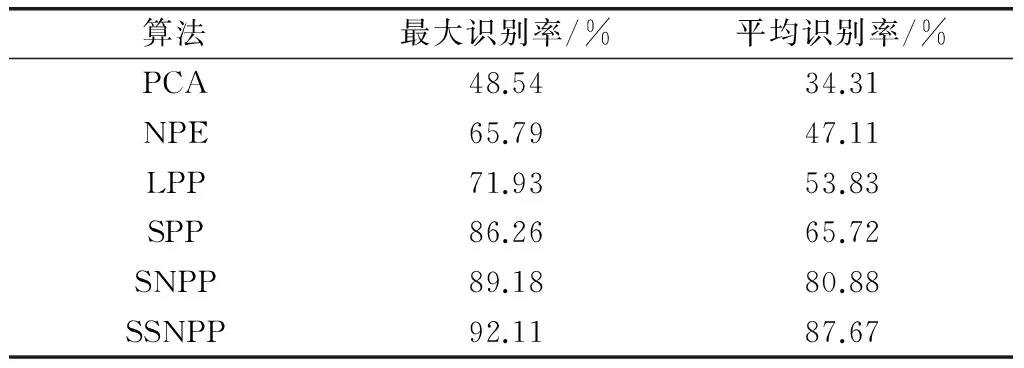
表2　Extended Yale_B人脸库上不同算法的最大识别率和平均识别率

图2　Extended Yale_B人脸库上不同算法的识别准确率

从表2可看出,在最大识别率方面,SSNPP比SPP高5.85%,SNPP比SPP高2.92%;在平均识别率方面,SSNPP比SPP高21.95%,SNPP比SPP高15.16%,这是由于在稀疏近邻相关性重构的时候，利用样本间的局部信息和部分标签信息引入了矩阵Di,使得在稀疏相关性重构样本时,不同类的样本和噪声样本被忽略,保留了更为准确的自然判别信息,提高了降维性能和后续分类的准确率,从而验证了稀疏近邻相关性重构的有效性。

从图2和表2可以看出,SNPP算法的最大识别率为89.18%,比PCA、NPE、LPP、SPP算法中的最高识别率高2.92%,且SNPP算法的整体识别性能均大幅优于这4种算法,这说明稀疏近邻相关性重构充分提取了样本间的局部结构信息和部分样本的标签信息,从而使算法性能得到较大提升。而SNPP算法在65维时识别率达到最高,且随着维数升高,识别率很难再上升,这表明降维后的特征空间能很好地描述原来的特征空间,这说明了稀疏近邻相关性重构在提取判别信息时具有良好的稳定性。

从图2可以看出,SSNPP算法在投影轴维数为55维时识别率达到最大值,最大识别率达到92.11%,比其他5种算法的最高识别率高2.93%。而在全部维度上,SSNPP算法的性能在SNPP的基础上均有提升,这说明SSNPP算法有效地融合了稀疏近邻重构信息和部分样本的标签判别信息,通过判别特征的融合,增强了特征的表示和判别能力,得到了判别能力更强的低维子空间,提高了分类和识别准确性,验证了SSNPP算法的有效性和鲁棒性。

3.3.2ORL数据集实验

实验中,从ORL人脸库中选择每组人脸的前5幅图像作为半监督学习中无标记的训练样本,选择近邻的3副图像作为有标记训练样本,剩下的2幅图像作为测试集。参数设置为:NPE算法的近邻样本个数k=31,SNPP算法的近邻样本个数k=97,SSNPP算法的近邻样本个数k=96,融合参数λ=0.5。表3为各算法最大识别率和平均识别率的比较,图3为在不同子空间学习算法的识别准确率与维数的关系曲线。

表3　ORL人脸库不同算法的最大识别率和平均识别率

图3　ORL人脸库上不同方法的识别准确率

从图3和表3可以看出,SSNPP算法在投影轴维数为55维时识别率达到最大值,最大识别率达到了92.11%,比其他5种算法的最高识别率高2.93%,平均识别率为88.33%也均高于其他5种算法。而在全部维度上,SSNPP算法的性能在SNPP的基础上均有较大提升,这说明SSNPP算法实现了判别信息的有效融合,增强了特征的判别能力,提高了分类和识别准确率,验证了SSNPP算法的有效性和鲁棒性。

3.3.3AR数据集实验

实验中,从AR人脸库中选择每组人脸的前5幅图像作为半监督学习中无标记的训练样本,选择近邻的4幅图像作为有标签训练样本,剩下的5幅图像作为测试样本。参数设置为:NPE算法的近邻样本个数k=160,SNPP算法的近邻样本个数k=77,SSNPP算法的近邻样本个数k=77,融合参数λ=0.365。表4为各算法的最大识别率和平均识别率的比较,图4为不同子空间学习算法的识别准确率与维数的关系曲线。

表4　AR人脸库上不同算法的最大识别率和平均识别率

图4　AR人脸库上不同方法的性能比较

从表4可以看出,在最大识别率方面,SSNPP比SPP算法高4.00%,SNPP比SPP高2.16%;在平均识别率方面,SSNPP比SPP算法高9.71%,SNPP比SPP高6.58%,这也验证了稀疏近邻相关性重构比稀疏相关性重构更为有效。

从图4和表4可以看出,SNPP算法的最大识别率为94.83%,比PCA、NPE、LPP、SPP算法中的最高识别率高2.00%,且SNPP算法的整体识别性能均高于这4种算法,这也说明了稀疏近邻相关性重构能充分利用样本间局部结构信息和部分样本的标签信息,使得算法性能得到较大提升。SNPP算法在60维时识别率达到最高,且随着维数升高,识别率很难再上升,这也验证了稀疏近邻相关性重构在提取判别信息时具有良好的稳定性。

从图4可以看出,SSNPP算法在投影轴维数为60维时识别率达到最大值96.67%,比其他5种算法的最高识别率高2.93%,而在全部维度上,SSNPP的性能均优于SNPP,这同样说明了SSNPP能在标记样本不足的情况下依然能够取得较高的识别率,验证了SSNPP算法的有效性。

4　结　论

本文通过提取样本间的局部结构信息和部分样本的标签信息,对传统稀疏相关性重构方法进行了改进,提出了稀疏近邻相关性重构方法,该方法使得重构保留了更为准确的判别信息,基于此方法得到了SNPP算法。但SNPP算法本质上仍属于无监督学习,不能像MMC算法一样充分利用样本的标签信息。为了进一步提高降维算法的性能,本文利用半监督学习的思想将SNPP算法和MMC算法进行结合,通过引入正则化参数对标签判别信息和稀疏近邻相关性重构信息进行融合,将SNPP算法拓展至SSNPP算法,增强了特征的判别能力。在Extended Yale_B、ORL和AR人脸库上的实验结果表明,SNPP算法的分类和识别性能与传统降维算法相比取得大幅提升,这验证了稀疏相关性重构的有效性和提取判别信息时具有的良好稳定性;而SSNPP算法的性能在3个人脸库上与SNPP算法相比均有较大提升,这说明SSNPP算法具有很好的鲁棒性,但对于稀疏表示误差较大的样本,和一些非线性分布比较复杂的数据,本文算法还是难以处理,这也是今后值得研究的方向。

参考文献：

[1] JOLLIFFE I. Principal component analysis[M]. New York: Wiley, 2002.

[2] MIKA S, RATSCH G, WESTON J, et al. Fisher discriminant analysis with kernels[C]∥Proc.of the IEEE Signal Processing Society Workshop, 1999: 41-48.

[3] HE X, NIYOGI P. Locality preserving projections[C]∥Proc.of the Advances in Neural Information Processing Systems, 2004: 153-160.

[4] HE X, CAI D, YAN S, et al. Neighborhood preserving embedding[C]∥Proc.of the 10th IEEE International Conference on Computer Vision, 2005: 1208-1213.

[5] QIAO L, CHEN S, TAN X. Sparsity preserving projections with applications to face recognition[J]. Pattern Recognition, 2010, 43(1): 331-341.

[6] 马小虎,谭延琪. 基于鉴别稀疏保持嵌入的人脸识别算法[J]. 自动化学报, 2014, 40(1): 73-82.

MA X H, TAN Y Q. Face recognition based on discriminant sparsity preserving embedding[J]. Acta Automatica Sinica, 2014, 40(1): 73-82.

[7] WRIGHT J, YANG A Y, GANESH A, et al. Robust face recognition via sparse representation[J]. IEEE Trans.on Pattern Analysis and Machine Intelligence, 2009, 31(2): 210-227.

[8] HUI K, LI C, ZHANG L. Sparse neighbor representation for classification[J]. Pattern Recognition Letters, 2012, 33(5): 661-669.

[9] ELHAMIFAR E, VIDAL R. Robust classification using structured sparse representation[C]∥Proc.of the IEEE Conference on Computer Vision and Pattern Recognition,2011:1873-1879.

[10] ZHANG D, ZHOU Z H, CHEN S. Semi-supervised dimensionality reduction[C]∥Proc.of the International Conference on Data Mining of the Society for Industrial and Applied Mathematics, 2007: 629-634.

[11] CAI D, HE X, HAN J. Semi-supervised discriminant analysis[C]∥Proc.of the 11th IEEE International Conference on Computer Vision, 2007: 1-7.

[12] GAO Q, HUANG Y, GAO X, et al. A novel semi-supervised learning for face recognition[J]. Neurocomputing,2015,152(C): 69-76.

[13] 刘建伟, 刘媛, 罗雄麟. 半监督学习方法[J].计算机学报, 2015, 38(8): 1592-1617.

LIU J W, LIU Y, LUO X L. Semi-supervised learning methods[J].Chinese Journal of Computers,2015,38(8):1592-1617.

[14] ZHANG X, HU Y N, Zhou N, et al. Semi-supervised sparse dimensionality reduction for hyperspectral image classification[C]∥Proc.of the IEEE Region 10 Conference, 2016: 2830-2833.

[15] WANG X, GAO Y, CHENG Y. A non-negative sparse semi-supervised dimensionality reduction algorithm for hyperspectral data[J]. Neurocomputing, 2016, 188: 275-283.

[16] SHEIKHPOUR R, SARRAM M A, GHARAGHANI S, et al. A survey on semi-supervised feature selection methods[J]. Pattern Recognition, 2017, 64(C): 141-158.

[17] DONOHO D L. Compressed sensing[J]. IEEE Trans.on Information Theory, 2006, 52(4): 1289-1306.