耦合对半实物射频仿真的影响分析

唐 波，盛新庆，金从军，赵小阳

（1．北京科技大学计算机与通信工程学院，北京100083；2．北京理工大学信息与电子学院电磁仿真中心，北京100081；3．北京仿真中心，北京100037；4．中国人民解放军96610部队，北京100085）

唐 波1，盛新庆2，金从军3，赵小阳4

（1．北京科技大学计算机与通信工程学院，北京100083；2．北京理工大学信息与电子学院电磁仿真中心，北京100081；3．北京仿真中心，北京100037；4．中国人民解放军96610部队，北京100085）

网络优先出版地址：http：／／kns．cnki．net／kcms／detail／11．2422．TN．20180103．0946．002．html

三元组射频仿真是电子系统进行外场试验前的必要步骤，仿真的有效性取决于电子系统在室内仿真与外场试验下的响应一致性。研究了耦合效应对三元组射频仿真的影响。通过理论分析与全波电磁计算，分析了发射端三元组单元间的耦合、接收端单元间耦合对仿真的影响。结果表明，当接收端方向图在三元组邻域内均匀时，发射端的单元间耦合可以忽略；当接收端各支路的天线之间耦合参数与电磁波照射方向无关时，接收端耦合对射频仿真无影响。基于文中参数，发射端耦合、接收端耦合造成的仿真误差分别低于总仿真误差两个数量级、一个数量级。

三元组；射频仿真系统；耦合；仿真精度

网址：www．sys－ele．com

0 引 言

在导弹系统的研发过程中，进行外场试验是很必要的，需要花费大量的试验费用。为了提高试验成功率和效费比，在进行外场试验之前要开展室内的仿真实验。世界上一些主要国家，现在都建有半实物射频仿真实验室，例如，美国、英国、俄罗斯等，我国航天部门的一些研究院所也设有此类实验室［1－2］。半实物射频仿真通过在微波暗室环境下，模拟真实的外场环境，使待测导弹等电子设备可以获得与外场真实环境下相同的测试数据。

文献［3］首先提出三元组的射频仿真结构，基于此进行室内的射频仿真实验，其原理是基于角闪烁［4］。通过使用3个辐射单元，可以生成一个空间中的散射点目标。根据角闪烁方程，散射点的方位取决于三元组的3个辐射单元的馈电电压相对幅度相位关系。通过调整三元组各单元的馈电电压，可以实现对所模拟的点目标的控制，从而可以仿真出点目标在空间中的运动轨迹，实现导弹等电子系统的仿真环境。

文献［5－11］对三元组射频仿真的研究，主要集中于误差分析，以及近场效应、近场修正等方面。三元组的点目标方向仿真误差主要来源于电参数误差、位置误差、模型误差等［12－13］。电参数误差包括三元组馈电系统的幅相误差、单元的等效相位中心误差等；位置误差包括转台位置误差等；模型误差指的是所用计算点目标方向的模型存在误差，例如使用重心公式计算目标方位，就会带来近场误差［14－15］。近场效应是指在近场条件下，使用重心公式将会带来较大误差的效应［11］。由于重心公式是从远场条件导出的，其非常简单，易于计算，因此仍然被广泛使用，只是要辅之以近场误差修正表［16－17］。近场修正通常可以有两种途径，一是通过实验，二是通过严格的全波电磁数值计算。近场修正中，需要从给定的点目标方向反推出三元组各单元的馈电电压，这是一个逆过程。因此，近场修正中需要不停地进行迭代，直到收敛。迭代的方法包括根据接收机响应计算出角度关于馈电电压的梯度，以及使用优化算法等。近来对于三元组射频仿真的研究比较集中于仿真精度的提高、多点目标的仿真等［18－19］。为了进一步提高三元组的仿真角度精度，文献［20］给出了使用多元组进行仿真的方法，通过优化多元组的馈电电压，获得比传统三元组更高的射频仿真精度。文献［21］提出通过分集技术来提高仿真精度。

本文主要分析耦合对射频仿真的影响。虽然在近场修正中，实验法和全波法都包含了耦合效应在内，然而耦合的影响程度以及如何影响未见公开报道。由于仿真系统仿真精度进一步提高面临着瓶颈，分析影响仿真精度的每一项因素显得非常必要。耦合是其中一项因素。因此，分析耦合对仿真的影响对于进一步提高仿真精度是必要的。

本文所指的室内仿真实验是指在微波暗室中，使用三元组照射真实的待测导弹，测试导弹的相关性能。由于导弹是真实的，目标的回波是使用三元组的辐射波合成模拟的，因此属于半实物射频仿真。仿真是在暗室环境下，通过三元组辐射向导弹的射频前端输入与真实环境下相同的角度信息。仿真误差是指输入角度信息的偏差。

1 三元组原理

一般认为，三元组基于角闪烁原理［3－4］。从室内仿真与外场试验一致性的角度来考察三元组仿真的原理。

将坐标（R，θ，φ）转化为坐标（R，x，y）。其中

表达了目标的方向信息。假设目标点P0的方位为（x0，y0），三元组的3个单元Pi的方位为（xi，yi），i＝1，2，3。

令待测电子系统射频接收前端的某个接收点的空间回波方位响应函数为p（x，y），其为复函数，可以是干涉仪的一路接收信号，也可以是比幅式单脉冲雷达的一路接收信号。注意：p（x，y）是比幅比相处理前的数据。将p（x，y）在（x0，y0）邻域内进行泰勒级数展开，得

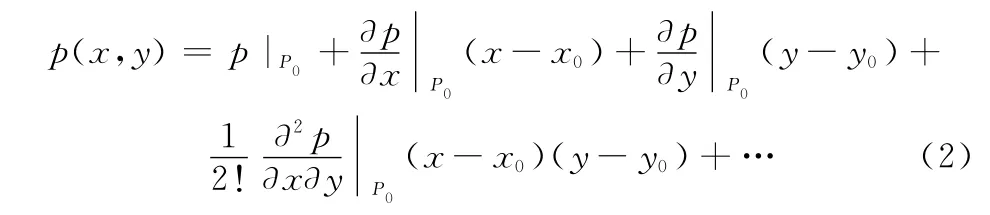
仿真的目的是要在微波暗室环境中及在外场试验条件下，在待测电子系统的各接收通路中产生相同的关于空间方位的响应，即有仿真等效性方程为

略去高阶项，可得

式中，Δp为对p的梯度运算，p为复数时，分别对实部和虚部求梯度。进一步得

因而

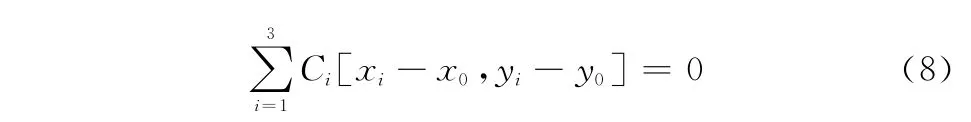
由式（4）和式（8）得幅度重心公式为

式（8）的导出与p的具体形式无关，那么，式（9）满足任意未知待测响应函数的要求。此外，那些略去的高阶项将引起近场效应，产生近场误差。

2 发射端耦合效应

发射端的耦合即辐射单元之间的耦合，在此考虑其对仿真精度的影响。实际工作中，三元组不是孤立存在的，而是处于整个辐射阵列中，单个辐射单元同样处于整个辐射阵列中。由于阵元周期性地规律排列，除去阵列边缘的辐射单元，绝大部分辐射单元间的自阻抗和互阻抗是相同的。对于三元组的3个单元来说，耦合对幅度的影响具有一致性，因此，耦合效应不会通过影响幅度对仿真角度误差产生影响。

距离位置影响初相位的计算，对于三元组的3个单元，该相位误差具有一致性，因而只考虑角位置的影响。耦合对辐射单元位置的影响如图1所示。

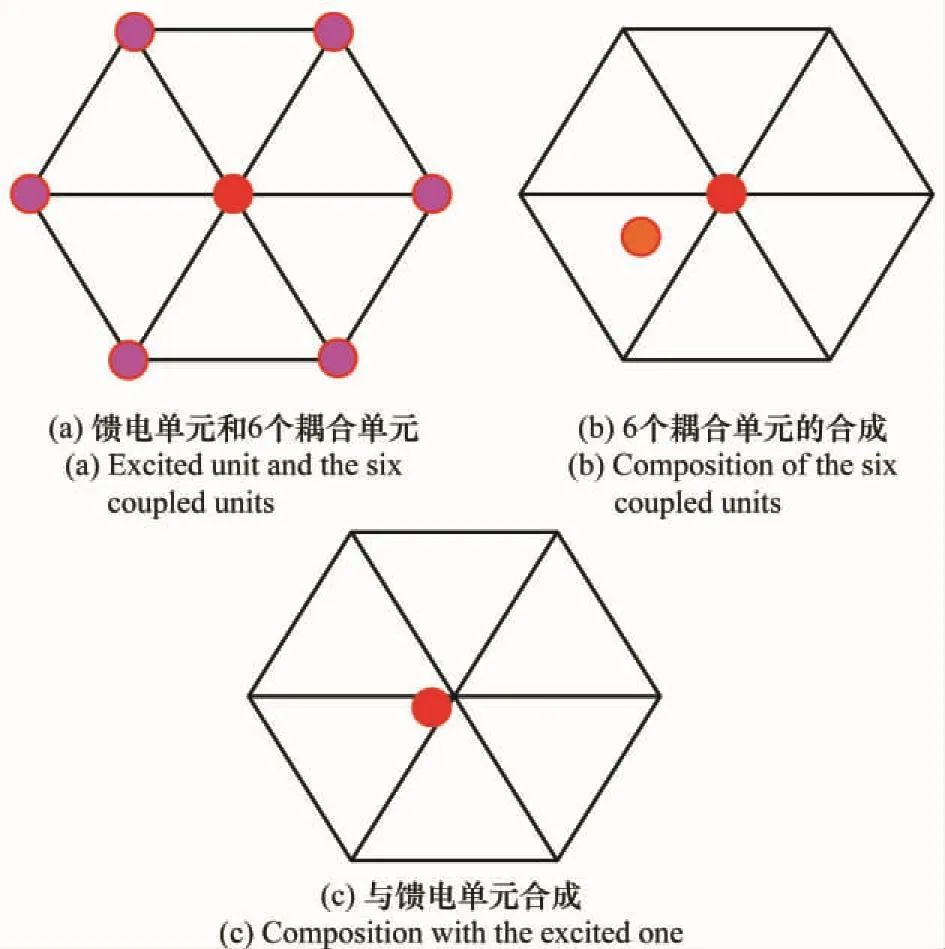
图1 耦合处理示意图Fig．1 Sketch map of processing for coupling

由图1可知，当仅有第i个单元（红色）馈电且其幅度为Ci时，其周围耦合效应最强的6个辐射单元（浅红色）耦合出的幅度各为ρCi，ρ为耦合参数。这6个单元将合成一个虚拟单元，如图1（b）所示。该虚拟单元将与第i个单元合成，从而拉偏第i个单元的位置，如图1（c）所示。假设接收端的天线单元方向图是全向的，若采用平行线近似（即待测电子系统处于无穷远），则该6个耦合单元的合成点目标位置就在第i个辐射单元处，不产生位置误差。实际上，微波暗室的长度有限，待测系统位于有限距离处，存在近场效应。此时近场误差由平行线近似的高阶小量决定。而距离的平行线近似高阶小量的量级为l4／R3，其中l为三元组边长。对应耦合单元合成点的角度误差量级为

式中，k为波数。对于绝大部分射频仿真系统，式（10）数值结果都是极微小的量。例如，对于波长为0．1m，三元组张角30mrad，式（10）数值结果为4．3×10－7rad。这是6个耦合单元的合成虚拟点目标的位置偏移量，考虑到这些耦合单元的电流应远小于第i个辐射单元的电流，其对第i个辐射单元的位置拉偏作用还应远小于式（10）的表达。因此，若不考虑接收端天线单元的方向图，发射端耦合可以不予考虑。

式（10）是假设接收天线方向图为全向或足够平坦而得出的。若接收端天线方向图不够平坦，则耦合的6个单元将不再是等幅叠加，这将造成6个单元的虚拟合成点产生较大的位置偏移。假设接收天线单元的场方向图在其中一维上用典型的sinc函数表示为sinc（πθ／θw），θw为接收天线单元的零点波束宽度。当接收天线单元方向图最大值指向其中一个耦合单元时，在远端的耦合单元幅度最小，此时可以估算出6个耦合单元的相对幅度偏差量级为

幅度的偏差效应可以看成是在原位置处放置了一个幅度等于该幅度偏差的辐射点，而把原来6个等幅点略去。将此偏差看成是在原来6个耦合点被均匀照射的基础上额外增加的辐射点相对于原耦合点的幅度。因而，该额外增加的辐射点相对于被馈电的第i个单元的相对幅度量级应为

由重心公式可知，由发射端耦合效应所造成的被馈电第i个单元的等效辐射中心的偏移量级为

通过优化阵列布置，可使该偏移远小于仿真角度误差要求。式（13）中，ρ和l是一对矛盾，较小的l会产生较大的ρ，反之亦然。因此在设计仿真系统时需要进行折衷处理，以获得最优值。

前述分析考虑了最强的6个耦合点。更远的耦合点由于ρ随距离的衰减速度远大于线性衰减，根据重心公式可知偏移效应随距离仅呈线性增长，因此远处耦合单元的偏移效应远小于最近的6个耦合单元。所以，仅需考虑该6个耦合单元即可。

3 接收端耦合效应

在接收端不同通路之间存在耦合效应。例如，干涉仪的几个接收支路接收天线之间会存在耦合作用，比幅式单脉冲雷达的几副天线之间也会存在耦合作用。下面针对比幅和比相两种情况讨论耦合对仿真的影响。为了表达简洁又不失一般性，分析以基线沿某个方向的两个接收支路的情况为例。另一维上应有相同的分析结果。

无耦合时，假设两个接收支路在馈电接收点处空间回波的方位响应函数分别为p（x，y）、q（x，y），如图2所示。

图2 接收支路耦合示意图Fig．2 Sketch map of receiving structure

对于比相式测角，需要通过两个支路的相位比较来确定目标位置。仿真比相输出应该与点目标回波比相输出相同。

对于比幅式测角，是通过幅度比值的测量来获取角度信息。无论是比相还是比幅，只要在图2中两个馈电点处接收到的仿真信号与外场试验信号相同，都会给出相同的处理结果。因此，在不考虑耦合的情况下，仿真的等效性方程为

只要式（14）成立，不论后端处理方式是比相还是比幅，仿真实验和外场试验都会给出相同的测角输出。当馈电系数Ci使式（14）成立时，其能否使耦合情况下的等效性方程为

仍然成立。若不成立，将产生怎样的仿真角度误差，即为耦合效应所引起的仿真误差。

表1 各点在支路中的响应Table 1 Response of the points

根据式（14），F1、F2与T1、T2分别对应。F3通过与F1合成，拉偏F1，使其偏离T1。由于（ρ（xi，yi）－ρ（x0，y0））一般具有很小的量值，可看成是对Ci的微扰，将使F1角度偏移。以对称镜面为零点位置，F3的x位置为

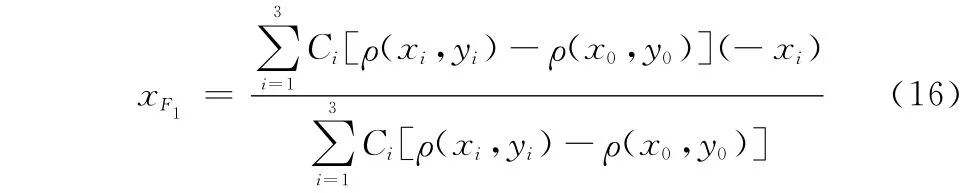
式中，xi前的负号表示三元组单元的镜像位置。与F1点合成后的位置为

对F1点的偏移量为

将式（16）、式（17）代入式（18），得

由式（19）可知，耦合引起的仿真误差与耦合参数的变化率有关，变化越快误差越大；耦合引起的仿真误差还与三元组相对于接收口面的轴向偏移有关，偏移越大，仿真误差越大。注意式（19）的导出是基于针对F1、F3的重心公式，因此其精度受重心公式使用条件的限制。当导引头严重偏离目标或耦合误差远小于重心公式误差时，该式精度较差。考虑到耦合参数可取复值，在三元组角度内耦合参数的相位变化很小，此时可对式（19）计算结果取模。

将式（1）代入式（19），假设φ不变，考察θ的误差，得

若ρ与入射波方向（x，y）无关，由式（19）、式（20）可知仿真误差为零。事实上，当ρ为常数时，可由式（14）导出式（15）。只要馈电系数Ci使非耦合情况下的等效性方程成立，那么耦合情况下的等效性方程仍然成立。此时耦合对于仿真的等效性没有影响。因为耦合不仅会对微波暗室环境中三元组的辐射波有影响，也会对外场试验中的目标回波信号有影响，若ρ与入射波方向（x，y）无关，则这两种影响是相同的。

测角误差与仿真误差是两个不同的概念，前者是待测系统的输出结果角度与真实来波角度的差值，后者是暗室中输出结果角度与外场中输出结果角度之差、或暗室中的测角误差与外场中的测角误差之差。

4 数值算例

考虑到计算精度和复杂性，以半波振子作为干涉仪接收支路的天线。振子的排列方式与入射电磁波的相对位置关系如图3所示。

图3 半波振子接收示意图Fig．3 Sketch map of half－wavelength dipoles receiving

由图3可知，入射面为YZ平面，基线沿Y轴，基线长度为两个波长。图3（a）为垂直极化波，电场沿X方向，天线沿X取向；图3（b）为平行极化波，电场在YZ面内，天线沿Z取向。波长0．1m，暗室距离20m。为了仿真YZ平面内某个方向入射的电磁波，在YZ平面内设置两个辐射单元构成二元组，张角为2°。其中一个辐射单元处于θ＋1°，另一个处于θ－1°处。两个单元的馈电系数Ci可以根据式（14）得到，分别为

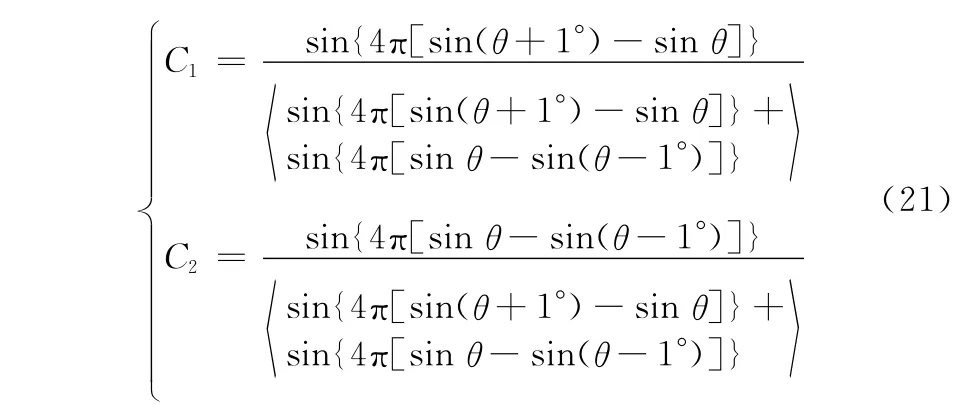
垂直极化情况下的外场试验测角误差与室内仿真实验测角误差曲线如图4所示。

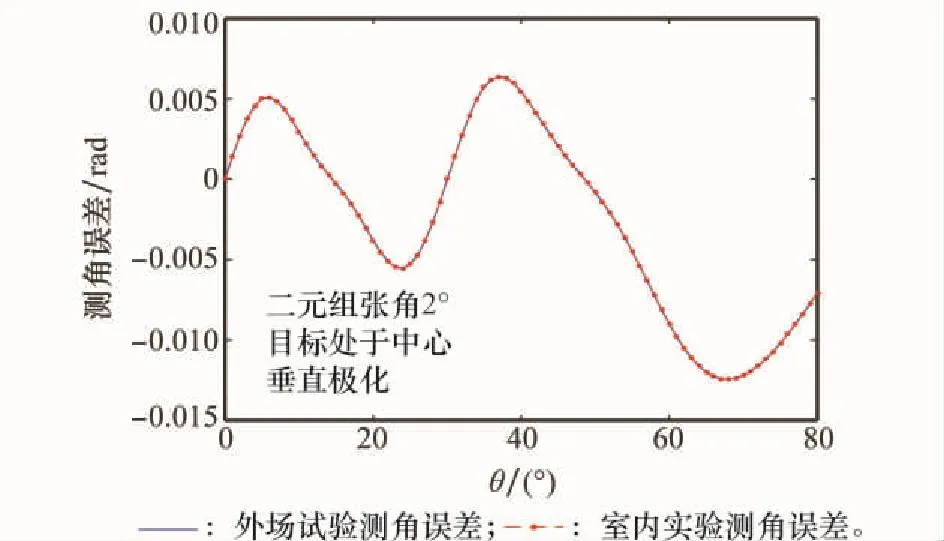
图4 测角误差随θ的变化（垂直极化）Fig．4 Measured angle error V．S．θ（Perpendicular polarization）

由图4可知，由于耦合的存在，干涉仪的测量值与真实来波方向之差可以达到数个mrad。因此，从系统标定的角度来看，耦合是需要考虑的。然而，从射频仿真等效性的角度来看，这两条测角误差曲线非常接近，近乎重合。这两种测角误差之差，即为仿真误差，其随θ的变化情况如图5所示。

图5 仿真误差随θ的变化（垂直极化）Fig．5 Simulation error V．S．θ（Perpendicular polarization）

由图5可知，仿真误差应为零。这是由于对于垂直极化的情况，不论入射角度θ为何值，振子上的入射场皆相位一致、幅度均匀，因而耦合参数ρ恒定不变，从而使仿真误差为零。

平行极化情况下的外场试验测角误差与室内仿真实验测角误差曲线如图6所示。

图6 测角误差随θ的变化（平行极化）Fig．6 Measured angle error V．S．θ（Parallel polarization）

由图6可知，由于耦合的存在，干涉仪的测量值与真实来波方向之差可以达到数个mrad。这与垂直极化的图4基本相同。因此，从系统标定的角度来看，平行极化的耦合也是需要考虑的。然而，从射频仿真等效性的角度来看，这两条测角误差曲线非常接近，近乎重合。仿真误差如图7所示。

图7 仿真误差随θ的变化（平行极化）Fig．7 Simulation error V．S．θ（Parallel polarization）

由图7可知，仿真误差不为零，达到了10－5rad量级。这是由于耦合参数ρ不再恒定不变，从而使仿真误差不为零。当入射角为零时，仿真误差为零，然后逐渐增大，在40°附近逐渐减小；当入射角减为90°时，是垂直极化，因此仿真误差为零。平行极化条件下，耦合参数｜ρ｜随θ的变化如图8所示。

图8 耦合参数｜ρ｜随θ的变化（平行极化）Fig．8 Coupling parameter｜ρ｜V．S．θ（Parallel polarization）

由图8可知，耦合参数随着入射角增大而逐渐增大。

然后对发射端耦合的情况进行全波法电磁计算。作为发射端的三元组一般采用喇叭天线，因此对由3个喇叭组成的位于阵列边缘的三元组的情况进行数值计算。

辐射三元组如图9所示，采用矩形喇叭，喇叭口径为a＝0．044m，b＝0．057 4m；喇叭间距d＝0．648m。工作频率为15GHz，三元组与转台的距离为18m。采用多层快速多极子加速的全波法计算，对3个喇叭进行整体电磁建模。

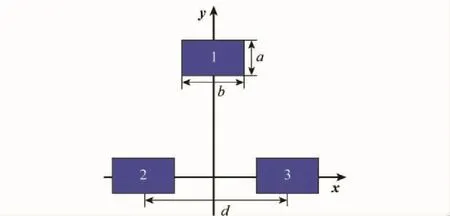
图9 辐射三元组Fig．9 Transmitting TUA

由图9可知，令单元1进行馈电，而其他两个单元不馈电。若不存在耦合，转台处的电磁波能流方向是单元1的视线方向。由于存在耦合，通过整体建模计算，得到转台处的电磁波能流方向，偏离单元1的视线方向，该偏离值为0．002mrad。考虑到这是阵列边缘的三元组，若为阵列内部的三元组，该偏离值应该更小。

5 结 论

仿真角度误差即仿真误差反映了室内射频仿真对室外试验的等效程度。发射端的耦合、接收端的耦合都有可能影响仿真误差。对于发射端的耦合，当接收端的接收方向图在三元组邻域内平坦、均匀时，一般可以忽略；当接收端的接收方向图在三元组邻域内非均匀时，有可能产生显著的耦合，需要根据实际参数进行细致的考虑分析。对于接收端的耦合，当各接收支路的天线之间耦合参数与电磁波照射方向无关时，耦合对射频仿真的影响为零；当各接收支路的天线之间耦合参数与电磁波照射方向有关时，耦合对射频仿真的影响一般不为零。耦合参数的变化越剧烈，接收机越偏离目标点，接收端耦合对射频仿真的误差影响越大。

［1］李金顺，刘金．美国埃格林空军基地半实物仿真试验20年［J］．飞航导弹，1999，29（4）：41－45．LI J S，LIU J．HWIL in US Eglin AFB for 20years［J］．Winged Missiles Journal，1999，29（4）：41－45．

［2］刘天舒，金从军．近场效应修正算法有效性验证方法［C］∥第三届中国导航、制导与控制学术会议论文集，2010：99－103．LIU T S，JIN C J．Verifying method of near field error compensation of RFSS［C］∥Proc．of the 3rd China Guidance Navigation and Control Conference，2010：99－103．

［3］POLKINGHORNE A A．Radio frequency simulation system （RFSS）system design handbook［R］．Boeing Company D243－10004－1，1975．

［4］HOWARD D D．Radar target angular scintillation in tracking and guidance systems based on echo signal phase front distortion［C］∥Proc．of the National Electronics Conference，1959：840－849．

［5］BISHOP C B．Error analysis of point targets in HWIL simulation［C］∥Proc．of the 16th Century Society and Conference，1994：373－378．

［6］王海涛，朱根才，贲德，等．射频仿真系统的误差分析与可信度评估研究［J］．系统仿真学报，2007，19（7）：1548－1550．WANG H T，ZHU G C，BEN D，et al．Study on error analysis and reliability estimate for RFSS［J］．Journal of System Simulation，2007，19（7）：1548－1550．

［7］肖卫国，尔联洁．雷达制导半实物仿真误差分析［J］．系统仿真学报，2007，19（11）：2461－2463 XIAO W G，ER L J．Error analysis of radar guidance hardwarein－the－loop simulation［J］．Journal of System Simulation，2007，19（11）：2461－2463．

［8］王泗宏，黄惠明，李军，等．射频仿真幅相控制误差对目标位置精度的影响分析［J］．飞行器测控学报，2007，26（2）：59－63．WANG S H，HUANG H M，LI J，et al．Analysis of the influence of amplitude and phase errors on target position precision in RFSS［J］．Journal of Spacecraft TT ＆C Technology，2007，26（2）：59－63．

［9］MCPHERSON D A．Near field angle error compensation for high precision HWIL RF missile seeker simulation［C］∥Proc．of the 16th Century Society and Conference，1993：640－645．

［10］李宗彬，杨刚，陈潜，等．引信半实物射频仿真中的近场效应［J］．上海航天，2009，26（4）：92－95．LI Z B，YANG G，CHEN Q，et al．The short range effect in fuze RF simulation［J］．Aerospace Shanghai，2009，26（4）：92－95．

［11］陈训达．射频仿真中的双近场效应［J］．系统仿真学报，2001，13（1）：92－95．CHEN X D．The dual near field effect in radio frequency simulation［J］．Journal of System Simulation，2001，13（1）：92－95．

［12］俞梦霞，李曦，吕飞．关于射频目标跟踪半实物仿真系统设计［J］．计算机仿真，2016，33（5）：100－104．YU M X，LI X，L F．Design of hardware－in－loop simulation system for radio frequency target tracking［J］．Computer Simulation，2016，33（5）：100－104．

［13］武鹏飞，何秋茹．幅相控制精度对射频仿真目标位置误差的影响［J］．现代防御技术，2016，44（6）：167－173．WU P F，HE Q R．Influence of amplitude and phase precision for target position error in RF［J］．Modern Defense Technology，2016，44（6）：167－173．

［14］XIAO S，MIGLLIACCIO M，CAMP J T，et al．Focusing pulsed electromagnetic radiation in the near field［C］∥Proc．of the IEEE Pulsed Power Conference，2009：495－498．

［15］LU J，SHEN Y，NI H．Near field effect on the location precision of RFSS［C］∥Proc．of the International Conference on Computational Electromagnetics and its Applications，1999：547－548．

［16］付璐．复合阵列射频仿真系统的近场效应修正［D］．上海：华东师范大学，2016．FU L．Near field effect correction on composite array radio frequency simulation system［D］．Shanghai：East China Normal University，2016．

［17］徐自玲．三元组射频仿真误差修正设计与实现［D］．成都：电子科技大学，2015．XU Z L．The design and realization of radio frequency simulation error correction in a ternary array［D］．Chengdu：University of Electronic Science and Technology of China，2015．

［18］TANG B，SHENG X，JIN C，et al．Angle error analysis of multiple－target HWIL RFSS［C］∥Proc．of the Target and Environment Modeling and Simulation Technology Conference in China，2015：145－154．

［19］何骁，章锦文，田建伟．射频仿真多辐射中心方案设计及幅相误差分析［J］．计算机仿真，2010，27（4）：111－116．HE X，ZHANG J W，TIAN J W．Project design for RFSS of multi－radiation centers and its amplitude and phase error analysis［J］．Computer Simulation，2010，27（4）：111－116．

［20］唐波，盛新庆，金从军，等．基于多元组提高射频仿真角度精度的方法［J］．系统工程与电子技术，2016，38（10）：2435－2440．TANG B，SHENG X Q，JIN C J，et al．Method of improving the angle accuracy of the RFSS based on multiple－radiating－unit array［J］．Systems Engineering and Electronics，2016，38（10）：2435－2440．

［21］唐波，盛新庆，金从军，等．基于分集技术的射频仿真角度精度提高［J］．系统工程与电子技术，2017，39（9）：2143－2148．TANG B，SHENG X Q，JIN C J，et al．Improvement of the angle simulation accuracy of the RFSS based on diversity［J］．Systems Engineering and Electronics，2017，39（9）：2143－2148．