不完全共因失效系统可靠性预测贝叶斯更新

蒋子涵, 方志耕, 芮菡萏, 张习习, 刘思峰

(南京航空航天大学经济与管理学院, 江苏 南京 211106)

0　引　言

共因失效(common cause failures, CCF)是一种相依失效,表现为在同一原因下,系统内的多个元件同时或在很短的时间间隔内相继发生失效。CCF是冗余设计的天敌,其会大大增加元件发生关联失效的概率,严重降低系统的可靠性。此外,在航空工业、电子工业及核电工业等领域里,CCF是导致系统失效的重要原因,忽略共因的影响将会使可靠性分析产生较大误差。因此,学者们投入了大量精力来研究CCF的概率分布形式,及其可能对各元件产生的影响。

从1970年代开始,学者们就提出了许多用于分析CCF的模型,包括β因子模型、α因子模型、多希腊字母模型等,在此基础上也进行了很多研究工作[1-4]。进入21世纪后,随着系统结构的复杂化以及更多研究案例的出现,对CCF的研究进入了新阶段。文献[5]在传统模型的基础上提出作用矩阵的概念,指出共因是以一定概率给每个部件造成不同程度的影响,从而增加了马尔可夫过程的适用性;类似地,文献[6]研究了多阶段任务系统的概率共因故障问题,提出了分析系统可靠性的显式和隐式方法;文献[7]也考虑了概率共因故障模型,并结合随机方法和动态故障树来研究带有备件门的冗余系统可靠性。文献[8-9]结合了蒙特卡罗模拟和元胞自动机两种算法,在传统方法只能分析可以转化为串、并联结构的简单系统的基础上,进一步评估了复杂系统的可靠性。文献[10]利用有序二叉决策图,建立了具有时延约束的网络可靠性模型,从CCF角度分析了航空电子系统的网络可靠性。而文献[11]则以有序二叉决策图为工具研究带有非独立传播效应的共因故障系统的可靠性。

核电行业作为CCF的重要应用领域,也产生了很多研究成果。文献[12-13]以核电站为研究背景,构建了一种包含扩散和选择性失效的多状态系统模型,并提出广义发生函数来计算可靠度。文献[14]运用蒙特卡罗仿真研究了发生自然灾害(如地震)时核电站的概率安全评价问题。

近年来,学者们的研究对象逐渐从单一状态系统转变为多状态系统,同时一些新的技术也被用来求解更复杂的系统,常见的方法包括目标导向的流图法(goal oriented-FLOW,GO-FLOW),马尔可夫链和贝叶斯网络。其中文献[15]用统一的映射规则把离散时间贝叶斯网络和GO-FLOW结合起来,使带有复杂特征的GO-FLOW模型能被转化为离散时间贝叶斯网络模型。文献[16-17]基于马尔可夫过程,分别结合多状态分析和故障反应分析,提出了冗余分配的方法。最后,贝叶斯网络也是学者们研究的重点。文献[18-19]均建立了系统的动态贝叶斯网络模型,以便发现多种故障冲击下系统的薄弱环节;文献[20]则以物联网为研究对象,设计了贝叶斯网络中新的节点连接方式,分析了物联网的全端可靠性。

本文考虑不完全CCF机制,认为共因只以一定概率p(发生共因时,单一元件的失效概率)使相关元件发生失效,使得可靠性预测模型更符合现实。目前对不完全CCF的研究只是通过失效次数和总试验时间来估计多重失效率,本文进一步利用失效时刻数据来进行多重失效率的贝叶斯更新,不仅使估计结果更准确,也能利用新信息来动态预测系统的可靠性。此外,在已有研究仅考虑CCF率的基础上,本文还考虑了元件的独立失效率,并通过贝叶斯方法对独立失效率的估计值进行更新,使得模型同时包含了独立失效和不完全CCF的特征。

本文希望通过该模型更准确地预测系统可靠性,并通过计算可靠度分位点寿命来合理确定系统的检修周期,使系统可靠性维持在一个较高水平。

1　不完全CCF系统可靠性模型

1.1　共因的发生率

共因分为系统外部冲击和内部故障。假定共因的到来是一个泊松过程,则相邻两次共因发生的时间间隔Δt服从指数分布,记为Δt～Exp(μ)。

若系统中共有m个元件,且都属于同一个失效分布,称为相同分布单元。令λi表示发生共因时,系统中指定i个元件同时失效的失效率;λiVm表示发生共因时,系统中任意i个元件同时失效的失效率,则有

λi=μpi(1-p)m-i

(1)

(2)

(3)

(4)

式中,Cq(p)表示发生q重以上失效的概率,即

(5)

假如共因到来时,每个元件发生失效的概率p各不相同,那么λi和λiVm的表达式就会因元件组合不同而变化。例如假设系统中有3个元件,在共因下发生故障的概率分别是p1,p2和p3,这时可设λ1,2为1、2号元件同时失效的失效率,即λ1,2=p1p2(1-p3),其他情况以此类推。

推论1设{N1(t),t≥0}和{N2(t),t≥0}为两个独立的泊松过程,且强度分别为λ1和λ2,则这两个泊松过程的叠加{N(t),t≥0}是一个强度为λ=λ1+λ2的泊松过程。

不难证明,推论1可以推广到有限个独立泊松过程相叠加的情形，如图1所示。

图1　独立泊松过程的叠加

(6)

(7)

(8)

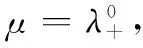
为了计算共因下元件失效概率p的最大似然估计值,可根据观察时间T内的一组统计数据N2Vm,N3Vm,…,NmVm来构造p的最大似然函数,即

L(p)=P(N2Vm,N3Vm,…,NmVm)=

(9)

式中,q=(1-p)。可见L(p)的核是式(9)的后半部分,即

(10)

通过对式(10)求导,即可解出p的最大似然估计值p*。

1.2　元件的状态描述方法

假设系统由m个元件组成。为了对元件的正常或故障状态进行表示,引入以下符号来表示正常或故障事件[21]:

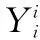
(11)

1.3　系统可靠性分析方法

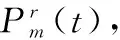
P(x1)P(x2|x1)P(x3|x1x2)…

P(xr|x1x2x3…xr-1)

(12)

(13)

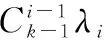
2　系统可靠性参数的贝叶斯更新

2.1　共因发生率μ的贝叶斯更新

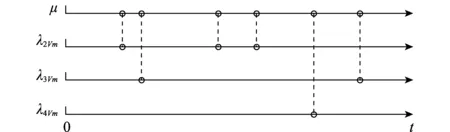
图2　共因发生与多重失效

共因以μ的发生率到达,在该段时间内共发生6次共因。每次发生共因时,系统相应出现了二重、三重和四重失效,且失效率分别为λ2Vm,λ3Vm和λ4Vm。因此多重失效率之和反映了共因的发生率μ。由式(4)和推论1可知,这样的做法是可行的。具体的步骤如下:

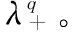
与独立失效率的分析不同的是,CCF分析应将系统作为一个整体来研究,因此把每一次CCF看作一个样本点。由于已知共因的发生是一个泊松过程,因此系统在共因作用下的寿命服从指数分布族,那么样本的似然函数为

(14)

(15)

(16)

(17)

2.2　元件独立故障率λ的贝叶斯更新

设元件在无共因作用时的寿命T服从指数分布Exp(λ),即元件的独立失效率为λ,则寿命的分布函数是F(t)=1-e-λt。对λ进行贝叶斯估计的步骤如下:

步骤1由于有过往寿命试验的统计数据,故假设λ的先验分布为Gamma分布,即π(λ)～Ga(a,b),先验概率密度函数为

(18)

步骤2现对m个该种元件进行了新的寿命试验,假设共测得r次失效,且各失效时刻为t1≤t2≤…≤tr≤τ(r≤m),其中τ为指定的观察中止时间。该样本的似然函数为

(19)

步骤3依据先验信息和新试验数据,并由连续变量的贝叶斯公式可得λ的后验概率密度为

(20)

将式(18)和式(19)代入式(20),可得

(21)

步骤4式(21)中等号右端是Gamma分布的一个核,即π(λ|t1,t2,…,tr)∝λa+r-1e-(b+Tr)λ。因此λ的后验分布服从Gamma分布,即π(λ|t1,t2,…,tr)～Ga(a+r-1,b+Tr),因此可得λ的贝叶斯估计值为

(22)

3　实例分析

某民航客机上搭载的飞行数据记录系统由8个元件组成,其结构如图3所示。其中1、2号元件是缓降系统的一部分,由同一个电路控制,若出现电压异常,可能会导致元件失效,因此其组成CCF组1;此外,1、2号元件各自会因为相应的传感器或电机故障而发生独立失效。5、7、8号元件是数据传输系统的一部分,由另一个电路控制,电压异常同样会导致元件失效,因此其组成CCF组2。同一个CCF组内的元件为相同分布单元。而3、4、6号元件只发生独立失效,称为独立失效组。

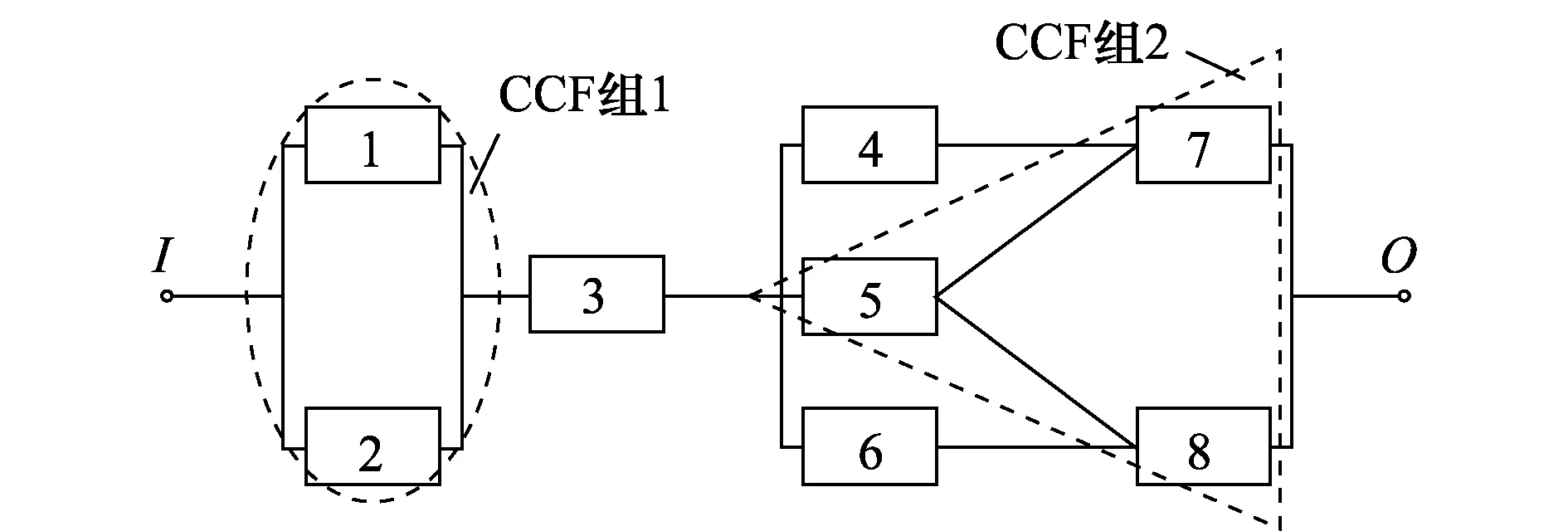
图3　系统可靠性框图和CCF组

事先已知1、2号元件,3、4、6号元件和5、7、8号元件在独立失效情况下的寿命服从指数分布,且失效率参数λ各不相同。为了对各元件的独立失效率进行估计,分别选取了50个元件进行失效观察。该试验为定时截尾寿命试验,观察时间为5 000 h。其失效时刻如表1～表3所示。同时,对两个CCF组分别进行CCF观察,并将多重失效时刻记录在表2和表3中。

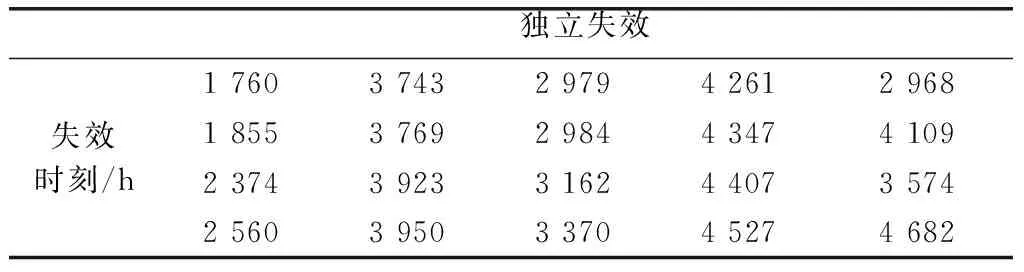
表1　独立组失效时刻

表2　CCF组1失效时刻

表3　CCF组2失效时刻

表4　失效数据及独立失效率计算值

表5　失效数据及CCF率计算值

现求解该系统的可靠度函数。设第i个元件的可靠度为Ri(t),i=1,2,…,8,则通过最小路集法和串并联法可得该系统可靠度函数为

RS=(R1+R2-R1R2)R3(R4R7+R5R7-

R4R5R7+R5R8-R5R7R8+R6R8-

R5R6R8-R4R6R7R8+R4R5R6R7R8)

(23)

式中,有3组相同分布单元:1、2号元件,5、7、8号元件和3、4、6号元件。令R1=R2=RA,R5=R7=R8=RB,R3=R4=R6=RC。则式(23)可写为

(24)

由式(13)可得到式(24)中各分量的表达式,即

图4显示了3种情况下的可靠性对比,其中完全CCF是指:只要发生共因就出现失效。由计算可知,不考虑CCF时,系统的期望寿命为5 132 h;不完全CCF为1 429 h;而在完全CCF的假设下只有805 h。可见,CCF会大大降低系统的期望寿命,在系统设计与维护中是不能忽视的因素。

图4　3种假设下系统可靠度对比

另外,进行贝叶斯更新可以更准确地对系统可靠性进行分析。在实际情况中,人们更关心系统可靠性的退化情况而非期望寿命,因此需要计算系统可靠度在何时会降低到指定数值。图5显示了在不完全CCF假设下,贝叶斯更新前后系统的可靠性退化情况。在更新前,系统可靠度在第165 h降至0.9,而更新后这一时刻则变为192 h,可见系统的可靠寿命比先验估计有所提高。

图5　贝叶斯更新前后的可靠度分位寿命

此外,经过贝叶斯更新后,不完全CCF系统的可靠度依次降至0.85和0.8的时刻分别为291 h和393 h。根据这些信息可以确定系统的检修周期。例如,若要使系统可靠性维持在85%以上,则应每间隔291 h检修一次。

本节实例分析表明,CCF会大大降低系统的可靠度,是实际分析中不能忽略的因素。另外,与传统的完全CCF相比,本文提出的不完全CCF假设能够更合理地对系统的可靠性进行分析。最后,贝叶斯更新能够更准确地反映系统的状态,并且可以通过新的数据来方便地进行动态更新。

4　结　论

参考文献：

[1] CHAE K C, CLARK G M. System reliability in the presence of common-cause failures[J]. IEEE Trans.on Reliability, 1986, 35(1):32-35.

[2] MANKAMO T, KOSONEN M. Dependent failure modeling in highly redundant structures—application to BWR safety valves[J]. Reliability Engineering & System Safety, 1992, 35(3): 235-244.

[3] DHILLON B S, ANUDE O C. Common-cause failure analysis of a parallel system with warm standby[J]. Microelectronics Reliability, 1993, 33(9): 1321-1342.

[4] VAURIO J K. An implicit method for incorporating common-cause failures in system analysis[J]. IEEE Trans.on Reliability, 1998, 47(2):173-180.

[5] 王家序,周青华,肖科,等.不完全共因失效系统动态故障树模型分析方法[J].系统工程与电子技术,2012,34(5):1062-1067.

WANG J X, ZHOU Q H, XIAO K, et al. Dynamic fault tree model analysis of systems subjected to incomplete common-cause failure[J]. Systems Engineering and Electronics, 2012, 34(5): 1062-1067.

[6] WANG C, XING L, LEVITIN G. Probabilistic common cause failures in phased-mission systems[J]. Reliability Engineering & System Safety, 2015, 144(12): 53-60.

[7] ZHU P, HAN J, LIU L, et al. A stochastic approach for the analysis of dynamic fault trees with spare gates under probabilistic common cause failures[J]. IEEE Trans.on Reliability,2015,64(3): 878-892.

[8] 阮渊鹏, 何桢. 基于MCS-CA的考虑共因失效的复杂系统可靠性评估[J]. 系统工程与电子技术, 2013, 35(4): 900-904.

RUAN Y P, HE Z. Reliability evaluation of complex systems with common cause failures based on MCS-CA[J]. Systems Engineering and Electronics, 2013, 35(4): 900-904.

[9] ZHU P, HAN J, LIU L, et al. Reliability evaluation of phased-mission systems using stochastic computation[J]. IEEE Trans.on Reliability, 2016, 65(3): 1612-1623.

[10] 陈瑶, 李峭, 赵长啸, 等. 基于OBDD的航空电子网络可靠性分析[J]. 系统工程与电子技术, 2013, 35(1): 230-236.

CHEN Y, LI Q, ZHAO C X, et al. OBDD-based reliability analysis for avionics networks[J]. Systems Engineering and Electronics, 2013, 35(1): 230-236.

[11] XING L, LEVITIN G, WANG C, et al. Reliability of systems subject to failures with dependent propagation effect[J]. IEEE Trans.on Systems, Man & Cybernetics:Systems,2013,43(2): 277-290.

[12] HAUGE S, HOKSTAD P, HABREKKE S, et al. Common cause failures in safety-instrumented systems: using field experience from the petroleum industry[J]. Reliability Engineering & System Safety, 2016, 151(7): 34-45.

[13] ZHANG M, ZHANG Z, MOSLEH A, et al. Common cause failure model updating for risk monitoring in nuclear power plants based on alpha factor model[J]. Journal of Risk & Reliability, 2017, 231(3): 209-220.

[14] YU Y, WANG S, NIU F. Analysis of common cause failure effect on system reliability in seismic PSA[J]. Progress in Nuclear Energy, 2014, 75(6): 158-167.

[15] FAN D, WANG Z, LIU L, et al. A modified GO-FLOW methodology with common cause failure based on discrete time Bayesian network[J]. Nuclear Engineering & Design, 2016, 305(11): 476-488.

[16] MECHRI W, SIMON C, BENOTHMAN K. Switching Markov chains for a holistic modeling of SIS unavailability[J]. Reliability Engineering & System Safety,2015,133(133):212-222.

[17] WANG J, LI M. Redundancy allocation optimization for multistate systems with failure interactions using semi-Markov process[J].Journal of Mechanical Design,2015,137(10):1-12.

[18] LIU Z, LIU Y, CAI B, et al. Dynamic Bayesian network mode-ling of reliability of subsea blowout preventer stack in presence of common cause failures[J]. Journal of Loss Prevention in the Process Industries, 2015, 38(6): 58-66.

[19] 张友鹏, 杨金凤. 基于动态贝叶斯网络的CTCS-3级ATP系统可靠性分析[J]. 铁道学报, 2017, 39(7): 79-86.

ZHANG Y P, YANG J F. Reliability analysis on ATP system of CTCS-3 based on dynamic bayesian network[J]. Journal of the China Railway Society, 2017, 39(7):79-86.

[20] PARK J H. Time-dependent reliability of wireless networks with dependent failures[J]. Reliability Engineering & System Safety, 2017, 165(9): 47-61.

[21] 金星, 洪延姬, 杜红梅. 共因失效系统的可靠性分析方法[M]. 北京: 国防工业出版社, 2008.

JIN X, HONG Y J, DU H M. Reliability analysis method of common cause failure system[M]. Beijing: National Defence Industry Press, 2008.