非平稳海杂波背景下子带分段ANMF检测器
时艳玲, 林毓峰, 梁丹丹
(南京邮电大学通信与信息工程学院, 江苏 南京 210003)
0 引 言
海杂波背景下的微弱动目标检测一直以来都是雷达目标检测领域的研究热点[1-5]。目前,基于能量累积形式的自适应相干累积检测器是一类普遍采用且行之有效的雷达目标检测方法[6-8]。对于相干累积检测器而言,其检测性能的优劣主要取决于判决时刻的输出信噪比(signal to noise ratio,SNR)的高低[9]。在目标回波脉冲满足相参的条件下,可以通过直接增加相干检测器的脉冲累积数目来提高输出SNR,从而改善检测性能。文献[9]指出,对M个等幅相参脉冲信号进行相干累积,可以使输出SNR提升为原来单脉冲信号输出SNR的M倍。因此,通过增加检测器的累积脉冲数目来提升检测性能是一种有效做法。此外,针对运动目标和海杂波在多普勒频移的差异,使用窄带滤波器组滤除非目标所在频域的杂波信号也是提高检测器输出信杂比(signal to clutter ratio,SCR)的有效措施[10]。
针对相干累积检测器,在高斯杂波背景下,Kelly提出了广义似然比检测器(generalized likelihood ratio test,GLRT)。文献[11]提出了自适应归一化匹配滤波器(adaptive normalized matched filter,ANMF),获得了较好的性能。此后,针对各种工作环境,一系列基于GLRT和ANMF的改进算法相继被提出。这其中包括适用于平稳海杂波环境的M-ANMF[11]、∑-ANMF[12],适用于部分均匀海杂波环境的递归ANMF(recursive ANMF,R-ANMF)[13]、递归对称ANMF(recursive persymmetric ANMF, RP-ANMF)[14],适用于正交干扰加高斯噪声环境的子空间GLRT(subspace-based GLRT, SGLRT)、子空间自适应匹配滤波检测器(subspace-based adaptive matched filter,SAMF)[15],适用于距离多普勒分布式目标检测的确定散射体模型GLRT (deterministic scatterer model GLRT, DSM-GLRT)、高斯散射体模型GLRT(Gaussian scatterer model GLRT, GSM-GLRT)[16]、双门限GLRT (dual threshold GLRT,DT-GLRT)[17-18]等。这些检测器大多由前置的杂波白化滤波器和后置的匹配滤波器构成,其在一个相干处理间隔(coherent process interval,CPI)内将目标回波构建为未知常数与多普勒导向矢量的乘积形式,并且要求杂波向量在CPI内必须保持平稳或近似平稳的特性。通常,满足目标回波信号与目标模型相匹配的时间间隔要长于海杂波的平稳时间。因此,自适应相干累积检测器的最佳累积时间取决于海杂波的平稳时间[19]。随着雷达分辨率的提高和入射余角的减小,海杂波出现海尖峰的概率增加,其幅度分布偏离高斯假设,出现较长的拖尾。这些海尖峰的出现可能使弱目标回波被淹没,造成漏检概率增大[20-21]。更为关键的是,高分辨率海杂波所具有的空时非平稳特性[22-23]极大地限制了相干累积检测器的检测性能。一方面,高分辨率海杂波的空间非平稳性限制了可用于杂波协方差矩阵估计的参考样本数目,进而限制了协方差矩阵的估计精度,导致杂波白化效果下降,SCR累积增益产生损失。另一方面,高分辨率海杂波的时间非平稳性直接限制了自适应相干累积检测器的累积时长。
为了提升自适应相干检测器在非平稳海杂波背景下的检测性能,学者们从不同角度入手,提出了一系列改进算法。文献[22] 指出子带分解不仅可以抑制带内外杂波,而且还能提高杂波短期平稳性,提出了子带ANMF检测器。文献[23]研究指出,海杂波的非平稳特性主要由纹理体现,强杂波子带数据的纹理具有显著的非平稳特性,弱杂波子带数据的纹理具有平稳特性。根据子带杂波的这一特点,文献[23]在子带ANMF的基础上提出了子带开关相干检测器,提高了子带ANMF协方差矩阵的估计精度。文献[19]针对非平稳海杂波对传统ANMF累积时长的限制,采用短时间序列分段累积的方式增加检测器的累积时间,提出组合ANMF(combined ANMF,C-ANMF)检测器,有效延长了传统ANMF检测器的累积时间。采用相同的时间累积方式,文献[20]提出了组合自适应广义似然比线性门限检测器(combined adaptive generalized likelihood ratio test-linear threshold detector,CA-GLRT-LTD),进一步验证了短时间序列分段累积在自适应相干累积算法中的有效性。
在非平稳海杂波背景下,传统ANMF的长时累积面临一系列困难。首先,在长时累积条件下,信号与模型之间产生失配。这其中包括由目标多普勒频移走动导致的目标信号与目标模型之间的失配,以及由海杂波时间非平稳特性导致的杂波信号与杂波模型之间的失配。其次,在长时累积条件下,目标可能出现跨距离单元的情况,对参考单元样本造成污染。再次,RMB(Reed I S,Mallett J D,Brennan L E)准则[24]指出,为保证较小的SCR损失,用于海杂波协方差矩阵估计的参考样本数目与累积脉冲数目的比值应尽可能大。但在现实工作环境中,受海杂波空间非平稳特性的限制,这一要求往往难以满足。为克服上述长时累积存在的困难,同时削弱强杂波对目标检测产生的干扰,本文对雷达回波数据采取频域分割与时域分段累积相结合的方式来改善传统ANMF在非平稳海杂波背景下的检测性能,提出基于子带分段的分段自适应归一化匹配滤波检测器(subband segmented adaptive normalized matched filter,SS-ANMF)。相比于CA-GLRT-LTD和C-ANMF,SS-ANMF不但拥有更为出色的检测性能,同时还具备目标多普勒频率跟踪的能力,有效弥补了C-ANMF无法处理变速目标的不足。
1 信号模型
在脉冲多普勒雷达中,海杂波背景下的动目标检测一般使用二元假设检验模型为
(1)
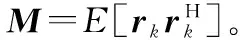
目前,非平稳海杂波多采用复合高斯模型进行建模[8,19-20,22-23]。当观测时间只有几微秒时,复合高斯模型退化为球不变随机向量(spherically invariant random vector,SIRV)模型,其表达式为
(2)
式中,τ代表纹理分量,反映海杂波功率;g代表散斑分量,反映海杂波的局部相关性。
目标模型构建为未知常数与多普勒导向矢量的乘积形式为
s=av(fd)
(3)
式中,幅度a是与目标雷达散射截面积有关的常数;v(fd)为多普勒导向矢量,定义为v(fd)=[1, exp(j2πfdTr), …, exp(j2π(N-1)fdTr)]T,fd表示目标多普勒频移,Tr表示雷达脉冲重复周期,上标T表示转置。
2 检测器设计
自适应相干检测器在非平稳海杂波背景下的检测性能受到强杂波干扰和累积时长有限的双重限制。本文提出的SS-ANMF检测器采用子带分解和短时间序列分段累积的方式分别克服上述两点限制。该检测器主要由4部分构成,如图1所示。
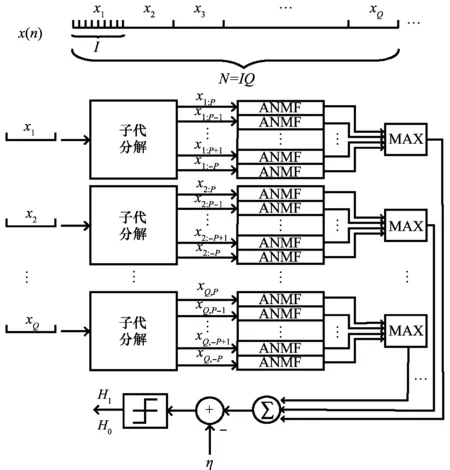
图1 SS-ANMF检测器流程图
图1中,4部分构成如下:
(1) 第1部分是原始雷达回波数据的预处理过程;
(2) 第2部分是前置的、包含2P+1个通道的线性相位离散傅里叶变换(discrete Fourier transform,DFT)调制滤波器组,其作用是实现对海杂波回波数据的子带分解;
(3) 第3部分是位于每个子带上的分段ANMF,其作用是构建子带杂波短时间序列对应的ANMF检测统计量;
(4) 第4部分是获得所有子带上、分段ANMF响应的最大值,然后再对Q个最大值求和,得到SS-ANMF检测统计量。其中,求最大值的作用是实现对目标多普勒频率的跟踪,求和的作用是实现长时累积。
2.1 预处理过程
在预处理过程中,将长度为N的雷达回波数据均匀分割为Q组长度为I的短时间序列,分割方式满足N=IQ,其中,Q为某一正整数。在短序列时段ITr内,目标回波采用式(3)进行建模,海杂波采用球不变随机矢量(spherically invariant randorn vector,SIRV)进行建模。经预处理之后,长时间序列对应的向量模型表示为
(4)
由于检测器是在短时间时段内对目标信号和杂波信号进行建模,因此信号和模型只需在短时间序列时段内满足匹配关系即可。此外,在短时间时段内,参考单元数目K将不再受限于累积脉冲数目N,而只与短时间序列长度I有关。故当I取值合适时,检测器不但可以获得较大的K/I,同时又不会影响累积脉冲数目N的设定。因此,短时间序列分段累积的方式能够有效解决自适应相干检测器在非平稳海杂波背景下进行长时累积的困难。
2.2 线性相位DFT调制滤波器组
本文使用文献[22]提出的线性相位DFT调制滤波器组实现回波数据的子带分解,该滤波器组由一组频域范围相互邻接的窄带滤波器[10]构成,通常要求滤波器组的频带宽度应覆盖观测目标信号的多普勒频移变化范围。雷达回波序列通过滤波器组后,生成与窄带滤波器一一对应的滤波数据,即为子带数据。因为杂波数据是按照多普勒频移的差异并经由不同的窄带滤波器滤出,所以目标信号与非目标子带杂波信号被有效分离,从而实现了对带外杂波的抑制。此外,由于子带杂波具有更高的短期平稳性[22-23],使得工作在子带杂波环境下的ANMF具备有累积更多脉冲数目的能力。接下来对线性相位DFT调制滤波器组的结构及其工作原理作简要介绍。
DFT调制滤波器组由低通原型滤波器h(l)调制而成,包含有2P+1个通道的DFT调制滤波器组的结构为
(5)
式中,p=-P, -P+1, …,P-1,P表示子带序号;H(ω)=∑h(l)e-jlw,其中,h(l)是通带位于[-π/(2P+1), π/(2P+1)]的低通原型滤波器。该滤波器组将多普勒频率区间[-0.5fr, 0.5fr]分解为2P+1个子带区间,其中,fr=1/Tr表示脉冲重复频率。第p个子带的多普勒频移范围为
(6)
将h(l)设置成线性相位、因果、有限冲激响应的滤波器,则所有的子带滤波器hp(l)都满足线性相位、因果、有限冲激响应的特性。通过将接收到的回波信号与hp(l)进行卷积,获得2P+1组子带回波时间序列,其表达式为
(7)
式中,*表示卷积;p=-P,-P+1,…,P-1,P。
子带分解后,式(1)转化为子带上2P+1个假设检验,其中第p个子带对应的假设检验表示为
(8)
第p个子带数据表示为
(9)
2.3 分段ANMF检测器
依据文献[11],ANMF检测器的表达式为
(10)
(11)
则位于第p个子带上的分段ANMF检测器可表示为
ξq;p(xq;p|p)=
fd∈Ωp;q=1,2,…,Q
(12)
其中
(13)
2.4 SS-ANMF检测器
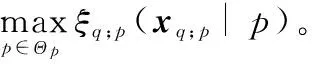
Θp=[-P,-P+1,…,P-1,P]
(14)
SS-ANMF检测器在预处理过程将雷达回波数据分割为短时间序列(N=IQ),克服了长时累积条件下信号与模型之间的失配以及K/I取值过小的问题;通过线性相位DFT滤波器组对雷达回波信号进行子带分解,削弱了杂波信号对检测目标的干扰;通过在短时间序列时段内,对2P+1个子带上的分段ANMF响应取最大值,实现了对目标多普勒频移的跟踪;最后通过对长时间序列时段内的Q个最大值求和,实现了长时累积的目的。
理论上,P的取值与检测器的工作性能有关。P取值越大,每个窄带滤波器的通带范围就越小,对杂波的抑制效果就越好,检测性能也会更佳,但这种检测性能的提升是以增加运算量为代价的。同样的,I、Q的取值也与检测器的工作性能相关。本文分析了传统ANMF、分段ANMF、SS-ANMF、CA-GLRT-LTD、C-ANMF的计算复杂度,从中获悉SS-ANMF相比于传统ANMF在计算量上的增加情况,以及I、Q、P的取值对上述检测器计算量的影响。由于暂时无法获得SS-ANMF关于虚警概率与检测门限的数学表达式。因此,SS-ANMF的门限由蒙特卡罗方法确定。此外,SS-ANNMF检测器能从多普勒频率角度实现对目标速度的跟踪,因此,该检测器不仅可以检测径向匀速目标,还可以检测变速目标。
3 实验结果与性能分析
实验采用实测海杂波数据来源于http:∥soma.mcmaster.ca/ipix.php,数据名为19980223-170435,雷达距离分辨率为15 m,采用HH极化。该数据有34个距离单元, 每个距离单元有59 945个回波脉冲,雷达脉冲重复频率fr为1 000 Hz。取实测海杂波数据的前31个距离单元用于实验,以第10个距离单元为CUT,其余30个距离单元为参考样本(K=30)。点目标使用式(3)进行仿真,实验中平均输入SCR定义为
SCRavg=10lg(a2/Pc)
(15)
式中,Pc是实测海杂波数据的平均功率。在给定虚警概率Pf=0.001条件下,检测门限由蒙特卡罗方法确定。每个检测器分别进行1 000次检测实验获得检测概率。
3.1 子带杂波功率的分布状况
通常,受海浪、风速等海况因素影响,海杂波能量会分布在零多普勒频移附近的一个很宽的频域范围内。因而,子带杂波序列的平均功率会各不相同。由于线性相位DFT调制滤波器组只是把原始杂波能量按照多普勒频移的不同分解到相应的子带上,因此分解得到的所有子带的杂波平均功率总和与原始杂波平均功率相等。此处取P=8,则前置DFT调制滤波器组将多普勒频移区间[-500 Hz, 500 Hz]分割成17个子带,其中第p个子带对应的多普勒频移范围为
p=-8,-7,…,-1,0,1,…,7,8
(16)
对原始杂波数据的平均功率作归一化处理,分别计算各个子带杂波的平均功率相对于原始杂波平均功率的比值,得到原始杂波平均功率在各子带上的分布情况,如图2所示。
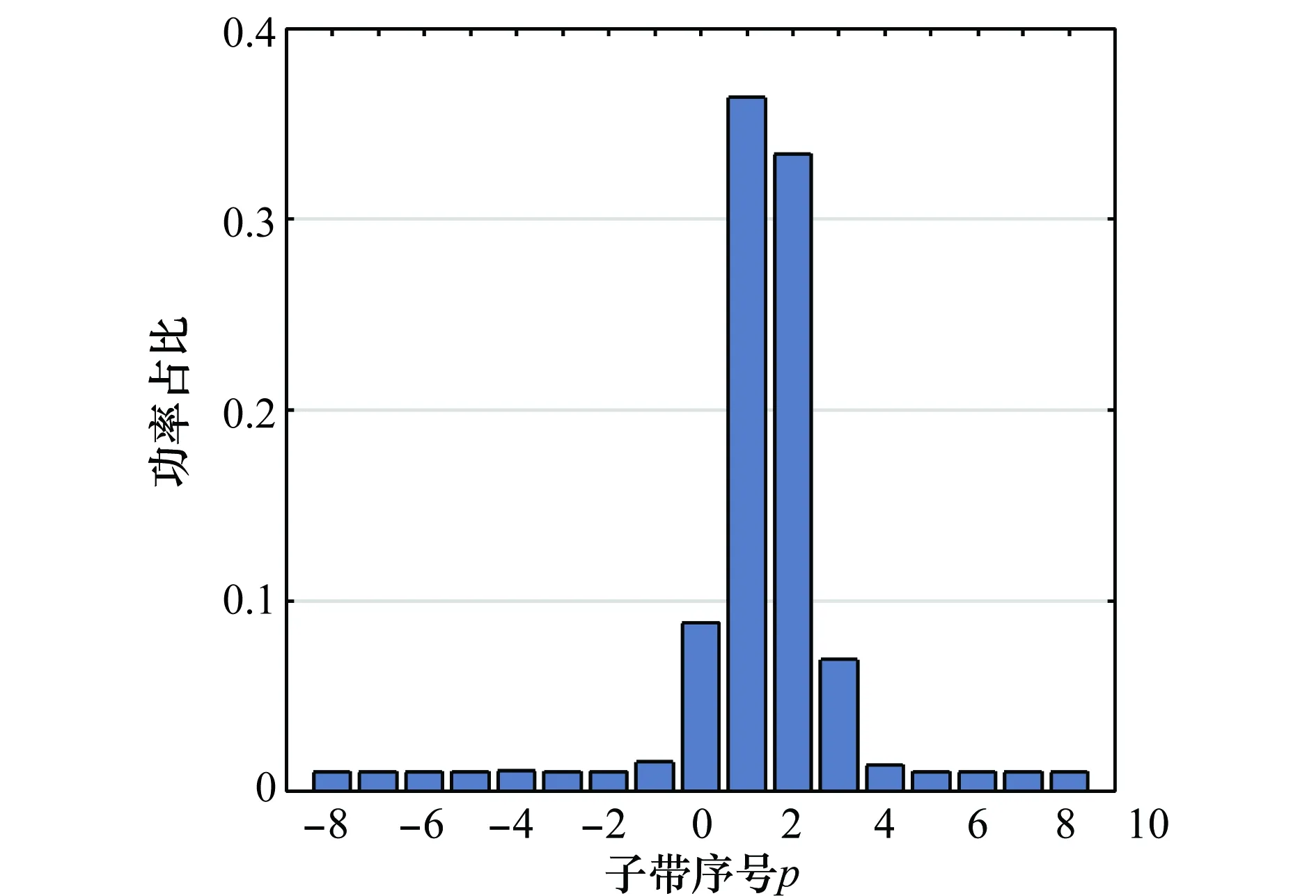
图2 子带杂波平均功率分布图
由图2可知,杂波能量主要集中在4个子带上(p=0,1,2,3),分别为两个强杂波子带(p=1,2)和两个临界杂波子带(p=0,3)。其余的13个子带的平均功率要远小于原始杂波的平均功率,为弱杂波子带。由于所有子带杂波的平均功率均小于原始杂波平均功率,所以无论目标信号的多普勒频移位于哪个子带,相应子带回波数据相比于原始杂波都会存在一定的输出SCR增益:强杂波子带的输出SCR增益小,弱杂波子带的输出SCR增益大。需要指出的是,对于ANMF检测器而言,不同多普勒频移的杂波分量对检测性能的影响程度是不同的:与目标信号多普勒频移越接近的杂波成分对检测器性能影响越大。由于窄带滤波器在滤取目标信号的同时,会不可避免地保留与目标多普勒频移相近的杂波分量,因而不能简单地将子带输出SCR增益看作是检测器的输出SCR增益。但由于子带输出SCR的提升是通过抑制带外杂波的方式获得的,因而子带输出SCR增益能够反映检测器输出SCR的提高。
3.2 子带分解对ANMF检测器的影响
本文通过构造子带ANMF检测器(去除SS-ANMF检测器的预处理过程),与ANMF进行对比,以验证子带分解具有的益处。根据图2给出的子带杂波平均功率分布图,将目标信号的多普勒频移fd设定为59 Hz、177 Hz、413 Hz,分别对应于子带p=1(强杂波子带),子带p=3(临界杂波子带),子带p=7(弱杂波子带)。参数设置为:K=30,P=8,依次取N等于4、8、12、16、20、24、28,得到不同N对应的检测性能曲线,如图3所示(为显示清晰,图3中只给出了N等于4、12、20、28时对应的检测性能曲线)。
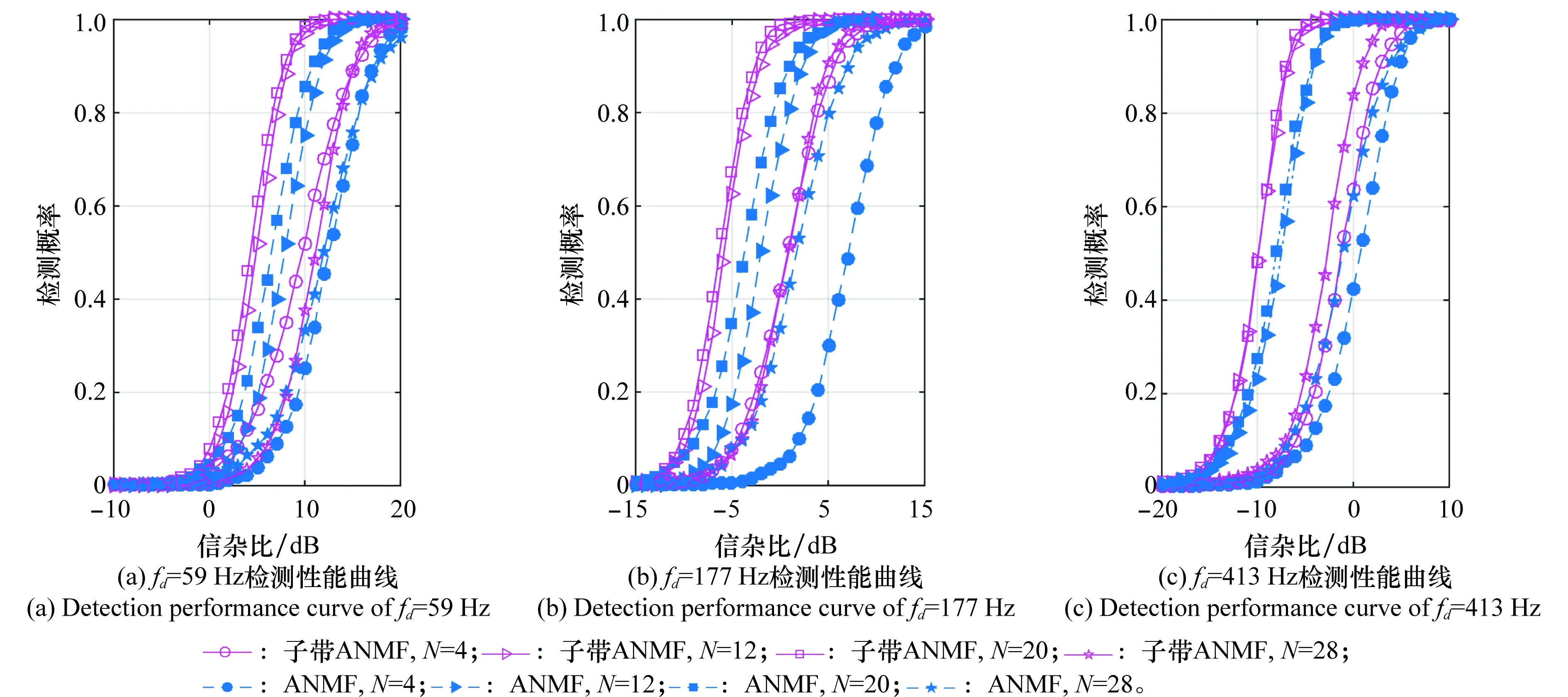
图3 子带ANMF、ANMF检测性能对比图
由图3可以看出:首先,子带ANMF和ANMF在fd=413 Hz时,检测性能最好;fd=177 Hz时,检测性能次之;fd=59 Hz时,检测性能最差。这说明两者的检测性能均受杂波强度的影响,目标多普勒频移附近的杂波强度越大,检测性能越差。其次,无论目标多普勒频移位于何种子带类型,子带ANMF的检测性能均要优于ANMF。最后,子带ANMF相对于ANMF的检测增益在不同的累积脉冲长度N下均存在。
为更加直观地比较子带ANMF与ANMF在不同累积脉冲长度下的检测性能,图4在3个多普勒频点处给出了两者在固定信杂比条件下,检测概率随累积脉冲长度N变化的折线图。
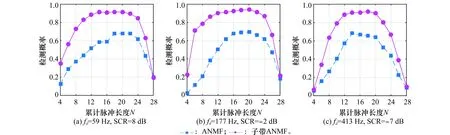
图4 在给定SCR条件下,ANMF与子带ANMF检测性能随累积脉冲长度N的变化曲线图
从图4可以看出:首先,两者的检测性能均随着N取值的增加,先改善后恶化。其次,在不同的累积脉冲长度N下,子带ANMF相比于ANMF均存在显著的检测增益,并且这种检测增益在积累时间约为18 ms(N=18)时达到最优。
3.3 短时间序列分段累积对ANMF检测器的影响
本文通过构造分段ANMF检测器(在ANMF基础上增加与SS-ANMF相同的预处理过程),与ANMF进行对比,以验证短时间序列分段累积具有的益处。实验参数设置为:K=30,P=8,依次取N等于8、12、16、20、24、28,I=4,Q由关系式N=IQ确定。图5显示了分段ANMF与ANMF的检测性能曲线。在图5的基础上,图6给出了检测概率等于0.9时,分段ANMF和ANMF的SCR增益随N的变化趋势(以N=4的输入SCR为基准)。
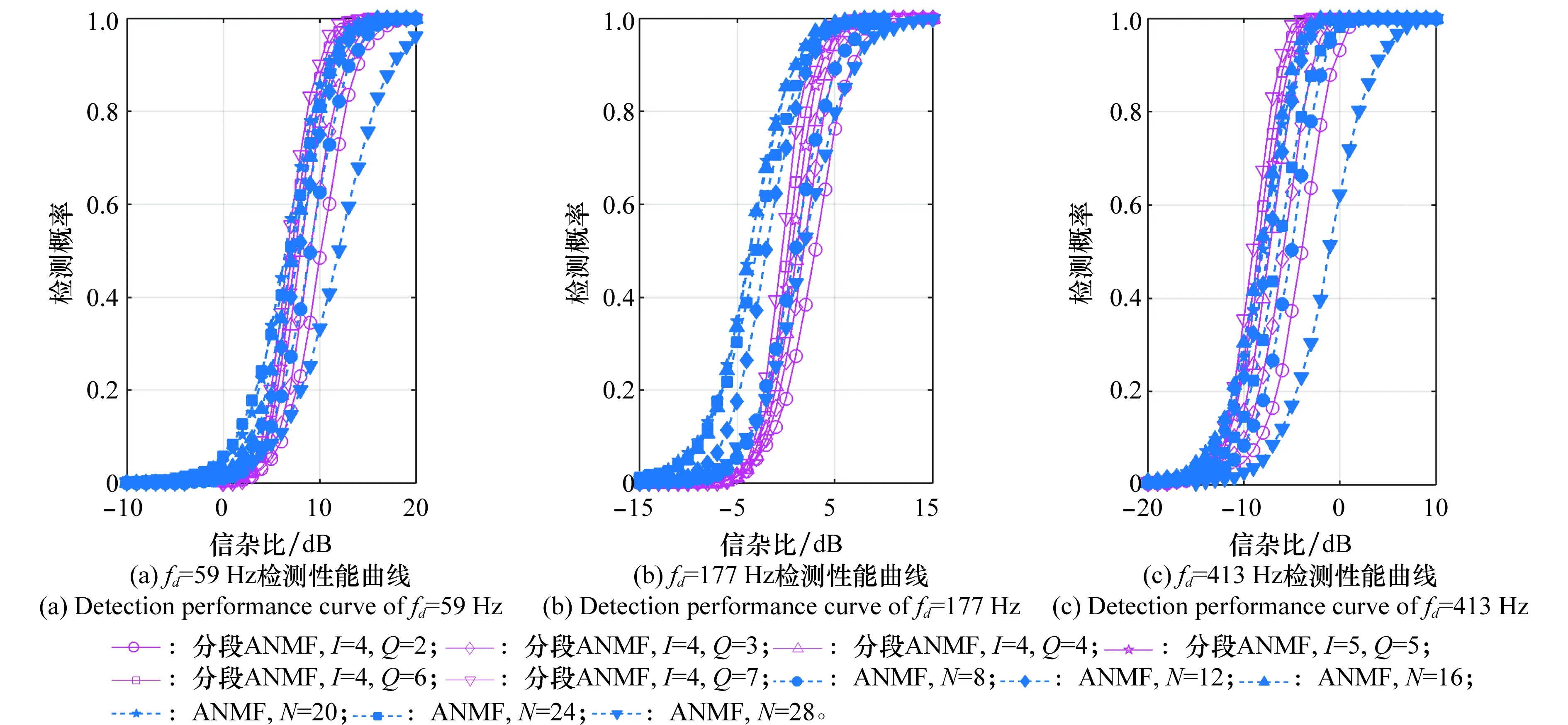
图5 分段ANMF与ANMF检测器随信杂比的变化曲线图
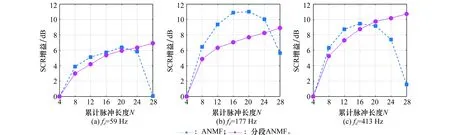
图6 检测概率为0.9时,信杂比增益与累积脉冲长度的关系变化图
由图5和图6可以看出:首先,在3个多普勒频点处,ANMF的检测性能先随着N的增大而改善,在N=18附近达到最佳,之后随着N的继续增加,ANMF检测性能逐步恶化。ANMF检测性能受累积脉冲长度、实测杂波与杂波模型之间的匹配程度、杂波协方差矩阵估计精度等一系列因素的共同影响。当N较小时,实测杂波与模型之间的匹配程度较好,杂波协方差矩阵估计准确度较高,因而检测器能够实现有效的相干累积;当N过大时,杂波与模型逐渐失配,杂波协方差矩阵估计准确度下降,检测器相干累积的有效性逐步恶化。ANMF检测性能先改善后恶化的现象充分反映了高分辨率海杂波的空时非平稳特性对传统自适应相干累积检测器累积时长的限制。其次,在N较小时,尽管分段ANMF与ANMF的累积脉冲长度相等,但在3个多普勒频点处,后者的检测性能均要优于前者。这说明相比于理想条件下的相干累积,分段累积的工作方式存在一定的SCR损失。但由于分段ANMF只需要保证短时间脉冲序列的有效累积,因而弥补了ANMF在长时累积时性能恶化的缺陷。从图6可以直观地看出,随着Q的增大,分段ANMF的SCR增益逐步增加,并最终超过了ANMF。最后,除了具备长时相干累积的能力,分段ANMF算法还在运算复杂度上占有优势。对于累积脉冲长度为N,参考样本数为K的ANMF,其计算复杂度为:O(KN2+N3)次复数乘法和O(KN)次复数加法。分段ANMF的计算复杂度为:O(KQI2+QI3)次复数乘法和O(KQI)次复数加法。由N=IQ可知,Q取得越大,分段ANMF的运算优势越显著。所以在图6中,两者的检测性能虽然在折线交点处达到相同,但此时的分段ANMF具有更小的计算复杂度。
3.4 SS-ANMF、CA-GLRT-LTD、C-ANMF检测性能比较
SS-ANMF检测器的特点是对子带分解算法和短时间序列分段累积算法的有机结合,其对上述两种信号处理方式的有效继承是SS-ANMF检测优势的基础。为体现SS-ANMF在非平稳海杂波环境下的有效性,接下来从计算复杂度和检测概率两方面,将SS-ANMF与已有的CA-GLRT-LTD、C-ANMF检测算法进行比较。
由图1可以看出,SS-ANMF的计算量主要由线性相位DFT调制滤波器组和ANMF两部分构成。其中DFT调制滤波器组的子带分解过程等效为I点快速傅里叶变换(fast Fourier transform,FFT)过程,其计算量为(1/2)Ilog2I次复数乘法和Ilog2I次复数加法。则SS-ANMF的计算复杂度可表示为O(Q(2P+1)(KI2+I3+(1/2)Ilog2I))次复数乘法,O(Q(2P+1)(KI+Ilog2I)+(Q-1))次复数加法。CA-GLRT-LTD、C-ANMF两个算法在多普勒频域采用2P+1点采样,则两者的计算复杂度都可近似表示为O(Q(2P+1)(KI2+I3)+(2P+1)(Q-1))次复数乘法和O(Q(2P+1)(KI))次复数加法。通过对比可以看出,SS-ANMF相较于对比算法所多出的计算量主要来自于线性相位DFT调制滤波器组引入的I点FFT过程。
接下来通过实验对比SS-ANMF与CA-GLRT-LTD、C-ANMF的检测性能。参数设置为:K=30,P=8,N=24,I=8,Q=3,CA-GLRT-LTD和C-ANMF的多普勒频移取值范围设定为fd= 0,±1/ITr,±2/ITr,…,±(0.5I)/ITr。图7显示了目标多普勒频率分别处于3种子带频域范围内时,SS-ANMF、CA-GLRT-LTD和C-ANMF的检测性能对比图。
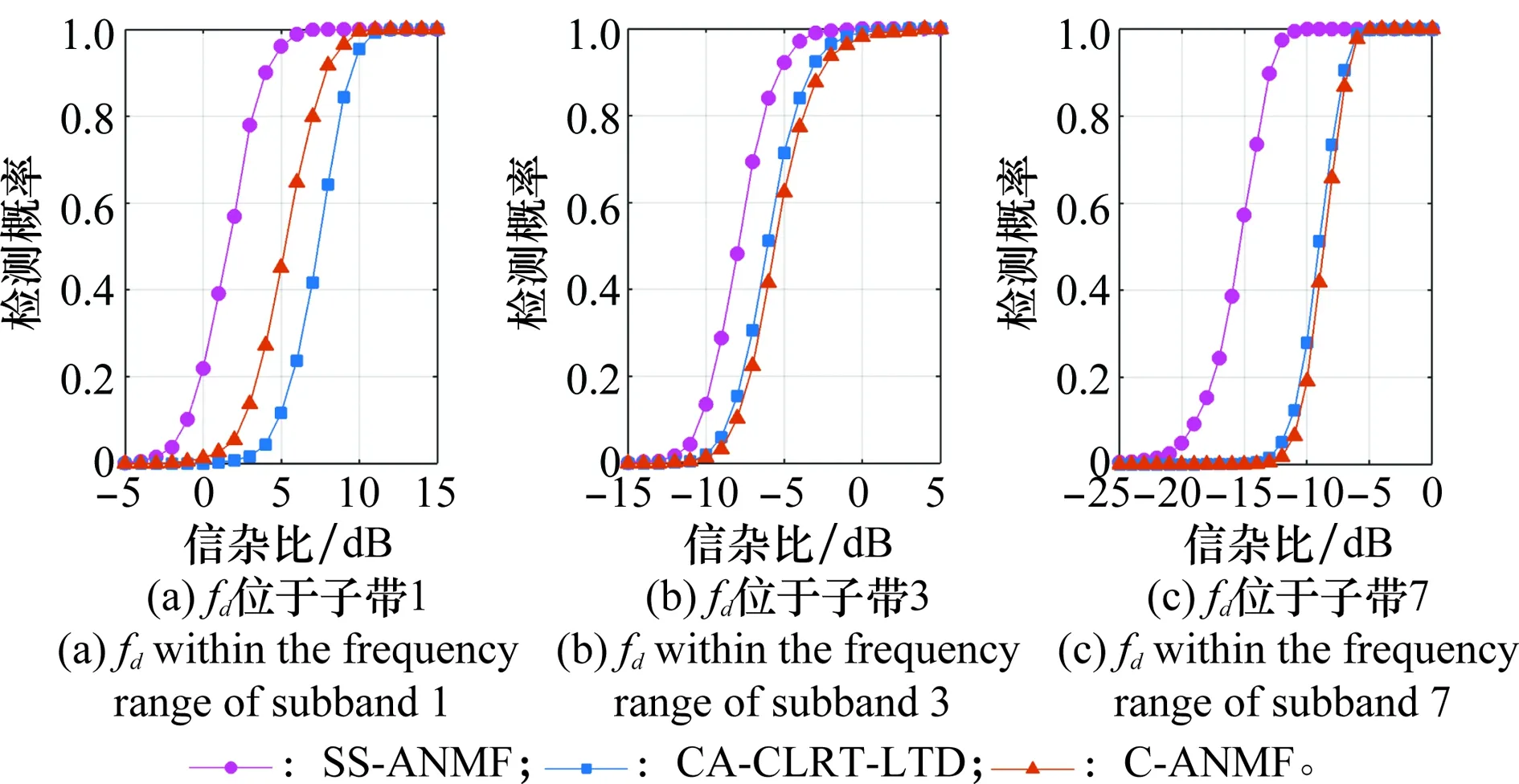
图7 SS-ANMF、CA-GLRT-LTD、C-ANMF检测概率对比图
从图7中可以看出,在强杂波子带(见图7(a))、临界杂波子带(见图7(b))和弱杂波子带(见图7(c))环境下,SS-ANMF相对于对比算法均存在至少2 dB的检测增益。此外,为了验证检测器在整个目标多普勒频域范围内的有效性,采用与图7相同的参数设置,在-500~500 Hz的频域内等间距地选取了17个频点,分别作为目标的多普勒频率,得到了在SCR=-5 dB 、SCR=0 dB、SCR=5 dB条件下,3种检测算法在不同目标多普勒频率的检测性能,如图8所示。
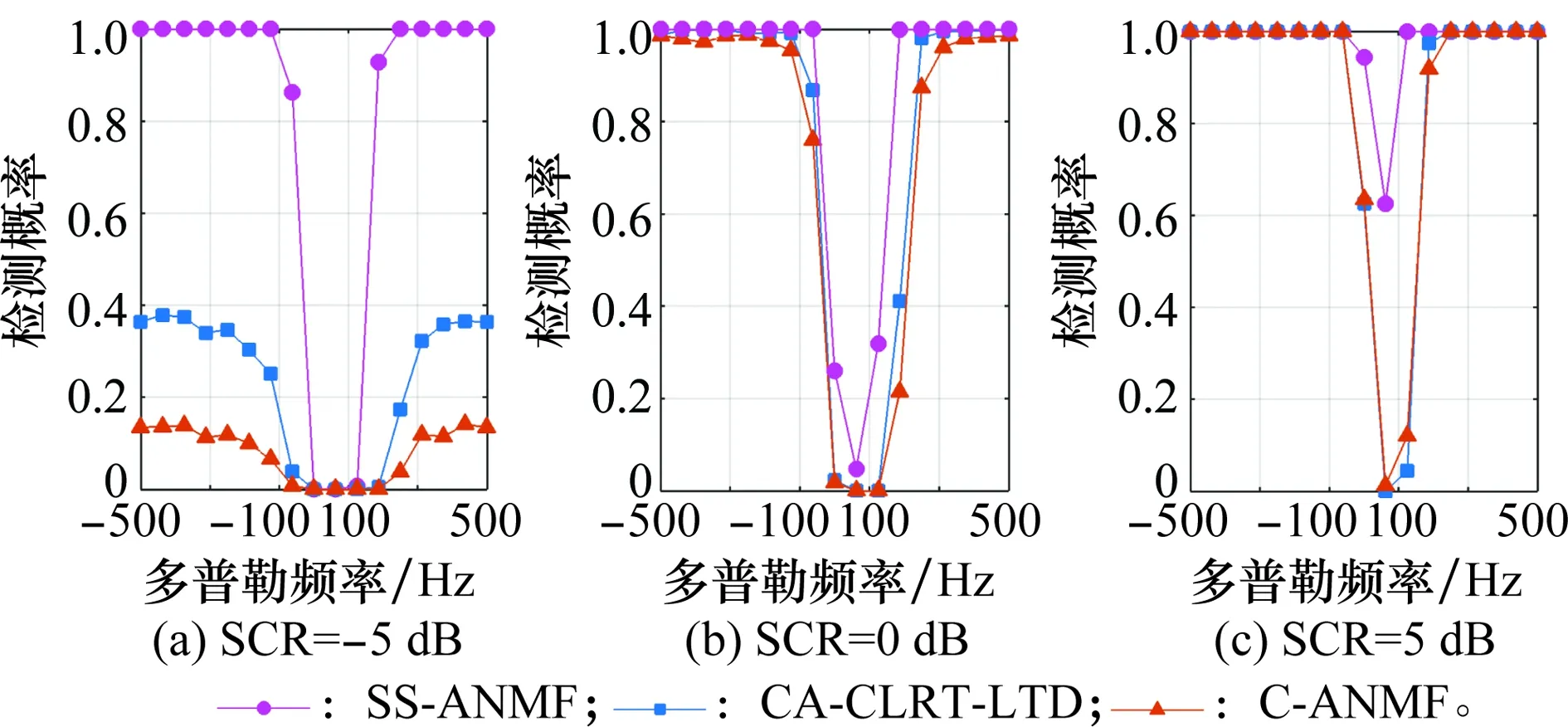
图8 在给定SCR条件下, SS-ANMF、CA-GLRT-LTD和 C-ANMF对不同目标多普勒频率的检测性能比较
图8(a)~图8(c)分别体现了SS-ANMF相比于对比算法,在弱杂波区、临界杂波区、强杂波区存在显著的检测增益。由于CA-GLRT-LTD和C-ANMF使用了短时间序列分段累积算法,而SS-ANMF同时使用了子带分解算法和短时间序列分段累积算法,所以SS-ANMF在图7和图8中所体现出的检测增益验证了SS-ANMF中子带分解算法的优势。
4 结 论
本文针对非均匀海杂波背景下的雷达微弱动目标检测问题,结合子带分解和短时间序列分段累积两种算法,提出了SS-ANMF检测器。通过对原始杂波进行子带分解,实现了带内外的双杂波抑制,不仅提高了目标所在子带的输出SCR,同时又提升了杂波的短期平稳性。通过短时间序列分段累积的方式,克服了传统自适应检测器长时间累积下的性能限制,使得检测器获得了更长的有效脉冲累积长度。通过实测的海杂波数据进行实验表明,子带分解算法和短时间序列分段累积算法能有效提高ANMF检测性能,SS-ANMF继承了上述两种算法的优势,其相比于CA-GLRT-LTD、C-ANMF具有更好的检测性能。
参考文献:
[1] LIU W J, XIE W C, WANG Y L. Adaptive detection based on orthogonal partition of the primary and secondary data[J]. Journal of Systems Engineering and Electronics,2014,25(1):34-42.
[2] CHEN X L, GUAN J, BAO Z H, et al. Detection and extraction of target with micromotion in spiky sea clutter via short-time fractional Fourier transform[J]. IEEE Trans.on Geoscience and Remote Sensing, 2014, 52(2):1002-1018.
[3] 赵宜楠,姜智卓,唐晨亮,等.复合高斯杂波中极化MIMO雷达的自适应检测[J].系统工程与电子技术,2015,37(11):2474-2479.
ZHAO Y N, JIANG Z Z, TANG C L, et al. Adaptive detection of polarimetric MIMO radar in compound-Gaussian clutter[J]. Systems Engineering and Electronics, 2015, 37(11):2474-2479.
[4] 范一飞, 罗丰, 李明. 海杂波AR谱多重分形特性及微弱目标检测方法[J]. 电子与信息学报, 2016, 38(2):455-463.
FAN Y F, LUO F, LI M. The multifractal properties of AR spectrum and weak target detection in sea clutter background[J].Journal of Electronics and Information Technology,2016,38(2):455-463.
[5] 郑作虎, 王首勇. 复杂海杂波背景下分数低阶匹配滤波检测方法[J]. 电子学报, 2016, 44(2): 319-326.
ZHENG Z H, WANG S Y. Radar target detection method of fractional lower order matched filter in complex sea clutter background[J]. Acta Electronica Sinica, 2016, 44(2): 319-326.
[6] 谢洪森,邹鲲,杨春英,等.海杂波协方差矩阵估计及其对目标检测性能的影响[J].系统工程与电子技术,2011,33(10):2174-2178.
XIE H S, ZOU K, YANG C Y, et al. Sea clutter covariance matrix estimation and its impact on signal detection performance[J].Systems Engineering and Electronics,2011,33(10):2174-2178.
[7] MCDONALD M K, CERUTTI-MAORI D. Coherent radar processing in sea clutter environments, part 2: adaptive normalised matched filter versus adaptive matched filter performance[J]. IEEE Trans.on Aerospace and Electronic Systems,2016,52(4): 1818-1833.
[8] 施赛楠,水鹏朗,刘明.基于复合高斯杂波纹理结构的相干检测[J].电子与信息学报,2016,38(8):1969-1976.
SHI S N, SHUI P L, LIU M.Coherent detection based on texture structure in compound-Gaussian clutter[J]. Journal of Electronics and Information Technology, 2016, 38(8): 1969-1976.
[9] 丁鹭飞,耿富录. 雷达原理[M]. 3版. 西安:西安电子科技大学出版社, 2002: 138-141.
DING L F, GENG F L. Radar principles[M]. 3rd ed. Xian: Xidian University Press, 2002: 138-141.
[10] 张明友,汪学刚. 雷达系统[M]. 2版. 北京:电子工业出版社, 2011: 105-108.
XUE M Y, WANG X G. Radar system[M]. 2nd ed. Beijing: Publishing House of Electronics Industry, 2011: 105-108.
[11] CONTE E, LOPS M, RICCI G. Adaptive detection schemes in compound-Gaussian clutter[J]. IEEE Trans.on Aerospace and Electronic Systems, 1998, 34(4):1058-1069.
[12] GINI F, GRECO M V. Suboptimum approach to adaptive coherent radar detection in compound-Gaussian clutter[J]. IEEE Trans.on Aerospace and Electronic Systems, 1999, 35(3):1095-1104.
[13] CONTE E, DE MAIO A, RICCI G. Covariance matrix estimation for adaptive CFAR detection in compound-Gaussian clutter[J]. IEEE Trans.on Aerospace and Electronic Systems, 2002, 38(2):415-426.
[14] CONTE E, MAIO A D. Mitigation techniques for non-Gaussian sea clutter[J].IEEE Journal of Oceanic Engineering,2004,29(2): 284-302.
[15] LIU W, WANG Y L, LIU J, et al. Design and performance analysis of adaptive detectors for subspace signals in orthogonal interference and Gaussian noise[J]. IEEE Trans.on Aerospace and Electronic Systems, 2017, 52 (5): 2068-2079.
[16] BON N, KHENCHAF A, GARELLO R. GLRT subspace detection for range and Doppler distributed targets[J]. IEEE Trans.on Aerospace and Electronic Systems, 2008, 44(2): 678-696.
[17] 关键, 张晓利, 简涛, 等.分布式目标的子空间双门限GLRT CFAR检测[J]. 电子学报,2012, 40(9): 1759-1764.
GUAN J, ZHANG X L, JIAN T, et al. Dual-threshold CFAR detection for distributed targets[J]. Acta Electronica Sinica, 2012, 40(9): 1759-1764.
[18] 胡勤振, 苏洪涛, 周生华,等. 多基地雷达中双门限CFAR检测算法[J]. 电子与信息学报, 2016, 38(10):2430-2436.
HU Q Z, SU H T, ZHOU S H, et al. Double threshold CFAR detection for multisite radar[J]. Journal of Electronics and Information Technology, 2016, 38(10):2430-2436.
[19] XU S W, SHUI P L, YAN X Y, et al. Combined adaptive normalized matched filter detection of moving target in sea clutter[J].Circuits Systems and Signal Processing,2017,36(6):2360-2383.
[20] 刘明, 水鹏朗. 海杂波背景下的组合自适应GLRT-LTD[J]. 电子与信息学报, 2015, 37(12):2984-2990.
LIU M, SHUI P L. Combined adaptive GLRT-LTD against sea clutter[J].Journal of Electronics and Information Technology, 2015, 37(12):2984-2990.
[21] KEITH W, ROBERT T, SIMON W. 海杂波:散射、K分布和雷达性能[M]. 2版. 北京:电子工业出版社, 2016:16-17.
KEITH W, ROBERT T, SIMON W. Sea clutter: scattering the K-distribution and radar performance[M]. 2nd ed. Beijing: Publishing House of Electronics Industry, 2016:16-17.
[22] SHUI P L, SHI Y L. Subband ANMF detection of moving targets in sea clutter[J].IEEE Trans.on Aerospace and Electronic Systems, 2012, 48(4): 3578-3593
[23] 时艳玲. 非平稳海杂波背景下子带开关相干检测器[J]. 电子学报, 2014, 42(10): 1925-1931.
SHI Y L. A subband switching coherent detector in non-stationary sea clutter[J]. Acta Electronica Sinica, 2014, 42(10):1925-1931.
[24] REED I S, MALLETT J D, BRENNAN L E. Rapid convergence rate in adaptive arrays[J]. IEEE Trans.on Aerospace and Electronic Systems, 1974, 10(6):853-863.

