基于稀疏重构的TOA定位估计算法

胡进峰, 谢　浩, 李朝海, 李会勇, 谢菊兰

(电子科技大学电子工程学院, 四川 成都 611731)

0　引　言

用来波到达时间(time-of-arrival, TOA)对目标进行定位本质上是一个非线性估计问题。目前,常见的TOA定位估计算法有两类。第一类是泰勒级数法[1-4],该算法用一阶泰勒级数展开对非线性方程进行线性化处理,其收敛性十分依赖初始值的选取,当目标函数高度非线性并且在初始值选取不理想的情况下,收敛性难以保证;第二类为基于最小二乘法(least squares, LS)的TOA定位估计算法,包括标准LS[5]、加权LS(weighted LS, WLS)[6]、两级加权LS[7]等。其中,文献[8]提出了一种具有约束条件的加权LS估计(constrained weighted LS, CWLS),其估计结果较标准LS有了较大的提升,然而由于该算法只是利用了单次TOA样本进行估计,因此其估计结果易受噪声影响,估计的精度与稳定性依然有待提高。综上所述,已有的大部分TOA估计算法的定位精度都有待进一步提高;并且大都只是利用单次TOA进行估计,因此其定位结果受噪声影响较大。

针对上述问题,注意到TOA定位中,目标在空间中是稀疏的,本文提出将TOA定位问题转换成一个稀疏重构问题,并给出了基于贝叶斯准则的求解算法。所提方法可以对多样本进行联合估计,从而提高了定位精度与稳定性。

1　TOA定位估计原理

TOA定位估计原理是:通过测量移动端(mobile station, MS)到各基站(base stations, BSs)之间的单向传播时间来得到一组经过MS且以BSs为圆心的圆方程组,TOA定位估计问题就转换为了求解一组非线性圆方程的问题。但是由于方程组的高度非线性性,以及噪声对TOA的影响,导致对其进行精确定位难度极高。

假设(x,y)为目标坐标,已知第i个基站坐标为(xi,yi)(i=1,2,…,M),其中，M为接收信号的总基站个数。因此,不考虑测量误差,目标与各基站之间的距离定义为

(1)

发射信号由目标单向传播至各基站的时间为

(2)

式中,c为光速。因此,考虑测量误差，基于传播时间ti的相对距离ri定义为

ri=di+ei,i=1,2,…,M

(3)

式中,ei为第i个基站的测量误差。设每个基站的测量误差ei为零均值,方差为σ2的高斯白噪声。将式(3) 两边同时平方得到

(4)

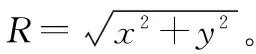
Aθ=b

(5)

2　基于多样本的稀疏重构算法

在第1节所描述的TOA定位估计原理中,注意到目标在空间中是稀疏的,因此本文提出将TOA定位求解问题转换为一个稀疏重构问题,并进一步给出了一种基于贝叶斯准则的求解算法。该算法可以对多样本进行联合估计,从而提高定位的精度和对噪声的稳健性。

2.1　方程的线性化

TOA定位原理中,定位模型是一个非线性方程组,无法用稀疏凸优化方法求解。因此,首先要将其线性化,线性化方法如下:

F(h)=F(hn)+F′(hn)(h-hn)T+J

(6)

由式(6)可知,目标真实坐标h为

h=hn+βn

(7)

TOA定位问题就转化成了估计hn和βn的问题。下面进一步给出基于稀疏算法的hn和βn的求解方法。令G=[F(h1),F(h2),…,F(hN)],Q=[F′(h1),F′(h2),…,F′(hN)],β=[h-h1,h-h2,…,h-hN]T,则式(6)可表示为

F(h)=(G+Qdiag(β))s(h)+J

(8)

根据式(8),可以估计出s(h),便可得到距离目标最近的网格点位置;估计出β,便可以得到目标偏离网格点的距离。最后,结合距离目标最近的网格点坐标与网格偏移距离便可得到目标最终位置的精确估计。

2.2　目标坐标的稀疏贝叶斯求解

2.2.1离目标最近的网格点hn的求解

定义CN(u|μ,∑)为一个复高斯分布的概率密度函数,其均值为μ=E{u},方差为∑=E{(u-μ)(u-μ)H}。

(9)

式中,E=[e(1),e(2),…,e(T)]。可以得到B=[b(1),b(2),…,b(T)]也为复高斯分布,即

式中,S=[s(t),…,s(T)];Φ=G+Qdiag(β)。

对于稀疏矩阵S,其复高斯先验概率分布为

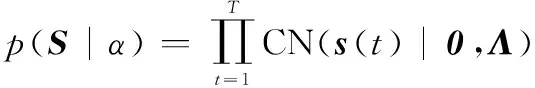
(10)

式中,Λ=diag(α),α=[α1,α2,…,αN]T∈RN。定义α的概率密度为Gamma超先验分布为

(11)

式中,ρ∈R,Γ(u|a,b)=[Γ(a)]-1baua-1exp(-bu)。

网格偏移距离β服从均匀分布,即

(12)

p(α0|c,d)=Γ(α0|c,d)

(13)

式中,c,d∈R。

通过以上推导,可以得到联合分布函数为

p(S,B,α0,α,β)=

p(B|S,α0,β)p(S|α)p(α)p(α0)p(β)

(14)

式(14)右边的概率密度函数由式(10)～式(13)定义。利用式(14)便可以得到S的后验概率分布为

(15)

最后把Σ与u代入式(16)计算,其峰值所在的网格点,就是距目标最近的网格点hn。

(16)

2.2.2偏移量的迭代计算

(17)

(18)

其中

求取E{lgp(S|B,α0,α,β)p(β)}的最大值的更新估计计算式为

βTPβ-2VTβ+Const

(19)

式中

(20)

R{diag(QHG∑)}

(21)

可以得到

(22)

2.3　总的算法流程

本文算法首先通过空间网格点的划分与一阶泰勒级数展开,将非线性方程组线性化,构建可以用稀疏重构求解的线性化的TOA定位估计模型。然后用基于贝叶斯准则的迭代求解估计目位置。在每一次迭代中,首先通过α0、α、β得到均值Σ与方差u的进一步估计,从而得到S的后验概率分布,然后,由式(17)、式(18)、式(22)分别得到α0、α、β的进一步的迭代更新估计值,并将其作为下一次Σ与u估计的输入参数。在迭代终止后,通过寻找式(19)的峰值所在的网格点确定距离目标最近的网格点坐标,并结合偏移距离矩阵β得到目标坐标。本文算法的流程如图1所示。

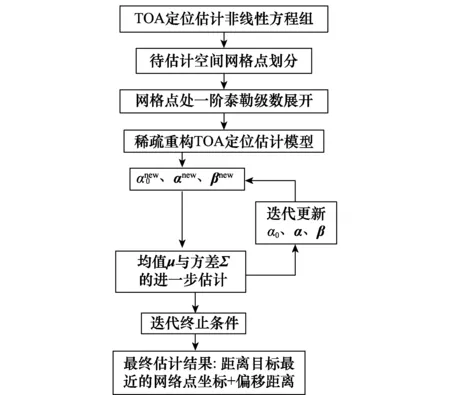
图1　本文算法流程图

3　仿真分析

将本文所提方法与标准LS算法和文献[8]中的CWLS算法进行对比仿真分析,仿真结果表明:①在利用单次样本到达时间的情况下,与LS算法相比,本文算法精度更高;②在多样本(多个来波到达时间)的情况下,本文算法通过联合估计抑制噪声影响,所提算法的精度和稳健性都高于LS算法与CWLS算法。

3.1　基于单次来波到达时间的仿真分析

仿真场景:5个基站,其坐标分别为:[0,0]m,[500,-500]m,[0,500]m,[-500,500]m,[-500 -500]m,[0,-500]m,[500,0]m。目标位于(225,335) m,平均噪声功率均为25 dBm2。所有结果均为独立的1 000次估计结果。本文以圆概率误差(circular error probable, CEP)作为评价定位准确性的参数。仿真表明,单样本TOA的情况下,与LS算法相比,本文算法精度更高。目标位置估计图如图2所示。

图2(a)为LS的估计仿真结果,图2(b)为文献[8]中CWLS估计的仿真结果。从图2(a)和图2(b)可以看出:LS估计的圆概率误差为21.543 9m,CWLS估计的圆概率误差为13.168 5m。

图2(c)和图2(d)是本文算法的仿真结果。首先将估计范围设置为500 m×500 m,网格间距设置为20 m,其CEP为28.456 1m,如图2(c)所示。在此基础上,进一步缩小估计范围与网格间距,在初次估计的结果上,将估计范围缩小为50 m×50 m,网格间距缩小为2 m。其CEP减小为17.8947m,如图2(d) 所示。其CEP比LS算法小,因此估计精度比LS算法高。

图2　目标位置估计

3.2　基于多次TOA的仿真分析

对本文算法在多样本的情况下进行仿真分析。结果表明,与标准LS算法及文献[8]中的CWLS算法相比,本文算法可以在多样本情况下进行联合估计,并且所提算法精度高于CWLS算法。

仿真场景同第3.1节。图3为来波到达时间样本数为10、估计范围为500 m×500 m、网格间距为20 m时本文算法的仿真结果。图3中,本文所提算法的CEP=8.740 3 m,该精度高于LS估计的21.543 9 m以及文献[8]中CWLS估计的13.168 5 m。图4为不同信噪比情况下,本文算法同LS、CWLS仿真结果的对比曲线。

图3　样本数为10的联合估计结果

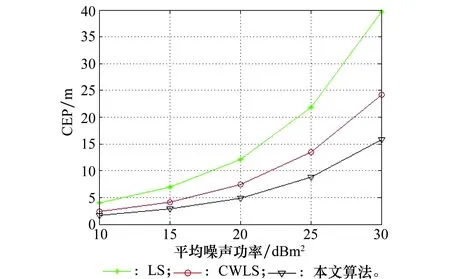
图4　本文算法与LS、CWLS对比曲线

由以上仿真结果可以得出结论:在单次TOA的情况下,本文算法相比于LS算法其定位精度更为精确,略低于CWLS算法;而在有多次TOA样本的情况下,通过本文算法对多样本进行联合估计,其定位精度高于LS算法与CWLS算法。

4　结　论

提出了一种稀疏重构TOA定位模型,并针对该模型给出了一种基于贝叶斯准则的求解算法。仿真结果表明,本文所提出的算法虽然在单样本TOA的情况下其估计精度并非最优,但是在具有多样本TOA的情况下,相比于其他已有的TOA算法估计精度和稳定性均有了十分明显的提高。

参考文献：

[1] YIN J H, WAN Q, YANG S W,K. et al. A simple and accurate TDOA-AOA localization method using two stations[J].IEEE Signal Processing Letters,2015,23(1):144-148.

[2] YOUSEFI S, CHANG X W, CHAMPAGNE B. Mobile localization in non-line-of-sight using constrained square-root unscented Kalman Filter[J]. IEEE Trans.on Vehicular Technology, 2015, 64(5):2071-2083.

[3] NI W, COLLINGS I B, WANG X, et al. Radio alignment for inductive charging of electric vehicles[J]. IEEE Trans.on Industrial Informatics, 2015, 11(2):427-440.

[4] CHEN C S. Hybrid TOA/AOA geometrical positioning schemes using linear lines of position for mobile location[J]. IEICE Trans.on Fundamentals of Electronics Communications & Computer Sciences, 2015, E98.A(8):1676-1679.

[5] CAFFERY J J. A new approach to the geometry of TOA location[J]. IEEE Trans.on Aerospace and Electronic Systems,1976,12(2):187-194.

[6] 朱国辉,冯大政,向平叶,等.传感器误差情况下的线性校正TOA定位算法[J].系统工程与电子技术,2015,37(3):498-502.

ZHU G H, FENG D Z, XIANG P Y, et al. Linear-correction TOA localization algorithm with sensor location errors[J]. Systems Engineering and Electronics, 2015, 37(3):498-502.

[7] CHEN C H, FENG K T. Enhanced distance and location estimation for broadband wireless networks[J]. IEEE Trans.on Mobile Computing, 2015, 14(11):2257-2271.

[8] CHEUNG K W, SO H C, MA W K, et al. Least squares algorithms for time-of-arrival-based mobile location[J]. IEEE Trans.on Signal Processing, 2004, 52(4):1121-1130.