基于离散时间贝叶斯网络的动态故障树分析的改良方法
兰 杰, 袁宏杰, 夏 静
(北京航空航天大学可靠性与系统工程学院, 北京 100191)
0 引 言
故障树分析作为极其重要的系统可靠性分析方法,已广泛应用于电子通信、医疗、能源、军事和航空航天等领域。传统静态故障树分析方法只重视部件间的与、或、表决等静态特性,而忽略了部件间的优先关系、顺序关系、功能相关性等动态失效特性,因此在分析具有动态失效特征的系统可靠性时存在较大误差[1]。为了弥补静态故障树分析方法在动态特性上建模功能的不足,文献[2]提出了动态故障树分析方法,以Markov理论为基础,建立了动态故障树模型。但Markov方法只适用于指数分布[3-4],而且存在状态空间爆炸问题,难以适用于大型动态故障树的分析。为避开Markov模型来解决动态故障树,文献[5]提出了基于复合梯形积分的计算方法,但该方法仍然存在组合爆炸的问题。
贝叶斯网络技术(Bayesian networks, BN)因具有系统建模、推理和诊断的优点[6-8],广泛应用于可靠性分析领域。2001年,文献[9]提出了静态故障树转化为BN的方法,并给出BN方法的实例。2005年,文献[10-11]提出了基于BN解决动态故障树的方法,在建模和分析能力方面有着显著优势,有效地避免了状态爆炸问题。文献[12-13]提出了动态BN分析方法,并给出了优先与门、温备份门等动态门转化为动态BN的方法。2007年,为了克服静态或均匀离散带来的精度差、效率低等问题,文献[14]提出了动态离散化的方法。2010年,文献[15]提出了联合动态离散化算法和基于事件的BN建模的方法,来提高服从任何分布的复杂系统的计算精度,但计算和迭代过程复杂。
传统的离散时间BN(discrete time Bayesian networks, DTBN)方法的计算时间、精度和效率受离散的时间分段n影响极大。针对此问题,本文基于复合梯形积分方法[5],分析讨论了传统方法计算的误差来源,并提出了新的动态门转化方法。与传统方法和Markov方法相比,新的转化方法补偿了传统方法的计算误差,提高了结果的计算精度和计算效率,适用于服从各种常见分布的复杂系统。最后以某测量系统为例,建立了系统的动态故障树和BN,验证了改良方法的可行性和高效性。
1 DTBN
DTBN是一个有向无环图,主要包括两部分:一部分是由有向边和节点构成的网络;另一部分是与每个节点相关的条件概率表(conditional probability table, CPT)。
将动态故障树中每个基本事件、静态或动态逻辑门和顶事件,用单独的BN节点来代替;用有向边来代表两个节点之间存在逻辑关系。如果节点A到节点B之间有一条A指向B的有向边,则节点A是B的父节点,B是A的子节点。对于给定节点Vi,拥有父节点pa(Vi),则:P(Vi|V1,V2,…,Vi-1)=P(Vi|pa(Vi))。
每一个节点都有其相关的条件概率表CPT。由BN的条件独立性可知,每一个节点的CPT可以由P(Vi|pa(Vi))得到,它描述了节点之间的逻辑关系。
把整个任务工作时间[0,t]分成n个均匀的区间,每个区间的长度为Δ=t/n,整个任务时间被划分n+1个部分:[0,Δ],[Δ,2Δ],[2Δ,3Δ], …,[(n-1)Δ,nΔ],[nΔ,+∞]。设节点E=[(x-1)Δ,xΔ],则节点E在[(x-1)Δ,xΔ]区间内失效,或称节点E处于状态x。若顶事件ET失效,则必然发生在这(n+1)个时间区间中。顶事件ET在任务时间[0,T]内失效的概率为

2 动态故障树转化的误差分析与补偿
2.1 优先与门转化分析
2.1.1传统的优先与门转化方法
优先与门有两个输入事件,当且仅当A失效,然后B失效,其输出C才会失效。优先与门的输入可以是基本事件,也可以是一个动态故障树的子树。优先门向DTBN的转化图如图1所示。

图1 优先与门转化为DTBN
将[0,t]分为n段,每段区间为Δ=t/n,则当A的概率密度为fA(t)时,A在状态x的失效概率为

(1)
式中,A可以服从任何概率分布。
不妨设A的失效概率服从指数分布,失效率为λa,则概率密度fA(t)=λae-λat。B的失效概率也服从指数分布,失效率为λb,概率密度fB(t)=λbe-λbt。可得A、B在状态x下的失效概率为

(2)
Pb,x=P(B=[(x-1)Δ,xΔ])=(eλbΔ-1)e-λbxΔ
(3)
当A、B在时间段[T,∞)内失效,即A、B位于n+1状态下的失效概率为
(4)
(5)
由优先与门性质可知,当且仅当A失效,然后B失效,其输出C才会失效。传统的贝叶斯转化方法设定:如果节点A和节点B在同一个时间区间[(x-1)Δ,xΔ]内失效,即A、B同时处于状态x时,节点C的失效概率直接为0,或者为1[16]。
若将A、B、C的工作时间[0,T]分为n段,则A的CPT为1×(n+1)行列的表,B的CPT为1×(n+1)行列的表,C的CPT为(n+1)×(n+1)×(n+1)的表。节点C的条件概率分布式为


(6)
当A、B中有任一个节点位于n+1状态,即在时间区间[T,∞)内失效,C节点在时间区间[T,∞)内失效的条件概率为1。
对单一优先门,若只需求得节点C在任务时间[0,T]的失效概率和可靠度时,可简化C的CPT的规模,设定节点A、B工作时间[0,∞)分为n+1段,节点C的时间区间分为[0,T]、[T,∞)两段。此时节点C的CPT为2×(n+1)×(n+1)的表,规模大幅度变小,且计算结果与第3.1节方法的结果一样。节点C在任务区间[0,T]失效,则条件概率表分布式为
PT,x,y=P(C=[0,T]|
A=[(x-1)Δ,xΔ],B=[(y-1)Δ,yΔ])=

(7)
PT,x,n+1=P(C=[0,T]|A=
[(x-1)Δ,xΔ],B=[T,∞))=
PT,n+1,y=P(C=[0,T]|A=[T,∞),
B=[(y-1)Δ,yΔ])=
PT,n+1,n+1=P(C=[0,T]|A=[T,∞),
B=[T,∞))=0
(8)
节点C在时间区间[T,∞)失效,则条件概率表分布式为
P(C=[T,∞)|A=[(x-1)Δ,xΔ],
B=[(y-1)Δ,yΔ])=1-PT,x,y
(9)
节点C在任务区间[0,T]内失效的条件概率表为如表1所示,同理也可得节点C在区间[T,∞)的CPT。
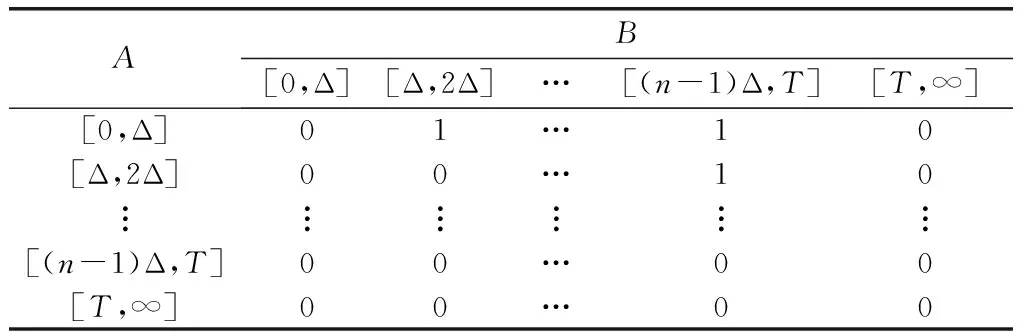
表1 优先与门节点C的CPT
2.1.2误差分析
在传统的BN转化方法下,优先门输出点C在任务区间[0,T]的失效概率Pc为
(10)
由表1可得,式(10)可转化为
(11)
设ta为A的失效点,tb为B的失效点,根据复合梯形积分方法可得优先与门的输出顶事件C在任务区间[0,T]的失效概率Pc1为
(12)
Pc1是优先与门的顶事件的失效概率的真值,则传统的BN转化方法的计算结果的误差ε1为ε1=|Pc-Pc1|。
其中可用将任务区间[0,T]分为n段的方法,对式(12)进行转化,则
(13)
由式(11)和式(13)得
(14)
利用夹逼定理可得
(15)
当n取值小时,传统贝叶斯转化方法的误差会很大;当n→∞时,误差变小并趋近于0。验证了当n取值越大时传统贝叶斯转化方法的精度越高,误差越小,同时可知当n越大时,计算时间变长,各个部件的CPT的规模变大。
2.1.3改良方法
根据前面得出的传统方法的计算误差和复合梯形积分方法,利用得到的误差直接修正节点C的CPT,改良优先与门的转化方法。改良方法在动态门中不存在重复事件的情况下完全补偿掉了计算误差,进而减小了存在重复事件情形下的动态门误差。
设定如果节点A和节点B在同一个时间区间[(x-1)Δ,xΔ]内失效时,节点C的失效概率不直接为0,即
PT,x=
P(C=[0,T]|A=[(x-1)Δ,xΔ],B=[(x-1)Δ,xΔ])=
(16)
特别对于服从指数分布的系统,即
(17)
则改良后节点C在任务区间[0,T]失效,条件概率表分布式为
PT,x,y=P(C=[0,T]|
A=[(x-1)Δ,xΔ],B=[(y-1)Δ,yΔ])=
(18)
改良节点C在任务区间[0,T]内失效的条件概率表如表2所示。

表2 改良后的优先与门节点C的CPT
对于动态门中不存在重复事件的情况,改良后的转化方法,在n值很小时能保证结果的正确性,即ε1=0。在动态门中存在重复事件时,会存在比传统方法更加微小的误差。
2.2 备份门转化分析
根据备份件在储备状态时能量消耗的不同,在备份门可分为冷备份门(cold spare gate,CSP)、温备份门(warm spare gate,WSP)和热备份门(hot spare gate,HSP)。当主件处于工作状态时,备份单元处于储备状态;当且仅当主件失效后,备份单元才进入工作状态。对于冷备份门,备份单元在进入工作状态前视为无能量耗损,即失效率为零。
2.2.1传统的备份门转化方法
由CSP性质可知,当且仅当主件失效后,备份单元才进入工作状态,备份单元在储备状态时失效率为零。CSP向DTBN转化如图2所示。

图2 冷备份转化为DTBN
当x Px,y=P(B=[(y-1)Δ,yΔ]|A=[(x-1)Δ,xΔ])= (19) 对于服从指数分布的系统,不妨设A的失效率为λa,B的失效率为λb,概率密度分别为:fA(t)=λae-λat,fB(t)=λbe-λbt,则 Px,n+1=P(B=[T,∞)|A=[(x-1)Δ,xΔ])= (20) B的条件概率分布式为 P(B=[(y-1)Δ,yΔ]|A=[(x-1)Δ,xΔ])= (21) P(B=[(y-1)Δ,yΔ]|A=[T,∞))=0 (22) P(B=[T,∞)|A=[T,∞))=1 (23) 节点B的CPT如表3所示。 表3 备份门节点B的CPT 节点C的条件概率分布式为 P(C=[(z-1)Δ,zΔ]|B=[(y-1)Δ,yΔ])= (24) 2.2.2误差分析 在传统转化方法下,优先门输出点C在任务区间[0,T]的失效概率Pc为 Pc=P(C=[0,T])= (25) 由表3可知,式(25)可转化为 (26) 设ta为A的失效点,tb为B的失效点,根据复合梯形积分方法可得冷备份门的节点C在任务区间[0,T]的失效概率Pc1为 (27) 则Pc1是CSP输出的失效概率真值,传统BN转化方法的计算结果误差ε2为 (28) 2.2.3改良方法 根据传统方法的计算误差和复合梯形积分方法,利用得到的误差直接修正节点B的CPT,改良备份门的转化方法。在以前方法的基础上,额外设定当x=y时,B的条件概率为 Pxx=P(B=[(x-1)Δ,xΔ]|A=[(x-1)Δ,xΔ])= (29) 特别地,对于服从指数分布的系统为 (30) 则改良后节点B在任务区间[0,T]的条件概率表分布式为 P(B=[(y-1)Δ,yΔ]|A=[(x-1)Δ,xΔ])= (31) 对于备份门中不存在重复事件的情况下,改良后的转化方法,在n值很小时能保证结果的正确性,即ε1=0。改良后的转化方法比传统方法拥有更高的计算精度。 以某测量系统为例,验证改良方法的可行性和高效性。测量系统的动态故障树模型如图3所示,其中M为密封胶,L、J是两个关键电子元器件,D为红外传感器,E为接口,F为备用接口。 图3 系统的动态故障树 不妨设定所有的部件在工作状态下都服从指数分布。设其分布参数为:λA=2×10-3h-1、λB=5×10-3h-1、λC=8×10-3h-1、λD=3×10-3h-1、λE=10-3h-1和λF=4×10-3h-1。将动态故障树转化为BN,代入相关数据进行分析计算。 使用Matlab软件分别计算传统DTBN方法和新的改良方法[17]。根据各个部件失效率的数量级,不妨设定工作时间T=1 000 h,两种方法的结果对比如表4所示。 表4 两种方法的失效概率与耗时 由表4可知,当n取值相同时,两种方法各个部件的CPT规模相同,改良方法的精度比传统方法的精度更高,误差更小。 对于所有部件服从指数分布的系统,使用马尔可夫方法计算得到系统的失效概率F(1 000)=0.557 203。可知改良方法可以有效并很快地得到系统的失效概率。在n很小时,改良方法就能得到系统失效概率的数量级。 蒙特卡罗仿真方法适用于服从任何分布类型的动态故障树分析,但其往往需要耗费大量的计算时间。运用蒙特卡罗方法对系统进行仿真的计算结果如表5所示。 表5 基于蒙特卡罗方法的系统失效概率与耗时 由表5可知,改良方法与蒙特卡罗方法相比,要得到同样的精度,前者耗时更短。 当n取值100时,运用马尔可夫方法、传统方法和改良方法得到系统可靠度如图4所示。 图4 基于3种方法的系统可靠度变化曲线 由图4可知,改良方法和马尔可夫方法的曲线误差区别极小,基本相互重叠,说明改良方法具有精度高、效率高等优点。 当部件L、E的失效分布服从两参数威布尔分布时,其分布参数分别为:mB=0.95、ηB=3×102h;mE=1.05、ηE=2×102h。部件M、J、D和F服从指数分布,λA=2×10-3h-1、λC=8×10-3h-1、λD=3×10-3h-1和λF=4×10-3h-1。使用Matlab软件,将动态故障树转化为BN,代入相关数据进行分析计算。设定工作时间T=1 000 h,两种方法的结果对比如表6所示。 表6 两种方法的失效概率与耗时 对于部件服从非指数分布的情形,运用蒙特卡罗方法对系统进行仿真的计算结果如表7所示。 表7 基于蒙特卡罗方法的系统失效概率与耗时 由表7可知,改良方法与蒙特卡罗方法相比,要得到失效概率的数量级,前者耗时更短。 分析计算了DTBN方法的计算误差,验证了当离散时间分段n的取值越大时,动态门的计算结果误差越小,但同时计算时间变长,节点CPT的规模变大。 针对传统方法的误差,提出改良方法补偿掉了传统方法的计算误差。改良方法拥有更高的计算精度和计算效率,解决了DTBN方法的计算时间、精度和效率受离散时间分段n极大影响的问题。在n很小时,改良方法就能得到系统失效概率的数量级。 通过某测量系统的实例分析,与马尔可夫方法和蒙特卡罗仿真方法进行对比,验证了改良方法的可行性。 改良方法继承了DTBN方法的优点,补偿了传统方法的误差,得到了更高的计算精度和计算效率。 参考文献: [1] DUGAN J B, BAVUSO S J, BOYD M A. Dynamic fault-tree for fault-tolerant computer systems[J]. IEEE Trans.on Reliability, 1992, 41(3): 363-376. [2] DUGAN J B, SULLIVAN K J, COPPIT D. Developing a low-cost high-quality software tool for dynamic fault-tree analysis[J]. IEEE Trans.on Reliability, 2000, 49(1): 49-59. [3] SMOTHERMAN M K, ZEMIUDEH K. A non-homogenedous Makrov model for phased-mission reliability analysis[J]. IEEE Trans.on Reliability, 1989, 38(5): 585-590. [4] DUGAN J B, Galileo: a tool for dynamic fault tree analysis[C]∥Proc.of the 11th International Conference on Computer Performance Evaluation: Modelling Techniques and Tools, 2000: 328-331. [5] AMARI S, DILL G, HOWALD E. A new approach to solve dynamic fault trees[C]∥Proc.of the Annual IEEE Reliability and Maintainability Symposium, 2003: 374-379. [6] AAMODT C A A, BANGS O, JENSEN F V, et al. Bayesian networks with applications in reliability analysis[J]. IEEE Trans.on Parallel & Distributed Systems, 2002, 22(3): 501-513. [7] LANGSETH H, PORTINALE L, LANGSETH H,et al. Applications of Bayesian networks in reliability analysis[J].Bayesian Network Technologies Applications & Graphical Models,2007. [8] SIMON C, WEBER P, EVSUKOFF A. Bayesian networks inference algorithm to implement dempster shafer theory in reliability analysis[J]. American Review of Respiratory Disease, 2008, 93(7): 950-963. [9] BOBBIO A, PORTINALE L, MINICHINO M, et al. Improving the analysis of dependable systems by mapping fault trees into Bayesian networks[J].Reliability Engineering & System Safety,2001,71(3): 249-260. [10] BOUDALI H, DUGAN J B. A new Bayesian network approach to solve dynamic fault trees[C]∥Proc.of the Reliability and Maintainability Symposium, 2005: 451-456. [11] BOUDALI H, DUGAN J B. A discrete-time Bayesian network reliability modeling and analysis framework[J]. Reliability Engineering and System Safety, 2005, 87(3): 337-349. [12] MONTANI S, PORTINALE L, BOBBIO A. Dynamic Bayesian networks for modeling advanced fault tree features in dependability analysis[C]∥Proc.of the ESREL, 2005:1414-1422. [13] MONTANI S, PORTINALE L, BOBBIO A, et al. A tool for automatically translating dynamic fault trees into dynamic Bayesian networks[C]∥Proc.of the Reliability & Maintainability Symposium Annual, 2006: 434-441. [14] NEIL M, TAILOR M, MARQUEZ D. Inference in hybrid Bayesian networks using dynamic discretization[J]. Statistics and Computing, 2007, 17(17): 219-233. [15] MARQUEZ D, NEIL M, FENTON N. Improved reliability modeling using Bayesian networks and dynamic discretization[J]. Reliability Engineering and System Safety,2010,95(4):412-425. [16] 周忠宝, 周经伦, 孙权, 等. 基于离散时间贝叶斯网络的动态故障树分析方法[J]. 西安交通大学学报, 2007, 41(6): 732-736. ZHOU Z B, ZHOU J L, SUN Q, et al. Dynamic fault tree analysis method based on discrete-time Bayesian networks[J]. Journal of Xi’an Jiaotong University, 2007, 41(6): 732-736. [17] MURPHY K P. The bayes net toolbox for Matlab[J]. Computing Science and Statistics,2001,33(2):1024-1034.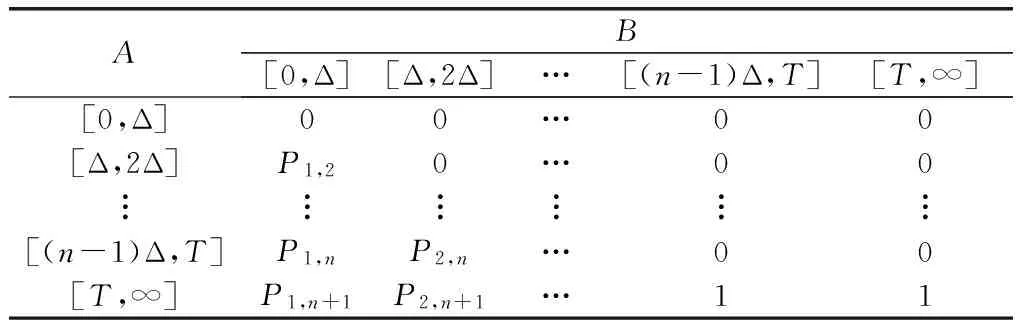
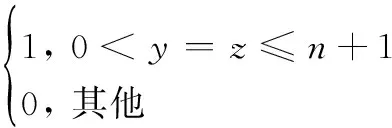
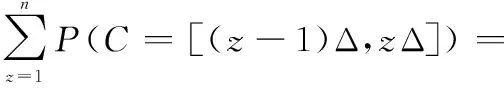

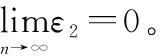
3 实例分析

3.1 指数分布情形



3.2 非指数分布情形


4 结 论

