缩径管内两相流砂粒碰撞和冲蚀特性研究

姚利明　刘巨保　张宏岩　张晓川　岳欠杯

1.东北石油大学机械科学与工程学院，大庆，1630002.大庆油田有限责任公司采油工程研究院，大庆，163000

0　引言

压裂施工时，流体携带固相颗粒高速撞击工具壁面，导致阀芯、压裂工具冲蚀破坏[1]，影响了工具使用寿命;而水力喷砂射孔[2]、射流除锈和表面光整加工等技术又利用冲蚀提高了工作效率和加工精度。上述工程实例均是通过流体输运颗粒，颗粒影响流体流动，从而改变颗粒对结构表面的作用力及冲蚀磨损量[3]。因此，分析高浓度液固两相流中，固相颗粒在冲蚀靶体附近的运动规律，特别是对颗粒间碰撞规律、颗粒与壁面作用力及材料冲蚀进行量化分析，有较大实际意义。

人们对工具冲蚀磨损、表面光整加工等进行了深入研究。王国荣等[4]研究了砂粒入射角对40Cr钢冲蚀量的影响，发现砂粒入射角由15°增大到90°时，冲蚀速率先增大后减小。王光存等[5]实验研究了氧化铝微粒对FV520B材料冲蚀影响，发现微粒质量在5～80 g之间时，冲蚀率先增大后减小，再趋于平稳。樊晶明等[6]采用微粒空气射流实验，研究了影响平板玻璃加工的因素，发现喷射距离对材料冲蚀率和冲蚀凹坑尺寸影响最大。XU等[7]采用软球模型考虑多颗粒间接触碰撞，研究了弯管内气固两相流对壁面冲蚀的影响，发现颗粒浓度对弯管冲蚀率影响显著。此外，颗粒浓度对冲蚀表面粗糙度影响很大，浓度越大材料去除越多，但粗糙度也越大[8]。实验研究发现，两相流黏度降低到一定值时材料冲蚀率将趋于稳定[9-10]。

综上，人们分析了固相颗粒质量、浓度、入射角度、射流距离和流体黏度等因素对冲蚀磨损的影响，但考虑两相流在冲蚀靶体附近发生的颗粒碰撞和堆积，研究流体黏度、砂粒浓度对颗粒与壁面作用力及材料冲蚀量的影响，还少有报道。因此，本文采用CFD-DEM方法建立缩径管两相流模型，通过实验验证了数值模型的准确性，分析了缩径管内砂粒的运动规律及其对两相流流态的影响，得出砂比和黏度对冲蚀量的影响规律。

1　固液两相流理论模型与实验平台

1.1　理论方法

1.1.1两相流理论

液固两相流流动过程中，固相颗粒受到来自液体作用力、颗粒间和颗粒与壁面间碰撞力，大量颗粒的存在会使液相的流动特性发生改变，对这一过程实现精细描述涉及液相与固相耦合作用。本文采用计算流体力学和离散单元耦合方法(computational fluid dynamics and discrete element method，CFD-DEM)对液固两相流进行描述，如图1所示，其中液相采用欧拉多相流模型求解[11-12]，固相颗粒采用离散单元法求解。液相和固相间相互作用主要通过曳力Fd以及网格单元中液相体积分数αl考虑，以实现图1a所示的网格单元间液相质量及液固两相动量的交换。

欧拉多相流模型假设网格中液相和固相同时占据空间，需采用在图1b所示的边界盒内抽取样本点的方法计算液相体积分数αl。首先将每个颗粒用边界盒包围，并在每个边界盒内规则地抽取样本点，如果样本点位于颗粒i内部，则将其保存为有效样本点数Nik；最后，对颗粒i的有效样本点数Nik进行检验，如果样本点位于网格单元k内，则将其保存为nik。因此，液相网格单元k内的固体颗粒体积为

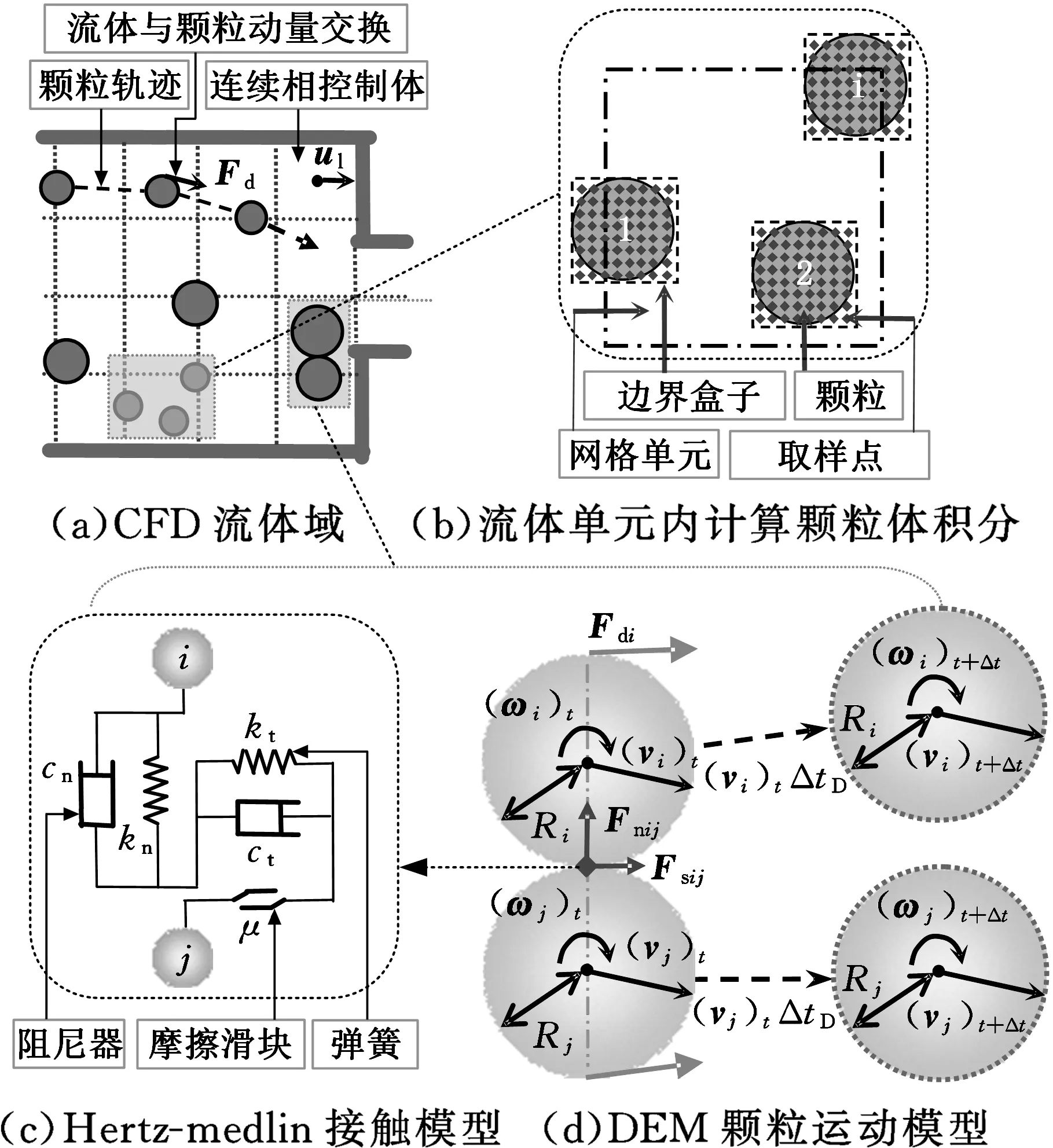
图1　CFD-EDM耦合方法理论Fig.1　CFD-DEM coupling method theory

式中，Vsi为颗粒i体积；z为网格单元k内颗粒数。

网格单元k固相体积分数为

(1)

式中，Vg为网格单元体积；αl为液相体积分数。

欧拉多相流模型的液相控制方程为

(2)

(3)

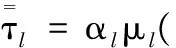
kls为液固相间的动量交换系数,可由下式求得[13]：

(4)

χ=3.7-0.65exp[-(1.5-lgRes)2/2]

Res=(2αlρlRs|ul-us|)/μl

式中，Fd为液相与颗粒间曳力；Cd为曳力系数；Res为颗粒雷诺数；Rs为颗粒半径。

本文算例中，由于液相速度高且固壁附近存在速度梯度，故主要考虑颗粒受到的重力、浮力、曳力、升力和碰撞接触力。颗粒形状假设为球型，据图1d所示的颗粒受力情况可得固相任一颗粒动力学控制方程：

(5)

(6)

式中，ms为颗粒质量；ωs和Is分别为颗粒角速度及转动惯量；Fs和Ts分别为颗粒碰撞过程接触力和力矩。

颗粒间接触碰撞过程通过图1c所示软球模型描述，即在颗粒i和j间设定了弹簧、阻尼器、滑动器和耦合器对颗粒接触过程进行模拟。接触力可分解为法向接触力和切向接触力，法向接触力为

Fnij=(-knα3/2-cnusij·nnij)nnij

(7)

式中，下标ij为颗粒i与颗粒j间的物理量；α为法向重叠量；nn为颗粒间法向单位矢量；kn和cn分别为颗粒法向刚度和法向阻尼系数。

切向接触力表示为

Ftij=-ktδ-ctustij

(8)

式中，kt和ct分别为颗粒切向刚度和切向阻尼系数；ust为接触点滑移速度；δ为接触点切向位移。

若接触点发生滑动，则颗粒的切向力为

Ftij=-μs|Fnij|ntij

式中，μs为静摩擦因数；nt为颗粒间切向单位矢量。

颗粒浓度较高时，颗粒i可能同时与m个颗粒接触，作用在颗粒i的总力和总力矩为

(9)

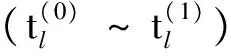
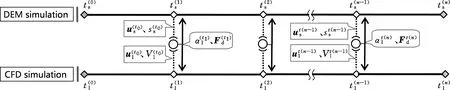
图2　CFD-DEM耦合方法求解过程Fig.2　CFD-DEM coupling method solving process

1.1.2冲蚀理论

冲蚀量计算采用Archard基于接触力学提出的磨损方程[14-15]，即

(10)

S=vt

式中，V为冲蚀体积，m3；S为冲蚀深度，m；W为冲击载荷，N；σs为材料屈服极限，Pa；K为与材料属性相关的冲蚀常数；v为冲蚀速度，m/s；t为冲蚀时间，s。

1.2　数值模型

缩径管结构如图3所示，初始条件下，缩径管内充满混砂液，模型主要结构及物性参数见表1。

图3　缩径管结构示意图Fig.3　Contraction pipe structure

表1　CFD-DEM耦合模型计算参数Tab.1　CFD-DEM coupling model calculation parameters

图4所示为模型网格及边界条件，模型左上端入口采用速度入口边界，右下端出口采用压力出口边界，其余均为壁面边界。因流体计算对壁面网格尺寸要求较高，故对壁面附近网格加密，并进行网格无关性验证，流体域共划分61 426个六面体网格单元。压力速度耦合使用压力关联方程的半隐式算法(Simple)，保证收敛率；压力离散插值方式采用标准方式(Standard)；湍流模型选取RNGk-ε模型，动量、湍动能以及湍流耗散率采用一阶迎风格式的有限体积法进行离散。

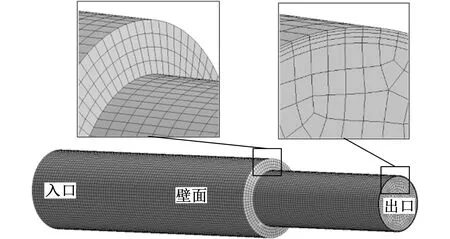
图4　缩径管流场网格模型及边界条件Fig.4　Contraction pipe flow field mesh model and boundary

1.3　实验平台

建立图5所示的高浓度固液两相流冲蚀测试平台，平台主要由水力循环系统和冲蚀测试段组成。水力循环系统包括压裂车组、输流管路和蓄水池。压裂车组选用油田大功率、大排量压裂施工常用车型，包括储砂车、储液车、混砂车、SS-2000型压裂泵车和压裂仪表车。冲蚀测试段可以更换冲蚀试件。

如图6所示，压裂仪表车是实验的指挥车，可协同控制储砂车、储液车、混砂车、压裂泵车进行冲蚀实验。实验员在压裂仪表车内，按设计将储液车内压裂液和储砂车内石英砂调入混砂车，得到混砂液。而后混砂液在压裂泵车抽吸、加压作用下，注入冲蚀测试段，进行冲蚀实验；同时，压裂仪表车具备数据采集和实时监测功能，可调取压裂泵车的流量数据和混砂车的砂比数据，实时将流量和砂比等数据显示在监测屏上，供实验员参考和记录。

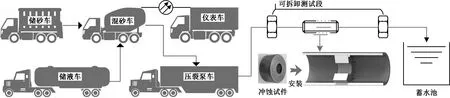
图5　实验装置示意图Fig.5　Schematic of experimental installation

图6　实验装置实物Fig.6　Pictures of experimental installation

2　实验条件及工况

2.1　压裂砂选择

按照石油天然气行业标准Q/SY125-2007《压裂支撑剂性能指标及测试推荐方法》，筛选确定直径0.4～0.9 mm优质石英砂作为本实验的压裂用砂。

2.2　压裂液设计

实验用改性胍胶压裂液配方同现场施工用压裂液配方相同，主要成分为0.8%稠化剂、0.2%表面活性剂、有机硼和适量清水，交联比为100∶1。参照石油天然气行业标准ST/Y 6376-2008《压裂液通用技术条件》，在30 ℃、170 s-1、剪切40 min条件下完成改性胍胶压裂液流变实验，确定表观黏度稳定在180 MPa·s。

2.3　计算工况

为分析高浓度固液两相流中砂比、流体黏度对缩径圆管冲蚀的影响，首先通过实验验证了本文数值方法的准确性，而后采用数值方法研究了砂比Sv、黏度μ对缩径管冲蚀的影响，具体参数见表2，实验和数值模型涉及的基本参数取值见表1。

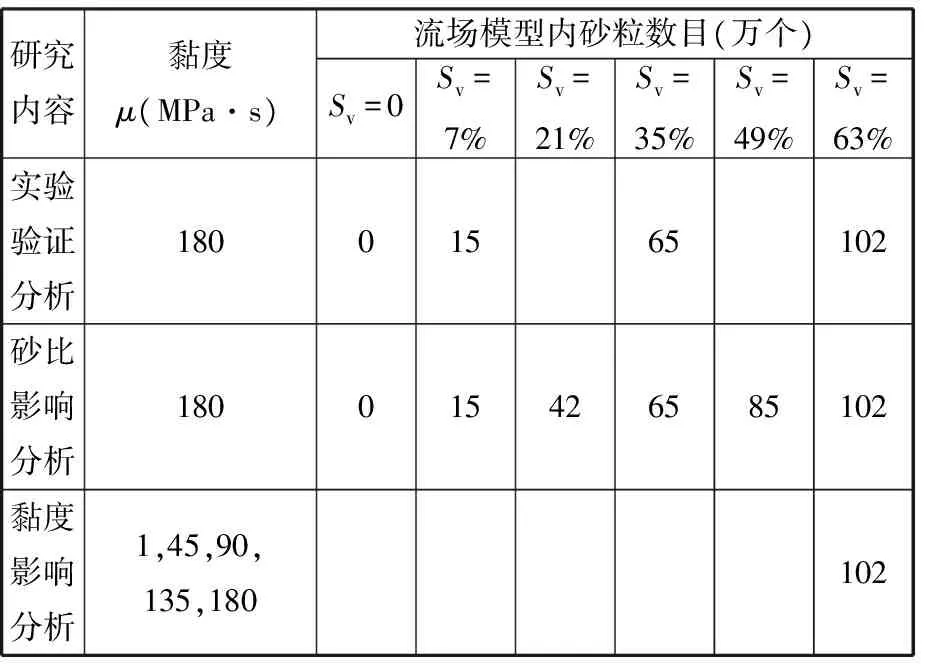
表2　相关参数和模型内砂粒数目Tab.2　Related parameters and numbers of sand grains in model

本文数值计算采用CFD-DEM方法，不同缩径管内径、砂比均对应模型内不同砂粒数目，计算方法如下。

设流体域内有砂体积Vvs(视体积)，水体积Vl，水砂混合后，砂在水中的体积为0.62Vvs(0.62为水砂混合系数，等于砂视体积密度ρvs除以砂实际密度ρs)。则混合液的体积为Vm=0.62Vvs+Vl，设混合液密度为ρ，则由质量守恒定律可得

ρ(0.62Vvs+Vl)=ρvsVvs+ρlVl

(11)

式中，ρl为液体密度。

又因砂比Sv=Vvs/Vl，结合式(11)可得砂质量为

Ms=ρvsVvs=ρvsVm(1/Sv+ρvs/ρs)-1

则颗粒个数为

Ns=Ms/ms

(12)

式中，ms为单颗粒质量。

由式(12)计算不同砂比的砂粒数目列入表2中，作为数值计算依据。

3　结果分析

3.1　冲蚀实验与数值模型对比验证

实验选取硬度较低、塑性较好的20钢作为冲蚀靶体材料，每个试件冲蚀15 min。冲蚀试件原结构如图7a所示，D=38 mm、d=12 mm，实验分析3种砂比(7%、35%、63%)，每种砂比3个试件，共实验9个试件；试件冲蚀后结构如图7b所示，因本文数值模型可得到冲蚀面的冲蚀深度，为便于实验与数值模拟对比分析，将试件径向宽度dn四等分，共得到d0、d1、d2、d3、d45个点，测量每点冲蚀的轴向投影高度(冲蚀深度)h0、h1、h2、h3、h4，测量数据取3个试件均值。实验和数值模拟的试件冲蚀情况如图8和图9所示，利用实验测量和数值计算得到冲蚀深度h来绘制图10所示冲蚀深度对比误差曲线。数值模拟计算得到的h2和h4位置冲蚀深度随时间变化规律见图11。

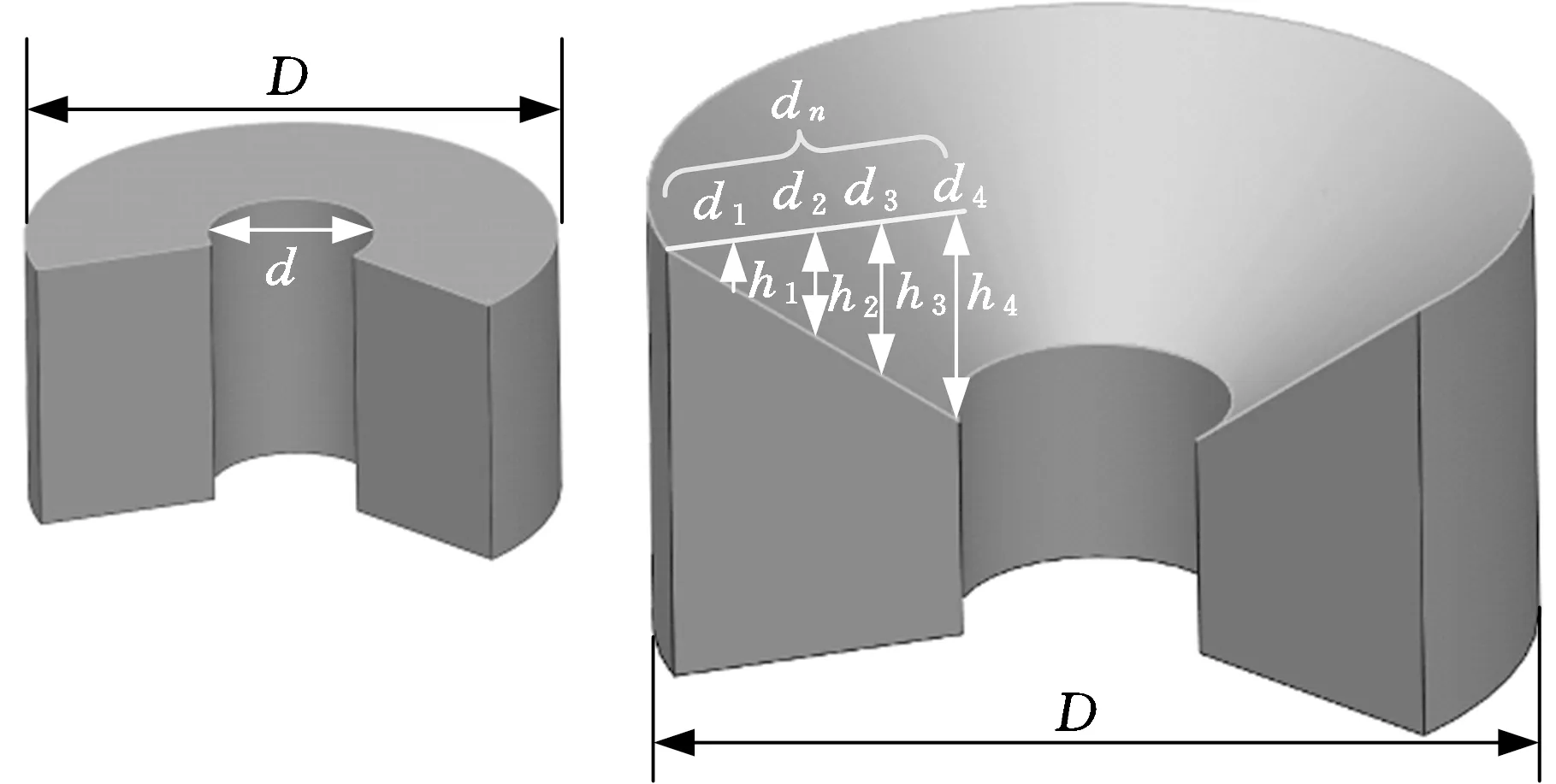
(a)原结构 　　 　　　　 (b)冲蚀后图7　冲蚀试件示意图Fig.7　Schematic of erosion specimen

(a)Sv=0 (b)Sv=7% (c)Sv=35% (d)Sv=63%图8　实验冲蚀结果Fig.8　Erosion results of experimente

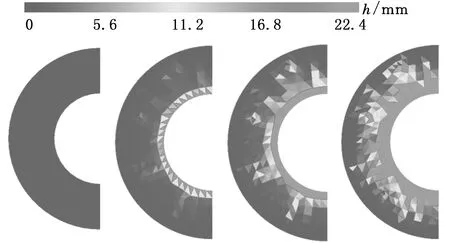
(a)Sv=0 (b)Sv=7% (c)Sv=35% (d)Sv=63%图9　数值模拟冲蚀结果Fig.9　Erosion results of numerical simulation

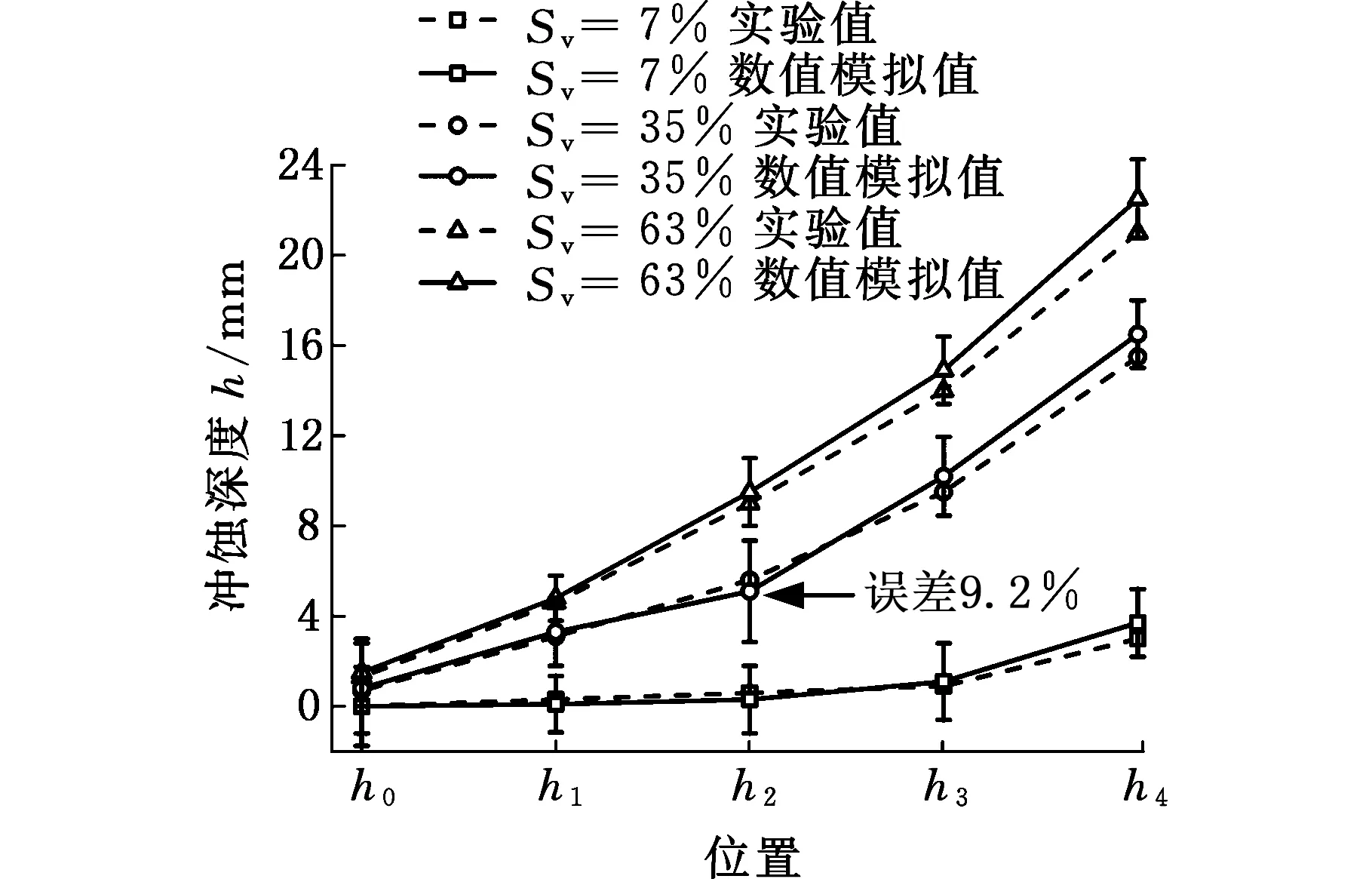
图10　实验与数值模拟冲蚀深度对比误差曲线Fig.10　Erosion contrast error curves of experiment and numerical simulation

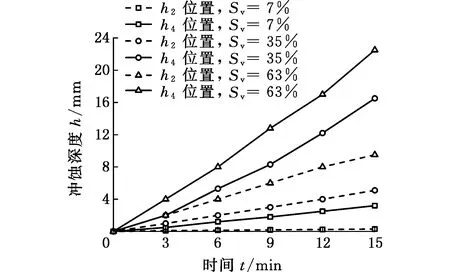
图11　冲蚀深度随时间变化曲线Fig.11　Curves of erosion depth changing with time

由图9所示缩径斜面冲蚀深度轴视图可见，斜面内缘比外缘冲蚀深度大；砂比越大，最大冲蚀深度越大，这与图8所示的实验结果吻合。文中Archard磨蚀方程可准确计算缩径斜面冲蚀深度，但仿真数据是在不考虑缩径斜面形变的假设条件下得到的，实际缩径斜面随冲蚀时间增加，表面形貌改变，冲蚀率不断变化。忽略斜面材料损失对冲蚀率的影响，对短时间预测是准确的，但对长时间冲蚀预测的结果误差会增大。文中冲蚀实验时间为15 min，且缩径斜面形变规则，由图10可知，实验与数值模拟冲蚀结果最大误差9.2%，则认为文中CFD-DEM耦合方法及Archard磨蚀方程可准确模拟高砂比的缩径管冲蚀规律。

由图11可知，随冲蚀时间的增加，冲蚀深度逐渐增大；相同冲蚀位置时，砂比越大，冲蚀深度越大；相同砂比时，斜面外缘h4位置比斜面内缘h2位置的冲蚀深度大。

3.2　砂比对缩径管壁面冲蚀影响机理分析

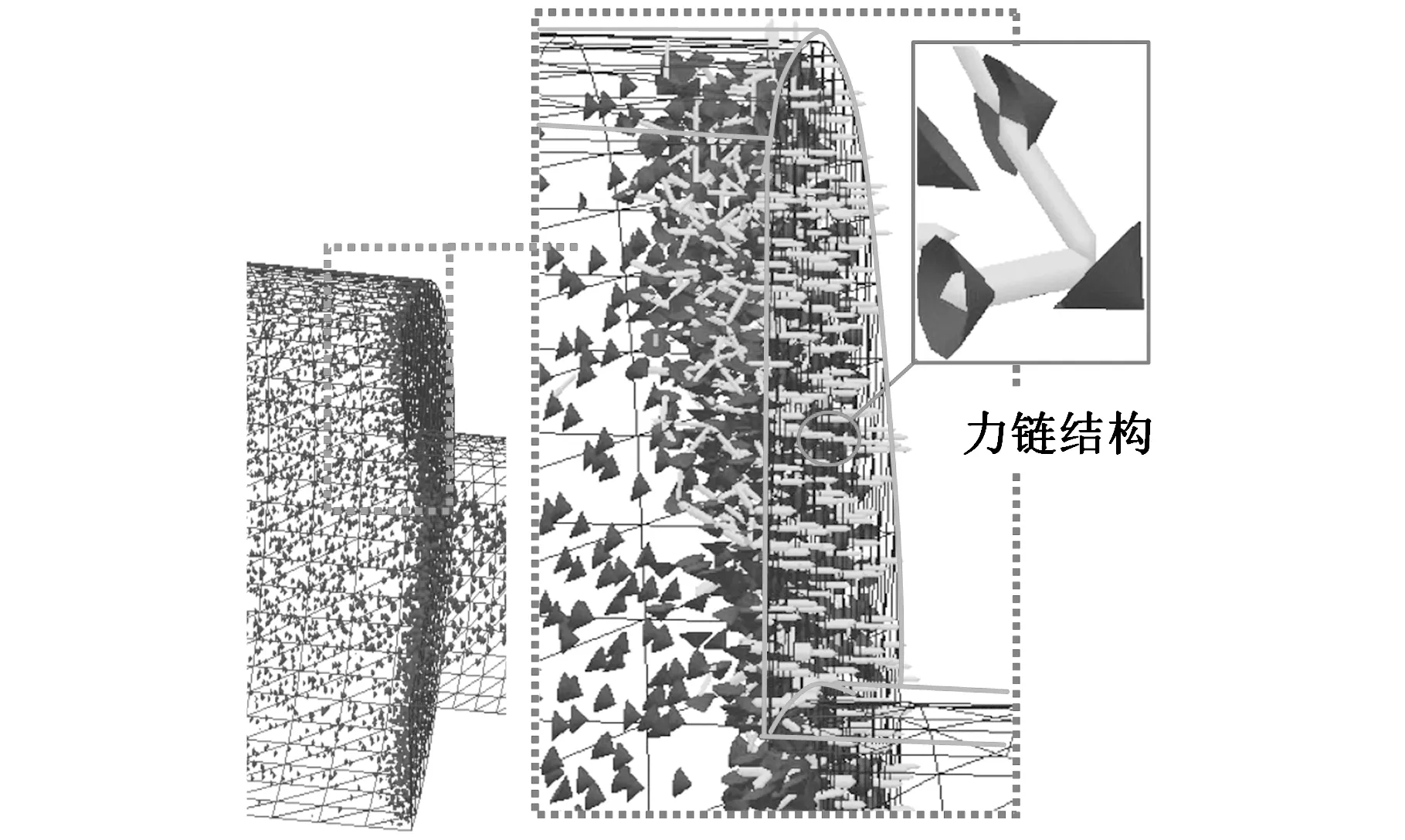
图12和图13给出了缩径管内两相流砂比分别为7%、35%、63%的砂粒间碰撞力分布和缩径斜面受到的颗粒碰撞力分布。图12中深色锥体表示砂粒，锥体尖端表示砂粒运动方向，浅色纺锤体表示砂粒间碰撞力。图14给出了两相流不同砂比的缩径斜面冲蚀深度曲线。

(a)Sv=7%

(b)Sv=35%

(c)Sv=63%图12　缩径管内砂粒接触力分布Fig.12　Contact force distributions of sand in contraction pipe

(a)Sv=7%

(b)Sv=35%

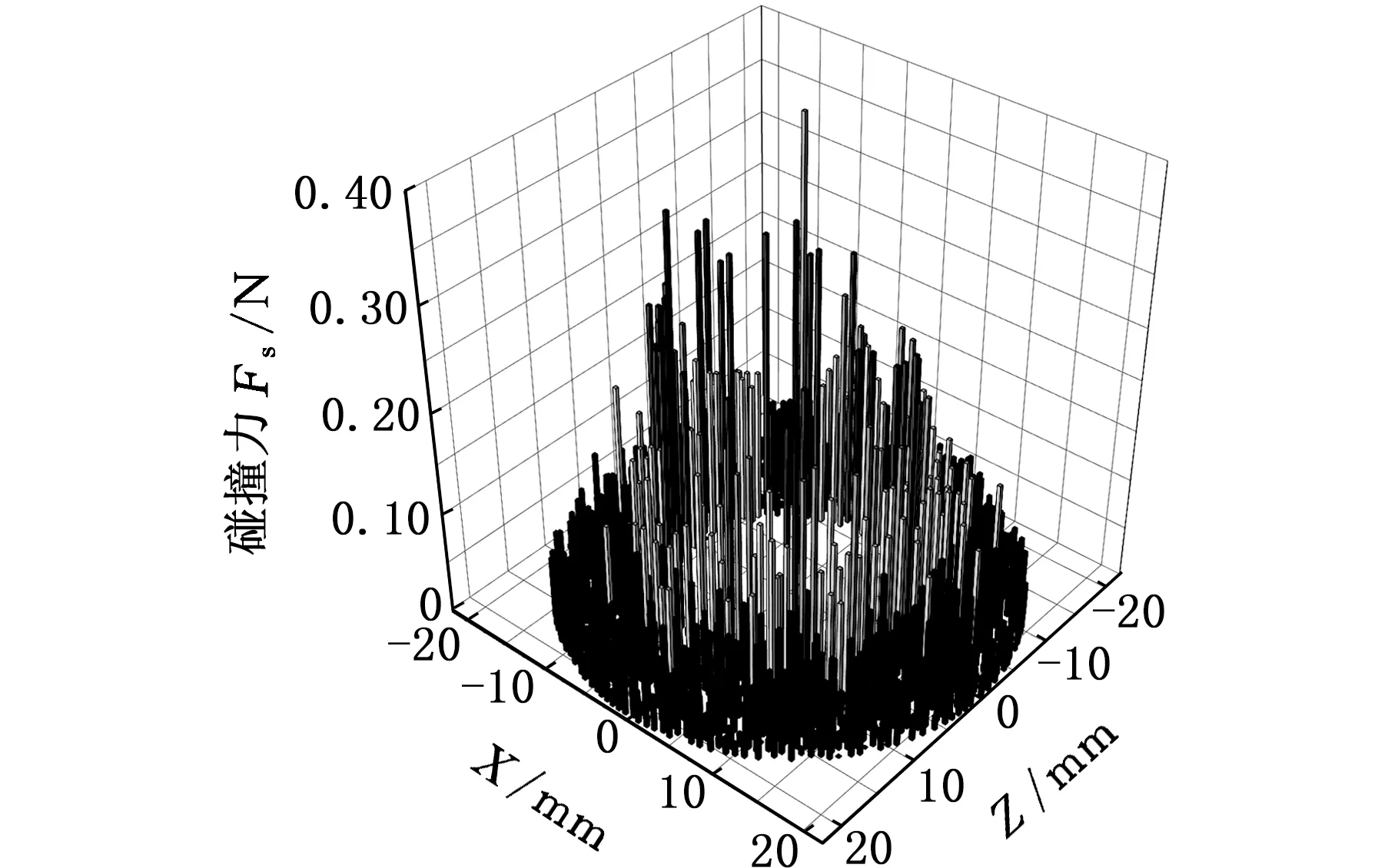
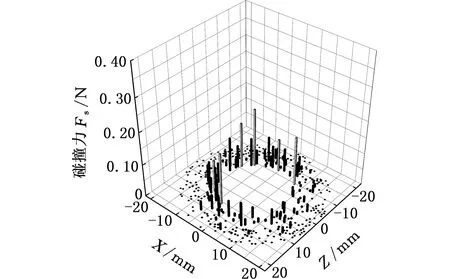
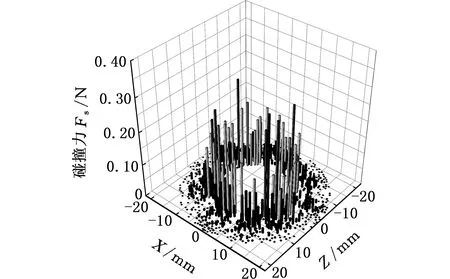
(c)Sv=63%图13　缩径斜面碰撞力分布Fig.13　Collision force distributions on contraction area

由图12可知，砂粒远离缩径斜面时，砂粒分布较均匀，砂粒间碰撞较少(浅色纺锤体少)，砂粒运动到缩径斜面附近时，砂粒间碰撞现象显著，多颗粒间碰撞并伴有碰撞力传递，形成图12a中的力链结构；砂比越高，缩径管内砂粒越密集，特别是缩径斜面附近由于砂粒间挤压、堆积作用显著，浅色纺锤体表示的砂粒碰撞力分布范围也越大。

图13给出了缩径斜面受到的砂粒碰撞力，每条立柱在XZ平面的投影表示砂粒与缩径斜面碰撞的落点，立柱的高度表示砂粒碰撞力大小。由图13a可知，从缩径斜面外缘向内缘方向，砂粒与壁面碰撞力增大，原因有两点：①缩径斜面外缘流场速度较内缘低，且方向急剧改变，颗粒易跟随流体运动，而缩径斜面内缘流场速度高，且方向基本沿管道轴向，则砂粒与斜面碰撞力大；②图12中缩径斜面外缘砂粒堆积显著，形成了堆积态砂粒保护层，阻碍了上游砂粒直接与缩径斜面发生碰撞，减小了砂粒与缩径斜面的碰撞力。

砂比增大，砂粒与斜面碰撞力增大，原因是单位时间、单位面积上的缩径斜面将承受更多的砂粒撞击，即使众多上游砂粒会因挤压、堆积不能与壁面发生直接碰撞，但碰撞力也会通过砂粒间挤压传递到壁面，增加了砂粒与壁面接触碰撞力。

由图14可知，砂比由0增至63%，砂粒与斜面碰撞力增大，斜面不同位置的冲蚀深度均增大。砂比由0增至40%的过程中，斜面不同位置的冲蚀深度增量较大，而砂比由40%增至63%过程中，斜面不同位置的冲蚀深度增量较小。也就是说，砂比与冲蚀深度的关系是非线性的，砂比大于40%时，相同时间的冲蚀深度增量明显减小，并趋于最大值。

图14　不同砂比的缩径斜面冲蚀深度Fig.14　Erosion depth of contraction area under different sand ratio

3.3　黏度对缩径管壁面冲蚀影响机理分析

图15和图16给出了缩径管内两相流黏度分别为1 MPa·s、90 MPa·s、180 MPa·s的砂粒间碰撞力分布和缩径斜面受到的颗粒碰撞力分布。图17给出了两相流不同黏度的缩径斜面冲蚀深度曲线。

由图15可知，流体黏度μ由1 MPa·s增至180 MPa·s时，流体对砂粒的夹携能力增大，缩径斜面上砂粒挤压、堆积现象减弱，斜面外缘附近接触力链分布范围减小，上游砂粒传递到斜面外缘的碰撞力也减小，因此，出现图16所示的流体黏度越大，砂粒在缩径斜面外缘产生的碰撞力越小的现象；又因流体黏度越大，流体黏滞力对砂粒碰撞的耗能越大，导致缩径斜面内缘碰撞力稍有减小。

(a)μ=1 MPa·s

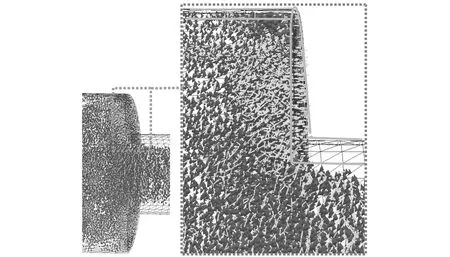
(b)μ=90 MPa·s

(c)μ=180 MPa·s图15　缩径管内砂粒接触力分布Fig.15　Contact force distributions of sand in contraction pipe

由前述分析可知，流体黏度越大，砂粒与缩径斜面的碰撞力越小，则缩径斜面的冲蚀深度越小，如图17所示。由图中数据可知，缩径斜面内缘的h4位置，在流体黏度为1 MPa·s时，斜面冲蚀深度达22.5 mm，流体黏度为180 MPa·s时，斜面冲蚀深度达19.4 mm，同比下降11%；缩径斜面外缘的h1位置，在流体黏度为1 MPa·s时，斜面冲蚀深度达5.1 mm，流体黏度为180 MPa·s时，斜面冲蚀深度达2.3 mm，同比下降56%。因此，流体黏度对缩径斜面外缘较对内缘的冲蚀深度影响大。

4　结论

(1)采用CFD-DEM方法建立了缩径管两相流模型，数值计算与实验测试冲蚀误差小于10%。分析发现，远离缩径斜面位置，砂粒分散均匀；靠近缩径斜面位置，砂粒堆积聚集，易形成力链结构。

(2)砂比越高，砂粒碰撞力分布范围也越大，从斜面外缘向内缘方向，砂粒与壁面碰撞力逐渐增大。缩径斜面冲蚀深度随砂比增大而增大，砂比大于40%时，相同时间冲蚀深度增量减小，并趋于最大值。

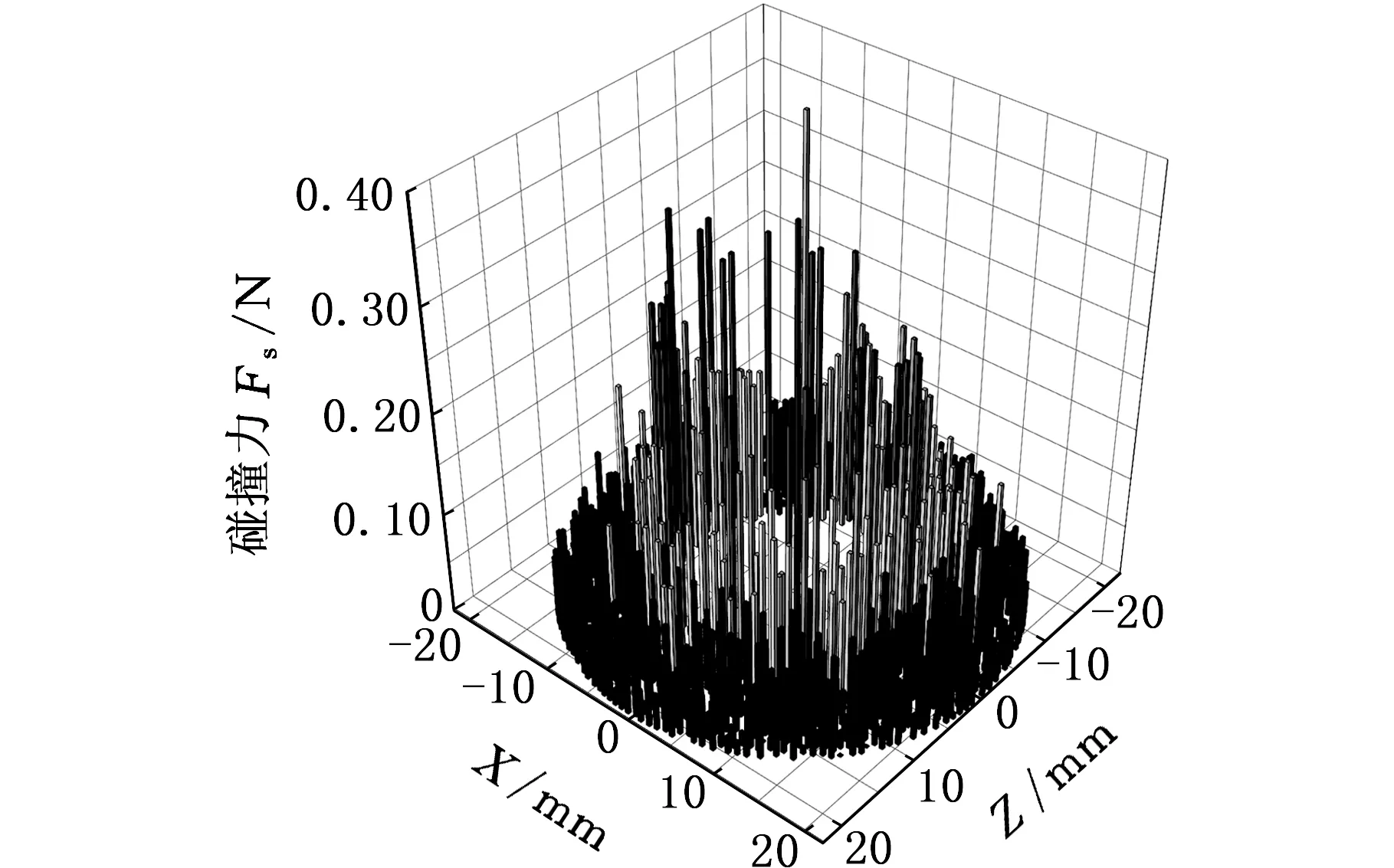
(a)μ=1 MPa·s

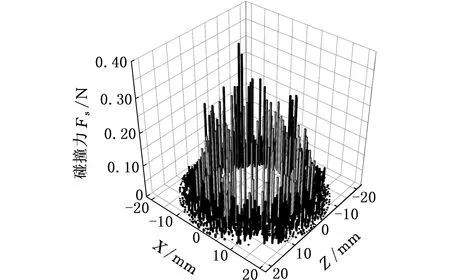
(b)μ=90 MPa·s

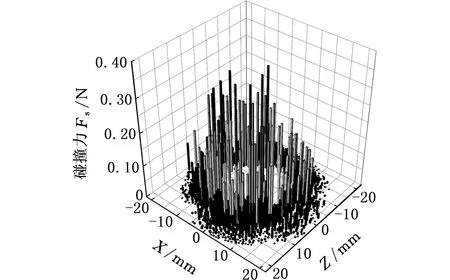
(c)μ=180 MPa·s图16　缩径斜面碰撞力分布Fig.16　Collision force distributions on contraction area

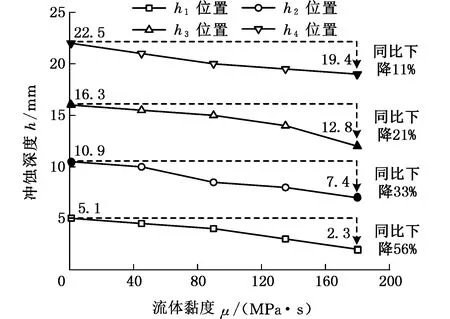
图17　不同黏度的缩径斜面冲蚀深度Fig.17　Erosion depth of contraction area under different viscosity

(3)流体黏度增大时，砂粒对缩径斜面产生的碰撞力减小，冲蚀深度减小；流体黏度对缩径斜面外缘的冲蚀深度影响比对内缘的冲蚀深度影响大。

参考文献：

[1]王川, 谢真强, 王国荣,等. 基于CFD的固井滑套冲蚀特性分析[J]. 机械设计, 2016(7):66-70.

WANG Chuan, XIE Zhenqiang, WANG Guorong, et al. Analysis of Erosion Characteristics of Cementing Liner Based on CFD[J]. Machine Design, 2016(7):66-70.

[2]高激飞, 胡寿根, 宁原林. 基于CFD的淹没磨料射流的数值模拟与流动特性研究[J]. 中国机械工程, 2003, 14(14):1188-1191.

GAO Jifei, HU Shougen, NING Yuanlin. Numerical Simulation and Flow Characteristics of Submerged Abrasive Jet Based on CFD[J]. China Mechanical Engineering, 2003, 14(14):1188-1191.

[3]薄纪康. 高压节流阀的冲蚀磨损机理及其激光熔覆再制造[J]. 中国机械工程, 2015, 26(2):255-259.

BO Jikang. Erosion Wear Mechanism of High Pressure Throttle Valve and Laser Cladding Remanufacturing[J]. China Mechanical Engineering, 2015, 26(2):255-259.

[4]王国荣, 钱权, 楚飞,等. 高压流体入射角对节流阀材料的冲蚀预测及验证[J]. 中国机械工程,2017,28(14):1652-1663.

WANG Guorong, QIAN Quan, CHU Fei, et al. Prediction and Verification of Erosion of Throttling Valve by High Pressure Fluid Incidence Angle[J]. China Mechanical Engineering, 2017，28(14): 1652-1663.

[5]王光存, 李剑峰, 贾秀杰,等. 离心压缩机叶轮材料FV520B冲蚀规律和机理的研究[J]. 机械工程学报, 2014, 50(19):182-190.

WANG Guangcun, LI Jianfeng, JIA Xiujie, et al. Study on Erosion Law and Mechanism of Material FV520B in Centrifugal Compressor Impeller[J]. China Mechanical Engineering, 2014, 50(19):182-190.

[6]樊晶明, 王成勇, 王军,等. 微磨料空气射流加工特性研究[J]. 中国机械工程, 2008, 19(5):584-589.

FAN Jingming, WANG Chengyong, WANG Jun, et al. Study on Machining Characteristics of Micro Abrasive Air Jet[J]. China Mechanical Engineering, 2008, 19(5):584-589.

[7]XU L, ZHANG Q, ZHENG J, et al. Numerical Prediction of Erosion in Elbow Based on CFD-DEM Simulation[J]. Powder Technology, 2016, 302: 236-246.

[8]GORANA V K, JAIN V K, LAL G K. Experimental Investigation into Cutting Forces and Active Grain Density during Abrasive Flow Machining[J]. International Journal of Machine Tools & Manufacture, 2004(44)：201-211.

[9]WILLIAMS R E. Acoustic Emission Characteristics of Abrasive Flow Machining[J]. Journal of Manufacturing Science and Engineering, 1998，120(2): 264-271.

[10]KAMALK K, RAVIKUMAR N L, PIYUSHKUMAR B T, et al. Performance Evaluation and Rheological Characterization of Newly Developed Butyl Rubber Based Media for Abrasive Flow Machining Process[J]. Journal of Materials Processing Technology, 2009,209(4): 2212-2221.

[11]计时鸣, 翁晓星, 谭大鹏. 基于水平集方法二维模型的软性磨粒两相流流场特性分析方法[J]. 物理学报, 2012, 61(1): 31-37.

JI Shiming, WENG Xiaoxing, TAN Dapeng. Analysis of Flow Characteristics of a Soft Abrasive Two Phase Flow Field Based on the Two-dimensional Model of Level Set Method [J]. Acta Physica Sinica, 2012, 61(1): 31-37.

[12]SOCCOL R, PISCKE A C G, NORILER D, et al. Numerical Analysis of the Interphase Forces in Bubble Columns Using Euler-Euler Modelling Framework[J].The Canadian Journal of Chemical Engineering, 2015, 93(11): 2055-2069.

[13]FELICE R D. The Voidage Function for Fluid Particle Interaction Systems[J]. International Journal of Multiphase Flow, 1994, 20(1): 153-159.

[14]ARCHARD J F. Contact and Rubbing of Flat Surfaces[J]. Journal of Applied Physics, 1953, 24: 981-988.

[15]HU Y, WANG C, YANG R, et al. The Attenuation Model of Sliding Guides Wear Theory Based on Archard Wear Model[C]// IEEE International Conference on Mechatronics and Automation. Tianjin, 2014:1570-1574.

(编辑王旻玥)