用于粒子分离器的砂粒反弹特性实验研究

李洁琼，周 军，王锁芳

(1.上海航天设备制造总厂，上海 200245； 2. 南京航空航天大学 能源与动力学院，江苏 南京 210016)

0 引言

粒子分离器对直升机发动机的进气防护起着至关重要的作用，然而粒子分离器的形面较为复杂，其形面主要由砂粒与壁面的反弹性质决定，砂粒与壁面的碰撞所带来的能量损失及内部流场扰动均会影响IPS的性能。如今对砂粒与不同材料的IPS壁面反弹特性未有一个统一的标准，故对砂粒的反弹特性展开实验研究具有重要的实际意义。

国外较早开始研究砂粒反弹特性，文献[1-3]早在17世纪后期便提出了经典刚体理论，说明简单方式碰撞时的砂粒特性。该理论建立在推动力与动量关系的基础上，忽略了碰撞过程中的瞬态力与砂粒滑移的影响。为分析砂粒与壁面的碰撞，已有相当多的实验探究展开，为数值模拟提供了数据。文献[4-5]运用激光多普勒风速风向测定法，对细小的玻璃微珠与塑性和弹性材料的碰撞展开探究。采用2种实验台探索低速与高速碰撞。分析砂粒入射角度与入射速度对法向恢复系数的影响发现，入射角度对于砂粒与硬板和软板的碰撞的影响截然不同。文献[6-7]运用光纤探头测量砂粒的速度，通过玻璃微珠碰撞不同材料的平板，发现当入射角度很小时，法向反弹系数很小，且粗糙度对于法向反弹系数的影响很小；但是未研究砂粒单独碰撞平板。

国内对于砂粒反弹特性的机理研究较少，文献[8]设计并建立了测量砂粒侵蚀炭化层反弹系数的实验系统，应用直径为1.5 mm的砂粒从不同角度侵蚀炭化层，测得不同入射角时的法向及切向反弹系数。应用准牛顿优化算法，利用三次方多项式拟合实验数据，得到法向反弹系数和切向反弹系数。文献[9-10]理论研究了耗散砂粒动力学方法在流动问题中的应用，给出了耗散流体砂粒运动的控制方程组、边界条件、数值方法及随机数据统计方法等。用固壁砂粒层结合流体砂粒反弹运动的方法来处理固壁边界有滑移流动边界条件。

上述文献均是针对砂粒反弹特性展开实验研究，并采用了多种测速方法捕捉砂粒的运动轨迹，分析了壁面反弹系数的影响因素，但选取的实验工况种类较少，局限于几种壁面材料，未能很好地应用于粒子分离器结构设计中。因此，设计砂粒反弹实验系统，拓展实验工况，并将实验结果应用于粒子分离器的设计工作中具有重要意义。

本文建立了砂粒反弹实验台，采用斜撞击反弹模型研究砂粒反弹特性，分析对比不同材料、不同粒径碰撞下的反弹系数，并将其拟合成多项式，为数值模拟粒子分离器内砂粒运动提供了可靠详细的反弹系数，进而可精确地优化设计粒子分离器，提高粒子分离器的性能。

1 砂粒反弹模型

应用弹性理论中文献[11-12]建立的斜撞击反弹模型，理论分析球形颗粒与不同平板的反弹特性，了解砂粒在碰撞前后的受力、速度变化及能量变化。图1为砂粒反弹前后速度矢量的示意图。图中：vi为砂粒入射速度；vr为砂粒反弹速度；θi为砂粒入射角(入射速度与法线的夹角)；vti，vni分别为入射速度vi的切向及法向分量；vtr，vnr分别为反弹速度vr的切向及法向分量；ωr为碰撞反弹后角速度；θr为砂粒反射角。

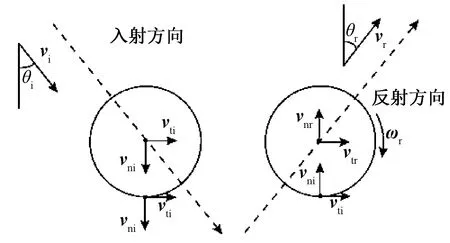
图1 砂粒速度矢量示意图Fig.1 Skematic diagram of particle velocity vector

有如下公式

(1)

(2)

vtr=Rωr

(3)

式中：vtr，vti，vnr，vni，vr，vi，ωr均为对应物理量的大小(下同)；R为砂粒半径；et为切向反弹系数；en为法向反弹系数。

定义I为砂粒碰撞时的冲量，f为切向与法向的冲量大小之比。

(4)

式中：In，It分别为法向和切向冲量；Fn，Ft分别为碰撞时砂粒受到壁面的法向和切向力。滑移存在时，满足

|Ft|=μ|Fn|

(5)

式中：μ为砂粒与固壁面之间的摩擦系数，μ=f。

动量定理(以法向与切向为正方向)为

In=m(vnr-vni)

(6)

It=m(vtr-vti)

(7)

动量矩定理为

Jα=∑M(Fi)

(8)

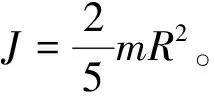
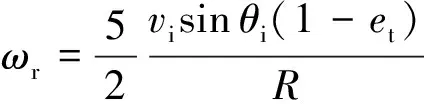
(9)

当砂粒与壁面发生碰撞发生滑移现象时，可得

et=1-μ(1+en)/tanθi

(10)

采用斜撞击反弹模型时，通过测量砂粒的入射速度vi、入射角θi、反弹速度vr、反射角θr，即可得出砂粒反弹特性的变化规律。

2 实验系统

图2为整个砂粒反弹实验系统的示意图，包括投砂系统、砂粒反弹实验箱、测试系统、砂尘回收系统等部分组成。

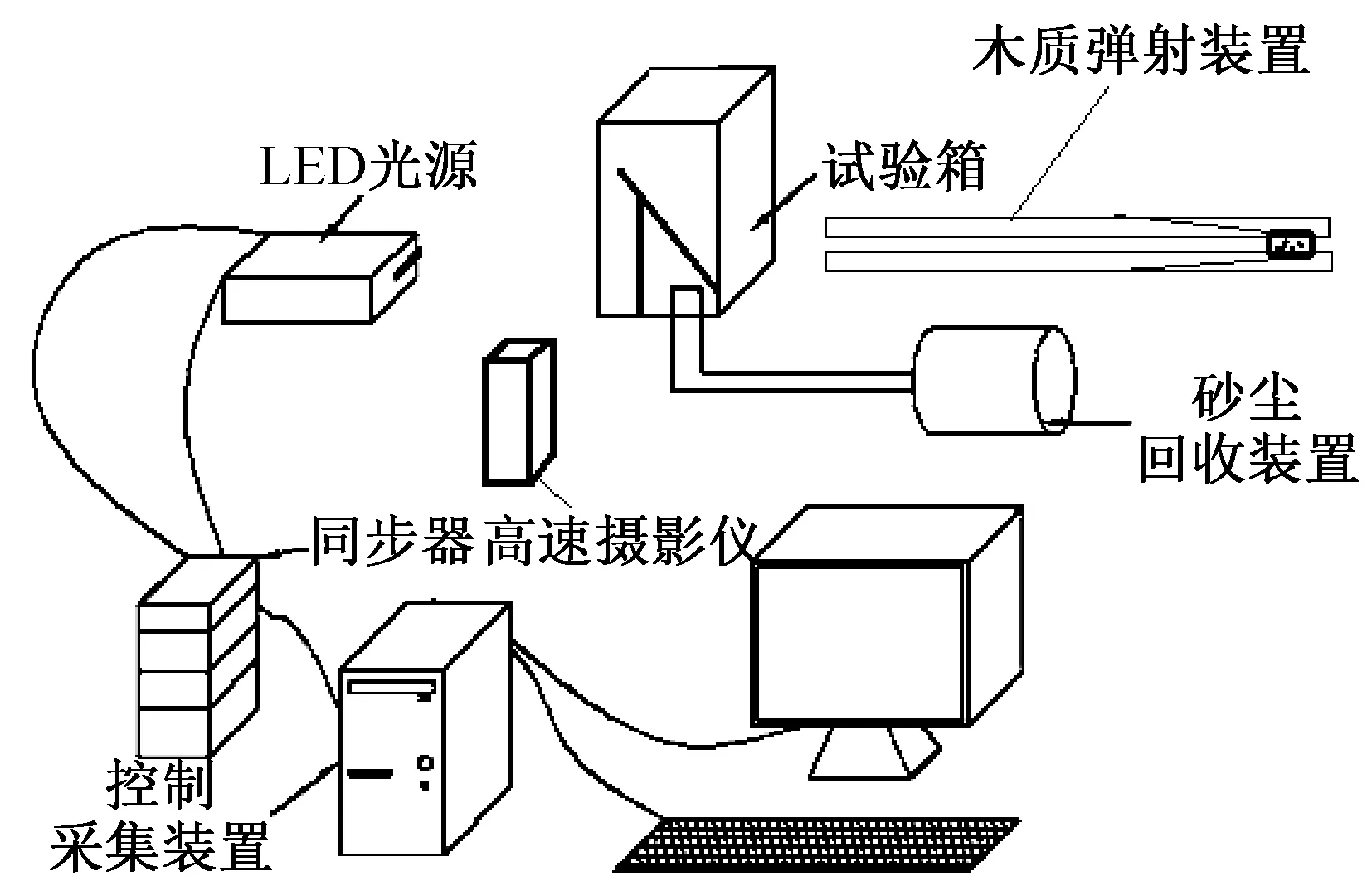
图2 砂粒反弹实验系统示意图Fig.2 Schematic diagram of experimental system of particle rebound

投砂系统主要由木质轨道、木质弹头以及弹性绳组成，其中弹头与皮带连接固定于轨道中，弹射原理是通过拉紧弹力绳使得装有砂粒的弹头具有一定的能量，松开弹力绳后弹头在轨道中快速运动并在出口处被阻拦，而砂粒则射入实验箱内，与实验板发生反弹。实验箱内包含碰撞平板、角度调节杆及安装架。通过调整调节杆与安装架，可改变平板的角度以及平板在实验箱内的位置。为保证拍摄效果的清晰度，将实验箱其中一个面喷上黑漆。同时为保证测试时具有良好的精度，拍摄部分换为光学玻璃。测试系统采用的高速摄影仪型号为Motion Pro Y5，镜头为Nikon 50 mm 1∶1.4D，最高拍摄速度为2 345 frame/s。调节高速摄影仪，将砂粒与实验板的碰撞前后的运动过程以单帧图片的形式储存于计算机中，通过软件处理得到砂粒反弹前后的速度矢量。

实验中采用树脂涂层、铝以及高温合金3种材料的实验板，通过调整3种材料的实验板与水平面的夹角，使得砂粒的入射角从 10°～90°均匀变化。实验物料分别采用粒径为350～500 μm的砂粒和粒径为580～800 μm的砂粒，且砂粒的入射速度保持20 m/s，且砂粒均采用球形颗粒，从而排除砂粒形状对壁面反弹系数的影响。

3 图像处理方法

调整高速摄影仪的拍摄速度至2 000 frame/s，待砂粒装入木质弹射装置中拉紧弹射装置中的皮带，这时高速摄影仪开始录制，直至砂粒与实验板碰撞后录制结束。图3为实验过程中其中一个砂粒的入射过程。图4为实验过程中其中一个砂粒的反射过程。

图3 砂粒入射图像Fig.3 Image of particle incident process

图4 砂粒反射图像Fig.4 Image of particle rebound process

图3、4中的图像叠加后即为砂粒的实际运动轨迹。其中每帧图像间隔时间为0.5 ms，量取相邻2幅图片中砂粒所走距离及与图像中白色标识的实际尺寸，比较可得砂粒的入射速度与反弹速度。测量图中砂粒轨迹与实验板角度，即可算出砂粒的法向与切向反弹系数。实验过程中，因砂粒与壁面碰撞的结果存在随机性，且砂粒的入射情况也是概率分布的，为减小实验误差，下文图中每个点代表保持入射速度与入射角度不变时，除去偏差较大的实验结果，统计20次实验结果的平均值。

4 实验数据分析

4.1 弹性碰撞下反弹系数的变化

因树脂材料板面弹性较好，砂粒与树脂壁面的碰撞为弹性碰撞。图5为砂粒与树脂板碰撞时的切向反弹系数随着入射角度的变化关系，其中横坐标为入射角度的弧度值。

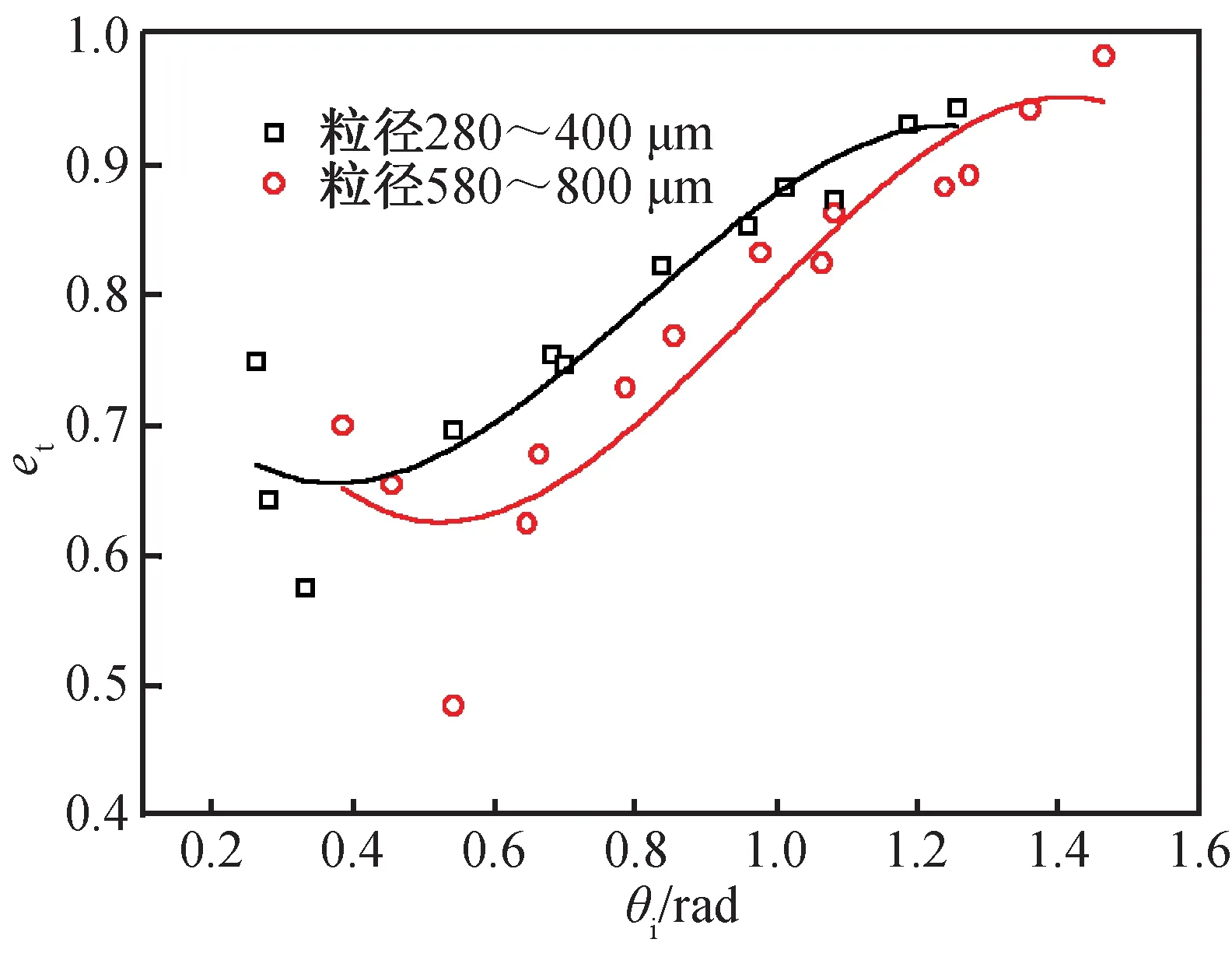
图5 弹性碰撞下切向反弹系数随着入射角度的变化Fig.5 Tangential restitution coefficient changing with incident angle under elastic collision

根据实验点的分布拟合成多项式曲线，由图5中拟合曲线可看出，对于弹性碰撞，壁面的切向反弹系数随着入射角度的增大而呈增大的趋势。 对于粒径为280～400 μm的砂粒，当入射角度为0.2 rad时，切向反弹系数接近于0.6，随着入射角度增大至1.4 rad时，切向反弹系数增大至0.9。当粒径为580～800 μm时，切向反弹系数随着入射角度的变化趋势虽与粒径较小时保持一致，但当入射角度较小或较大时，切向反弹系数的变化较为平缓，甚至趋于相反。其主要原因是：在入射速度不变的情况下，入射角度越小，与壁面的碰撞程度越强烈，因而能量消耗较大；切向反弹系数受砂粒滑移的影响，即与壁面的摩擦系数等特性有关，入射角度较小时，法向入射速度较大，产生的摩擦力较大，能量损失也较大。根据图中拟合曲线可得树脂材料的切向反弹系数的多项式为

ets(280-400)= 0.785+0.975αi-

1.89(αi)2+0.828(αi)3

(11)

ets(580-800)=0.918+0.458αi-

1.67(αi)2+0.924(αi)3

(12)

砂粒与树脂板碰撞时的法向反弹系数随着入射角度的变化关系如图6所示，横坐标为入射角度的弧度值，且图中每个点代表保持入射速度与入射角度不变的多次实验结果的平均值。

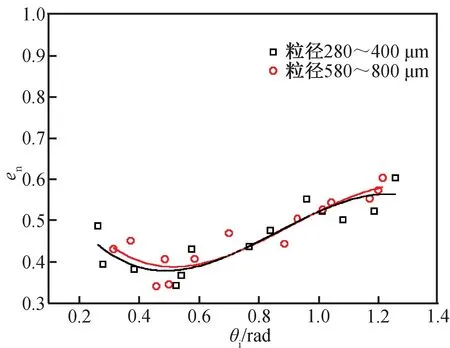
图6 弹性碰撞下法向反弹系数随着入射角度的变化Fig.6 Normal restitution coefficient changing with incident angle under elastic collision

从图6中可看出，对于粒径为280～400 μm的砂粒，随着入射角度由0.2 rad增大至1.3 rad，法向反弹系数由0.4平缓增大至0.6；而对于粒径为580～800 μm的砂粒，随着入射角度的增大，法向反弹系数的变化趋势相同。故对于树脂材料板，砂粒的法向反弹系数受到入射角度的影响较小。其原因是：因砂粒与树脂壁面的碰撞为弹性碰撞，即壁面变形消耗的能量很少，砂粒在碰撞时产生的旋转动能与平移动能消耗较多。根据图中拟合曲线可得树脂材料的法向反弹系数的多项式为

ens(280-400)= 0.41+1.008αi-

1.94(αi)2+0.91(αi)3

(13)

ens(580-800)= 0.499+0.71αi-

1.64(αi)2+0.826(αi)3

(14)

4.2 弹性碰撞下旋转角速度的变化关系

由式(9)可看出，砂粒入射时的旋转角速度随着砂粒的入射角度及切向反弹系数的变化而变化。图7为2种粒径的砂粒在弹性碰撞下的旋转角速度与入射角度的变化关系。横坐标为砂粒的入射角度，纵坐标为砂粒的旋转角速度。

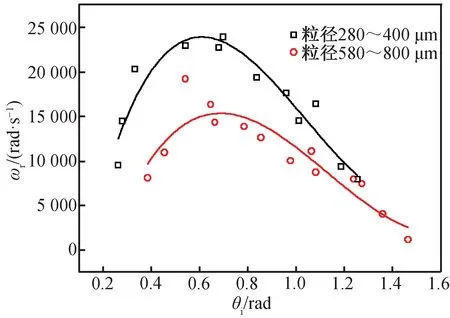
图7 弹性碰撞下旋转角速度随着入射角度的变化Fig.7 Rotation speed changing with incident angle under elastic collision

从图7中拟合曲线可看出，对于粒径为280～400 μm的砂粒，随着入射角度的增大，旋转角速度的变化平缓，且在入射角度达到25°时，砂粒的旋转速度达到最大；随着入射角度继续增大，旋转角速度随之缓慢减小。而对于粒径为580～800 μm的砂粒，则随着入射角的增大，旋转角速度先增大后减小，在入射角为35°时达到最大值。对比图中2条拟合曲线可知，粒径较小的砂粒的旋转角速度的变化较粒径较大的砂粒平缓，且当入射角大于65°时，2种粒径的旋转角速度差值逐渐增大。说明粒径不同，砂粒的旋转角速度受到入射角度的影响也不同。

4.3 非弹性碰撞下反弹系数的变化

铝板与合金钢板的硬度较大，不易产生弹塑性变形，故砂粒与铝板、合金刚板之间为非弹性碰撞。图8为砂粒与铝板、合金钢板碰撞时切向反弹系数随着入射角度的变化关系。横坐标为砂粒入射角度的弧度值，纵坐标为切向反弹系数，图中的实验点均为多次重复实验所取的平均值。

图8 非弹性碰撞下切向反弹系数随着入射角度的变化Fig.8 Tangential restitution coefficient changing with incident angle under plastic collision

从图8中可见，铝板在2种粒径的砂粒的碰撞下，其切向反弹系数随着砂粒入射角度的增大而增大。在入射角度相同的情况下，当粒径较小的砂粒碰撞铝板时，切向反弹系数较大。同时，当入射角度较小时，粒径对于壁面切向反弹系数的变化影响较小，随着入射角度的增大，小粒径的壁面法向反弹系数较大粒径明显增大，且增大的趋势也更为剧烈，由此可知，粒径越大的砂粒与壁面碰撞，旋转动能与壁面变形消耗的能量越多，反弹系数较小。根据图中拟合曲线可得铝板的切向反弹系数的多项式公式为

etl(280-400)= 0.413 68+2.098 93αi-

3.655 1(αi)2+1.597 88(αi)3

(15)

etl(580-800)= 0.863 13+0.381 21αi-

1.595 5(αi)2+0.896 23(αi)3

(16)

对于合金钢板，当入射角度为0.45 rad左右时，粒径为280～400 μm的砂粒碰撞时，切向反弹系数达到最小值为0.62，随着入射角度的增大至1.2 rad时，切向反弹系数达到最大值0.85；而对于粒径为580～800 μm的砂粒碰撞时，切向反弹系数达到最小值为0.52，且在入射角度为1.4 rad时达到最大值为0.95。即粒径较大的砂粒碰撞合金钢板时，切向反弹系数较粒径较小的砂粒碰撞要大。同时从图中可看出，非弹性碰撞下的切向反弹系数的变化趋势与弹性碰撞下切向反弹系数的变化趋势相似。根据图中拟合曲线可得合金钢板的切向反弹系数的多项式公式为

eth(280-400)=0.855 53+0.570 53αi-

1.637 9(αi)2+0.791 63(αi)3

(17)

eth(580-800)=0.908 43+0.490 43αi-

1.743 7(αi)2+0.943 4(αi)3

(18)

非弹性碰撞下法向反弹系数随着砂粒入射角度的变化关系如图9所示。其中横坐标为砂粒入射角度的弧度值，纵坐标为切向反弹系数，图中的实验点仍为多次重复实验所取的平均值。

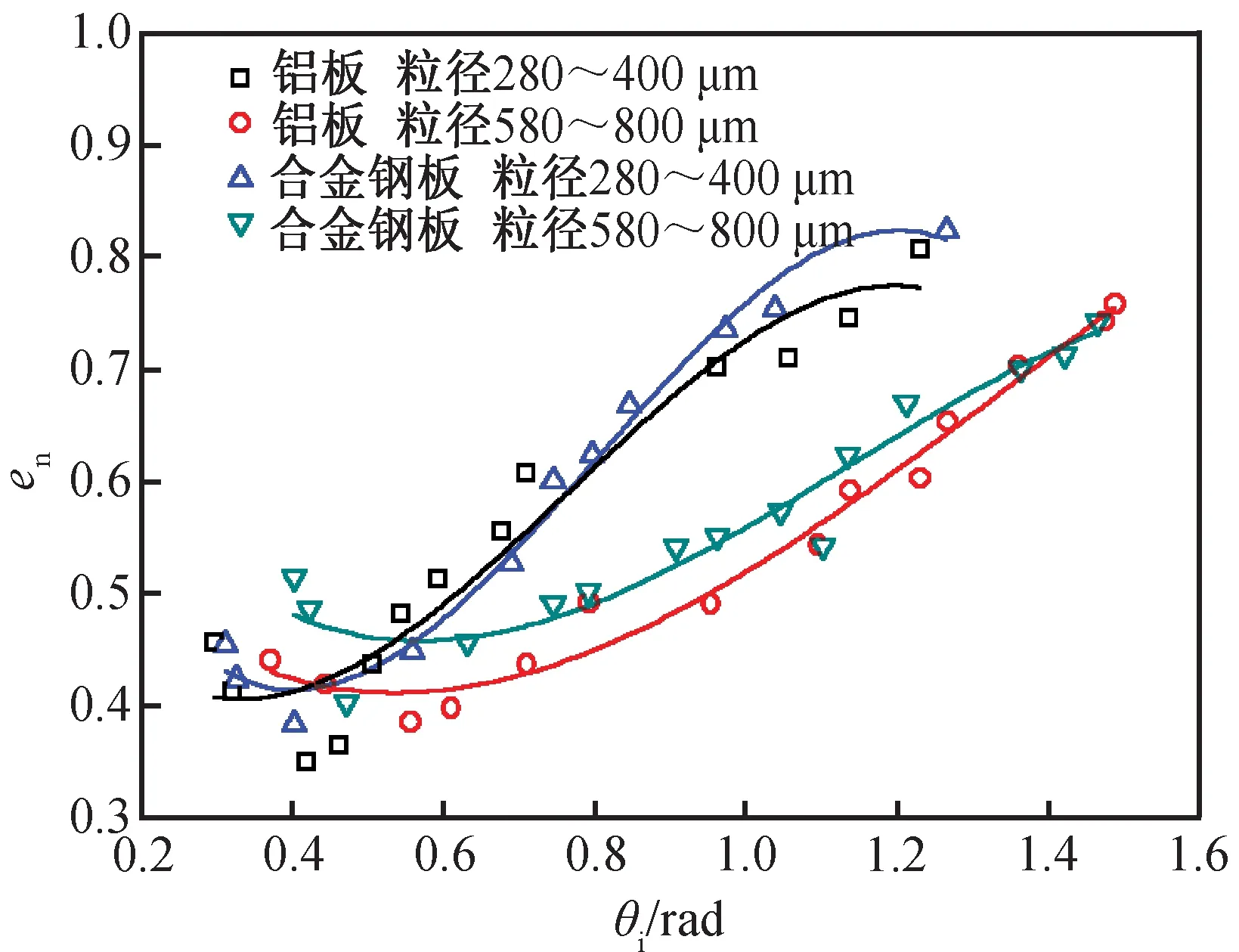
图9 非弹性碰撞下法向反弹系数随着入射角度的变化Fig.9 Normal restitution coefficient changing with incident under plastic collision

从图9可见，非弹性碰撞下法向反弹系数随着砂粒入射角度的变化与弹性碰撞下的变化不同，随着入射角度的增大，2种材料的法向反弹系数均随之增大。对于合金钢板较铝板，其法向反弹系数的变化更为平缓，说明非弹性变形起到一定的消耗作用。同时钢板表面因碰撞而产生的塑性变形(缺口、压痕等)也会影响到砂粒与板面的反弹特性。当入射角度较小时，粒径对于壁面法向反弹系数的变化影响较小，随着入射角度增大，小粒径的壁面法向反弹系数较大粒径明显增大，且增大的趋势也更为剧烈，由此可得，粒径越大的砂粒与壁面碰撞，旋转动能与壁面变形消耗的能量越多，反弹系数较小。根据图中拟合曲线可得2种材料的法向反弹系数的多项式公式为

enl(280-400)=0.508 81+1.582 84αi-

2.752 64(αi)2+1.136 5(αi)3

(19)

enl(580-800)=0.795 94-0.470 9αi-

0.167 4(αi)2+0.254 7(αi)3

(20)

enh(280-400)=0.478 81+2.084 79(α)i-

3.704 31(αi)2+1.602 85(αi)3

(21)

enh(580-800)=0.757 84-0.161 74αi-

0.573 89(αi)2+0.435 7(αi)3

(22)

4.4 非弹性碰撞下旋转角速度的变化关系

因砂粒碰撞时的角速度与切向反弹系数有关，故板面的硬度对砂粒的角速度也有影响。图10为非弹性碰撞下砂粒碰撞时的角速度与入射角度的关系。其中横坐标为砂粒的入射速度，纵坐标为砂粒的旋转角速度。

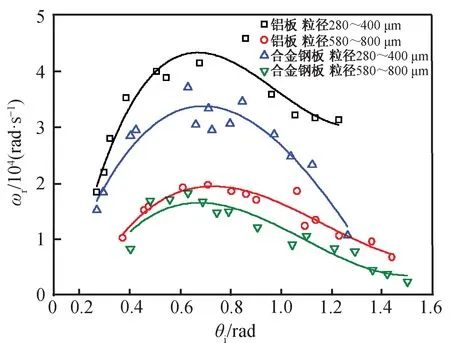
图10 非弹性碰撞下旋转角速度随着入射角度的变化Fig.10 Rotation speed changing with incident angle under plastic collision

从图10中可见，当砂粒粒径较小时，砂粒的角速度随着入射角度的变化较为剧烈，均呈先增大后减小的趋势；而对于粒径较大的砂粒，砂粒的旋转角速度随着入射角度的变化较为平缓，且较粒径较小的砂粒的旋转角速度平均减小20.22%。在铝板与合金钢板碰撞下，砂粒角速度较为接近，但当砂粒的入射角度为35°时， 与合金钢板碰撞的砂粒的旋转角速度达到最大值，而与铝板碰撞的砂粒在入射角度为55°时才达到最大值。与图7比较可知，因2种材料碰撞下的切向反弹系数较为接近，故对于非弹性碰撞，砂粒的旋转角速度受砂粒粒径的影响较大，受板面材料的影响相对较小。

5 结论

基于自行搭建的砂粒反弹特性测试实验台，采用2种粒径的砂粒碰撞3种不同材料的实验板，利用高速摄影仪测量砂粒的运动轨迹及运动参数，通过对比不同材料与不同粒径下反弹系数的变化来分析砂粒反弹特性的影响因素，实验结果表明：

1) 弹性碰撞下，壁面的切向反弹系数随着入射角度的增大而增大。当入射角度不变时，粒径为280～400 μm的砂粒碰撞时较粒径为580～800 μm的砂粒碰撞，切向反弹系数大。壁面的法向反弹系数随着入射角度的增大而变化平缓。入射角度不变时，粒径较小的砂粒碰撞时与粒径较大的砂粒碰撞时的法向反弹系数接近。

2) 弹性碰撞下，粒径为280～400 μm的砂粒的角速度随着入射角度的增大，先增大后减小，且在入射角度为0.6 rad时达到最大值；粒径为580～800 μm的砂粒的角速度随着入射角度的增大，先增大后缓慢减小，且在入射角度为0.7 rad时达到最大值。

3) 非弹性碰撞时，铝板与合金钢板在2种粒径的砂粒的碰撞下，其切向反弹系数随着砂粒入射角度的增大而增大，且粒径较大的砂粒碰撞合金钢板时，切向反弹系数大于粒径较小的砂粒碰撞时的切向反弹系数。相同粒径的砂粒碰撞时，合金钢板的切向反弹系数大于铝板的切向反弹系数。

4) 非弹性碰撞下法向反弹系数随着砂粒入射角度的变化与弹性碰撞下的变化相似，随着入射角度的增大，2种材料的法向反弹系数均随之增大。当入射角度较小时，粒径对于壁面法向反弹系数的变化影响较小，随着入射角度增大，小粒径的壁面法向反弹系数较大粒径的壁面法向反弹系数明显增大。

5) 当砂粒粒径较小时，砂粒的角速度随着入射角度的变化较为剧烈，均呈先增大后减小的趋势；而对于粒径较大的砂粒，砂粒的旋转角速度随着入射角度的变化较为平缓。粒径相同的砂粒碰撞铝板与合金钢板时，砂粒角速度较为接近，但当砂粒的入射角度为0.7 rad时，铝板与合金钢板碰撞的砂粒的旋转角速度达到最大值。

目前，对于不同粒径的砂粒与不同材料的粒子分离器壁面的反弹特性，国内外一直未有通用的模型和参数，不同壁面因反弹系数不同，砂粒运动存在差异性，对粒子分离器型面的影响不同，是粒子分离器设计的瓶颈。为此，设计了砂粒反弹实验系统，研究了砂粒的反弹特性，但未研究较小粒径的砂粒。后续的工作需采用更高拍摄速度的高速摄影仪获取砂粒的运动轨迹，研究砂粒的形状、材料等参数对于砂粒反弹特性的影响，进一步探索实验板的硬度、杨氏模量等参数对于反弹系数的影响。

[1] GOLDSMITH W, FRASIER J T. Impact: the theory and physical behavior of colliding solids [J]. Journal of Applied Mechanics, 1961, 28(4): 631-639.

[2] STRONGE W J. Rigid body collisions with friction[C]//Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. The Royal Society, 1990: 169-181.

[3] STRONGE W J. Impact mechanics[M]. England: Cambridge University Press, 2004.

[4] MARTIN S R， PINFOLD T M，WALLACE S G R.Applications of laser techniques to fluid mechanics[M].Berlin:Springer, 1991：125-141.

[5] SOMMERFELD M, HUBER N. Experimental analysis and modelling of particle-wall collisions [J]. International Journal of Multiphase Flow, 1999, 25(6): 1457-1489.

[6] FRANK T, SCHADE K P, PETRAK D. Numerical simulation and experimental investigation of a gas-solid two-phase flow in a horizontal channel [J]. International Journal of Multiphase Flow, 1993, 19(1): 187-198.

[7] LUN C K K, LIU H S. Numerical simulation of dilute turbulent gas-solid flows in horizontal channels[J]. International Journal of Multiphase Flow, 1997, 23(3): 575-605.

[8] 徐义华, 张燕海, 杨玉新, 等. 粒子侵蚀模型及砂粒侵蚀下绝热材料烧蚀数值计算[J]. 固体火箭技术, 2015, 38(1): 37-44.

[9] 孔轶华, 张楚华, 席光. 耗散粒子动力学在流动数值模拟中的应用[J]. 西安交通大学学报, 2006, 40(9): 1104-1108.

[10] 孔轶华, 张楚华, 席光, 等. 耗散粒子动力学对颗粒沉降问题的研究[J]. 工程热物理学报, 2008(1): 59-61.

[11] MAW N, BARBER J R, FAWCETT J N. The oblique impact of elastic spheres [J]. Wear, 1976, 38(1): 101-114.

[12] MAW N, BARBER J R, FAWCETT J N. The role of elastic tangential compliance in oblique impact [J]. Journal of Tribology, 1981, 103(1): 74-80.