基于数据挖掘的风电机组齿轮箱运行状态分析
贾子文 顾煜炯
华北电力大学能源动力与机械工程学院,北京,102206
0 引言
风电机组作为大型户外发电设备,受自然环境影响,其运行数据往往表现出非平稳性和结构非线性等特征[1]。同时,风电机组是一个复杂机械系统,为完成“风能-机械能-电能”的能量转化,机组各组成部分协同合作、相互影响,设备运行数据之间具有明显的关联性[2]。所以,如何从非平稳且存在复杂关联的运行数据中准确提取机组故障信息,及时发现并处理机组异常情况,对保证风电机组高效运行、降低风电运维开销、提高风电场经济效益起到至关重要的作用[3-4]。
为明确大型风力发电机组常见故障类型,对国内某风场1.5MW双馈风电机组2011年33台机组全年各部件故障率和发生故障造成的发电量损失进行调研。由统计结果发现,机组变桨系统、偏航系统、电气系统和控制系统的年故障率较高,但发电量损失较小。机组齿轮箱故障率虽然较低,但其引起的发电量损失所占比例最大。齿轮箱一旦出现故障,通常已到了故障的中晚期,需要租用大型起重设备进行吊装、更换等维修工作。相比其他故障,齿轮箱故障会产生更高的维修费用。同时,较长的停机时间,也严重影响机组的出力[5]。所以,实现对风电机组齿轮箱故障及时、准确的诊断,对保证风电机组稳定运行、提高风场效益十分关键。
目前,针对风电机组齿轮箱运行状态领域的问题,国内外专家学者已经进行了大量研究。文献[6]展开了对风电机组状态监测与健康管理关键问题的探讨,指出多源数据分析对机组状态监测与诊断的重要性。文献[7-8]建立了针对风电机组整机状态监测与分析的方法,运用数据采集与监视控制(supervisory control and data acquisition,SCADA)系统中的数据进行了机组运行状态分析。文献[9-11]分别利用神经网络、小波包和支持向量机的方法,对风电机组齿轮箱故障诊断问题进行研究,通过算法的改进提高了对齿轮箱故障类型的甄别能力。虽然以上方法对机组齿轮箱运行状态的分析均得到了较好的效果,但是这些研究大多缺乏对机组各运行数据之间、数据与机组运行工况之间相关性的分析,没有明确机组运行参数与运行状态之间的关联机制。机组一个确定的运行工况通常是由多个运行状态组成的,不同状态对机组运行参数的影响程度可能存在差异,所以,对机组数据之间、数据与运行状态的关联性研究是机组设备运行状态分析结果准确的重要保障。
针对这一情况,笔者对风电机组齿轮箱运行参数信息进行深度挖掘,通过极限学习机(extreme leaning machine,ELM)对非线性状态估计技术(nonlinear state estimate technology,NSET)进行合理改进,对齿轮箱各运行参数进行权重赋值,明确齿轮箱正常运行状态下各参数之间的相关性;运用因子分析,解析齿轮箱正常状态下不同动态过程对各类参数的影响程度,建立齿轮箱运行状态与参数特征间的关联机制,增强样本数据的解释能力;充分考虑风电机组实际运行情况,运用滑动窗口和异常率计算方法,减小数据波动和随机性,保证最终分析结果的准确性与可信性。
1 风电机组齿轮箱监测参数选取
齿轮箱作为双馈风电机组传动系统中的主要部件,完成转轴升速和转矩传递工作。为保证齿轮箱结构紧凑,齿轮箱采用一级行星-两级平行的结构,如图1所示,其中,低速级即齿轮箱输入端为行星轮系,低速轴输出与中速轴、中速轴与高速轴上的齿轮传动为常规斜齿轮传动。行星轮系中,太阳轮位于整个轮系的中心,通过3个行星轮与齿圈相联系,行星架、行星轮和主轴相连;中速轴、太阳轮输出轴和高速轴啮合;高速轴输出端通过联轴器与发电机轴连接。为保证整个升速过程力矩传递平稳,所有轮齿均为斜齿轮齿。

图1 风电机组齿轮箱内部结构图Fig.1 Wind turbine gearbox internal nomenclature
为保证监测数据的准确性,兼顾硬件设备存储能力,机组SCADA系统通常记录运行数据10 min的平均值。剔除状态类、开关量、标识类等参数后,SCADA系统监测的机组设备运行参数有47个(以桨叶角度、风速、温度、齿轮箱油温等数据为主)。参照能量在机组中的传递路径及表现形式,对机组运行参数进行分析,选择以下SCADA数据作为齿轮箱监测信息。
(1)风速v。风速指风来流方向的速度。当风速在机组切入风速至额定风速之间时,齿轮箱转轴转速与风速成正比。转速的上升会使齿轮摩擦加剧,振动增大,齿轮箱油温上升。
(2)齿轮箱油温T。风电机组通常采用浸油和飞溅的方式对齿轮箱中的部件进行润滑和降温,所以在确定的工况下,油温的变化反映了设备的运行情况。
(3)环境温度Te。环境温度在短时间尺度(一天)和长时间尺度(不同季度)中均有较大差异,温度变化会对齿轮箱油温和振动数据产生一定影响。
(4)风向角Ag。风向角指机舱与风来流方向形成的角度。风向角偏差过大会影响机组出力情况,同时,对风不准会使主轴承受更大的横向推力,加剧齿轮箱零件的磨损。
(5)有功功率P。负载增大时,输出功率增大,同工况下的齿轮箱振动和摩擦增大,油温升高。
通过现场调研发现,SCADA系统中的齿轮箱测点较少,而且缺少振动测点。为提高对齿轮故障诊断的准确性,需要在齿轮箱箱体特定部位增加振动测点,各测点信息如表1所示。

表1 测点位置及描述Tab.1 Acceleration sensor position and description
考虑到风速时变性对振动数据的影响,笔者采用阶比重采样的方法对齿轮箱振动数据进行预处理,将原本非平稳的振动信号进行平稳化处理,具体内容参考文献[12]。将处理后的齿轮箱角域信号进行峭度因子Kf和功率谱熵Hf的计算。
1.1 峭度因子Kf
设备运行正常时,Kf趋势无明显变化。一旦出现异常情况,Kf会有较为明显的趋势变化,并且有较为明显的单调性。Kf的表达式为
(1)
式中,xi为第i个监测数据;q为数据序列长度;σ为数据标准差。
当观测值的分散程度较小,冲击成分较多时,Kf增大;当观测值分散程度较大时,Kf减小[13]。
1.2 功率谱熵Hf
对齿轮箱角域信号进行阶比分析[4,12],得到阶比序列O,功率谱表达式为
(2)
式中,O(i)为序列O中第i个值;n为序列长度。
信号转换过程遵循能量守恒定律,因此阶比数据的功率谱熵表达为
(3)
与Kf类似,当设备运行状态发生变化时,Hf会出现较为明显的递增或递减趋势变化[14]。
因为振动数据与SCADA数据的采样频率不同,所以,对峭度因子Kf和功率谱熵Hf取10 min的平均值进行分析。
2 非线性状态估计的齿轮箱诊断模型
风电机组运行工况的时变性会导致其运行参数表现出较为明显的非线性,给数据特征分析带来影响,传统的分析方法通常不能明确机组运行数据的典型特征。本文采用非线性状态估计方法,并通过极限学习法对其进行合理改进,克服参数波动性对分析结果带来的影响,提升各参数间的相关性;应用因子分析方法,建立能够全面解释机组齿轮箱正常状态的样本数据,提高结果精度;通过滑动窗口与异常率方法对残差进行分析,保证最终结果的准确性。
2.1 非线性状态估计原理
针对风电机组齿轮箱运行特点,本文采用NSET[15-16]建立齿轮箱正常工况下的诊断模型。假设正常运行过程中,有n个相互关联的传感器对设备进行监测,在规定的时间内可得到一个矩阵,即过程记忆矩阵,其表达式为
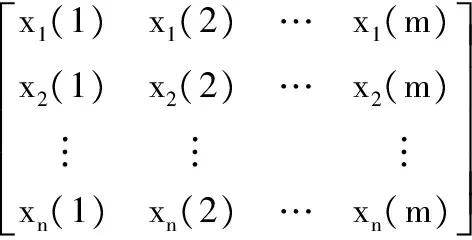
(4)
式中,X(i)为观测向量,表示设备在i时刻的运行状态。
将输入观测向量Xo放到过程记忆矩阵中,得到预测向量Xe:
(5)
其中,W为过程记忆矩阵的权值向量,可通过对Xo与Xe的残差ε=Xo-Xe进行极小化计算获得。
为保证残差值最小,进行如下计算:
(6)
对式(6)中的w求偏导,令S(w)为0,通过变换得
(7)
k=1,2,…,m
将式(7)转换成矩阵形式,并进行移项,得到W的表达式:
W=(DTD)-1(DTXo)
(8)
将式(8)代入式(5)得到预测向量的表达式:
Xe=DW=D(DT⊗D)-1(DT⊗Xo)
(9)
式中的⊗为非线性运算符。
当输入观测向量Xo为正常数据时,D中某些历史观测向量与之相近,NSET模型会获得预测精度较高的Xe,对应的残差绝对值|ε|较小;相反,当Xo为异常数据时,Xe的预测精度会降低,|ε|值较大。
2.2 基于极限学习机的NSET改进
由式(9)不难看出,权值向量W由过程记忆矩阵D和输入观测向量Xo计算得到。传统的NSET中,⊗通常表示两向量间的距离运算,如闵氏距离、马氏距离,但是这类运算均缺少对各参数间影响问题的分析。所以,本文采用极限学习机对NSET进行改进,分析观测向量中参数之间的影响,对参数赋予权重,建立参数之间的关联机制,提高NSET预测向量结果的准确性。
ELM是基于Moore-Penrose广义逆矩阵理论的单隐层前馈神经网络学习方法[17],通过随机输入权值和隐藏层阈值,可以确定一个可逆的隐层矩阵作为输出,将常规的数据训练转化成最小二乘问题,求取各输入参数的权值。
将过程记忆矩阵转置作为ELM的输入向量,目标函数t(i)=(t1(i),t2(i),…,tm(i))为期望输出向量,i=1,2,…,m,则ELM表达式如下:
(10)
j=1,2,…,m
式中,βi为第i个隐节点传递至输出层的权限,βi=[βi1βi2…βim]T;L为隐层节点数目,为保证权重数目与测点数一致,这里取L=n;ωi为输入层与隐层第i个神经元的权值向量;bi表示隐层第i个节点的偏置;g(x)为激活函数。
隐层输出矩阵H与目标输出矩阵T之间可用下式表示:
HB=T
(11)
H=
(12)
所以,输出权重为
Ba=H+T
(13)
式中,H+为矩阵H的Moore-Penrose广义逆矩阵;βai中的各值表示在i时刻各个参数的权重。
则过程记忆矩阵D为
D=[βa1X(1)βa2X(2)…βamX(m)]=
(14)
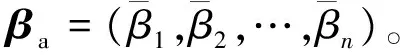
2.3 基于因子分析的过程构造记忆矩阵
文献[18]指出:从数据分析的角度看,设备的某种运行状态通常不是单一特征或几个孤立特征组合的集合,而是众多特征“稠密”排列的整体。结合本文研究内容,机组齿轮箱正常状态实际上也是多个连续动态过程的整体。所以,过程记忆矩阵D中的观测向量X(i)应尽可能覆盖齿轮箱正常状态下的动态过程。本文通过因子分析方法[19],寻找典型动态过程的数据特征,构建风电机组齿轮箱正常情况下的过程记忆矩阵。
因子分析是主成分分析的推广,它通过对各变量(参数)间复杂关系的解析,提取变量中联系紧密、特征表述明显的部分,用较少的变量综合反映变量整体的信息。对多个变量相关因素的优化不仅能够明确研究对象所处状态的典型特征,同时数据维数的降低也有助于提高状态分类的效率。过程记忆矩阵中观测向量的选取过程如下:
(1)对过程记忆矩阵进行标准化处理。
(2)对参数相关系数矩阵进行检验。各参数间存在较强相关性是因子分析的前提,通常对参数相关系数矩阵进行KMO(Kaiser-Meyer-Olkin)检测和巴特利特球度检验,验证所选数据是否适合因子分析。
(3)提取相关矩阵的主要成分。这里采用主成分分析法计算相关矩阵的特征值和特征向量,通过各参数累计方差贡献度λ确定主要成分个数。
(4)对已确定的主要成分进行旋转分析,调整参数在各主要成分中的载荷分布,以提高成分之间的差异性,明确各主要成分的实际意义。
(5)结合各观测向量,回归计算所有观测向量在各个主成分下的得分,并进行降序排列。其中,每个主要成分对应的是组成齿轮箱正常工况下的一个动态过程。主成分得分越高,对应观测向量的数据特征就越有代表性。所以,将各个主成分中得分较高的观测向量作为样本数据,增强样本数据对齿轮箱运行工况的解释能力,完成过程记忆矩阵的构造。
如图2所示,因子分析是对原本无序的各个观测向量进行基于状态的分类整理。通过寻找每个状态下的典型观测向量,完成过程记忆矩阵信息对设备工况特征的全面覆盖。
2.4 基于滑动窗口异常率的统计方法
由2.1节可知,NSET模型通过预测向量与观测向量间残差的大小来判断齿轮箱偏离正常状态的程度,判断齿轮箱异常与否通常由设定的残差阈值来实现。但是,数据受现场干扰和实际运行规程影响,简单通过设定残差阈值的方法很容易造成误报。例如,当齿轮箱油温高出阈值60 ℃时,油路中的散热系统启动,进行降温工作;受现场干扰,某些数据的突变也会使个别残差超出阈值。若单纯通过简单的阈值对机组设备运行状况进行评判,极易出现“误报”。所以,为保证模型诊断结果的准确性与可信性,采用滑动窗口[20]对残差值异常率进行统计分析。
设残差分析异常率滑动窗口区间[d,u],d为
窗口初始位置,u为窗口结束位置,长度为l。利用NSET模型经过一段时间预测,在滑动窗口中的预测残差序列为
εw=(εd,εd+1,…,εu)
(15)
结合实际经验,确定残差阈值Et。设在滑动窗口中各点的时刻标定序列为
Ts=(td,td+1,…,tu)
(16)
当某时刻的预测残差不在预先设定的阈值范围时,认为此时刻齿轮箱运行状态异常,对应时刻标定值置1。相反,则认为齿轮箱无异常情况,时刻标定值置0。滑动窗口中残差值异常率为
(17)
当实际的异常率ζ超过规定值时,认为齿轮箱出现异常情况。滑动窗口残差值异常率分析方法有以下优势:
(1)过程记忆矩阵的建立是一个数据统计过程,对于大多数正常情况的观测向量预测效果较好,但是当过程记忆矩阵的特征对输入向量表述不够充分时,NSET模型的预测效果会较差。通过滑动窗口中多个残差值异常率的计算,可有效减少由这些情况造成的分析结果不准确问题。
(2)机组在实际运行中,一些参数的异常变化并不意味着出现故障。通过滑动窗口异常率统计,可有效避免误报现象出现。同时,当齿轮箱出现故障时,随着滑动窗口的持续推移,最终的ζ会逼近1,这也保证了分析结果的可信性。
2.5 机组齿轮箱故障残差分析
为明确异常点的判定,需要通过确定阈值的方式对残差分析进行限定。将机组齿轮箱正常数据输入到建立好的NSET模型中,随着滑动窗口移动,会出现一系列的残差,计算每个窗口中残差序列的平均值,并取绝对值,找到其中的最大值,记为Ev,则机组齿轮箱正常情况阈值为
Et=kEv
(18)
其中,k可由统计分析或经验确定。
为消除观测向量存在的不确定性因素,认为残差均值服从正态分布[16],其置信度为1-α的置信区间为
(19)
式中,Ea为窗口中残差均值;S为窗口中残差值的标准差;N为残差计算时的窗口长度,N=100;tα/2为t分布的α/2分位点。
所以,窗口中的残差均值置信区间超过设定阈值Et表示当前时刻齿轮箱状态异常,标定值置1,异常率开始累加。当异常率大于规定阈值时,进行机组齿轮箱报警动作。
3 模型判定条件的确定
为实现NSET模型对齿轮箱运行状态的准确分析,选取国内某风场1.5MW双馈风电机组2012年3月份1 300组正常历史数据,随机选出500组作为训练数据,剩余的作为验证数据,对模型算法中涉及的判定条件进行确定。
3.1 观测向量参数权重的确定
通过极限学习机,对备选的500组训练数据进行各参数权重的分析。由2.2节可知,为保证权重与参数类型数量一致,隐层节点数L=7。输入层到隐层的连接权值ω和隐层所有节点的偏置b为(0,1)的随机数,激活函数选取Sigmoid函数。图3表示通过ELM分析得到的前50组观测向量中各参数权重,其中,观测向量数记为M。
输入观测向量Xo中各参数的权重如表2所示。

(a)参数权重1
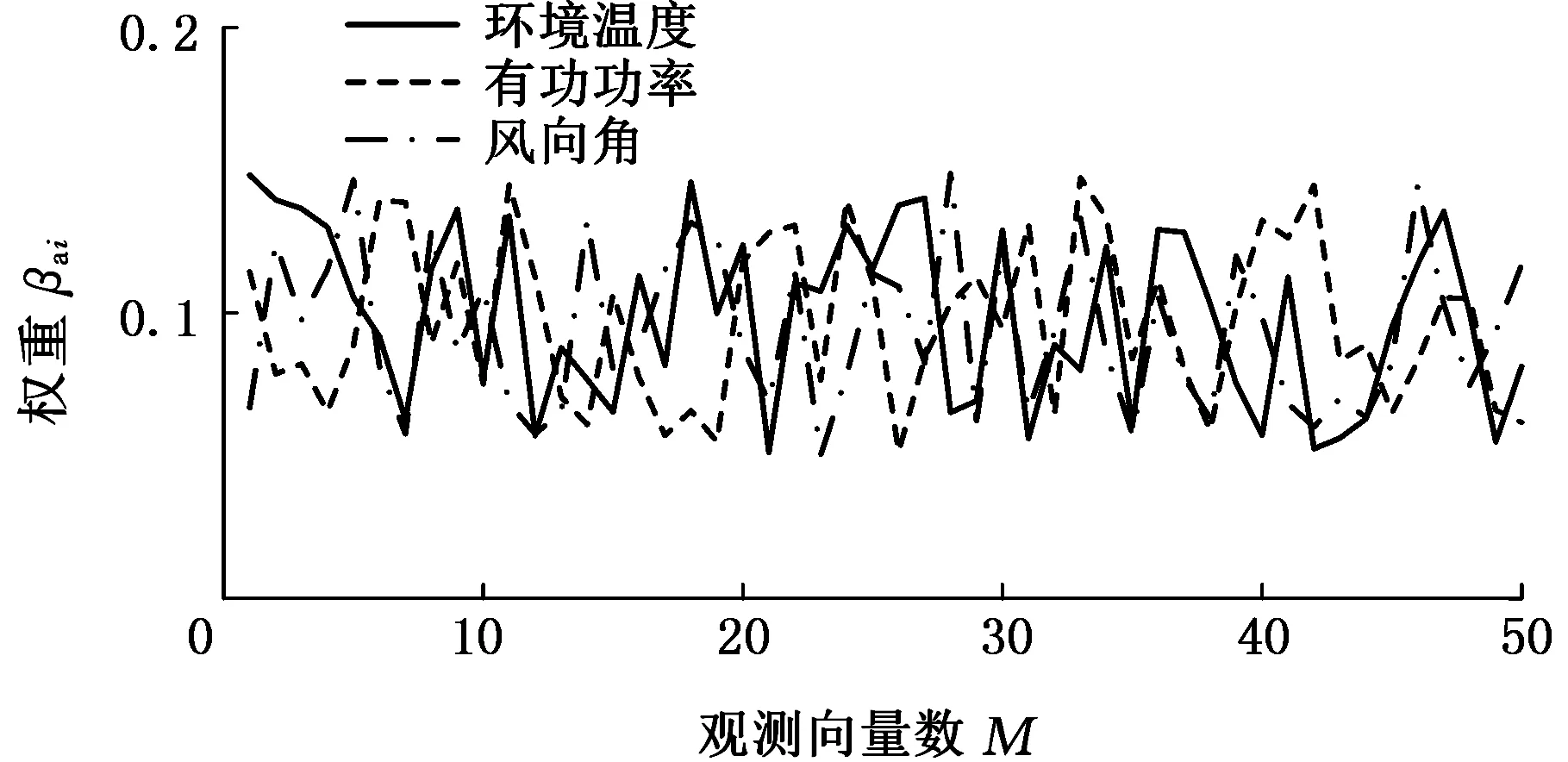
(b)参数权重2图3 观测向量参数权重分布Fig.3 Observation vector parameter weight distribution

表2 观测向量各参数权重Tab.2 Observation vector parameter weight
3.2 过程记忆矩阵的确定
将赋予参数权重的500组训练数据形成原始过程记忆矩阵,建立各参数间的相关系数矩阵,并进行相关性分析。其中,各参数KMO测度为0.675,大于0.6,说明各参数间关联性较强。巴特利特球度检验的观测值为201.011,相应的显著性水平为0,表明样本充足,适合进行因子分析。计算相关系数矩阵的特征根和贡献度,结果如表3所示。
根据方差累计贡献度超过85%的要求可知,经过旋转分析,表3中前4个成分的累计贡献度已达到94.09%,故确定主要成分个数为4,即齿轮箱正常情况下主要由4个动态过程组成。为明确各个主要成分(动态过程)对参数的解释,需要再次进行成分旋转。本文采用Kaiser方差最大旋转,计算主要成分与原有参数的载荷值,如表4所示。
每个成分中参数的载荷越大,该成分包含对应参数信息的内容就越多。其中,成分1(振动成分)中支配的是与振动相关测参数;成分2(温度成分)中支配的参数为齿轮箱油温和环境温度;成分3(功率成分)主要支配风速和有功功率参数,与机组的功率相关;成分4(角度成分)主要与风向角度有关。应用回归计算得出各成分在每个观测向量下的得分,结果如表5所示。
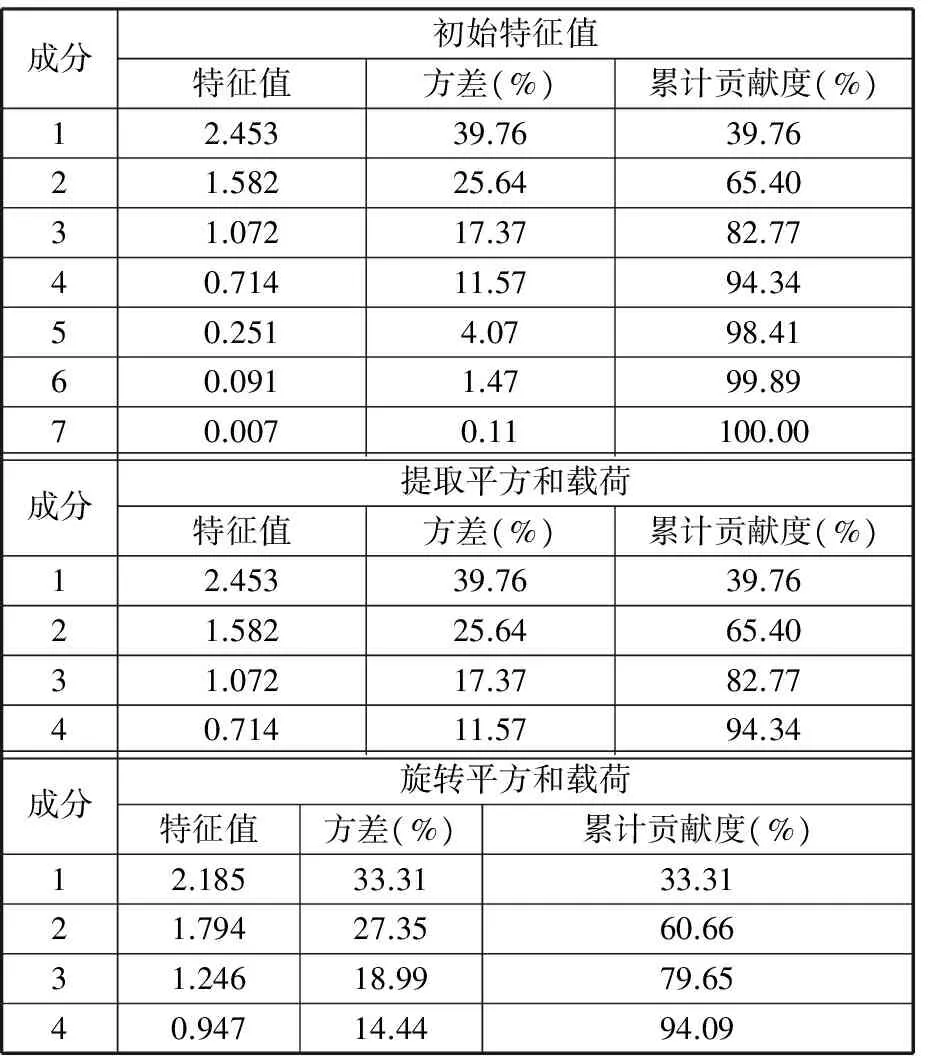
表3 成分解释原参数方差的情况Tab.3 Ingredients explain the variance of the original parameters
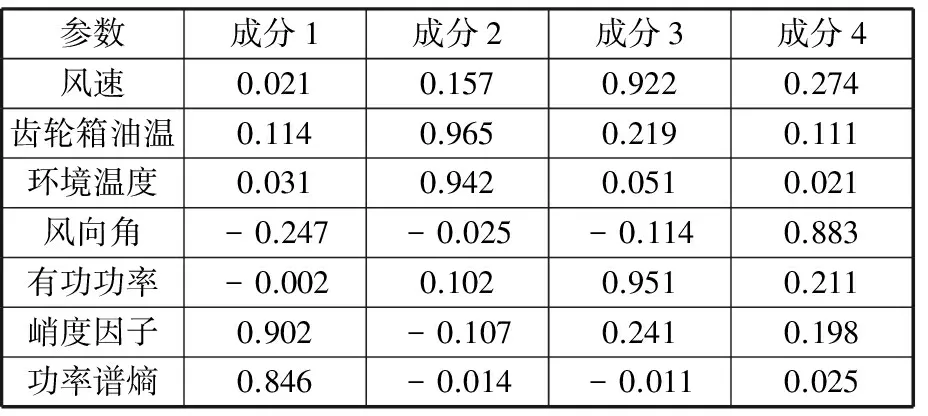
表4 旋转成分矩阵Tab.4 Rotated component matrix
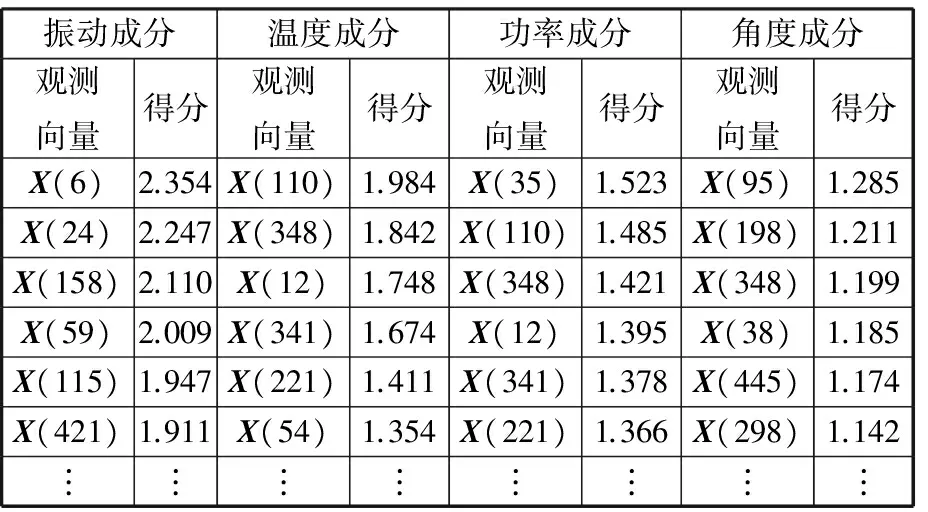
表5 成分得分Tab.5 Ingredient score
各成分中的向量得分已经过降序排列,在某一成分下,观测向量得分越高,其对该成分的解释能力越强,在该成分对应的动态过程中越具有代表性。所以,根据各主要成分得分的排序结果,按照各个主成分方差累计贡献度的比例进行选取,组成风电机组齿轮箱正常情况下的记忆过程矩阵。本文选取振动成分前20%、温度成分前15%、效率成分前10%、角度成分前7%的观测向量组成过程记忆矩阵。
3.3 滑动窗口和异常率参数的确定
将建立好的过程记忆矩阵对剩余800组数据进行预测,得到正常情况下滑动窗口残差均值分布,如图4所示。由图4可知,Ev=0.053。本文取k=1.1,将Ev和k代入式(18),计算得到齿轮箱的故障阈值Et=0.058。

图4 正常情况残差分布图Fig.4 Normal condition residual distribution
已知同一机组于2010年4月18日至23日齿轮箱出现故障,此时段共有750组数据,将其作为NSET模型的输入,得到残差图(图5)。
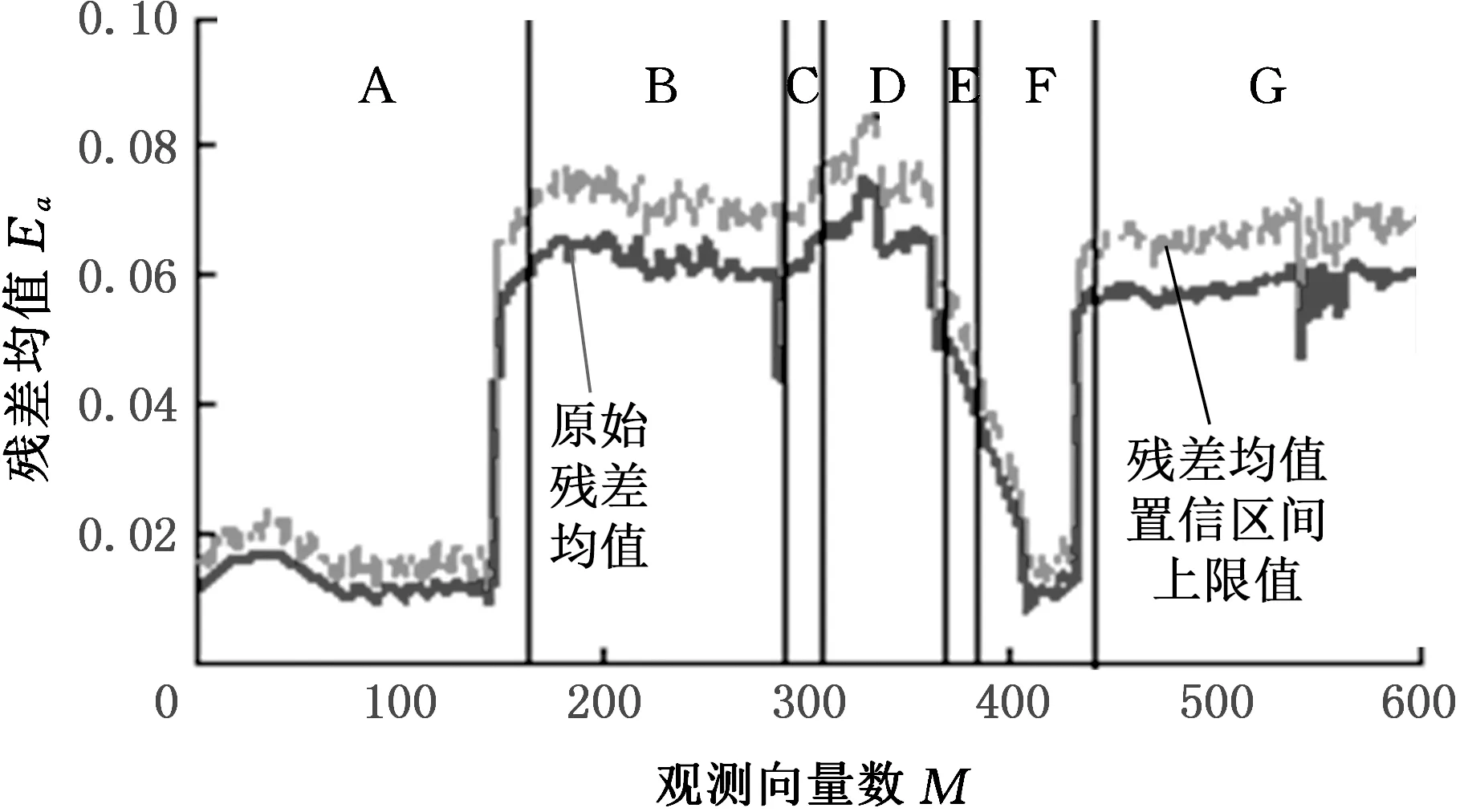
图5 齿轮箱故障残差分布图Fig.5 Gearbox fault residual distribution
根据图5中残差曲线在不同时段的特征,将其按时间分成A~G七个区域,各区域的具体描述如表6所示。
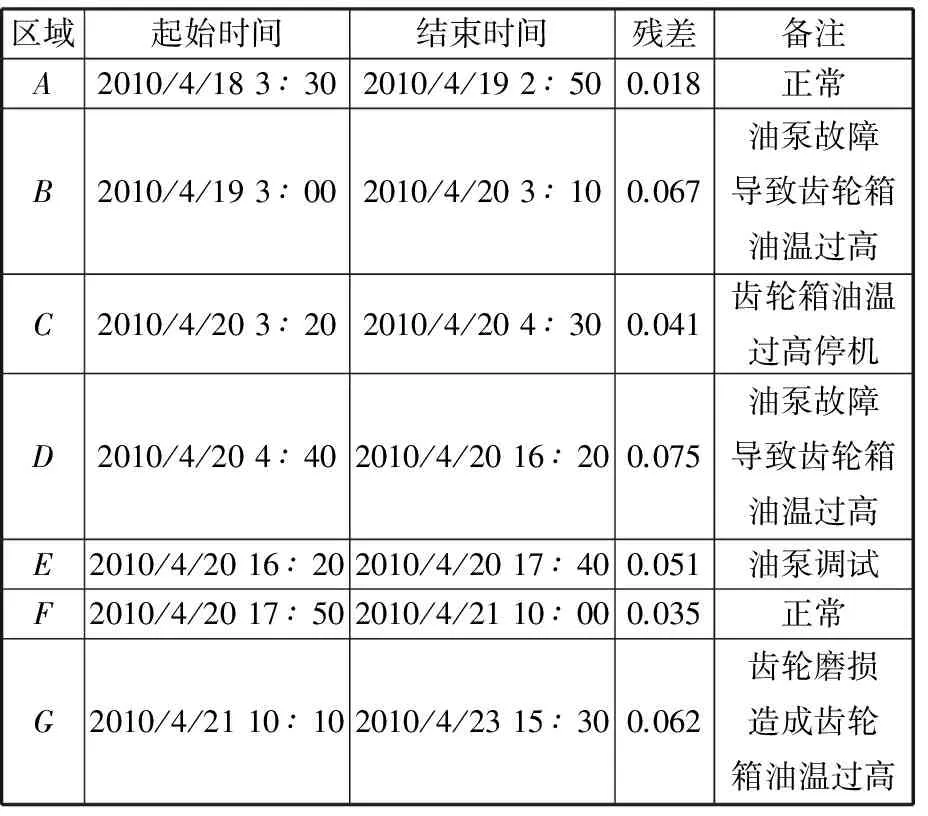
表6 各区域齿轮箱状态描述Tab.6 Status description of gearbox in each area
机组于B区出现齿轮箱油温过高情况,残差值超出阈值,此时油路中的冷却系统启动,防止油温继续上升,所以整个B区残差随时间没有明显变化;C区因油温持续过高,机组进行保护性停机动作;D区为机组重新启动后,齿轮箱油温过高情况未得到有效缓解,残差依旧较大;E区表示人为停机动作,进行齿轮箱油泵修理工作;F区表示油路循环功能恢复,此时段机组工作正常,残差出现较为明显的下降趋势;G区因齿轮箱存在齿轮磨损故障,造成油温升高,使残差大于阈值。
观察整个残差曲线分布:在曲线B区和D区,齿轮箱出现了油泵故障和齿轮磨损故障,而且,D区的磨损故障要严重于B区,所以残差较大;油泵修复后,齿轮磨损故障导致G区的残差超过阈值,但此时间段只受单一故障影响,故G区的残差低于B区和D区。
F区表示通过现场检修出现一段“正常”时期,异常率窗口滑动到此区间时,异常率不应受到G区故障影响。所以窗口长度应当不超过F区长度;机组在整个运行过程中出现过短暂的“调整”(C和E区),要确定的异常率阈值应能区分出这两个区域,而不被周围的故障数据干扰。
所以,考虑到以上这些情况,确定异常率滑动窗口长度l=40。通过改变异常率阈值,对机组齿轮箱进行诊断,结果如表7所示。表7中A~G代表图5中对应的时间区域,“√”表示在既定异常率阈值下,滑动窗口可察觉出对应时间区域的机组状态,“×”则反之。
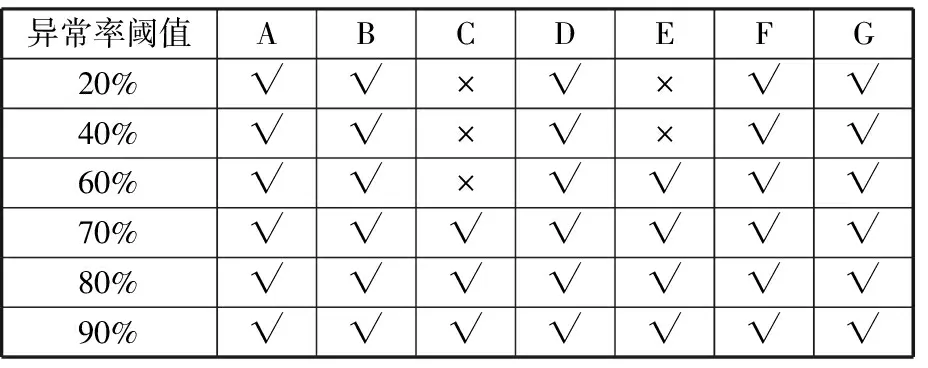
表7 诊断结果表Tab.7 Diagnostic results
当异常率大于70%时,机组各个阶段运行状态均可准确察觉。所以,对于机组齿轮箱故障诊断,窗口长度l=40,异常率阈值ζt=70%。
4 实例验证
为验证文章提出方法的准确性与可行性,以河北省沧州市某风场1.5MW双馈风电机组为例。已知该机组于2014年3月13—17日出现行星轮系太阳轮轮齿磨损情况。采用文中提出的模型进行分析,残差均值和滑动窗口异常率结果如图6所示。其中,残差滑动窗口数记为Rw,异常率滑动窗口数记为Aw。
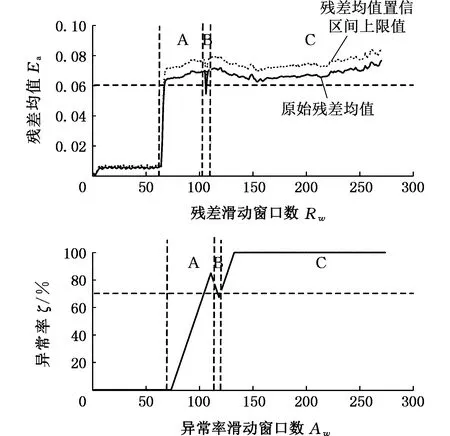
图6 齿轮箱故障偏差与异常率统计Fig.6 Gearbox failure deviation and anomaly statistics
从图6中可以看出:残差均值95%置信区间的上限在第68个窗口开始超过残差阈值,即残差曲线图中的A区域,此时异常率开始上升,一直到第97个窗口时,异常率超过阈值;B区为机组因运行参数异常进行的短时间保护性降负载过程,此时残差和异常率均回落到阈值以下;C区中,在第110个残差窗口时,机组恢复原始工作状态,残差因机组异常状态影响继续上升,并超过残差阈值。在第116个异常率滑动窗,异常率超过阈值,并继续上升至1,说明机组齿轮箱此时已经出现了异常情况。虽然在异常率第一次超出阈值后出现了回落,但观察整个异常率曲线发现,异常率最终上升至1,说明第一次阈值超限对齿轮箱异常情况判断的结果也是准确的。
采用传统的NSET方法对同一组数据进行分析。其中,齿轮箱故障征兆阈值Et=0.031,残差和异常率如图7所示。
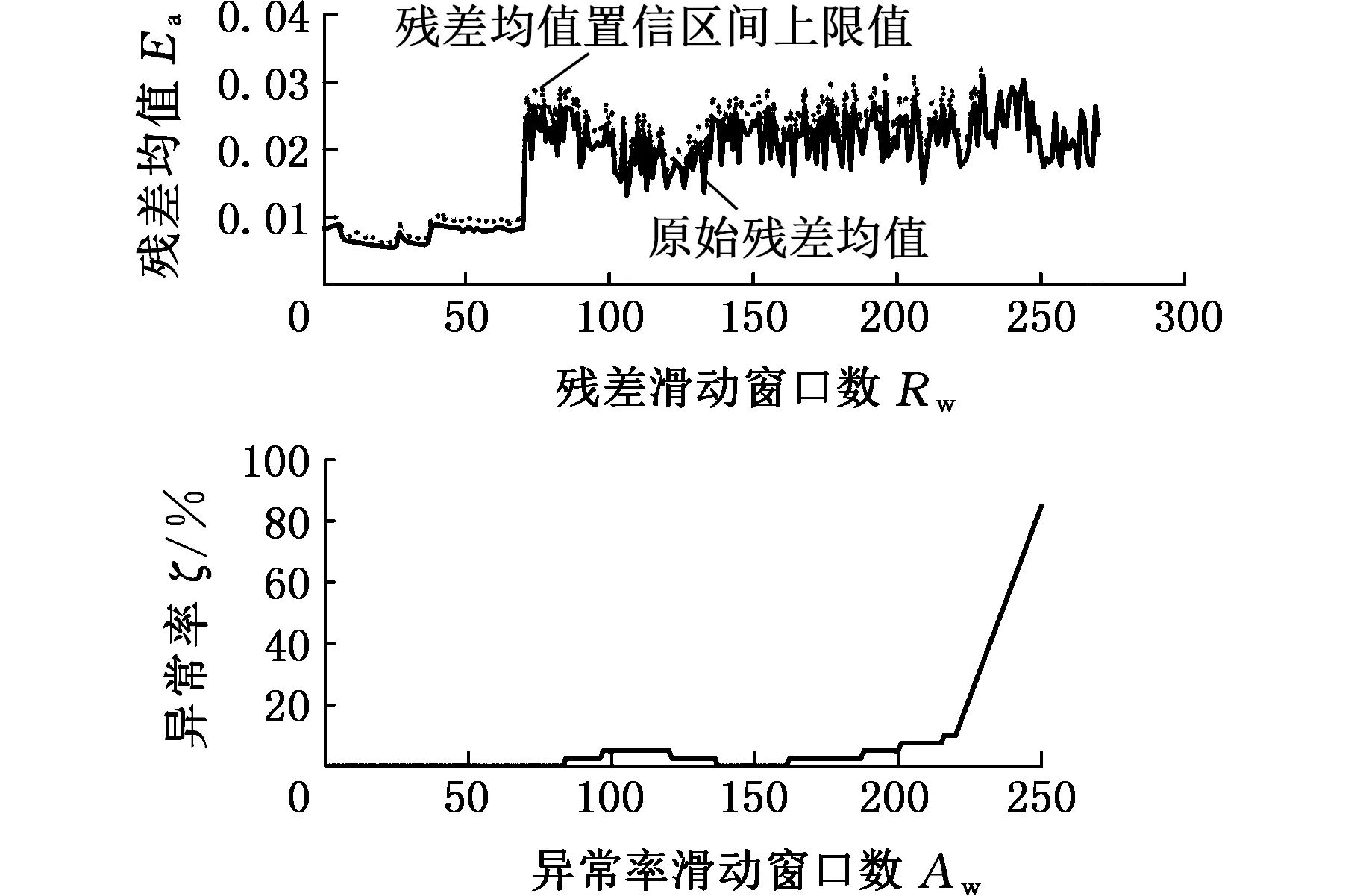
图7 传统方法的齿轮箱故障偏差与异常率统计Fig.7 Gearbox failure deviation and anomaly statistics by conventional method
通过结果对比不难看出,传统方法计算的残差整体变化幅度不明显,且数据波动较大。同时,异常率达到阈值上限的窗口位置为第239个,明显晚于改进算法,说明本文提出的模型能够更准确、更及时地察觉机组齿轮箱异常情况。
5 结论
(1)通过ELM对NSET方法进行合理改进,对机组齿轮箱各运行参数的权重进行赋值,明确了各运行参数间的相关性,确保预测向量的精度。
(2)运用因子分析方法对机组齿轮箱正常情况下动态过程进行解析,建立了各动态过程与运行参数之间的关联机制,通过合理选取具有代表性的观测向量,提升记忆过程向量数据信息对工况特征的覆盖能力。同时,缩小样本数据空间,减轻运算压力。
(3)将滑动窗口与异常率方法结合,有效避免数据波动和随机性对最终分析结果的影响。同时,该方法充分考虑了风电机组实际运行情况,对模型参数进行合理配置,可提升最终分析结果的可信性。
参考文献:
[1]TONY B.Wind Energy Handbook[M].Beijing: Science Press,2009.
[2]杨锡运,郭鹏,岳俊红.风力发电机组故障诊断技术[M].北京:中国水利水电出版社,2015.
YANG Yunxi,GUO Peng,YUE Junhong.Wind Turbine Fault Diagnosis Technology[M]. Beijing:China Water & Power Press,2015.
[3]李辉,胡姚刚,李洋,等.大功率并网风电机组状态监测与故障诊断研究综述[J].电力自动化设备,2016,36(1):6-16.
LI Hui,HU Yaogang,LI Yang,et al.Overview of Condition Monitoring and Fault Diagnosis for Grid-connected High-power Wind Turbine Unit[J]. Electric Power Automation Equipment,2016,36(1):6-16.
[4]LINDEN D V D,SITTER G D,VERBELEN T,et al. Towards an Evolvable Data Management System for Wind Turbines[J].Computer Standards & Interfaces,2017,51:87-94.
[5]赵洪山,张路朋.基于可靠度的风电机组预防性机会维修策略[J].中国电机工程学报,2014,34(22):3777-3783.
ZHAO Hongshan,ZHANG Lupeng. Preventive Opportunistic Maintenance Strategy for Wind Turbines Based on Reliability[J].Proceedings of the CSEE,2014,34(22):3777-3783.
[6]WYMORE M L,DAM J E V,CEYLAN H,et al.A Survey of Health Monitoring Systems for Wind Turbines[J]. Renewable & Sustainable Energy Reviews,2015,52:976-990.
[7]SCHLECHTINGEN M,SANTOS I F,ACHICHE S. Wind Turbine Condition Monitoring Based on SCADA Data Using Normal Behavior Models.Part 1:System Description[J]. Applied Soft Computing,2013,13(1):259-270.
[8]SCHLECHTINGEN M,SANTOS I . Wind Turbine Condition Monitoring Based on SCADA Data Using Normal Behavior Models. Part 2:Application Examples[J]. Applied Soft Computing,2014,14(1):447-460.
[9]李状,柳亦兵,马志勇,等.结合C-均值聚类的自适应共振神经网络在风电机组齿轮箱故障诊断中的应用[J].动力工程学报,2015,35(8):646-651.
LI Zhuang,LIU Yibing,MA Zhiyong,et al.Application of ART2 Neural Network Combined with C-means Clustering in Fault Diagnosis of Wind Turbine Gearbox[J]. Journal of Chinese Society of Power Engineering,2015,35(8):646-651.
[10]向玲,鄢小安.基于小波包的EITD风力发电机组齿轮箱故障诊断[J].动力工程学报,2015,35(3):205-212.
XIANG Ling,YAN Xiaoan.Fault Diagnosis of Wind Turbine Gearbox Based on EITD-WPT Method[J]. Journal of Chinese Society of Power Engineering,2015,35(3):205-212.
[11]黎涛,唐明珠,谭欣星.基于CLSSVM的风电机组齿轮箱故障诊断[J].可再生能源,2015,33(2):232-237.
LI Tao,TANG Mingzhu,TAN Xinxing.Fault Diagnosis of Wind Turbine Gearbox Based on Cost-sensitive Least Squares Support Vector Machine[J].Renewable Energy Resources,2015,33(2):232-237.
[12]顾煜炯,贾子文,王瑞,等.基于改进的多元离群检测方法的风机齿轮箱早期故障诊断[J].中国机械工程,2016,27(14):1905-1910.
GU Yujiong,JIA Ziwen,WANG Rui,et al.Early Fault Diagnosis for Wind Turbine Gearbox Based on Improved Multivariate Outlier Detection[J].China Mechanical Engineering,2016,27(14):1905-1910.
[13]孟宗,李晶,龙海峰,等.基于压缩信息特征提取的滚动轴承故障诊断方法[J].中国机械工程,2017,28(7):806-812.
MENG Zong,LI Jing,LONG Haifeng,et al.Fault Diagnosis Method for Rolling Bearings Based on Compression Information Feature Extractions[J].China Mechanical Engineering,2017,28(7):806-812.
[14]郭厚明,行志刚,荆双喜.无量纲参数在矿用低速重载齿轮故障诊断中的应用[J].煤炭科学技术,2006,34(8):28-31.
GUO Houming,XING Zhigang,JIN Shuangxi. Dimensionless Parameters Applied to Fault Diagnosis of Mine Low Speed Heavy Loaded Gear[J].Coal Science and Technology,2006,34(8):28-31.
[15]尹诗,余忠源,孟凯峰,等.基于非线性状态估计的风电机组变桨控制系统故障识别[J].中国电机工程学报,2014,34(S1):160-165.
YIN Shi,YU Zhongyuan,MENG Kaifeng,et al.Fault Identification of Pitch Control System of Wind Turbine Based on Nonlinear State Estimation [J]. Proceedings of the CSEE,2014,34(S1):160-165.
[16]郭鹏, INFIELD D, 杨锡运.风电机组齿轮箱温度趋势状态监测及分析方法[J].中国电机工程学报, 2011, 31(32):129-136.
GUO Peng, INFIELD D, YANG Xiyun.Wind Turbine Gearbox Condition Monitoring Using Temperature Trend Analysis[J].Proceedings of the CSEE,2011,31(32):129-136.
[17]何群,李磊,江国乾,等.基于PCA和多变量极限学习机的轴承剩余寿命预测[J].中国机械工程,2014,25(7):984-989.
HE Qun, LI Lei,JIANG Guoqian, et al.Residual Life Predictions for Bearings Based on PCA and MELM[J]. China Mechanical Engineering,2014,25(7):984-989.
[18]CHANDOLA V,BANERJEE A,KUMAR V. Anomaly Detection:a Survey[J]. ACM Computing Surveys,2009,41(3):1-58.
[19]王淑芬.应用统计学[M].北京:北京大学出版社,2011.
WANG Shufen.Applied Statistics[M].Beijing:Peking University Press,2011.
[20]刘涛,刘吉臻,吕游,等.基于多元状态估计和偏离度的电厂风机故障预警[J].动力工程学报,2016,36(6):454-460.
LIU Tao,LIU Jizhen,LYU You,et al.Early Fault Warning of Power Plant Fans Based on MSET and the Deviation Degree[J].Journal of Chinese Society of Power Engineering,2016,36(6):454-460.
(编辑张洋)

