第一性原理研究Zr的掺杂对Xe在UO2中溶解能力的影响∗

张仲 王欢 王开元 安欢 刘彪 伍建春 邹宇

(四川大学原子核科学技术研究所,辐射物理及技术教育部重点实验室,成都 610064)

1 引 言

作为人类最具希望的未来能源之一,核能的发展备受关注[1,2].人们开发核能有两种途径:重元素的裂变和轻元素的聚变.裂变主要利用的是U元素吸收热中子后释放的裂变产物所携带的能量.目前世界上运行中的核反应堆大多数都是轻水堆,UO2是堆中主要的燃料,它具有高熔点、抗辐照、抗腐蚀,与包壳材料的相容性好以及强的包容裂变气体能力等优良性能[3].

核反应堆在运行时,堆芯中的燃料芯块UO2在裂变过程中会不可避免地产生大量裂变产物,其中Xe等气体裂变产物引起的肿胀是核反应堆燃料元件中最重要的问题之一,它们会对核燃料UO2内部的温度场和结构力学场的演化产生直接的影响,从而难以预测燃料内部的行为,增加了核反应堆工作过程中的安全隐患.另外Xe也可能是引起UO2晶粒亚晶化的诱因之一.在此过程中,最初的一个粒径为10µm的UO2晶粒变成了104—105个0.2µm的亚晶粒[4].

反应堆中每次U裂变都会在UO2晶格中释放约200 MeV的能量.分子动力学研究表明,高能裂变产物轰击UO2后,在UO2中会形成U和O的Frenkel缺陷,然后这些Frenkel缺陷会通过扩散等方式在UO2晶格中形成Schottky缺陷[5,6].而裂变Xe原子在燃料相晶粒内产生后,会被燃料相中的点缺陷、位错和空洞等缺陷俘获[7].Yun等[8]对UO2中VO,VU,VUO,VUO2,VU2O2等空位缺陷辅助Xe扩散机理进行了研究;Andersson等[9]在研究UO2中Xe迁移机理的过程中发现Xe还会通过VU2,VU2O缺陷进行迁移,进而又发现掺杂到UO2中的Xe原子会与空位团簇VU3O结合[10].

水冷堆中核燃料组件主要选用Zr合金作为其包壳材料,高温下Zr与UO2中的原子会发生相互扩散;同时Zr也是一种裂变产物,因此不可避免地会有部分Zr掺入核燃料UO2中.在一些特殊反应堆中,为了提高UO2的燃耗,增强辐照的稳定性,也考虑添加Zr元素取代U原子形成ZrUO2固溶体燃料[11−13].Zr的引入会影响到裂变产物Xe在UO2中的溶解行为.因此,本文基于密度泛函第一性原理和缀加平面波赝势方法(PAW),通过计算UO2中Zr掺杂前后空位缺陷的形成能和Xe吸附的结合能的变化情况,研究了Zr的掺杂对裂变产物Xe在UO2中的溶解能力的影响,为实际应用提供了理论参考.

2 建立模型及计算方法

UO2的晶体结构为FCC结构,空间群为225/Fm¯3m,实验测得其晶格常数a=5.468 Å[14].O和U原子的晶格位置分别为(0.25,0.25,0.25)、(0,0,0),由此建立UO2的单胞结构模型如图1(a)所示,其中O原子位于U原子构成的面心立方点阵的四面体间隙处.缺陷形成能的计算采用超元胞结构,综合考虑了计算机的计算能力和结果的准确性,本文中选取3个基矢方向均扩展为2个单位的2×2×2的UO2超元胞结构,其中含有32个U原子和64个O原子.由于Zr原子掺杂进入UO2中,受到原子间相互作用及电负性、半径等因素的限制,主要取代U形成ZrUO2固溶体,并且保持原晶体对称结构不变[13,15].因此,我们在建立的UO2超元胞的基础上将一个U原子替换为Zr原子,得到Zr掺杂的UO2超元胞(文中用Zr-UO2表示)结构模型,如图1(b)所示.

本文所有计算工作均利用基于密度泛函理论的VASP(Viennaab-initiosimulation package)软件包进行[16,17],体系的价电子与离子实之间的相互作用采用PAW[16]进行处理,电子之间的交换关联势采用Perdew-Burke-Ernxerhof形式的广义梯度近似[18]的泛函进行描述.考虑到UO2是强关联电子体系,于是加入了HubbardU[19]修正,U和J的值分别取4.50 eV和0.51 eV[20,21](Ueff=U−J).经过截断能收敛性测试,设置计算中的平面波截断能为400 eV,又设置自洽收敛精度为1×10−4eV,布里渊区采用Monkhorst-Pack方法自动生成的5×5×5网格描述,倒空间中积分的分布函数采用高斯分布函数,展宽设置为0.05 eV.实验结果表明UO2为3 K反铁磁体系,但有计算结果表明采用1 K反铁磁体系不仅可以简化计算,且计算结果与3 K反铁磁体系很接近[22],因此所有结构的全弛豫计算均采用1 K反铁磁进行考虑.

对于UO2与Zr-UO2中空位缺陷的形成能,计算公式为:

其中Ef(VX)是一个X空位缺陷的形成能,Etot(VX)是晶胞中含有一个X空位缺陷时的总能量;nU和nO分别为含缺陷的晶胞相对无缺陷的原始晶胞缺少的U和O原子的数目;µU和µO分别为U原子和O原子的化学势;Eperf为原始晶胞的能量.

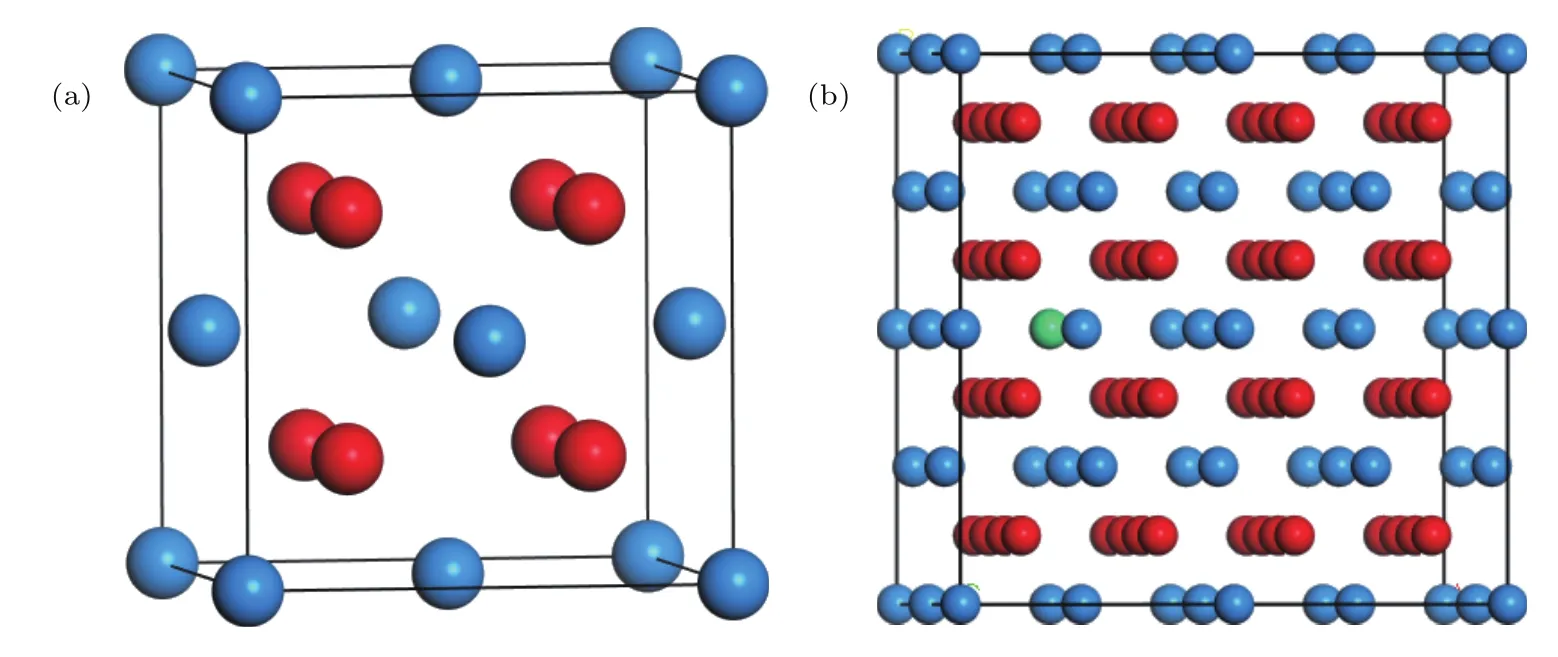
图1 计算体系的结构模型 (a)UO2单胞;(b)Zr-UO2超胞(2×2×2);其中蓝色表示U原子,红色表示O原子,绿色表示Zr原子Fig.1.Structure models of calculation systems:(a)UO2sigle-cell;(b)Zr-UO2supercell(2×2×2).The blue,red and green balls denote U,O and doping atom Zr.

由于U原子和O原子的化学势是未知的,于是分别取α-U和O2分子作参考态,并结合公式:

在计算UO2中空位缺陷形成能时,由于µU,µO可在一个范围内变化,于是对U富集和O富集两种情况[23,24]进行了考虑,分别对应µU取上限值和µO取上限值.其中,µUO2为计算得到的单个UO2分子的能量,其值为−29.15 eV.在U富集条件下,取α-U的能量为µU,由(2)式即可得到µO;在O富集条件下类似,取O2分子能量的一半为µO,再由(2)式得到µU.计算得到O2分子和α-U的能量分别为−9.86 eV和−8.22 eV,与文献[25]值报道的−9.78 eV,−8.08 eV基本一致.于是得到µU,µO的取值范围:

则:U富集时取µU=−8.22 eV,µO=−10.46 eV;O富集时取µO=−4.93 eV,µU=−19.26 eV.

而晶胞中Xe吸附的结合能则采用计算公式:

其中,Eb(XeX)是在Xe吸附到X缺陷的结合能;Etot(XeX)是Xe吸附到X缺陷后体系的总能量;EXe是Xe原子的参考能量,经计算得到其值为−0.012 eV.

晶胞中Xe的溶解能即为空位缺陷的形成能与其对应的Xe吸附的结合能之和,因此计算公式为:

其中,Es(XeX)是Xe溶解到X缺陷中所需的溶解能.

3 结果与讨论

考虑到以往文献中基本没有系统地研究Ueff=3.99 eV时U,O富集情况下各缺陷的形成能,为了验证计算方法的可行性,选择取Ueff=3.0 eV,计算出UO2中各点缺陷的形成能并与文献值[14]进行比较,如表1所列.计算结果与文献值很接近,说明计算方法可行.

计算得到Ueff=3.99 eV时Zr掺杂前后UO2中空位缺陷的形成能如表2所列.对比U富集和O富集时空位形成能容易发现,除VUO2外,缺陷在两种情况下形成能差异较大.这表明同种缺陷在不同化学配比的UO2中的形成难易程度有较大差别.而在实际反应堆中UO2的化学配比会随着反应的进行发生变化,因此缺陷的形成难易程度也会随之发生变化,进而改变体系中缺陷的相对数目.

表1 Ueff=3.0 eV时UO2中点缺陷的形成能(eV)Table 1.Formation energies of point defects in UO2 while Ueff=3.0 eV(eV).

表2 UO2和Zr-UO2中空位缺陷的形成能,ΔEf表示Zr掺杂后缺陷形成能的变化量(eV)Table 2. Formation energies of vacancy defects in UO2and Zr-UO2,ΔEfrepresents the formation energy variation after the Zr doping(eV).

Van Brutzel等[5]通过分子动力学方法模拟了离位原子在UO2中引入的缺陷,发现UO2中辐照产生的O的Frenkel缺陷的数量远多于U的Frenkel缺陷.如表2所列,通过计算可以看到,UO2中U富集时O空位的形成能比U空位低很多,说明O空位相比U空位更容易形成,因此UO2中离开晶格点阵位置形成离位原子的绝大部分是O原子,这就解释了他们的研究结果.而且,对比VU,VUO,VUO2和VU2,VU2O,VU2O2缺陷的形成能大小关系可知,随着组成缺陷的O空位数目逐渐增加,其形成能逐渐减小,说明UO2中U空位有与O空位结合的趋势,且在一定范围内,结合的O空位越多越稳定.这与他们对Frenkel缺陷扩散后形成Schottky缺陷研究结果基本一致.同时,他们还发现UO2中的O,U空位可以形成最多由18个点缺陷组成的团簇,但其数量非常少,主要含有2—3个点缺陷组成的团簇,而从表2中的研究结果可以看到U富集时VUO,VUO2是形成能最低的团簇,说明它们很容易形成,两者结论十分符合.并且在所有空位缺陷中,O空位的形成能最低,而形成能最低的团簇是VUO2,可见缺陷的形成能并不会单纯随缺失原子数目的增加而增加,原子间的相互作用也是重要的影响因素.

而在O富集时,大部分空位缺陷的形成能为负值,说明此时空位缺陷大多都已比较容易形成,结合之前的分析可知,此时O含量较多,而O比较容易成为离位原子,形成的O空位与U空位结合会降低缺陷的形成难度,因此缺陷的形成能普遍降低.但同时会使得单独存在的VO缺陷很难存在,因此VO的形成能却增加很多.

Zr掺杂后,各空位缺陷的形成能都有不同程度的增加,但不同缺陷之间的形成能大小关系却没有发生变化.究其原因,虽然Zr原子的电负性略弱于U原子,其吸引电子的能力更弱,但由于它们的电负性都比较小,且立方相ZrO2与UO2具有相同的晶体结构,经计算可知其中Zr4+和U4+的离子半径仅相差约0.1 Å,因此Zr掺杂到UO2中取代一个U原子的影响较小,会改变形成能的大小,但不会从根本上改变各缺陷形成能的大小关系.同时,对于由3个及3个以上点缺陷组成的团簇,Zr的掺杂对其形成能的影响基本就比较小了.缺陷形成能的增加说明Zr掺杂可以起到阻碍UO2中空位缺陷的形成的作用,对于体系中含量较多的团簇缺陷,VUO,VUO2的形成能变化量相差最大,因此可以预期,当Zr-UO2受辐照时,晶体内VUO,VUO2团簇的相对数量相比UO2中可能会发生较大的变化.

为了考察体系中Zr的存在对Xe掺杂的影响,我们对Xe吸附到空位缺陷所需的结合能进行了计算,结果如表3所列.UO2中,Xe吸附到VU3O缺陷的结合能仅有0.53 eV,在所有吸附体系中最低,说明Xe更多的是吸附到VU3O缺陷中.随着Zr掺杂形成Zr-UO2固溶体,Xe吸附的结合能有增有减,且随着缺陷复杂程度的增加先减小后增大,说明Zr的掺杂会降低Xe原子在简单缺陷中的吸附难度,而增加在复杂缺陷中的吸附难度,因此会使得材料复杂缺陷中的部分Xe原子有转移到更简单的缺陷中的趋势.

表3 Xe吸附的结合能,ΔEb表示Zr掺杂后结合能的变化量(eV)Table 3. Binding energies of Xe adsorption,ΔEb represents the binding energy variation after Zr doping(eV).

考虑到Xe是惰性气体,和缺陷所带的电荷不会发生作用,Xe吸附的结合能可能只和空位缺陷的孔隙尺寸有关.我们取缺陷体系所形成孔隙中所能放入最大球体的半径为缺陷的孔隙半径,对各空位缺陷在Xe掺杂前后的孔隙半径差ΔR与Xe吸附所需结合能Eb的相互关系进行了研究,所得结果如图2所示.容易发现,Xe吸附的结合能与其吸附前后孔隙半径差的变化趋势一致,均随着缺陷复杂程度的增加而减小,说明缺陷的尺寸对结合能的大小起主要作用.图中Eb/ΔV与缺陷的变化关系曲线则表示Xe吸附后改变单位体积的孔隙尺寸所需要的能量,可见在UO2中其会随着缺陷复杂程度的增加而减小,但对于Zr-UO2中的空位团簇则变化不大,说明Zr的存在对Xe吸附引起的孔隙尺寸变化单位体积所需能量也有一定影响.结合孔隙尺寸的影响,分析可知这主要是由于惰性元素不会与周围原子成键,因此其所吸附的空位尺寸越大,所需的结合能也就越小.Zr则主要通过影响周围原子排布,进而改变孔隙尺寸来影响Xe的吸附.

为了获得UO2中Zr的掺杂对Xe的溶解能力的影响,我们对空位缺陷的形成能和Xe吸附的结合能进行了加和,得到了Xe的溶解能结果,如表4所列.可见U富集和O富集两种情况下Xe的溶解能存在较大差异,因此在实际反应堆中,Xe在UO2空位缺陷中的溶解能力也会随着反应的进行而发生变化.同时,Zr掺杂后,除了Xe在VU和VUO2中的溶解能有极小的减小之外,在其他缺陷中都有一定程度的增加.比较空位缺陷和Xe吸附的结合能变化量可知,空位缺陷的形成能变化量普遍更大,而VU2O2和VU3O缺陷本身的形成能变化量虽然较小,但所对应的Xe吸附的结合能是增加的,使得Xe的溶解能增加.这说明Zr的掺杂主要通过增大空位缺陷的形成难度而从总体上减小了Xe在UO2中的溶解能力.

图2 Xe吸附的结合能与空位缺陷孔隙半径变化的关系(ΔR表示Xe吸附前后各空位缺陷的孔隙半径差) (a)UO2;(b)Zr-UO2Fig.2.Relationship between binding energies of Xe adsorption and pore radius of vacancy defects,ΔR represents the void radius variation of each vacancy defect after Xe adsorption:(a)UO2;(b)Zr-UO2.

表4 UO2和Zr-UO2中Xe的溶解能,ΔEs表示Zr掺杂后Xe的溶解能的变化量(eV)Table 4.Solution energies of Xe in UO2and Zr-UO2,ΔEsrepresents the solution energy variation of Xe after Zr doping(eV).

4 结 论

本文在U富集和O富集的情况下,研究了Zr掺杂到UO2中所引起的空位缺陷形成能力的变化.虽然两种情况下空位缺陷的形成能力不同,O富集时空位缺陷更容易形成,但Zr的掺杂会使两种情况下缺陷的形成能有相同的增加.对Xe吸附到空位缺陷所需的结合能进行了研究,Zr的掺杂会改变结合能的大小,对于所有研究的体系,仅Xe吸附到由4个点缺陷构成的团簇中所需的结合能有所增加,其余情况下的结合能都有一定的减小.计算发现UO2中Zr掺杂后Xe的溶解能增加了,Zr的存在主要通过阻碍空位缺陷的形成而减弱了Xe在UO2中的溶解能力.这对研究反应堆中少量Zr进入燃料UO2中后裂变产物Xe在其中的溶解具有一定指导意义.

[1]Wang H,Yin C G,Liu J H 2013J.Alloys Compd.579 305

[2]Song J H,Park I K,Shin Y S,Kim J H,Hong S W,Min B T,Kim H D 2003Nucl.Eng.Des.222 1

[3]Lei Y L,Huang H W,Yu C,Yang J,Liu Y J 2014J.Mater.Sci.Eng.32 126(in Chinese)[雷艳丽,黄华伟,喻冲,杨静,刘艳军2014材料科学与工程学报32 126]

[4]Matzke H,Turos A,Linker G 1994Nucl.Instrum.Methods Phys.Res.Sect.B91 294

[5]Brutzel L V,Rarivomanantsoa M 2006J.Nucl.Mater.358 209

[6]Martin G,Garcia P,Brutzel L V,Dorado B,Maillard S 2011Nucl.Instrum.Methods Phys.Res.Sect.B269 1727

[7]Xing Z H,Ying S H 2000Nucl.Power Eng.21 560(in Chinese)[邢忠虎,应诗浩 2000核动力工程 21 560]

[8]Yun Y,Kim H,Kim H,Park K 2008J.Nucl.Mater.378 40

[9]Andersson D A,Uberuaga B P,Nerikar P V,Unal C,Stanek C R 2011Phys.Rev.B84 2989

[10]Andersson A D,Perriot R T,Pastore G,Tonks M R,Cooper M W,Liu X Y,Goyal A,Uberuaga B P,Stanek C R https://www.osti.gov/scitech/biblio/1291258/[2017-8-9]

[11]Kulkarni N K,Krishnan K,Kasar U M,Rakshit S K,Sali S K,Aggarwal S K 2009J.Nucl.Mater.384 81

[12]Yang C,Zhang X 2004Mater.Sci.Eng.A372 287

[13]Lan J H,Wang L,Li S,Yuan L Y,Feng Y X,Sun W,Zhao Y L,Chai Z F,Shi W Q 2013J.Appl.Phys.113 183514

[14]Yu J G,Devanathan R,Weber W J 2009J.Phys.:Condens.Matter21 435401

[15]Grimes R W,Catlow C R A 1991Philos.Trans.Phys.Sci.Eng.335 609

[16]Kresse G,Joubert D 1999Phys.Rev.B59 1758

[17]Kresse G,Furthmüller J 1996Phys.Rev.B54 11169

[18]Perdew J P,Burke K,Ernzerhof M 1996Phys.Rev.Lett.77 3865

[19]Dudarev S L,Botton G A,Savrasov S Y,Humphreys C J,Sutton A P 1998Phys.Rev.B57 1505

[20]Vathonne E,Wiktor J,Freyss M,Jomard G,Bertolus M 2014J.Phys.:Condens.Matter26 325501

[21]Dorado B,Amadon B,Freyss M,Bertolus M 2009Phys.Rev.B79 235125

[22]Dorado B,Jomard G,Freyss M,Bertolus M 2010Phys.Rev.B82 035114

[23]Sinnott S B,Uberuaga B P 2014Am.Ceram.Soc.Bull.93 28

[24]Ngayamhappy R,Krack M,Pautz A 2015J.Phys.:Condens.Matter27 455401

[25]Hong M,Phillpot S R,Lee C W,Nerikar P,Uberuaga B P,Stanek C R,Sinnott S B 2012Phys.Rev.B85 144110