基于纠缠见证的路径纠缠微波检测方法∗

朱浩男 吴德伟 李响 王湘林 苗强 方冠

(空军工程大学信息与导航学院,西安 710077)

1 引 言

近年来,国内外对量子领域的研究和探索取得了丰硕的成果[1−4].量子理论逐步走向成熟,大量理论成果都已经在试验中得以验证,并且部分技术已经能够在工程中得以应用,最具代表性的是我国于2016年8月份成功发射的“墨子”号量子科学实验卫星,用于研究基于纠缠光的量子保密通信技术;量子计算、量子雷达[5,6]等颠覆性技术的研究也在稳步进行中.目前,比光频段频率更低的微波频段受到关注,开展了研究微波频段的量子现象[7−9],并且已经取得了初步的成果,国外一些研究小组已经在实验中产生了空间分离的连续变量纠缠微波信号[10−13],实现了路径纠缠.

最常见的纠缠是光学中的纠缠光子对,属于两体纠缠,常见的有光子数纠缠和光子偏振纠缠.但光频光子在传播过程中受外部环境影响大,而微波信号的波长比光信号长,具有光信号所不具备的绕射能力以及能够在复杂环境下传播距离更远的优势.一个微波光子所具有的能量要远低于光频光子,对单个微波光子的探测要更加困难一些,通常对纠缠微波的探测是通过对大量微波光子群叠加形成的电磁场进行测量来完成的.

对于所制备出的两路微波信号,如何验证其处于纠缠态成为一个很重要的问题,本文提出一种基于纠缠见证的纠缠微波信号探测方法,通过构造出探测纠缠态的纠缠见证(entanglement witness)算符[14−16],并应用微波分束器[17]在物理上实现,进行路径纠缠微波的探测.

2 路径纠缠微波简介

2.1 双模压缩微波光子对的纠缠形式

量子纠缠是量子力学中的一种奇特现象,纠缠粒子之间能够表现出非定域的关联性质.路经纠缠微波信号是在微波频段内的量子纠缠,指分布在空间上处于分离状态的两个传播路径上,且能够保持纠缠状态沿着各自的路径传播到信息系统的任意两个部件的纠缠微波场信号,这一现象也可以被认为是微波光子群之间的纠缠.在工程上使用路径纠缠微波就是对微波光子群组成的电磁场的场强测量而非对微波光子的直接探测,这区别于纠缠光的使用.这里对路径纠缠微波进行理论研究和特性分析时,仍然可以在微波光子数态[18]下进行.

制备非经典的微波双模压缩态,其中一种常见方法是使用约瑟夫森参量放大器(Josephson parametric ampli fier,JPA)实现,约瑟夫森参量放大器实现的哈密顿量相互作用可以作为参量下转换哈密顿量,真空态在约瑟夫森参量放大器的作用下产生双模压缩真空态[19].

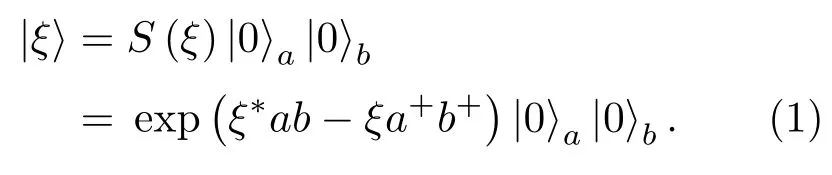
可以定义电磁场模式的正交分量为

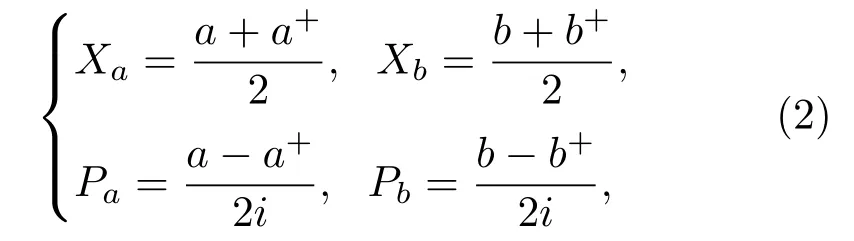
式中Xa,Pa分别代表a模电磁场的正交振幅分量和正交相位分量;Xb,Pb分别代表b模电磁场的正交振幅分量和正交相位分量.

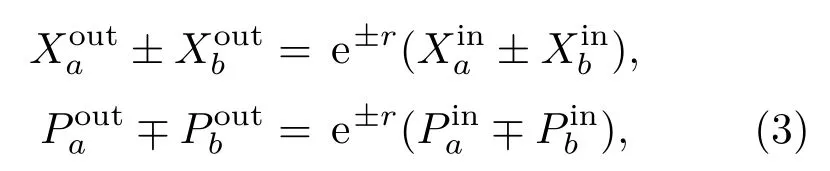
当抽运作用在电磁场和频率为νa+νb时,在约瑟夫森混合器的双模压缩作用下产生a模和b模的双模孪生光子对,这对纠缠微波光子输入输出的正交分量有如下的关系:其中分别代表输入端a模和b模的正交振幅分量;分别代表输入端a模和b模的正交相位分量;分别代表输出端a模和b模的正交振幅分量,分别代表输入端a模和b模的正交相位分量.

由于输入为真空态,因此对上等式两边求二阶期望得到:

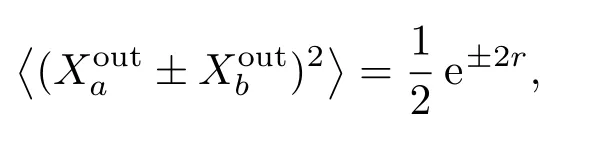
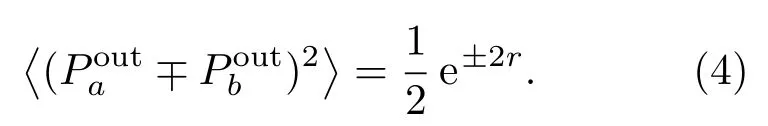
可见输出a,b模的X分量是正相关,P分量是反相关的.由于a,b模微波光子的相位为

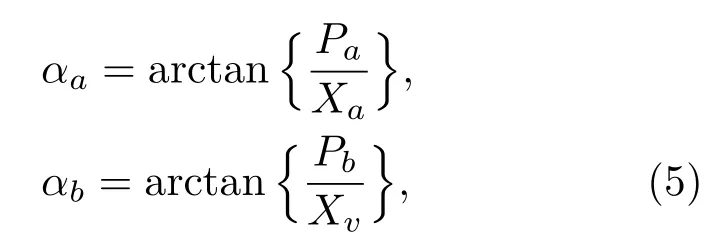
因此也可以认为这对纠缠微波光子的相位是共轭的.

根据上面对双模压缩产生的孪生光子对的分析,双模压缩态产生a模和b模孪生微波光子对有着相互共轭的相位;当单独测量a模光子时它的相位是完全随机的,因此对a模微波光子进行测量会使得其依概率随机塌缩至任意相位,则与之纠缠的b模微波光子会同时塌缩到共轭的相位,使得正交分量的测量结果在X分量是正关联,P分量是反关联的.并且,这种相位上的纠缠属于连续变量纠缠,可以表述为

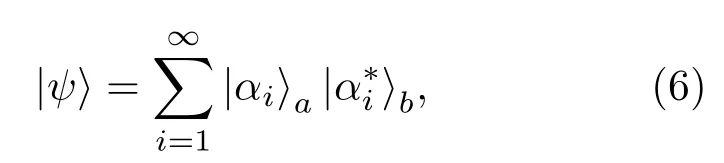
对大量的微波光子构成的电磁场来说,由于场强是大量光子矢量的叠加,虽然对于大量a或b模光子,由于随机起伏的正交分量是矢量线性叠加的,导致它们正交分量幅度出现随机的变化,但a,b模光子群正交分量的关联性不变,起伏几乎完全一致,使得总体的电磁场的X分量正相关,P分量反相关.

2.2 路径纠缠微波的制备方式

路径纠缠微波的制备方式目前有利用约瑟夫森参量转换器的制备方案、利用微波频段HOM效应的制备方案、利用威尔金森功分器的制备方案、利用约瑟夫森参量转换器的制备方案和利用超导180°混合环的制备方案等.制备路径纠缠微波的关键就是制备压缩态的微波信号和用微波分束器对压缩态微波中的微波纠缠光子对进行分离.上面提到的超导180°混合环、威尔金森功分器，基于约瑟夫森结的约瑟夫森混合器等[17]均可作为制备路径纠缠微波的微波分束器.

下面以采用超导180°混合环制备纠缠微波方案为例，对使用微波分束器分离纠缠光子对来制备路径纠缠微波的方法进行简单介绍。如图1所示，约瑟夫森参量放大器产生的压缩态信号[20]和50 Ω负载产生的热态作为超导180°混合环的两路输入信号，超导180°混合环有四个端口，其中两个为输入端，两个为输出端。两路输入信号分别从输入端口进入混合环，在其内部产生干涉效应[21]，通过调节超导环周长，使两路输入信号在端口A,C处产生相消干涉，而端口B,D处产生相长干涉，进而在两个输出端口得到两路路径纠缠微波信号[17]，其输入输出关系为：

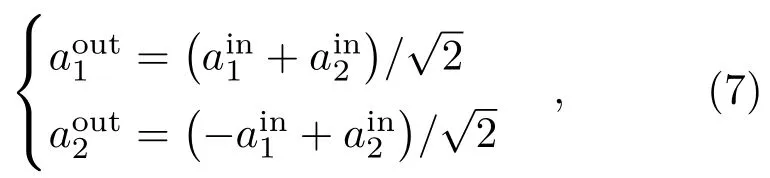
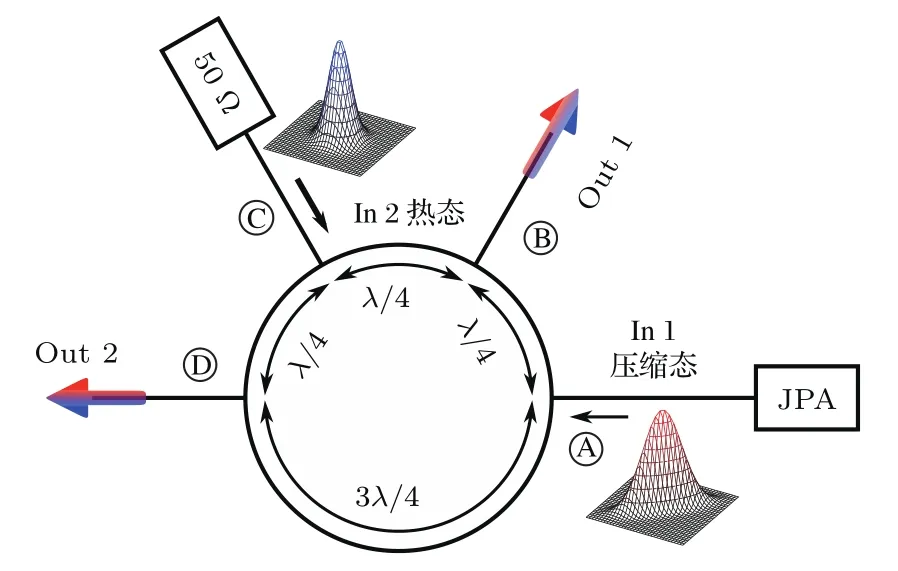
图1 超导180°混合环产生路径纠缠微波示意图Fig.1.Schematic diagram of using superconducting 180 degree hybrid ring to generate path-entangled microwave signals.

3 两种常见纠缠形式纠缠见证的构造

在制备出路径纠缠微波以后,要验证所得到的两路信号是否为纠缠态成为一个关键的问题,这显然是对两体纠缠的探测.已有的纠缠探测判据中,比较著名的有纠缠见证[14]和部分转置正定(positive partial transpose,PPT)判据[22].

纠缠见证是一种可以在物理上直观实现的纠缠探测方式,纠缠见证算符W满足以下三个条件:1)至少有一个负本征值;2)对所有纯直积态都具有非负期望值;3)Tr(W)=1.假如量子态ρAB是可分态,那么它具有非负平均值Tr[WρAB]≥0;假若量子态ρ为纠缠态,其可以被W探测,得到Tr[WρAB]＜0.

PPT判据由Asher Peres于1996年提出,对于一个包含两个子系统的量子系统ρAB,若对其中一个子系统做部分转置后得到的矩阵仍然是一个密度矩阵,即有非负本征值,则这个量子态为可分态;而对于纠缠态,对其中一个子系统做部分转置后得到的矩阵是非正定的,有负本征值.

下面将根据PPT判据,分别对常见的两种2⊗2纠缠进行纠缠见证算符的构造,并给出它们对应的纠缠见证算符形式.

3.1 |ψ〉=A|01〉+B|10〉形纠缠见证算符的构造

下面将结合PPT判据来构造2⊗2量子态的纠缠见证算符,据此探测两路信号是否纠缠.一种常见的两比特纠缠态为

其中|ψ〉=A|01〉+B|10〉,A,B为复系数即概率幅,且|A|2+|B|2=1.

此量子态是部分转置非正定的,是一个纠缠态.因此密度矩阵的部分转置ρT⊗I就有负的本征值,并且设其对应的归一化本征态为|e−〉,即

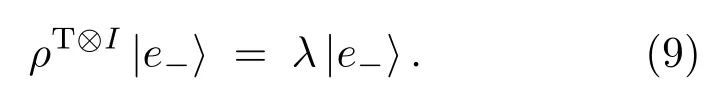
因此有

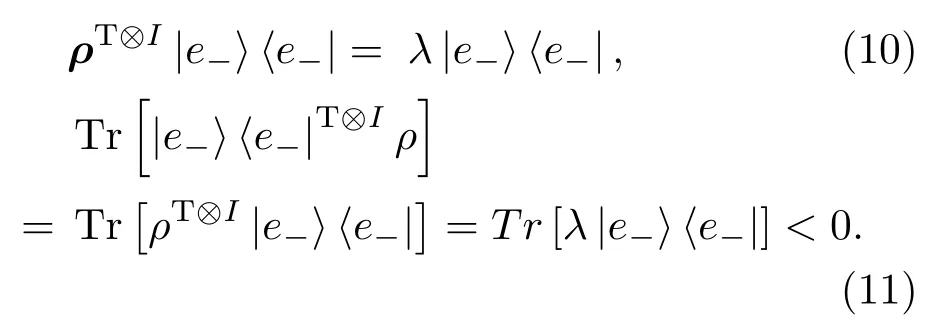
由纠缠见证算符的定义,显然|e−〉〈e−|T⊗I可作为纠缠态ρ=|ψ〉〈ψ|的纠缠见证,纠缠见证算符W为

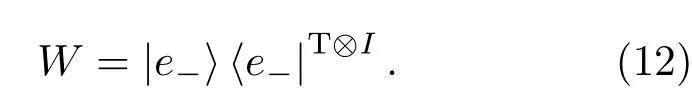
在上述过程中,我们可以得到:

由此得到负本征值对应的本征态为

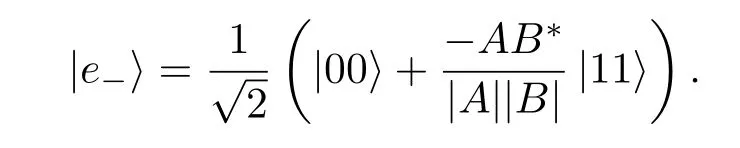
设在上述纠缠态中,系数A,B的相位差为φ,因此W的形式如下:

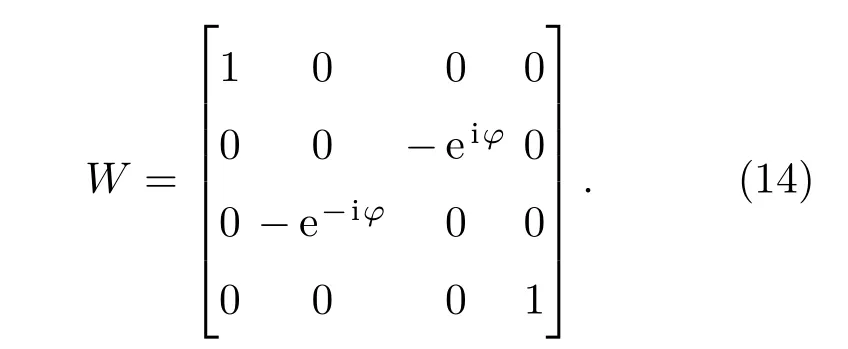
我们发现,若上述相位差φ=π时,即系数A,B反相时,纠缠见证算符W就等效于一个厄米交换(SWAP)算符V,其表述如下:

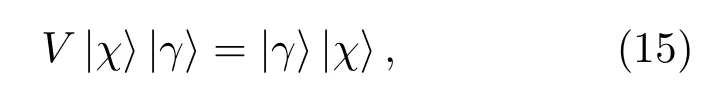
其中|x〉,|γ〉分别表示两个量子态.

3.2 |ψ〉=A|00〉+B|11〉形纠缠见证算符的构造

对于另一种常见的两比特纠缠态为

其中|ψ〉=A|00〉+B|11〉,且|A|2+|B|2=1. 其部分转置矩阵ρT⊗I矩阵为

可以得到负本征值对应的本征态为

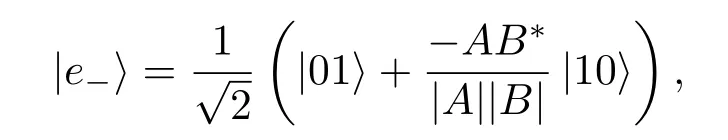
同样的上述纠缠态中,当系数A,B的相位差ϕ=π时,因此纠缠见证W′的形式如下:

综上,两种不同纠缠态纠缠见证算符是有所差异的,同时彼此之间也有一定的联系,第一种纠缠态的纠缠见证W可以用一个受控SWAP门[23]来实现,在受控SWAP门之前再添加一个量子门I⊗X,使得I⊗X门和受控SWAP门的串联线路等效于W′作为第二种纠缠态的探测线路,其本质是先将第二种纠缠转化为第一种纠缠形式,然后用受控SWAP门来实现纠缠探测,其线路图如图2所示.

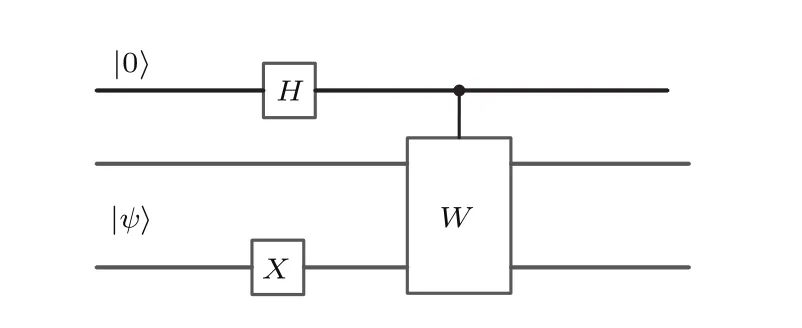
图2 第二种纠缠转化为第一种纠缠的量子线路Fig.2.A quantum circuits to convert the second type entanglement into the fi rst one.

4 应用微波分束器进行路径纠缠微波信号的探测

4.1 路径纠缠微波的纠缠见证

路径纠缠微波的纠缠是属于两体连续变量纠缠,并且纠缠形式为空间分离的纠缠微波光子对相位上的共轭,假如其中一个微波光子塌缩至α相位,那么与之相纠缠的微波光子必然塌缩至相位α∗.由于在制备纠缠微波时,双模压缩真空态的压缩幅度会受到实验设备和外部环境等因素的限制而不会达到无穷大,所以纠缠微波光子对所塌缩的相位并不会完全精确地共轭,而是会有很小的误差.因此实际中所制备纠缠微波的纠缠态维度并不会达到无穷大,可以把它看作是两体多维的纠缠态:

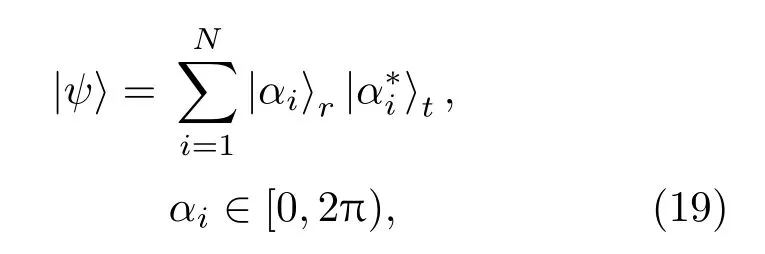
其中r,t分别表示纠缠微波光子对空间分离后传播的两个不同路径;N为纠缠的维度,会受到双模压缩真空态压缩幅度的影响,压缩幅度越大,N也就越大.

接着对路径纠缠微波态做进一步的整理,根据前面的讨论,单独一路中路径微波光子的相位为α∈[0,2π),令相位βi=α∗i,则路径纠缠微波的纠缠形式可以重新表述为

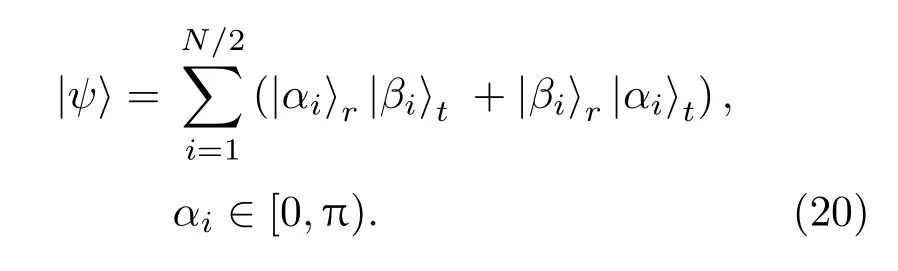
通过上式的表述,利用共轭相位的对称性可以将微波纠缠态分解为无限维的(|01〉+|10〉)形2⊗2纠缠的叠加态.(|01〉+|10〉)形纠缠的纠缠见证算符为:

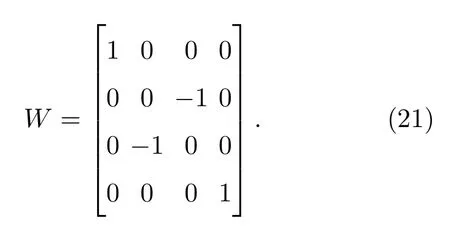
因此上述纠缠见证算符也能够作为大量(|01〉+|10〉)形纠缠叠加构成的路径纠缠微波地探测.

4.2 应用微波分束器构造纠缠见证

使用微波分束器作为干涉仪构造SWAP门,可以实现上述的纠缠探测方法,此方法能够在物理上进行直观观察.微波分束器不仅可以用来进行路径纠缠微波的制备,同样可以用来进行路径纠缠微波的探测和验证.其主要的过程为将两路纠缠的微波信号通过两个端口送入微波分束器后,然后对两个输出端口进行微波光子符合计数,通过符合计数率来观察两路信号是否纠缠.

下面在微波光子数态表象下进行理论上的推导,介绍利用微波分束器构造纠缠见证算符的具体过程.

1)首先将两路量子态微波信号分别从两个入口输入微波分束器,所输入的量子态可以表示为

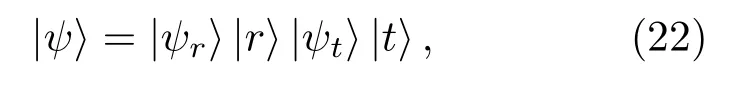
其中r,t分别表示两个输入路径.

2)两路路径纠缠微波信号送入微波分束器后,经过微波分束器的作用,把两个输出信号路径设为u,d,可以得到如下的输出态:

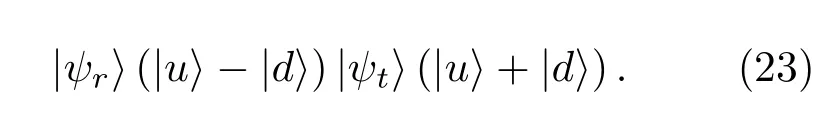
3)接下来对u,d两端口输出的信号进行微波光子的符合计数,符合计数是当两路的计数器同时有光子计数时,进行一次微波光子计数.在这里通过微波光子的符合计数,目的在于去除路径为u,u和d,d部分的信号,即(23)式中

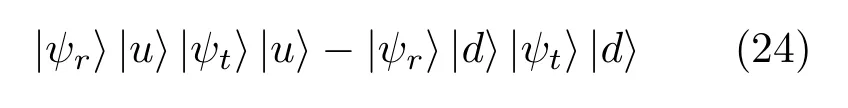
部分,而只留下传输路径为u,d和d,u的信号,得到的量子态为

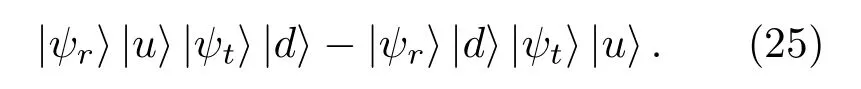
最终得到输出的末态为

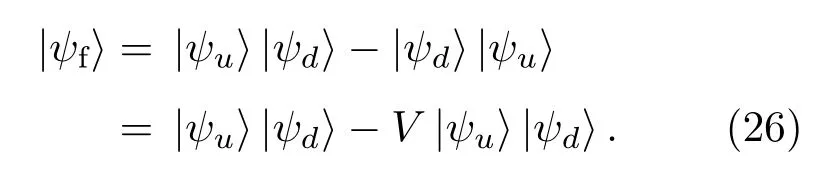
两路信号经过微波分束器和微波光子符合计数的过程,末态中出现了厄米交换算符V.

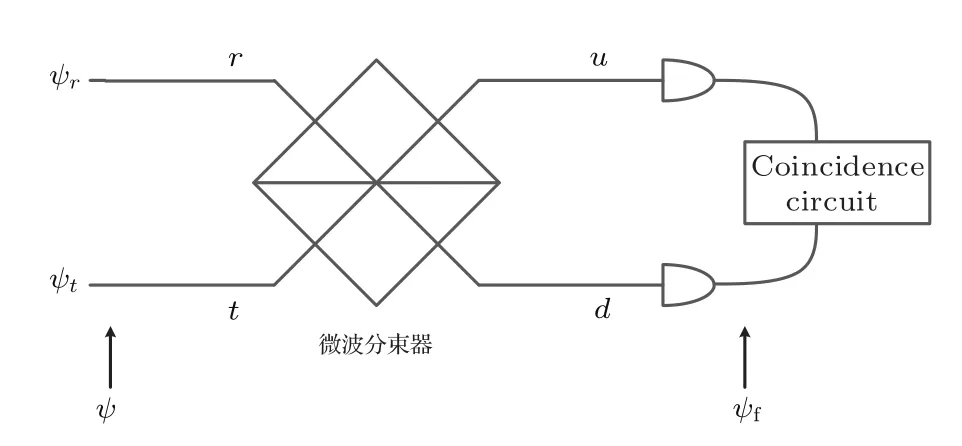
图3 应用微波分束器进行路径纠缠微波检测示意图Fig.3.Schematic diagram of using microwave beam splitter to detect path entangled microwave signals.

接下来对上述末态密度矩阵进一步分析,由于在最后符合计数过程中没有对输出信号进行偏正测量,因此符合计数的结果就正比于末态|ψf〉密度矩阵的迹.末态密度矩阵为

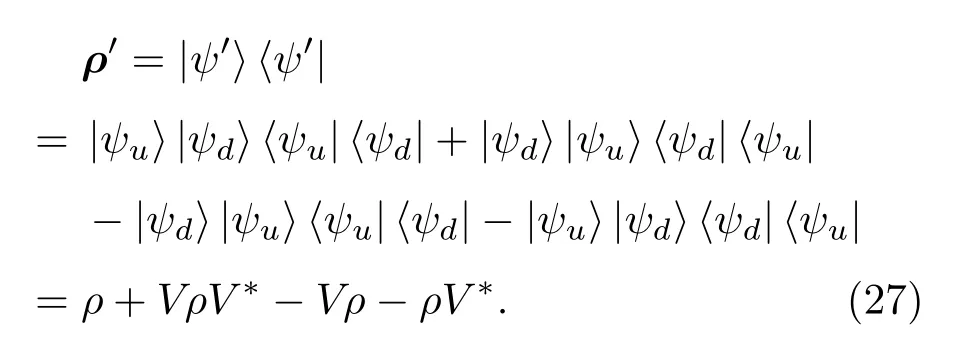
对密度矩阵ρ′求迹可以得到

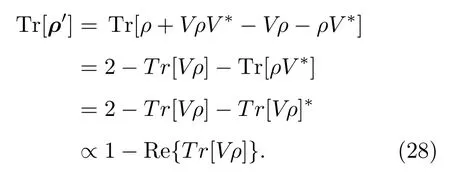
可见通过微波分束器可以得到厄米交换算符V作用在微波量子态密度矩阵上得到Tr[Vρ]的值,而根据前面分析,算符V是(|01〉−|10〉)形纠缠的纠缠见证算符,因此通过微波分束器就能够在物理上实现对此形式纠缠的探测.根据Tr[Vρ]实部的正负可以判断所输入的量子态是否(|01〉−|10〉)形纠缠,能够看出若两路量子态是可分态或不是此类形式的纠缠,则Re{Tr[Vρ]}≥ 0使得Tr[ρ′]小于或等于1;若信号纠缠是这一形式纠缠,则Re{Tr[Vρ]}＜0使得Tr[ρ′]大于1,并且两路信号的纠缠度越大,则Tr[ρ′]越大,导致微波光子的符合计数率越高.直接得到Re{Tr[Vρ]}的正负信息比较困难,可以通过先后输入两路功率相同的纠缠态和标准直积态微波信号,在输出端使用进行微波光子符合计数,通过对微波光子计数率进行对比来判断Re{Tr[Vρ]}的正负,即观察输出端两路是否发生微波光子计数率的翻转,来判别所制备的量子态是否为(|01〉−|10〉)形纠缠态.

在实际的工程中,单个微波光子的能量很弱,导致很难对微波光子进行单光子计数.为了解决这一问题,需要改变对量子态微波的测量方式.我们知道光子的符合计数率正比于二阶关联函数〈Ir(t)It(t)〉, 这里Ir(t),It(t)分别为r,t两路的瞬时光强,瞬时光强又正比于这一时刻场强的平方.这样对同一时刻两路信号场强的平方做互相关,两路信号场强平方的互相关值的大小就正比于两路微波光子的符合计数率的大小.这样就把较为困难的微波光子数测量转化为对场强的测量,减小了处理难度.

目前,已有研究者应用上述类似方法在光学上进行了偏振纠缠态的检测[24];国外研究者通过构造的验证矩阵是否含有负特征值进行了纠缠微波的检测[10].

4.3 路径纠缠微波的纠缠见证的物理实现

在前面的分析中,应用微波分束器可以构造出(|01〉−|10〉)形纠缠的纠缠见证算符V.而路径纠缠微波的纠缠形式为

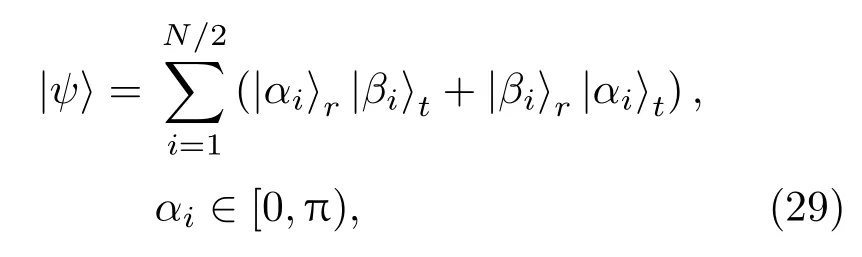
这是N/2个(|01〉+|10〉)形纠缠的叠加,所以微波分束器并不能够直接作为纠缠微波的探测.这就需要其他的量子器件与微波分束器结合起来实现路径纠缠微波的检测,通过观察可以发现,若能够把纠缠微波的纠缠形式变为

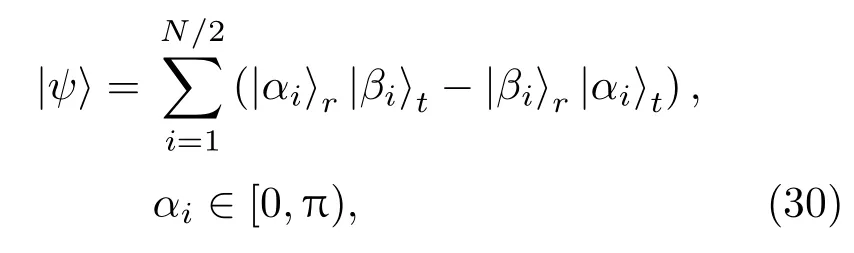
则成为多个(|01〉−|10〉)形二维纠缠的叠加态,这样就能够应用微波分束器来进行纠缠探测了.

实现这一转换过程需要对路径t的微波量子态进行连续变量量子逻辑操作,使t路径微波光子相位在[0,π),即微波光子的Pb分量大于零时,对微波光子进行反相操作,其余情况下不做变化.这个过程可以认为是连续变量的受控相位门,如何在物理上实现这个量子态转换过程目前也有一定的难度,这也有待于实现量子计算的器件进一步发展.综上所述,利用连续变量受控相位门与微波分束器的串联量子线路,就能够在物理上实现路径纠缠微波的探测.

5 总结与展望

本文介绍了利用约瑟夫森混合器制备非经典双模压缩态微波的原理,并通过谐振器或微波分束器将纠缠的光子对分离产生路径纠缠微波的方法.接着结合PPT判据和纠缠见证的定义,推导了两种2⊗2纠缠态的纠缠见证算符的形式.然后将连续变量纠缠的微波纠缠态进行分解,把纠缠微波看作多个2⊗2纠缠叠加的纠缠态,并由此证明利用连续变量受控相位门与微波分束器的组合电路能够在物理上构造路径纠缠微波的纠缠见证算符,用于路径纠缠微波的检测方法,并对试验结果进行了理论上的分析.本文提出的纠缠微波检测方法相比于量子态重构,态估计等纠缠检测方法更加简便直观,一定程度上减少了计算操作,并有更大的容许误差.

[1]Johansson 2012Physics5 103120

[2]Herrmann L G,Portier F,Roche P,Levy Yeyati A,Kontos T,Strunk C 2010Phys.Rev.Lett.104 026801

[3]Recher P,Sukhorakov E V,Loss D 2001Phys.Rev.B63 165314

[4]Ou Z Y,Pereira S F,Kimble H J,Peng K C 1992Phys.Rev.Lett.68 3663

[5]Gisin N,Thew R 2007Nat.Photon.1 165

[6]Zhou C H,Qian W P 2015Radar Sci.Tech.13 457(in Chinese)[周城宏,钱卫平2015雷达科学与技术13 457]

[7]Zagoskin A M,Il’ichev E,McMutcheon M W,Young J F,Nori F 2008Phys.Rev.Lett.101 253602

[8]Eichler C,Bozyigit D,Lang C,Baur M,Steffen L,Fink J M,Filipp S,WallraffA 2011Phys.Rev.Lett.107 113601

[9]Johansson R,Johansson G,Wilson C M,Delsing P,Nori F 2013Phys.Rev.A87 043804

[10]Menzel E P 2013Ph.D.Dissertation(Munich:Technic University of Munich)

[11]Eder P 2012Ph.D.Dissertation(Munich:Technic University of Munich)

[12]Roy A,Jiang L,Stone A D,Devoret M 2015Phys.Rev.Lett.115 150503

[13]Fedorov K G,Zhong L,Pogorzalek S,Eder P,Fischer M,Goetz J,Xie E,Wulschner F,Inomata K,Yamamoto T,Nakamura Y,Di Candia R,Las Heras U,Sanz M,Solano E,Menzel E P,Deppe F,Marx A,Gross R 2016Phys.Rev.Lett.117 020502

[14]Cavalcanti D,Brandao F G S L,Cunha M O T 2005Phys.Rev.A72 040303

[15]Horodecki M,Horodecki P,Horodecki R 1996Phys.Lett.A223 1

[16]Hyllus P,Gühne O,Bruss D,Lewenstein M 2005Phys.Rev.A72 012321

[17]Mariantoni M,Menzel E P,Deppe F,Araque-Caballero M A,Baust A,Niemczyk T,Hoffmann E,Solano E,Marx A,Gross R 2010Phys.Rev.Lett.105 133601

[18]Premaratne S P,Wellstood F C,Palmer B S 2017Nat.Commun.8 14148

[19]Li X,Wu D W,Wang X,Miao Q,Chen K,Yang C Y 2016Acta Phys.Sin.65 114204(in Chinese)[李响, 吴德伟,王希,苗强,陈坤,杨春燕2016物理学报65 114204]

[20]Kim M S,Son W,Buzek V,Knight P L 2002Phys.Rev.A65 032323

[21]Hoffmann E,Deppe F,Niemczyk T,Wirth T,Menzel E P 2010Appl.Phys.Lett.97 222508

[22]Peres A 1996Phys.Rev.Lett.77 1413

[23]Barenco A,Bennett C H,Cleve R,DiVincenzo D P,Margolus N,Shor P,Sleator T,Smolin J,Weinfurter H 1995Phys.Rev.A52 3457

[24]Wang Z W,Li J,Huang Y F,Zhang Y S,Ren X F,Zhang P,Guo G C 2006Phys.Lett.A372 106