基于位相变更的非相干数字全息自适应成像∗
周宏强 万玉红 满天龙
(北京工业大学应用数理学院,北京 100124)
1 引 言
菲涅耳非相干全息(Fresnel incoherent correlation holography,FINCH)作为一种非扫描三维成像技术得到了广泛的关注和研究[1−5].采用准单色的扩展光源(空间非相干光)照明物体,物体上每一物点发出的光通过合适的分光方法,如利用在空间光调制器(spatial light modulator,SLM)加载适当的位相掩膜进行衍射分光[6],分束后的两束光在合适的平面进行自干涉产生点源全息图,所有点源全息图的非相干叠加便是整个物体的全息图.全息图重建过程在计算机实现,经过数值衍射传播后得到重建像.为充分利用光源的时间相干性和系统的空间带宽积,FINCH系统多采用同轴光路配置,结合相移技术[7]实现全息图的记录,在重建过程中去除零级项和孪生像的干扰.FINCH技术作为一种三维显微成像技术[8],经过理论和实验研究已经证明其具有超分辨率成像的特性.结合结构照明或者渐变折射率透镜等方法或元件,实现了FINCH的超分辨率成像[9,10].文献[11]对FINCH成像速度的提高方法进行了研究,通过单通道单次曝光的全息图即可再现出物体的三维信息,加快了记录速度.近年来,在FINCH基础上已发展出基于孔径编码的非相干全息技术(coded aperture correlation holography,COACH)[12,13].
面向实际应用的成像系统不同程度地会受到系统像差的影响,导致系统成像性能下降,成像指标达不到理论预期.基于FINCH技术的显微成像系统中,全息图记录的过程中也会受到某些像差的影响[14,15],造成所记录的全息图含有像差以致于重建像质量不高,分辨率降低.为解决这一问题,Kim[16,17]提出了基于引导星的非相干数字全息自适应光学,该方法先引入一个光轴上的点源作为引导星,记录引导星的多幅相移全息图,得到复值全息图.利用系统引导星复值全息图(点源全息图)的复共轭与扩展物体的复值全息图进行卷积运算,从而实现系统像差的补偿.该方法需要记录引导星和物体的多幅相移全息图,数据量较大,记录速度慢.并且引导星在实际成像系统中的选取往往是非常困难和复杂的,其直径大小、光强度都需要根据实际系统优化.位相变更(phase diversity,PD)是一种有效的基于两幅具有固定位相差异的强度图像计算波前像差的方法[18−21].Klapp和Rosen[15]在FINCH系统中实现了利用PD算法进行波前探测的自适应光学,但其研究工作只给出了简单的模拟结果.
本文进一步发展了基于位相变更的非相干数字全息自适应光学(PD-FINCH),并研究其成像特性.利用全息记录过程中所得到的具有固定位相差的两幅全息图作为初始数据,结合位相变更算法求解出系统像差的位相分布.在本文所提出的方法中,单独提取出光学像差的具体相位分布形式,通过将该相位的共轭加载在光学系统中的空间光调制器上,在全息图记录的同时实现像差校正,从而提高重建像的质量.与传统PD算法中采取的数值校正方法相比,本文提出的方法具有可灵活调制补偿位相、便于分析系统像差模式及像差对成像质量的影响等优势.采用标准分辨率板作为物体进行实验,在系统中存在单一像差和多类别像差的情况下,分别实现了波前像差的探测,经过像差校正后,再现像的质量得到明显的提高.
2 基本原理
菲涅耳非相干关联全息(FINCH)是一种非相干全息成像技术,其全息图记录过程如图1所示.
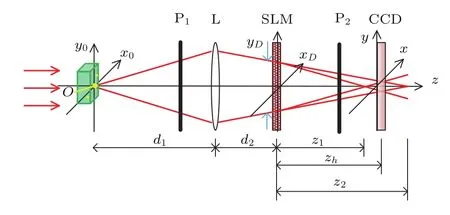
图1 FINCH记录过程示意图Fig.1.FINCH recording principle diagram.
O是扩展型物体在轴上一物点,O到透镜L的距离为d1,透镜L是成像透镜,焦距f1.P1是起偏器,透振方向与x方向成45°角.偏振光束传播到SLM平面,在SLM加载焦距为fSLM的透镜的包裹位相掩膜.根据SLM的偏振敏感特性,只对水平方向偏振的入射光敏感.当入射光偏振方向为45°时,只有入射光的水平分量被调制,而垂直分量没有被调制,且水平分量和垂直分量光强相等.这样一束光经过SLM就被分成两束光,两束光波传播经过P2(检偏器,透振方向与P1平行).至探测器CCD(charge coupled device)平面干涉形成点源全息图.z1,z2分别是物点经过透镜和SLM调制分光后所成的像到SLM的距离.zh为从SLM到CCD的记录距离.
全息图在CCD平面的光强分布可表示为理想的物像与系统点源全息图的卷积,物体的全息图表示为
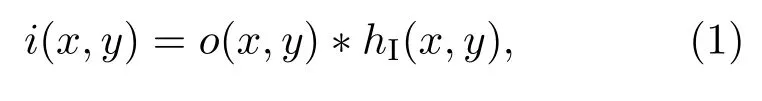
其中o(x,y)是物体的理想像的强度分布,∗代表二维卷积运算,hI(x,y)表示系统的点扩散函数(point spread function,PSF),这里的PSF即为系统点源全息图.
由于FINCH系统为同轴光路配置,在全息图再现过程中,再现像会受到零级项和孪生像的干扰,因此需要结合相移全息技术,去除其对再现像的影响(本文中采用四步相移技术).FINCH中的PSF系统所记录的点源全息图具体形式为

这里Q(1/a)=exp[jπ(x2+y2)/λ/a],λ为光源中心波长;θi代表相移值,i=1,2,3,4,θi分别为0,π/2,π,3π/2.φa为系统像差在SLM面上的位相分布(这里加孔径光阑限定SLM平面为光瞳面),φa由泽尼克多项式前N项的线性组合来描述:
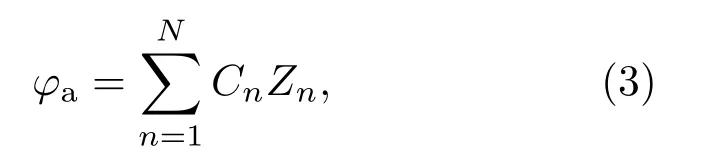
其中,Zn为泽尼克多项式的第n项数学表达式,它和光学像差有直接对应的关系,n=1,2,···,N;Cn表示泽尼克多项式对应第n项的系数,为区别仿真与实验中的参数,仿真中为Cn,实验中为Cen.
在实验设计中,FINCH系统为同轴共路的系统,为精确使用SLM补偿像差,系统设计时,考虑光瞳面限制在SLM平面(图1蓝色箭头处).在SLM上加载透镜位相和像差位相的同时引入一定的相移,记录两幅具有固定相位差的全息图,分别记为i(x,y)和id(x,y).基于PD算法的核心思想,为求得系统的像差,定义评价函数E(o,φa)[22,23]:
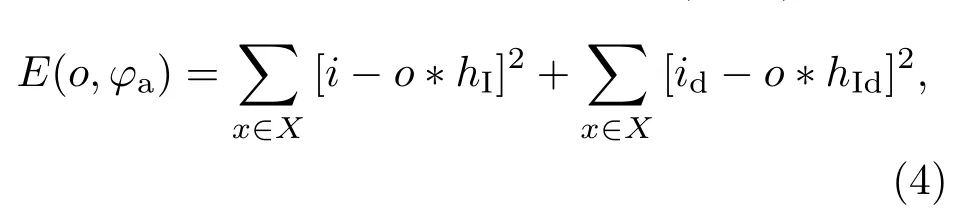
其中hI(x,y),hId(x,y)为成像系统的点扩散函数(PSF),这里分别为FINCH系统的两个点源全息图,分别对应于记录全息图i(x,y)和id(x,y)时的情形.根据Parseval定理和傅里叶变换的性质可知,在频域中,
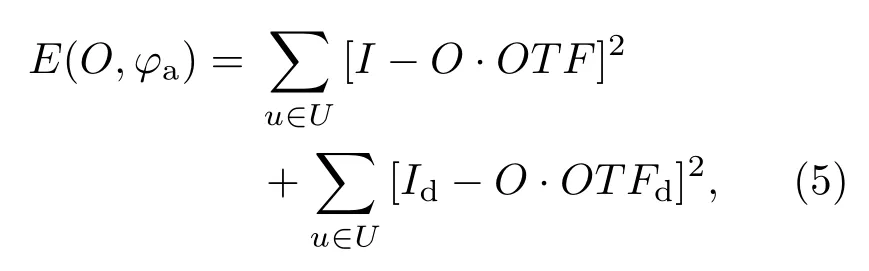
式中I,Id,O,OTF,OTFd分别为i,id,o,hI,hId的傅里叶变换;评价函数E(o,φa)表明通过采集到的两幅具有固定相移差的图像强度分布,可以估算出波前的位相分布(即像差分布).
在目标物体分布函数未知情形下,为了在像差估算过程中使评价函数不受物体分布函数的影响,把函数E(O,φa)对O求偏导,在偏导数为0时,函数取到最小值,此时评价函数的表达式可以写为

(6)式是一个依赖于系统传递函数的一个函数,它并不依赖于物函数.采用遗传算法(genetic algorithm,GA)[24],在不断改变在光瞳面上像差的分布过程中,对上述评价函数的可能解执行大规模并行搜索,找到评价函数的最小值.当某一种像差分布对应于函数取得最小值时,对应的便是最接近实验系统的像差位相.
根据前述理论以及图2的计算过程流程,便可得到计算的像差位相.
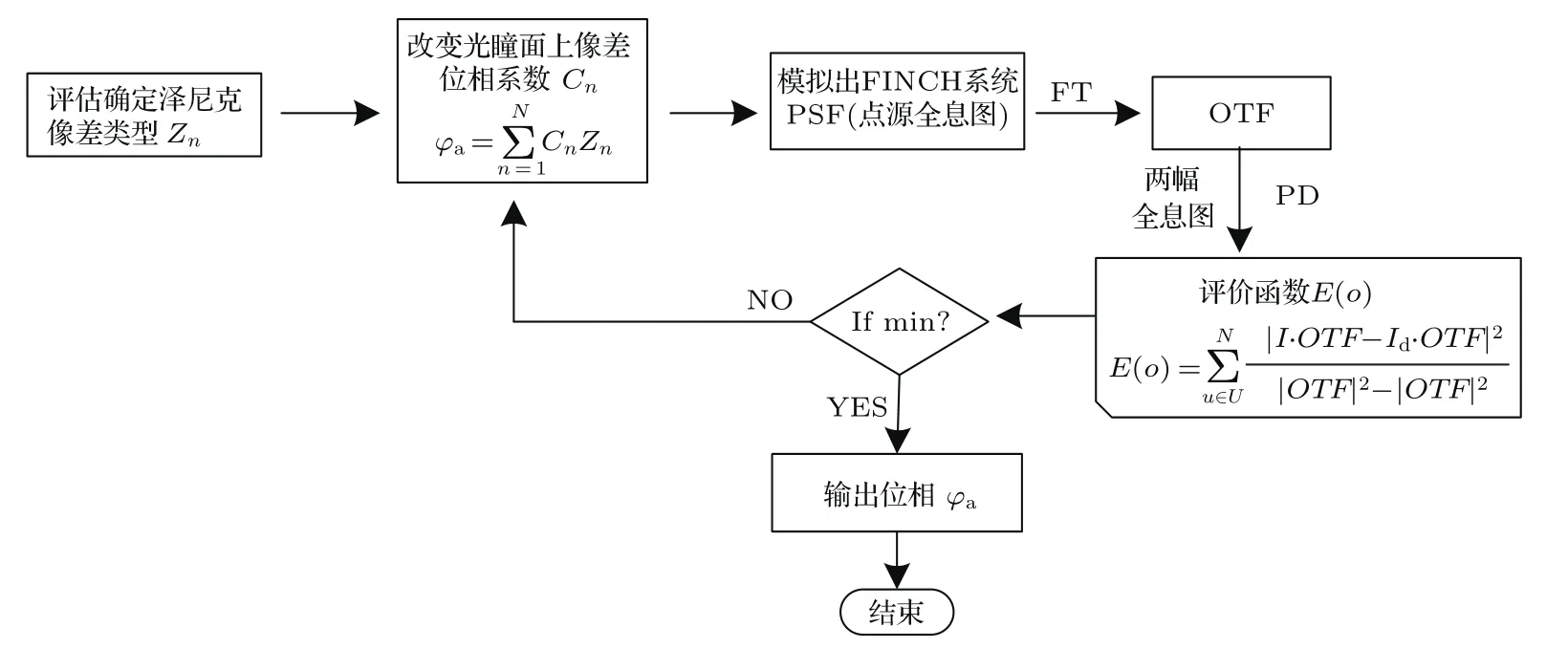
图2 算法流程图(FT表示二维傅里叶变换)Fig.2.Flow chart of algorithm(FT:Fourier transform).
通过上述算法得到像差的位相函数φa后,将φa的复共轭加载到SLM上,结合相移技术记录四幅全息图,合成复值全息图,经衍射传播的一定距离后,可得到经过像差校正的再现像.另外,本文对计算的像差位相和剩余残差用峰谷值(peak-valley value,P-V)和位相标准差(standard deviation,σ)描述和对比校正前后的光瞳面位相的变化程度.
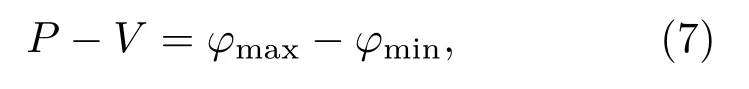
φmax和φmin分别表示光瞳面位相的最大值和最小值;
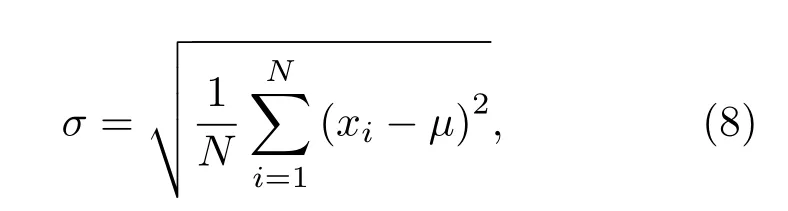
N表示有效光瞳平面区域内像素数,xi表示各个像素值,i=1,2,···N,µ表示所有像素值的平均.
3 仿真与实验
根据图1中的光路结构设计仿真,在FINCH系统中引入彗差,其数学表达式为[25]
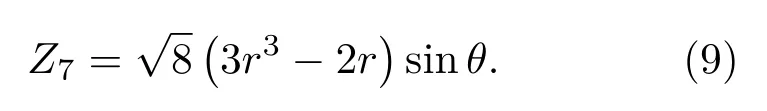
根据(3)和(9)式,使用彗差位相φa=C7×Z7,其系数为C7=0.37作为像差. 极坐标参数非相干光源的中心波长为627 nm,物体到透镜的距离d1=260 mm,透镜L的焦距为f=150 mm,透镜到SLM的距离d2=85 mm;SLM上加载的透镜的焦距为fSLM=−4000 mm,大小为1024×1024像素,每个像素的大小为6.4µm×6.4µm.CCD到SLM的距离zh是279 mm.物光经过起偏后形成与水平方向成45°的线偏振光,衍射传播通过透镜L后照射到SLM上,经过SLM加载的掩膜的调制分光.最后经过检偏器P2使两束光同一偏振态(与P1透振方向平行)后在CCD上干涉产生全息图,改变SLM上的相移间隔,分别记录两幅相移全息图作为PD计算波前像差的强度图.
模拟结果如图3所示,图3(a)为校正前全息图,图3(c)是四步相移全息图的重建像.PD计算后得到的泽尼克彗差系数为C′7=0.371的像差位相.将得到的共轭位相加载到SLM上,补偿系统像差.重新记录四步相移全息图,合成复值全息图,经过角谱传播后得到再现像.图3(b)为补偿像差后记录的全息图.校正后的再现像如图3(d)所示.模拟过程中引入系统的像差位相如图3(e)所示,校正后剩余的像差位相如图3(f)所示.
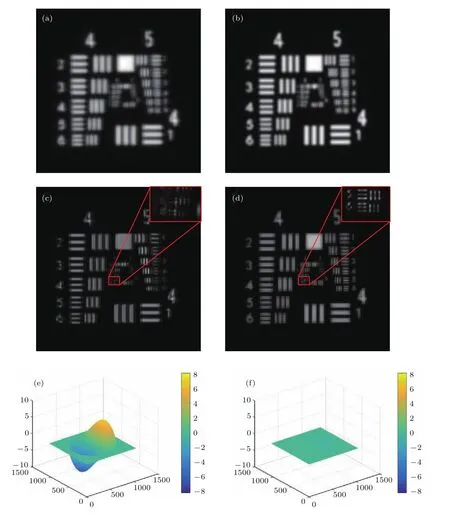
图3 仿真结果 (a)记录的全息图(含有彗差);(b)加载共轭位相补偿像差后记录的全息图;(c)校正前的全息图重建像;(d)校正后全息图重建像(红框中为细节部分放大);(e)模拟中引入的彗差位相(C7=0.37);(f)像差校正后的剩余位相Fig.3.Simulated results:(a)Recorded hologram with coma aberration;(b)recorded hologram after correction coma;(c)reconstructed image with coma;(d)reconstructed image after correction(enlarge the details in the red block);(e)coma aberration phase(C7=0.37);(f)residual phase after correction.
由图3(c)和图3(d)可以看出,经过PD校正后的重建像质量更高,分辨率也提高了.像差位相的P-V由校正前(图3(e))13.06 rad降低到(图3(f))0.035 rad;位相的标准差σ由校正前(图3(e))0.9859 rad降低到(图3(f))0.0027 rad.
为进一步研究所发展的方法的像差校正特性,在系统中引入复杂像差的模式,像散(Z3)、彗差(Z9)、球差(Z12),像差系数为C3=0.4,C9=0.2,C12=−0.3,泽尼克多项式数学表达式如下[25]:

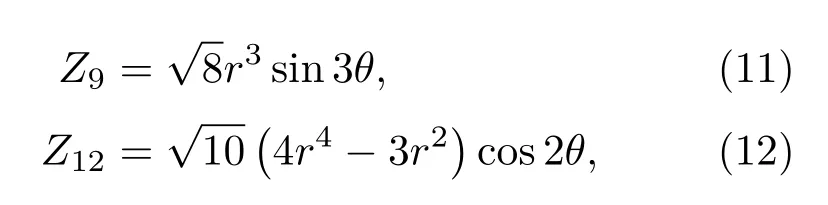
即加入像差位相φa=C3×Z3+C9×Z9+C12×Z12.记录的全息图如图4(a),经过PD计算之后的解为C′3=0.457,C′9=0.18,C′12=−0.284.将其共轭位相加载到SLM上补偿系统像差后记录全息图如图4(b).全息图校正前和校正后的再现像分别如图4(c)和图4(d)所示.模拟过程中,引入系统的像差如图4(e),校正后剩余的像差位相如图4(f).
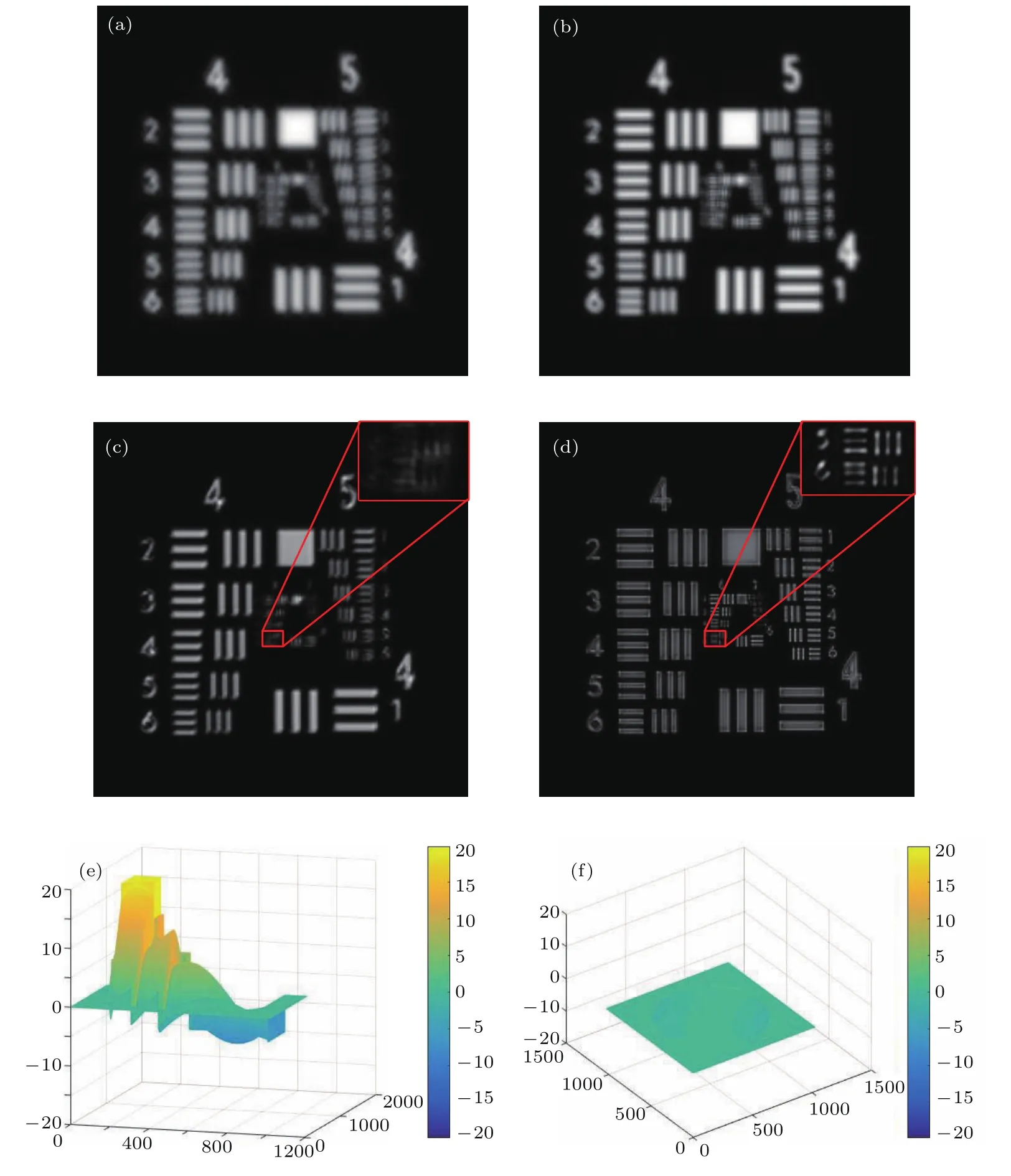
图4 模拟结果 (a)记录的全息图(含有像差);(b)加载共轭位相补偿像差后记录的全息图;(c)校正前的全息图重建像;(d)校正后全息图重建像(红框中为细节部分放大);(e)模拟的像差位相(像散C3=0.4,彗差C9=0.2,高阶球差C12=−0.3);(f)校正后的剩余位相Fig.4.Simulation results:(a)Hologram with aberrations;(b)hologram after aberrations correction;(c)reconstructed image with aberrations;(d)reconstructed image after correction(enlarge the details in the red block);(e)simulated aberration phase(astigmatism C3=0.4,coma aberration C9=0.2,spherical aberration C12=−0.3);(f)the residual phase.
综上模拟结果分析,经过PD校正后,重建像的分辨率得到明显的提高,能看到第6组第6线对(图4(d)).像差位相的峰谷值P-V由校正前(图4(e))26.93 rad降低到(图4(f))2.12 rad;位相的标准差(standard deviation,σ)由校正前(图4(e))2.230 rad降低到(图4(f))0.146 rad.
根据基本理论,设计实验光路如图5所示.
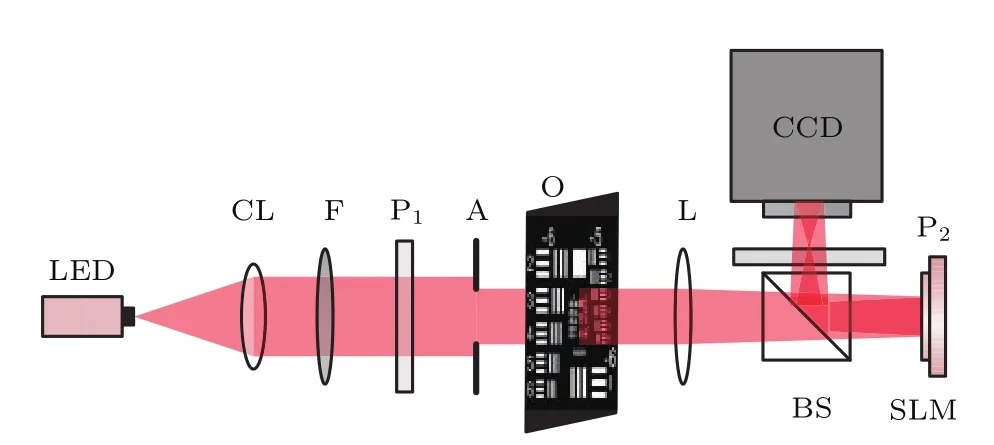
图5 实验光路配置Fig.5.Experimental set-up.

图6 实验结果 (a)记录的全息图(含有彗差);(b)补偿像差后记录的全息图;(c)校正前的重建像;(d)校正后的重建像(红框中为细节部分放大);(e)光瞳面彗差位相(Ce7=0.37);(f)校正后像差的剩余位相Fig.6.Experimental results:(a)recorded hologram with coma aberration;(b)recorded hologram after correction coma;(c)reconstructed image with coma(enlarge the details in the red block);(d)reconstructed image after correction;(e)coma aberration phase(Ce7=0.37);(f)residual phase after correction.
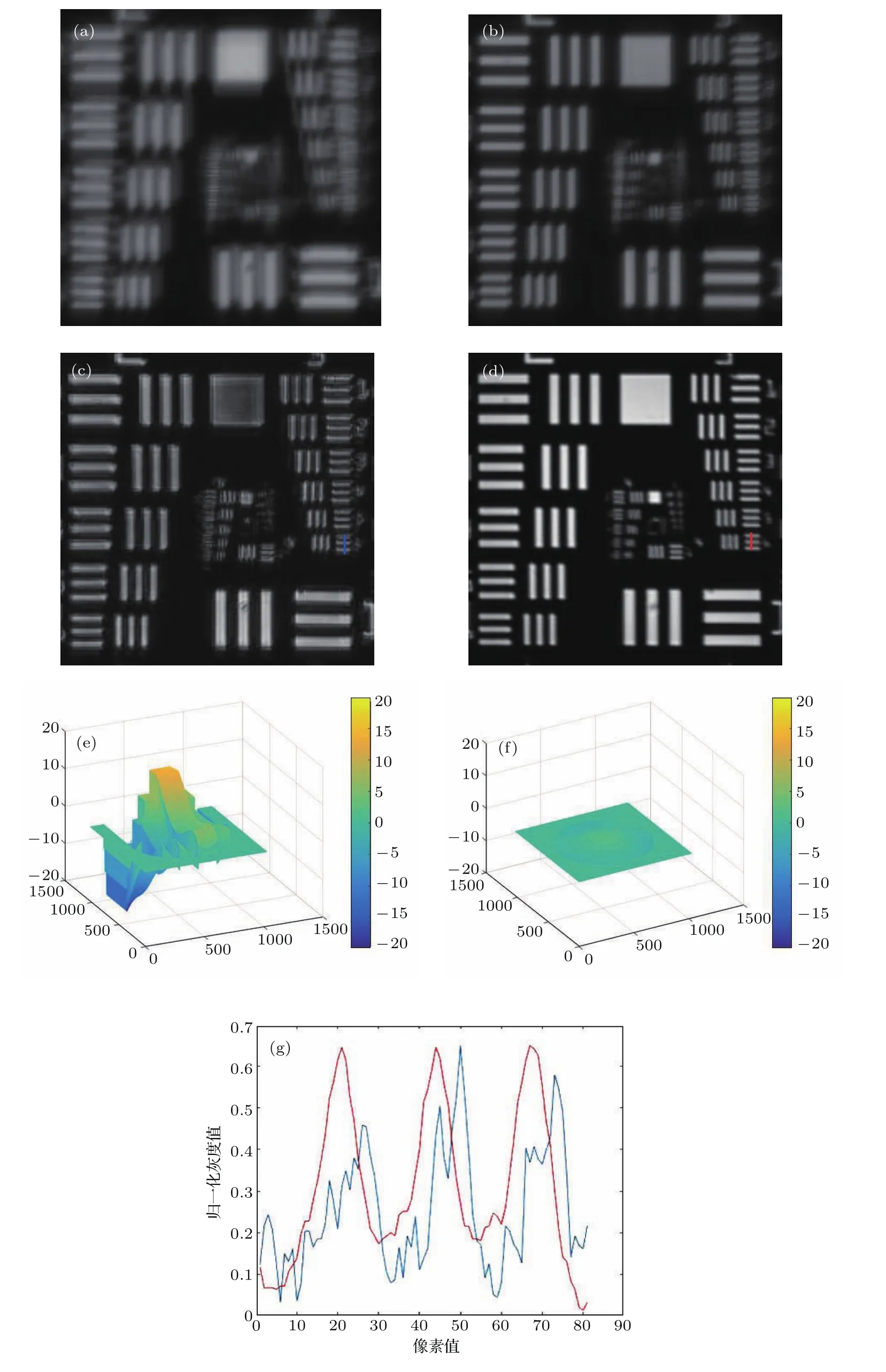
图7 实验结果 (a)记录的全息图含有像差;(b)加载共轭位相补偿像差后记录的全息图;(c)校正前的全息图重建像;(d)校正后全息图重建像;(e)光瞳面像差位相(像散Ce3=−0.3,彗差Ce9=−0.4,高阶球差Ce12=0.2);(f)校正后的剩余位相;(g)归一化校正前(c)和校正后(d)条纹对比度曲线(红线(d);蓝线(c))Fig.7.Experimental results:(a)Hologram with aberrations;(b)hologram after correcting aberrations;(c)reconstructed image with aberrations;(d)reconstructed image after correction(bottom right:normalized fringe contrast curve,the red is after correction);(e)simulated aberration phase(astigmatism Ce3=−0.3,coma aberration Ce9=−0.4,spherical aberration Ce12=0.2);(f)phase distribution of the residual aberration;(g)the normalized contrast curve before and after correction(red(d);blue(c)).
实验系统中,照明光源采用LED,中心波长为627 nm,带宽是16 nm.CL是准直透镜,焦距为75 mm.光束经过准直后起偏器P1后变成线偏振光.将P1的透振方向调节到与水平方向成45°角的方向.A为可变光阑.采用标准分辨率板(USAF 1951)作为物体O,分辨率板到透镜L的距离大约为262 mm.透镜L的焦距为f=150 mm.经过分光棱镜(beam splitter,BS)后照射到空间光调制器(SLM,Holoeye LETO 3.0)上面.SLM像素数为1920×1080,像元尺寸6.4µm×6.4µm.SLM是LCOS纯位相型的反射式空间光调制器.由于该SLM只对水平偏振的入射光敏感,将P1的透振方向旋转至与水平方向呈45°角,此时入射到SLM上的光波的为线偏振,并为与水平方向夹角为45°,光强比近似为1:1只有水平分量的光波前被调制,垂直分量没有被调制.物光经过透镜和SLM调制分光后在CCD平面自干涉产生全息图.CCD与SLM间距为279 mm.其中CCD(Thorlabs DCU224 M,1280×1024)像元尺寸4.65µm×4.65µm.
实验过程中,在SLM平面加载直径为800像素的圆形掩膜作为孔径光阑将系统的光瞳面限制在SLM 平面.并将透镜位相掩膜和像差(彗差系数Ce7=0.37)加载到SLM上,记录四幅相移全息图,组合成复值全息图.经过角谱传播一段距离得到再现像,实验中再现距离为4.5 mm.实验结果如图6所示,其中图6(a)和图6(c)为校正前全息图和重建像.利用记录的前两幅全息图和相移值,经过PD算法计算后,得到的彗差系数为Ce′7=0.36.为补偿系统像差,将得到的共轭位相加载到SLM上,重新记录四幅相移全息图,合成复值全息图,经过角谱传播到指定距离,便可得到清晰的重建像.校正后的全息图和再现像分别如图6(b)和图6(d)所示.同时可以看到系统的彗差像差位相以及补偿后的剩余位相如图6(e)和图6(f).
利用PD算法求解得到系统的泽尼克系数为Ce′7=0.36. 比较图6(c)和图6(d)中校正前后的重建像,红色方框中细节部分可以清楚地看到,校正后的图像质量得到明显的改善,分辨率也有明显的提高.像差位相的峰谷值P-V由校正前(图6(e))13.06 rad降低到(图6(f))0.353 rad; 位相的标准差σ由校正前(图6(e))0.9859 rad降低到(图6(f))0.0266 rad.
在系统中引入复杂像差模式,以研究本文所提出的自适应成像方法对不同像差类型的校正性能.该方法对于泽尼克多项式描述的前12项像差均有校正作用,本文针对荧光显微成像中可能存在对成像质量影响较大的低阶像差(前12项如像散,彗差,球差),模拟和实验都选取了不同的像差模式和不同系数大小进行实验验证,都得到了良好的校正效果.这里展示的是在系统中引入像散(Z3),彗差(Z9),球差(Z12),其中像差系数分别为Ce3=−0.3,Ce9=−0.4,Ce12=0.2.经过实验并计算求解之后的解为Ce′3=−0.29,Ce′9=−0.48,Ce′12=0.28.实验结果如图7所示.其中图7(a)和图7(c)为像差校正前的全息图和重建像,校正后的全息图和再现像如图7(b)和图7(d)所示.同时可以看到系统所引入的像差位相以及补偿后的剩余像差位相如图7(e)和图6(f).图7(g)给出了图7(c)和图7(d)中沿红线标示方向的再现像图像强度分布.
从实验结果上看,校正效果明显,分辨率提高,校正前后的条纹对比度都有明显的提高.像差位相的峰谷值P-V由校正前(图7(e))34.36 rad降低到(图7(f))3.73 rad;位相的标准差σ由校正前(图7(e))2.34 rad降低到(图7(f))0.30 rad.
4 结论与讨论
本文结合位相变更算法发展了一种基于非相干数字全息的自适应光学成像技术(PD-FINCH).所提出的方法仅需利用全息记录过程中所得到的具有固定位相差的两幅全息图即可实现系统像差的探测.并且光学像差的具体相位分布形式被单独提取出来,校正过程采用加载共轭位相到SLM进行灵活补偿,校正过程可分离出系统像差分析,校正效果可定量评价.与基于引导星的非相干数字全息自适应光学的方法相比,该方法记录速度更快,校正补偿方便灵活并且校正效果可以定量地评价.本文通过模拟和实验验证了该方法的可行性,并研究了PD-FINCH系统的自适应成像特性.研究表明,利用所发展的方法,FINCH系统内存在的像差得到了有效校正,成像性能提升,分辨率和校正前后的条纹对比度都有明显的提高.PD-FINCH系统成像性能的提升,将有力推进其在荧光成像系统,三维显微成像领域的应用进展.
[1]Rosen J,Brooker G 2007Opt.Lett.32 912
[2]Man T L,Wan Y H,Wu F,Wang D Y 2017Appl.Opt.56 F91
[3]Wan Y H,Man T L,Wu F,Wang D Y 2014Opt.Express22 8565
[4]]Shi X,Yuan B,Zhu W F,Liang E J,Liu X M,Ma F Y 2014Proceedings of the Holography,Diffractive Optics,and Applications VI9271 92710W
[5]Siegel N,Rosen J,Brooker G 2013Opt.Lett.38 3922
[6]Katz B,Rosen J,Kelner R 2012Opt.Express20 9109
[7]Yamaguchi I,Zhang T 1997Opt.Lett.22 1268
[8]Rosen J,Brooker G 2008Nature Photonics2 190
[9]Kashter Y,Vijayakumar A,Miyamoto Y,Rosen J 2016Opt.Lett.41 1558
[10]Brooker G,Siegel N,Rosen J,Hashimoto N,Kurihara M,Tanabe A 2013Opt.Lett.38 5264
[11]Kelner R,Rosen J 2012Opt.Lett.37 3723
[12]Vijayakumar A,Ashter Y,R Kelner,Rosen J 2016Opt.Express24 12430
[13]Vijayakumar A,Rosen J 2017Opt.Express25 13883
[14]Man T L,Wan Y H,Wang D Y 2015Proceedings of the Holography:Advances and Modern Trends IV9508 950804
[15]Klapp I,Rosen J 2013Proceeding of Imaging and Applied Optics.CTH3C
[16]Kim M K 2012Opt.Lett.37 2694
[17]Kim M K 2013Appl.Opt.52 A117
[18]Gonsalves R A,Chidlaw R 1979Proceedings of the Applications of Digital Image Processing207 32
[19]Gonsalves R A 1982Opt.Engineering21 829
[20]Li F 2012Acta Phys.Sin.61 230203(in Chinese)[李斐2012物理学报61 230203]
[21]Li F,Rao C H 2012Acta Phys.Sin.61 029502(in Chinese)[李斐,饶长辉 2012物理学报 61 029502]
[22]Paxman R G,Fienup J R 1988J.Opt.Soc.Am.A5 914
[23]Paxman R G,Schulz T J,Fienup J R 1992J.Opt.Soc.Am.A9 1072
[24]Lei Y J,Zhang S W 2014Matlab Genetic Algorithm Toolbox and Applications(2nd Ed.)(Xi’an:Xidian University Press),pp143–182(in Chinese)[雷英杰, 张善文2014 MATLAB遗传算法工具箱及应用(第二版)(西安:西安电子科技大学出版社第143—182页]
[25]Noll R J 1976J.Opt.Soc.Am.66 207

