基于实数全息图的无零级光全息显示技术

杨靖宇

（四川大学，成都 610065）

1 引言

由于零级光占有全息图再现时大部分的光强。消除全息显示系统中的零级光一直都是全息界的热点话题。如果能够设计出无零级光的全息系统，也就能够获得高效率，高亮度的全息图。

2 计算全息术滤波的局限

计算全息中的数字滤波技术能够同时消除零级光和共轭光，在计算机上生成只含有正1级光（目标图像）的再现结果。然而，这样滤波得到的频谱如果变换回全息图得到的是复数型全息图。由于缺乏显示复数型全息图的空间光调制器，这样的数字全息系统是无法搭建的。相比之下，实数型全息图则更有潜力。

3 实数全息图

将全息图的频谱域的-1级光和0级光滤去。得到的新频谱逆傅里叶变换回全息图。取新全息图的实部得到有正负取值的全息图。

式中，IH指原全息图；F（）为傅里叶变换；P0为滤波函数；F-1为逆傅里叶变换；Re为取实部。采用离轴全息，以四川大学校徽为例，在MATLAB上制作出实数全息图。程序如附录所示。首先，用fft2（快速傅里叶变换）计算原始图像的菲涅尔衍射。这里采用的计算方法是[1]中提到的S-FFT算法。然后设置一个与物光传播方向有恰当夹角的参考光，计算物光与参考光的干涉。将干涉的复数结果取振幅得到全息图。再用快速傅里叶变换计算该透过率为正实数的全息图的频谱。将频谱-1级和0级所在的位置取为0。然后逆傅里叶变换得到一个复数全息图，取复数全息图的实部得到实数全息图。

图1 原始图像

图2 滤波前全息图

其中归一化频谱＞1/10部分皆显示为白色，滤波操作滤去了左上角的-1级频谱和中央的0级频谱。如图6所示，用bar3函数展示了100个像素点的全息图。由于滤波后取实部的全息图有正负取值，因此用imshow（）无法体现全息图的正负性，在这里使用bar3函数，bar3绘图在1024*1024像素的情况下会给计算机很大的负担，因此只取其中10000个像素显示。

图3 滤波前全息图再现结果

图4 滤波前频谱

图5 滤波后频谱

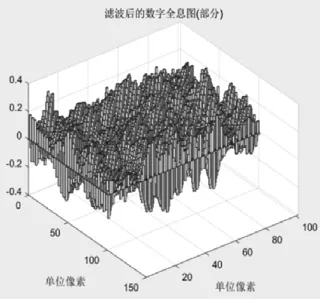
图6 滤波后取实部的全息图

图7 实数全息图的再现像

IH′作为有正负取值的实数全息图，其正负取值刚好使得通过其的光场在光线传播方向（0级光方向）完全干涉相消。如果将这样的实数全息图变换到频域可以看到其频域只含有右下和左上的点。这刚好对应了±1级像。

4 显示实数全息图的空间光调制器

数字全息显示系统中，数字微镜器件DMD（Digital Micromirror Device）是最常用的空间光调制器。DMD利用反射镜面的翻转来实现光开关的“开”、“关”状态。再通过PWM波控制开关速率，快速开闭的反射镜面利用人眼的视觉暂留产生灰度图像。

图8 数字微镜器件

如图8所示，为了实现反射镜面的受控翻转，数字微镜阵列包含了3个部分-电路部分，机械部分，以及光学部分。其正常工作时，最下层的数字微镜单元电路产生驱动信号，驱动信号使得中间层的机械部分运转，带动铰链翻转最上层的反射镜面。然而，这样的数字微镜阵列仅能实现正实数透过率的全息图。对于有正负取值的实数全息图，由eiπ=-1，要实现负值则需使得光线产生π的相位差。

产生π相位差有如下几个方法：

（1）制作新型空间光调制器。如果能够在DMD的机械部分增加一个前后推动的微细推手，使得该推手接收驱动信号后将其前方的反射镜面向前推移1/4个波长，经反射后也就与其他位置的光产生了·2=π的位相差了。

（2）利用半波损失。当光从折射率小的光疏介质射向折射率大的光密介质时，反射光相对于入射光有π的位相突变。如果将两个DMD互成一定角度，其中一个DMD为主DMD，激光源发射的光入射到该DMD后反射到±12°的方向。±12°为观察方向，-12°方向设置另一个DMD，其距离主DMD整数个波长，调整其在水平面的角度，使得其反射到-12°方向的光刚好投射到屏上，与原DMD的±12°光发生干涉，-12°光因为2次反射而与±12°拥有π的位相差，从而干涉相消，消除掉0级光。

（3）利用相位型衍射光学元件。如果在DMD表面放置一个二元相位型的衍射光学元件。该二元衍射元件阶梯高度为也能产生π的相位差。该相位型衍射光学元件可由普通光刻机简单地制作出来，对光刻精度要求很小，但仅限于静态全息。title（‘物平面重建图像'）；axis square。